FLD1_HW001 תרגיל בית 1

	סטודנט א’
שם	עידו פנג בנטוב
ת”ז	CLASSIFIED
דואר אלקטרוני	CLASSIFIED

שאלה 1

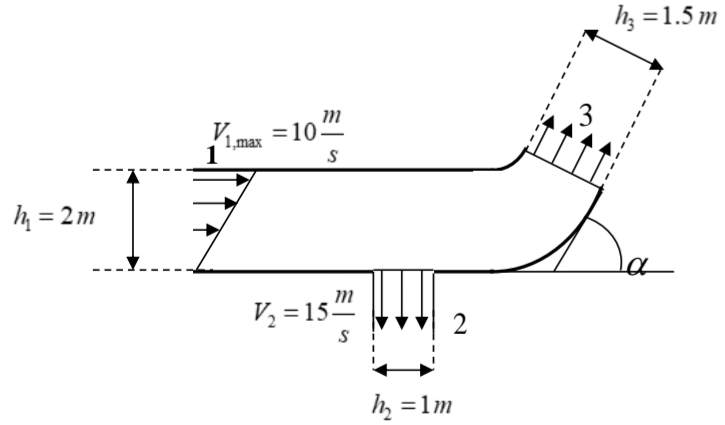
נבחר את נפח הבקרה שלנו כהתעלה. לפי חוק שימור המסה האינטגרלי:

נפח הבקרה קבוע עם הזמן, ו- אחיד, כך שהביטוי הראשון מתאפס. נמשיך לפתח:

נציב נתונים ונקבל:

נשים לב שהתוצאה לא תלויה ב-.

שאלה 2

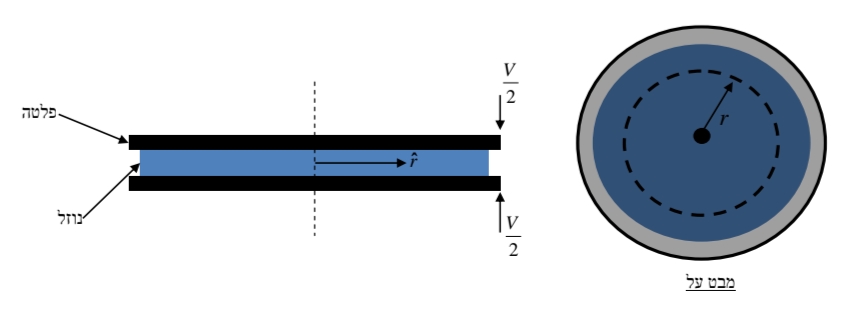
נשתמש בקואורדינטות גליליות - .

סעיף א’

נבחר כנפח בקרה את הנפח בין שתי הפלטות. לפיכך, נפח הבקרה שלנו משתנה עם הזמן.

בחירת נפח הבקרה. נשים לב כי המרחק בין שתי הפלטות הוא . בנוסף, מהירות כל פלטה היא . תודה רבה לניסוח המעולה של השאלה s/.

לפי חוק שימור המסה:

הצפיפות אחידה, כך שנוכל לחלק את כל המשוואה בה:

נגדיר את המהירות ביציאה בכיוון החיובי של :

נציב בחזרה, כאשר נשים לב שהשטח של היציאה תלוי במיקום הפלטה העליונה שנסמן ב-, ומיקום הפלטה העליונה, שנגדי לפלטה העליונה ():

מנתוני השאלה:

הנפח ההתחלתי הוא . כאשר הוא מתחיל להתכווץ:

נגזור לפי :

נציב בחזרה בשימור מסה:

סעיף ב’

נבחר את הנפח בקרה שלנו כהנפח בין הפלטות בזמן כללי. כלומר, נפח הבקרה שלנו קבוע עם הזמן. נוכל לחשוב על החלק העליון והחלק התחתון של הנפח בקרה ככניסה של נוזל.

בחירת נפח הבקרה.

לפי שימור מסה:

נפח הבקרה קבוע, וגם אחיד:

המהירות בכניסות (שתי דסקות, במהירות כל אחת):

נגדיר את המהירות ביציאה בכיוון החיובי של :

נציב:

כמו בסעיף קודם:

נציב ונקבל:

שאלה 3

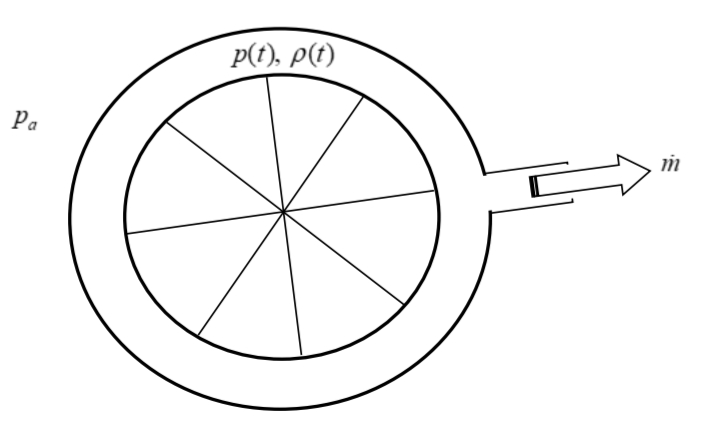
נבחר כנפח בקרה את הצמיג. משימור מסה:

נשים לב הצפיפות אחידה עם הנפח כך שנוכל להוציא אותה מהאינטגרל. בנוסף, הביטוי הימני הוא למעשה הספיקה :

נתון גם כי:

לכן, קיים כך ש:

נציב בביטוי לשימור מסה:

מהגדרת הצפיפות, והנתונים, מתקיים . לפי גזים אידיאליים, . לכן:

נציב בביטוי לשימור מסה:

נבצע פירוק לשברים חלקיים:

נתון ש- , ולכן:

נציב:

נתון גם כי . נחזור לתחילת המד”ר (נציב במד”ר):

נציב בביטוי ל-:

שאלה 4

סעיף א’

נמצא את הקו מסלול. עבור :

נציב תנאי התחלה:

ולכן:

עבור :

לאחר הצבת תנאי התחלה:

קיבלנו את העקומה:

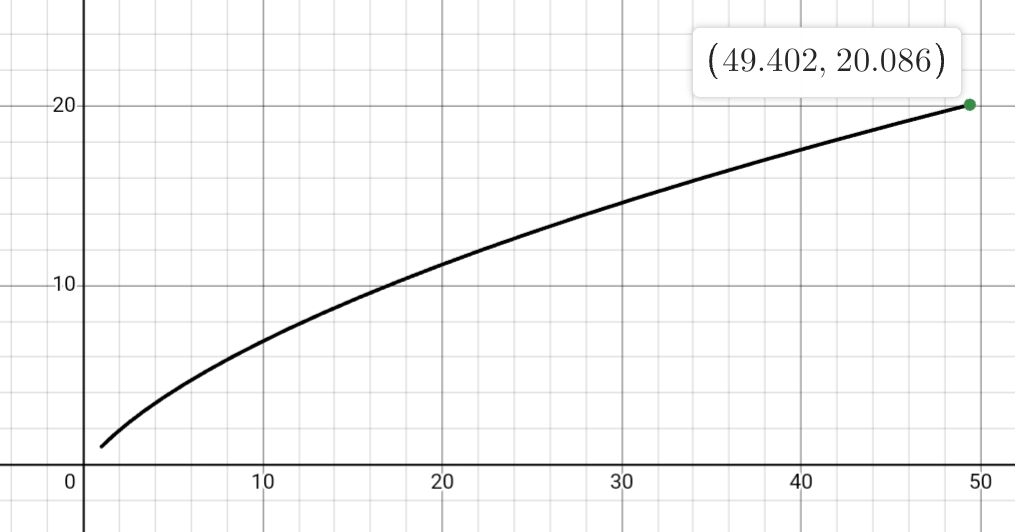
העקומה .

סעיף ב’

נגזור את רכיבי המהירות:

נקבל:

סעיף ג’

בדו ממד אנו יודעים ש:

נציב את שדה המהירות:

נציב את ונקבל: