| סטודנט א’ | סטודנט ב’ | |
|---|---|---|
| שם | עידו פנג בנטוב | הדס כץ |
| ת”ז | CLASSIFIED | CLASSIFIED |
| דואר אלקטרוני | CLASSIFIED | CLASSIFIED |
| תאריכי ביצוע המעבדה | 29/04/2025 | 06/05/2025 |
|---|---|---|
| תאריך הגשה | 28/04/2025 |
הדוח/פרויקט המוגש בזאת הוא פרי של עבודה וחשיבה עצמאית שביצענו עם חברי הקבוצה בלבד. אנו מצהירים שנעזרנו באחד או יותר מהאמצעים שהוזכרו באופן הבא:
- צ’אט GPT - עזרה בניסוח בלבד.
רקע מדעי
ריכוז מאמצים
ריכוז מאמצים מתאר אזור שבו הכוח הפועל על הדגם יוצר מאמץ גבוה מהרגיל, לרוב עקב הפחתה מקומית בשטח החתך (כגון חור, סדק או חריץ). לתופעה זו חשיבות מכרעת מאחר שכשל מכני לרוב נוטה להתחיל מאותו אזור.
מקדם ריכוז המאמצים מוגדר כיחס בין המאמץ המקסימלי
במקרה של ריכוז מאמצים הנגרם עקב חור עגול ברדיוס בפלטה הנתונה למתיחה, קיים פתרון אנליטי של Kirsch לחישוב מקדם ריכוז המאמצים, תחת ההנחות הבאות:
- הפלטה דקה ובעלת ממדים אינסופיים במישור.
- החומר מתנהג בצורה אלסטית (כולל באזור של המאמץ המקסימלי).
בהתבסס על (Kirsch, 1898), התפלגות המאמץ המשיקי בקואורדינטות קוטביות מתוארת על ידי:
כאשר:
לפי פתרון זה, הערך המקסימלי של
התפלגות מרחבית של עיוותים פלסטיים
כאשר מתרחשת פלסטיות, העיוותים אינם מתפלגים בצורה אחידה אלא מתרכזים באזור צר שבו מופיעים עיוותי גזירה גבוהים במיוחד. תופעה זו מובילה להיווצרות צוואר, הופעת נקבוביות ולבסוף לכשל.
מקדם עוצמת מאמצים בקצה סדק
בתורת השבר, מאמצים ליד קצה סדק באלסטיות לינארית שואפים לאינסוף. לכן במקום לדבר על ריכוז מאמצים, משתמשים במושג מקדם עוצמת המאמצים (stress intensity factor).
עבור דגם של פלטה דקה שיש בה סדק לאורך ציר
כאשר:
המקדם
כאשר
מטרות המעבדה
- היכרות והתנסות בשתי השיטות הנפוצות ביותר למדידת עיבורים, מדי עיבור (gauge strain) ו- (DIC (correlation image Digital. הדגמה של מיפוי עיבורים באמצעות צילום המבוסס על תופעת הפוטואלסטיות.
- הבנת המאפיינים של כל שיטה במונחים של רזולוציית עיבורים, תחום עיבורים נמדד, ויכולת מדידת עיבורים באופן מקומי.
- היכרות עם מכשור המדידה וכיצד המאפיינים (specifications) שלו משפיעים על דיוק הניסוי. בפרט, השפעת צפיפות הכתמים (speckles), גודל ה subset, ורדיוס המיצוע של העיבורים על הדיוק של מדידות באמצעות DIC.
- הבנת המשמעות של ריכוז מאמצים והתפלגות עיבורים והכרת האתגרים במדידה שלהם. הכרת התפלגות מאמצים בסביבת סדק והמושג של מקדם עוצמת המאמצים.
מערכת הניסוי ותיאור תהליך הניסוי
תיאור עקרוני של שיטות המדידה
מדי עיבור (Strain Gauges)
שיטה זו מבוססת על שינוי ההתנגדות החשמלית של חוט כתוצאה משינוי באורכו. עבור חומרים מתכתיים, קיים יחס לינארי בין שינוי ההתנגדות לבין העיבור, המתואר במשוואה:
כאשר:
אם אנו משתמשים במדיד יחיד ללא מעגל חשמלי נוסף, אז עקב הפעלת עיבור
כאשר
כאשר
פוטואלסטיות (Photoelasticity)
חלק מהחומרים מראים שינוי לינארי במקדם השבירה של אור תחת עיבור, תופעה הנקראת פוטואלסטיות. כאשר מעבירים קרן אור מְקֻטָּב דרך חומר פוטואלסטי מעובד, מתקבל הבדל במקדמי השבירה בכיוונים שונים וכתוצאה מכך נצפים פרינג’ים (fringes) - פסים צבעוניים בעלי סדר מוגדר - המעידים על הפרשי מאמצים במודל.
סדר ה-
בהינתן סדרי הפרינג’ים, נוכל לחשב את מקדם ריכוז המאמצים באמצעות
כאשר:
קורלציה של תמונות דיגיטליות (Digital Image Correlation, DIC)
טכניקה אופטית למדידת שדה תזוזות על פני דגם. הדגם מצופה בכתמי צבע (speckles) בעלי גודל אחיד, צורה אקראית וניגודיות גבוהה. באמצעות מעקב אחר תנועת כתמים אלו תחת עומס מתקבלת מפת עיבורים. ישנו trade-off בין רזולוציית המדידה לבין רזולוציה מרחבית: רזולוציה טובה יותר דורשת subsets קטנים יותר.
תיאור מערכת הניסוי
מערכת הניסוי כוללת:
- מתקן מתיחה להעמסת דגמים בעומסים שונים.
- מצלמה דיגיטלית לצורך מדידות DIC.
- פולריסקופ (Polariscop) למדידות פוטואלסטיות.
- חיישן כוח מסוג Load Cell B3G למדידת הכוח המופעל.
- מדי עיבור (strain gauges) להדבקה ולמדידה ישירה של העיבורים.
במהלך הניסוי הראשון, נשתמש בדגם מלבני עם חור מרכזי:
- חצי דגם מצופה speckles עבור מדידות DIC.
- החצי השני נמדד בשיטת הפוטואלסטיות.
- בנוסף, נמדדים עיבורים נקודתיים באמצעות מדי עיבור.
במהלך הניסוי השני, יבוצעו מדידות נוספות על דגמי עצם-כלב ודגם עם חריץ (notch) להשוואה בין שלוש שיטות המדידה.
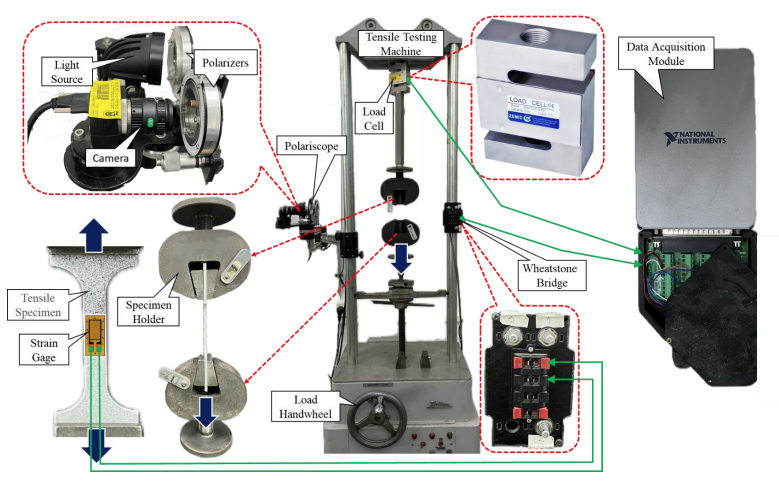
איור 1: מערכת הניסוי.
ניתוח מפרטי החיישנים והערכת השגיאה הצפויה
החיישן Load Cell B3G משמש למדידת הכוחות המופעלים על הדגמים. מהנתונים הטכניים של החיישן ניתן להעריך כי שגיאות המדידה נובעות מהפרעות כגון:
- אי-ליניאריות.
- הִיסְטֵרֵזָה (hysteresis).
- רגישות לטמפרטורה.
- שגיאת אפס.
לפי המפרט, סך השגיאות הצפויות הן עד
דיון במקורות לשגיאות בניסוי
מקורות השגיאות האפשריים כוללים:
- מדי עיבור: שגיאות שיטתיות עקב הדבקה לא תקינה או אי-אחידות בעיבור על פני החיישן; שגיאות אקראיות בגלל רעש חשמלי.
- שיטת DIC: שגיאות אקראיות בתהליך חישוב העיבורים (עקב רעש מדידה או איכות speckles נמוכה), שגיאות שיטתיות אם התנועה מחוץ למישור משמעותית.
- פוטואלסטיות: שגיאות שיטתיות עקב אי-דיוק בקריאת סדרי ה-fringes.
- חיישן Load Cell: שגיאות שיטתיות עקב סטיות במקדם הכיול, ושגיאות אקראיות עקב רעידות או השפעות טמפרטורה.
בהתבסס על השפעת כלל מקורות השגיאה, ניתן להעריך כי דיוק המדידות הכולל יעמוד על לפחות
ניתוח תוצאות
ניסוי עם דגם המכיל קדח עגול
הניסוי שלנו התחלק ל-3 חלקים. שימוש במדי עיבור, פוטואלסטיות ו-DIC.
ראשית נסתכל על הניסוי של המד-עיבור.
מדי עיבור
-
האות המתקבל מהמדי-עיבור (לאחר גשר ויטסטון) הוא מתח, לכן תחילה נמיר את המתח שקיבלנו לעיבורים באמצעות משוואה (L1.6):
כאשר אצלנו:
עבור כל מדיד (שניים בסך הכל, אחד עבור עיבור מקסימלי ליד החור ב-
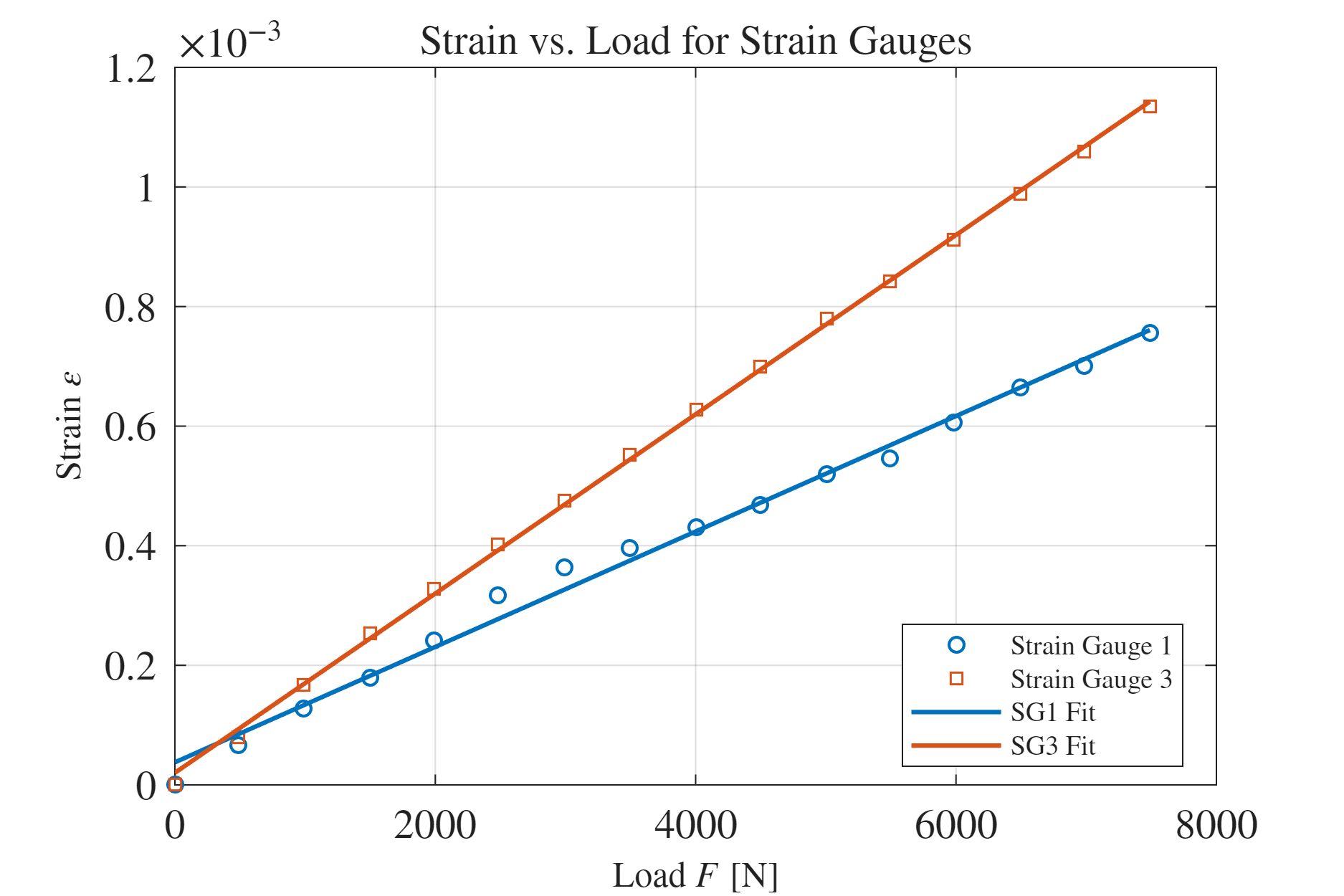
איור 2: עיבור כתלות בעומס.
-
מהרגרסיה קיבלנו:
כאשר
לפי התוצאות שקיבלנו נוכל לטעון שמידת ההתאמה לחוק הוק הינה טובה, ולכן אנו בתחום האלסטי. -
משיפוע זה, שגיאתו, ושגיאת מדי העיבור העומדים על
-
בהנחה והרזולוציית מדידת מתחים של המדי-עיבור עומדת על
לעומת זאת, לפי ההרצאה, ל-DIC יש רזולוציה העומדת על:
לפיכך, התוצאות שיניבו מדי-העיבור מתאימות יותר לניסוי זה.
בנוסף, משתמע מכך שהשגיאה האקראית בשיטת DIC גדולה יותר.
שיטת DIC
בניתוח התוצאות עבור DIC, בחרנו להשתמש ברדיוס המיצוע (subset radius) בגודל

>איור 3: מפת עיבורים של
- בעזרת תכנת ncorr דגמנו שלוש נקודות בקרבת המאמץ המקסימלי (ב-
-
באמצעות מפת העיבורים שהתקבלה מה-DIC, נחשב את פרופיל העיבור לאורך הקו
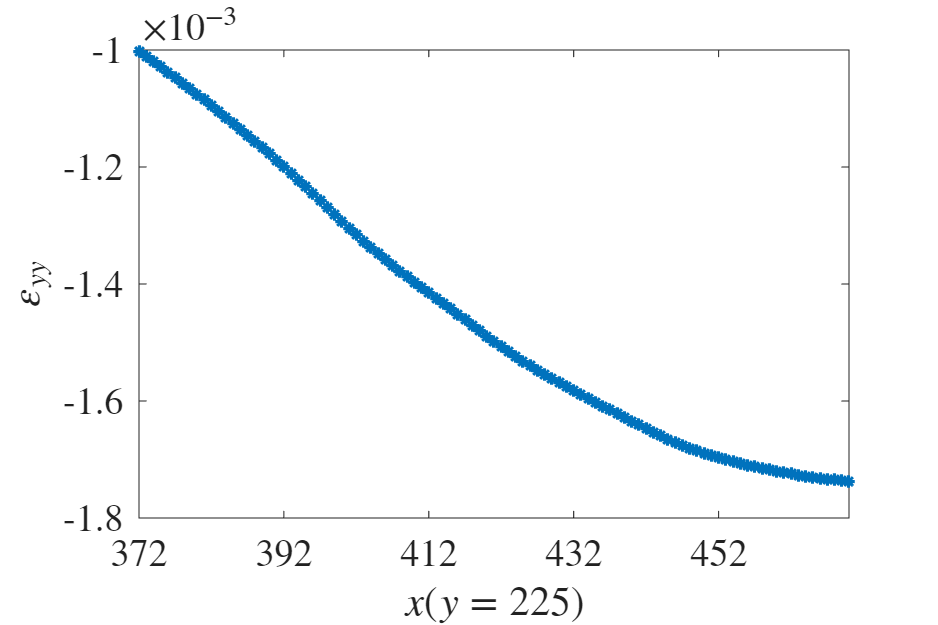
איור 4: פרופיל העיבור לפי DIC ב-
לפי משוואה (L1.2), הפרופיל האנליטי עבור
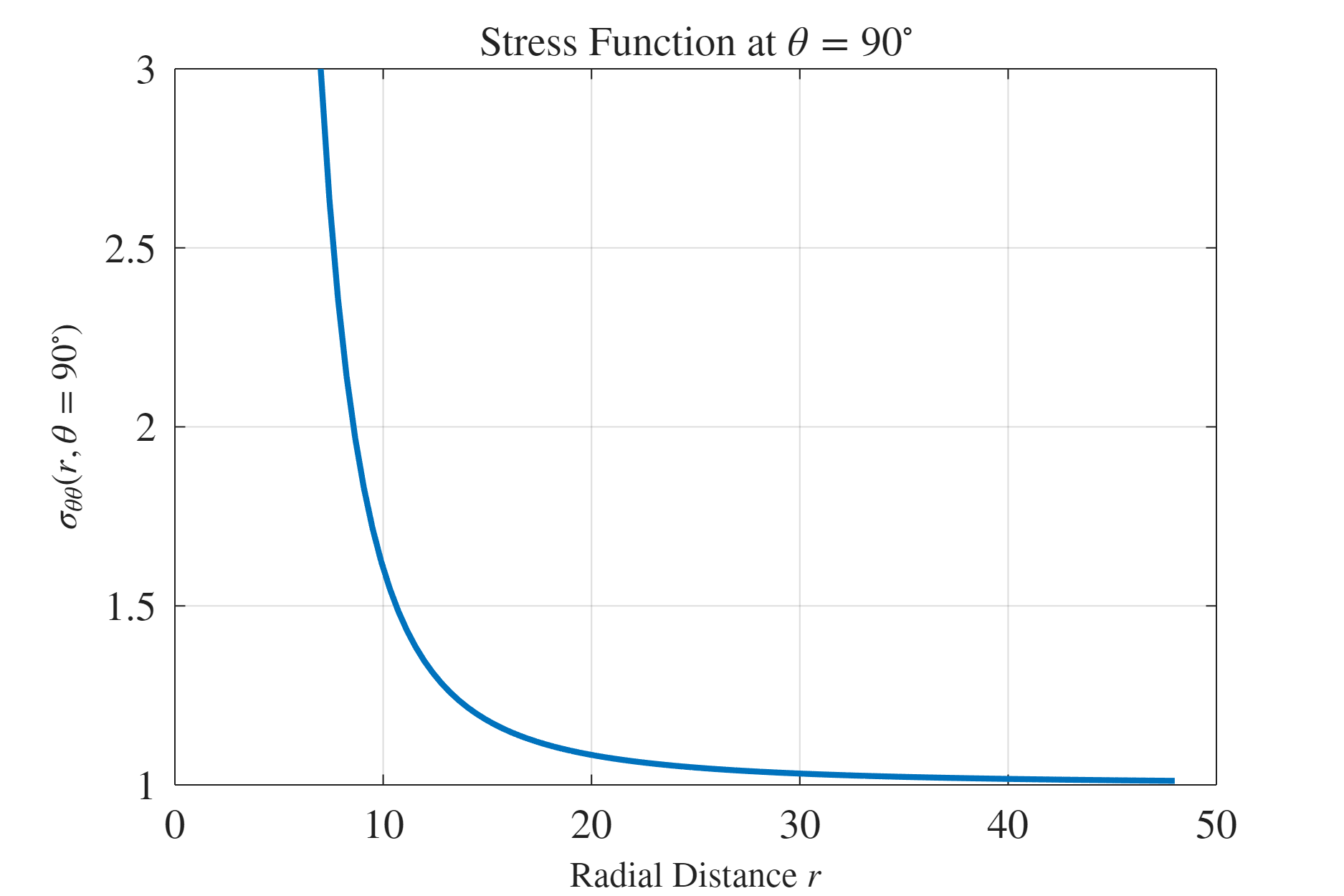
איור 5: פרופיל המאמץ לפי Kirsch ב-
קיבלנו שוני משמעותי בין הפרופיל של שני הגרפים, שלהערכתנו הוא כתוצאה מהעובדה שאנו לא עובדים עם לוח אינסופי כמו בהנחות Kirsch וכתוצאה משגיאות מדידה וניתוח בשיטת ה-DIC. כמו כן, הדגם עליו ביצענו את הניתוח עבר את אותו הניסוי מספר רב של פעמים, ולכל הנראה נשארו בו עיבורים שיוריים שמשפיעים ישירות על תוצאות הניסוי.
פוטואלסטיות
הערה:
את שיטת הפוטואלסטיות להלן ביצענו על דגם שונה מהדגם עליו ביצענו את ניסויי מדי-העיבור וה-DIC בשל תקלה בעמדה עליה ביצענו את ניסויים אלו.
-
ننתח את סדרי הפרינג’ים בכל אזור בתמונת הפוטואלסטיות.
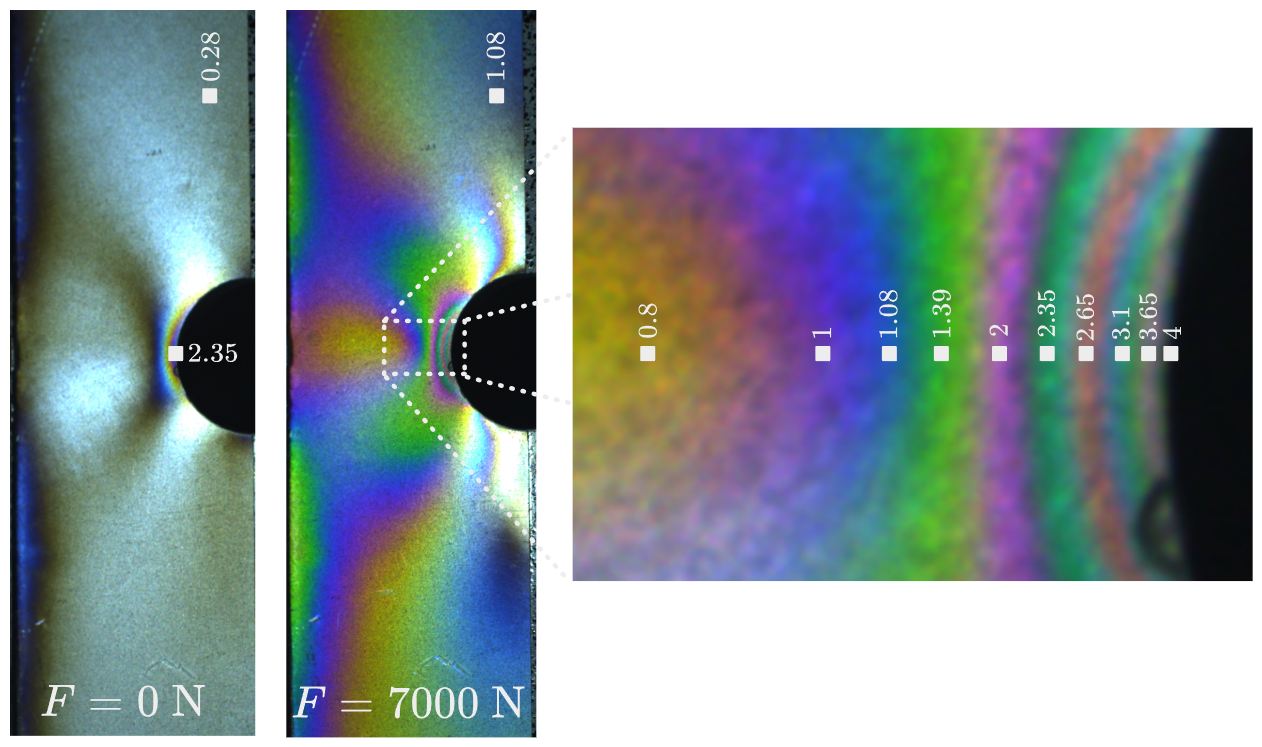
איור 6: ניתוח פוטואלסטי.
ראשית, חילקנו את הדגם לאזורי צבעים בולטים בעזרת הטבלה לסדרי fringes:
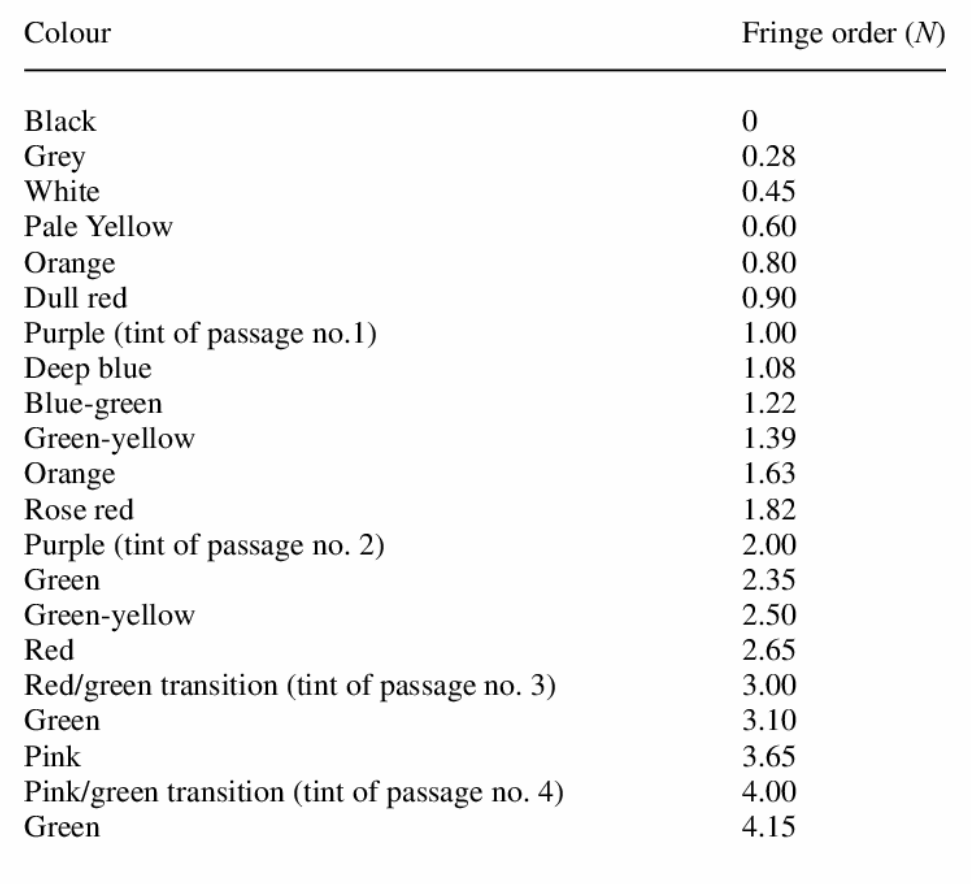
איור 7: סדרי fringes.
אנו יודעים לפי התאוריה (Kirsch) שב-
-
מסדרי ה-fringes נוכל לחשב את ריכוז המאמצים באמצעות משוואה (L1.7). לפי חישוב מקדם ריכוז המאמצים מפוטואלסטיות בנספחים נקבל:
קיבלנו שגיאה יחסית גבוה העומדת על כ-
נמיר כל ערך
קיבלנו אי-התאמה בין השיטות שיכולה לנבוע מהעובדה שמד העיבור המקסימלי ממוקם בצד השני של החור, אבל היא לכל הנראה בעיקר מכך שאת שיטת הפוטואלסטיות ביצענו על דגם שונה ממדי-העיבור.
השוואה לתאוריה
-
על פי פתרון Kirsch, משוואה (L1.2), מקדם ריכוז המאמצים (לאחר הצבה
לפי (Bi et al., 2020), במקרה שבו רוחב הפלטה
במקרה שלנו
נחשב את הערך הנומינלי והשגיאה לפי חישוב שגיאה תאורטית בנספחים:
נחשב את ה- Student T Test לכל אחד מהתוצאות לפי:
קיבלנו:
הפערים המשמעותיים בין הערכים הניסיוניים (
- גיאומטריה סופית מול אינסופית: פתרון Kirsch מניח לוח אינסופי (
- אלסטיות לינארית: המודלים מניחים התנהגות אלסטית לחלוטין. בפועל, באזור ריכוז המאמצים סביב הקדח, ייתכנו מאמצים גבוהים הגורמים לעיוותים פלסטיים מקומיים, במיוחד בעומסים גבוהים יותר. התנהגות זו אינה נלקחת בחשבון במודל האלסטי.
- מדי עיבור (SG): המדיד מודד עיבור ממוצע על פני שטחו, ולא את ערך השיא הנקודתי בקצה הקדח. דיוק המיקום של המדיד קריטי. כמו כן, קיימת אי-ודאות במקדם הרגישות (
- קורלציית תמונות דיגיטלית (DIC): התוצאה מושפעת מגודל ה-subset, איכות ה-speckles, תזוזות מחוץ למישור, ותנאי תאורה. האלגוריתם עצמו מכניס שגיאות חישוב.
- פוטואלסטיות (PE): שיטה זו פחות מדויקת מטבעה ומיועדת להערכה איכותית. חשוב לציין שמדידה זו בוצעה על דגם שונה, דבר הפוגע ביכולת ההשוואה הכמותית הישירה.
- מצב הדגם: כפי שצוין, הדגם עליו בוצעו מדידות ה-SG וה-DIC עבר שימוש חוזר, וייתכן שקיימים בו עיבורים שיוריים או נזק מקומי המשפיעים על התוצאות.
- שגיאות ניסוי כלליות: אי-דיוקים במדידת הכוח המופעל (Load Cell), יישור לא מושלם של הדגם במתקן המתיחה, ועוד.
- גיאומטריה סופית מול אינסופית: פתרון Kirsch מניח לוח אינסופי (
יתרונות וחסרונות של כל שיטה
-
יתרונות וחסרונות של שיטות המדידה:
- מדי עיבור (SG): יתרונות - דיוק נקודתי גבוה, רזולוציית עיבור טובה (כ-
- קורלציית תמונות דיגיטלית (DIC): יתרונות - מיפוי שדה עיבורים מלא, מאפשר ויזואליזציה של אזורי ריכוז ופלסטיות. חסרונות - רזולוציית עיבור נמוכה יחסית (כ-
- פוטואלסטיות (PE): יתרונות - הדמיה איכותית ומיידית של אזורי ריכוז מאמצים. חסרונות - בעיקר איכותני, קשה לכימות מדויק, דורש דגם שקוף או ציפוי מתאים.
שיפורים אפשריים: שימוש באותו דגם לכל המדידות (SG, DIC, PE) חיוני להשוואה ישירה. דיוק במיקום מדי העיבור. אופטימיזציה של פרמטרי DIC (גודל subset, איכות speckles). ביצוע אנליזת אלמנטים סופיים שתביא בחשבון גיאומטריה סופית ואולי גם פלסטיות, לצורך השוואה תאורטית מדויקת יותר.
- מדי עיבור (SG): יתרונות - דיוק נקודתי גבוה, רזולוציית עיבור טובה (כ-
ניסוי עם דגם עצם-כלב במתיחה לכשל
-
באותו האופן כמו הניסוי הקודם:
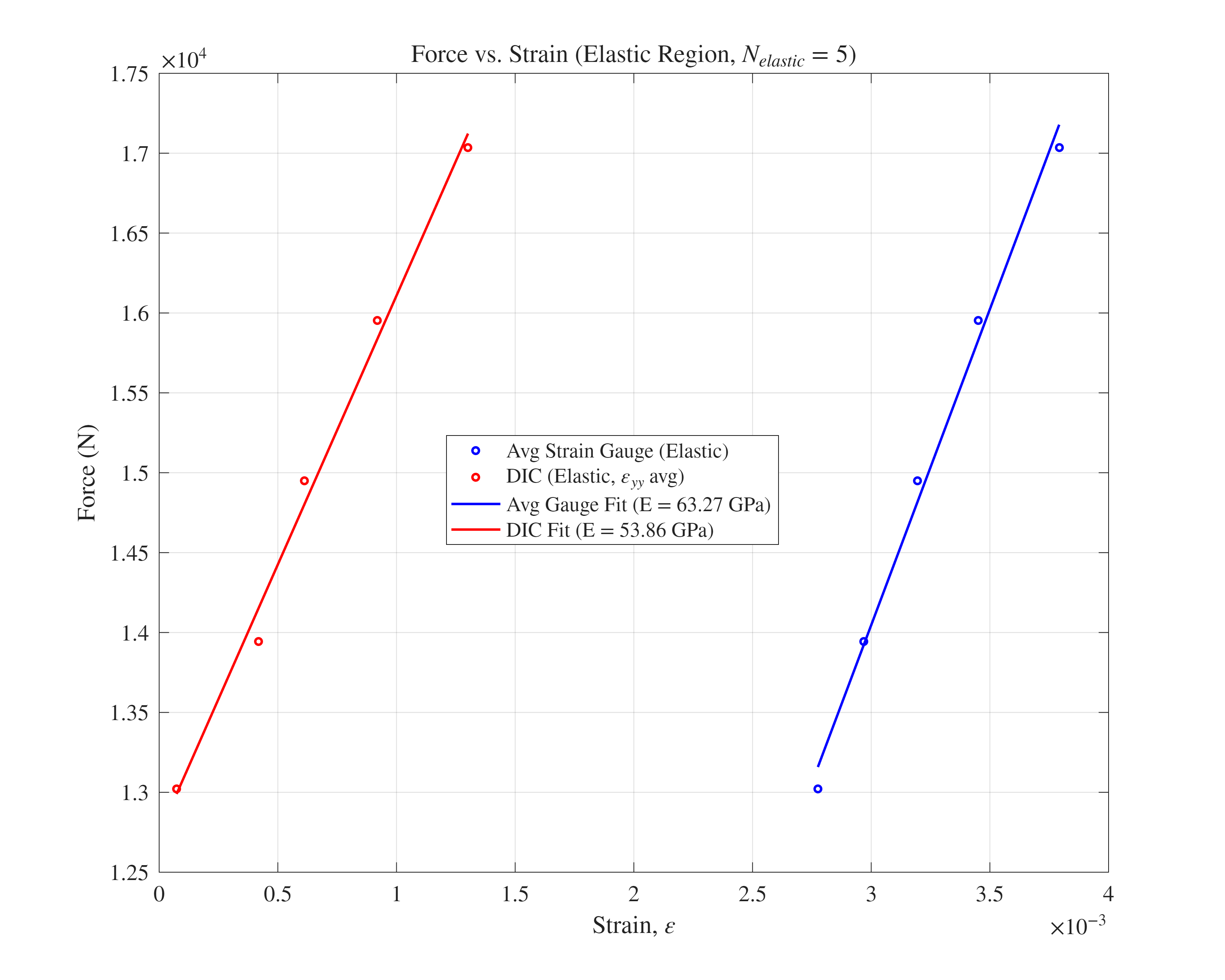
איור 8: כוח מול עיבור באזור האלסטי.
-
אם נביט בכלל התוצאות:
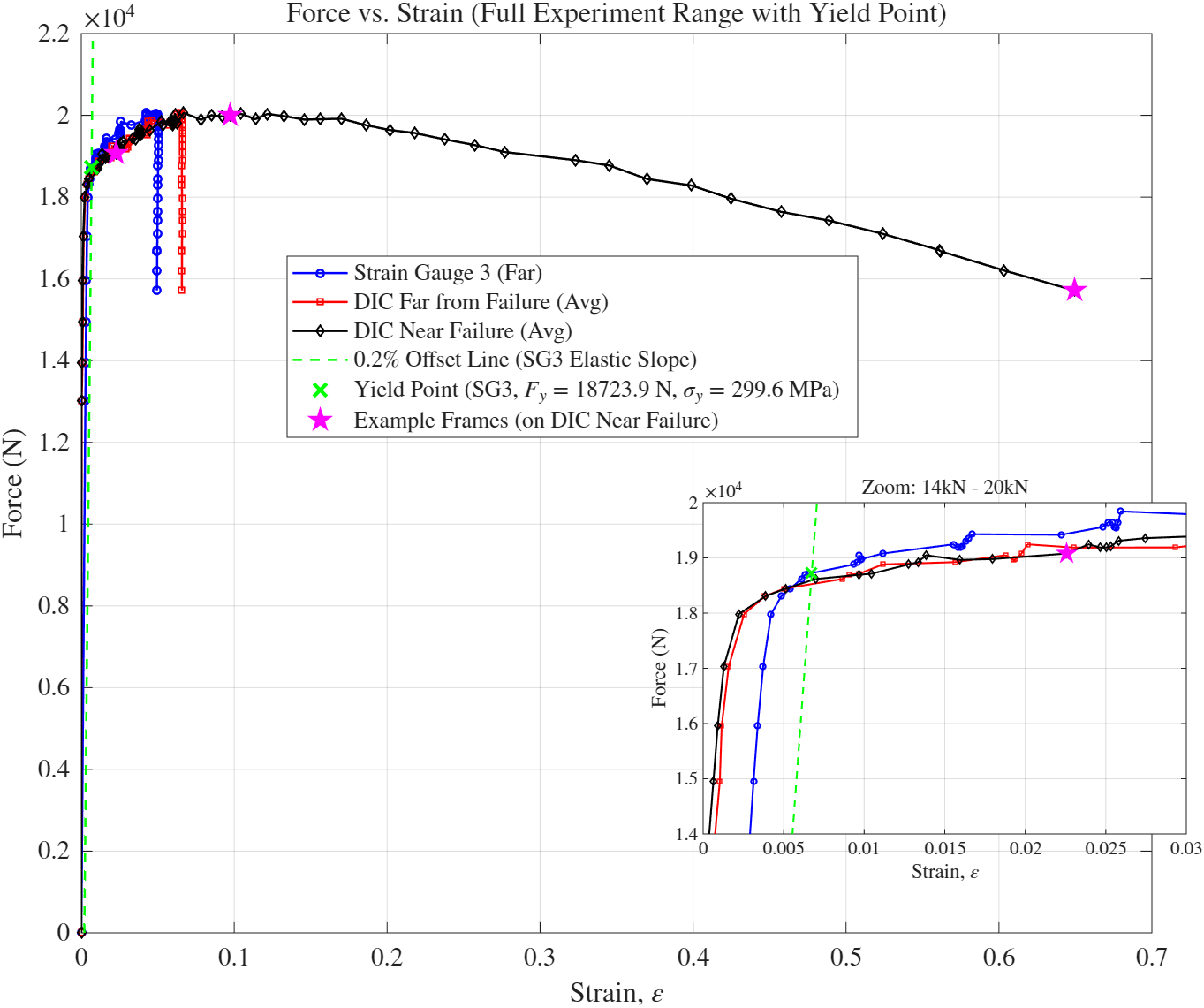
איור 9: כוח מול עיבור בכלל תחום המדידה, עם הגדלה של אזור הכניעה.
-
תמונות מה-DIC:
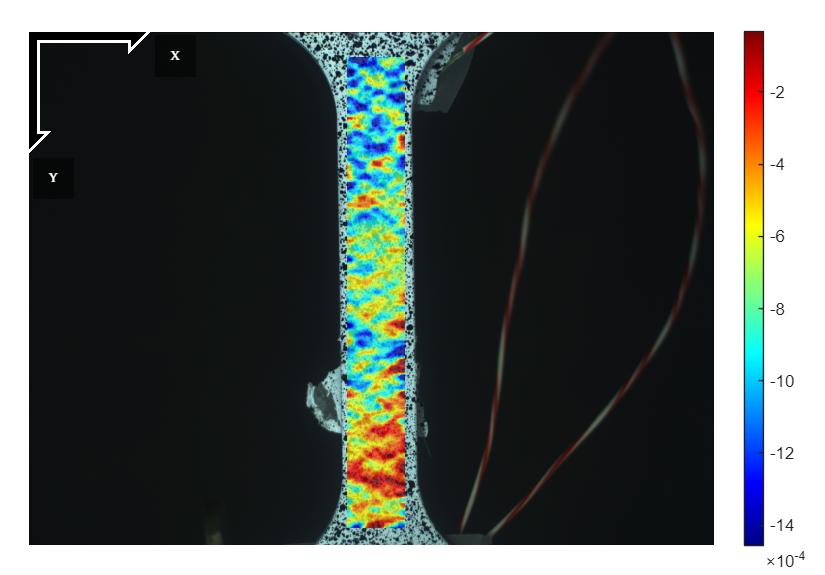
איור 10: הדגם תחת עומס
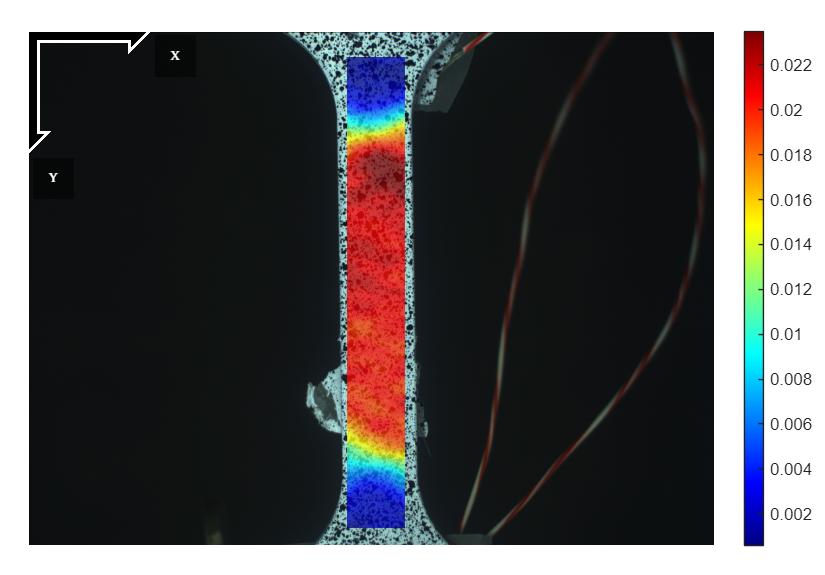
איור 11: הדגם תחת עומס
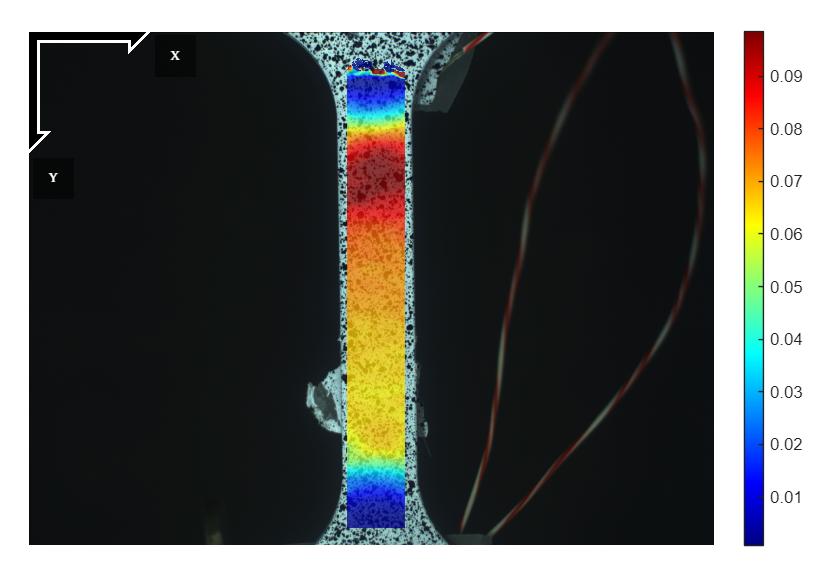
איור 12: הדגם תחת עומס
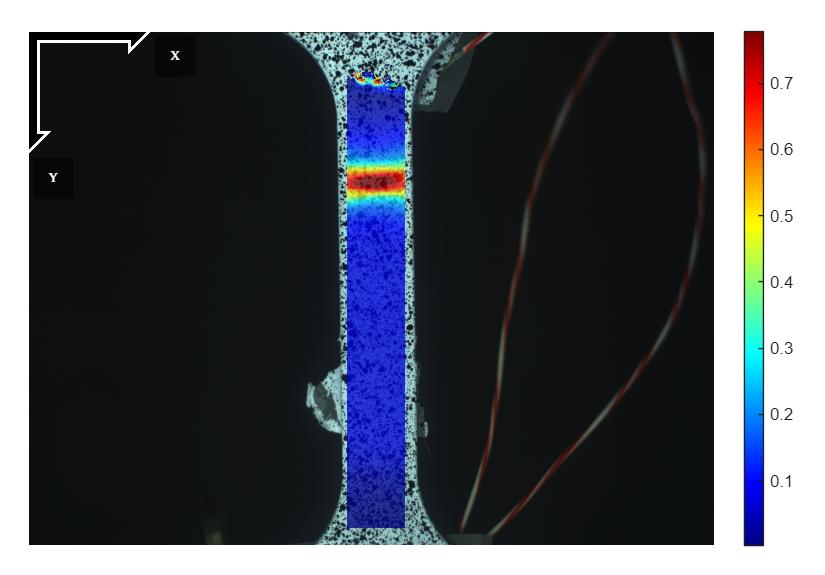
איור 13: הדגם תחת עומס
4. נעבור כעת לחישוב המודול יאנג. לפי חישוב מודול יאנג מרגרסיה לינארית מהנספחים, נקבל שעבור כל שיטה הוא:כדי לחשב את מאמץ הכניעה, נרצה קודם למצוא את עומס הכניעה. באיור 9, הוא מסומן ב-
-
לפי נספח א’ בהנחיות למעבדה, הדגמים יוצרו מפלטת פלדת אלומיניום T6-6061. מהספרות, מודול יאנג שלו הוא
ע”מ להשוות בין הערכים שקיבלנו לערכי הספרות, נשתמש במבחן t. נקבל: -
בהתבסס על ניתוח שיטות המדידה לאיור 9, המתאר את הכוח כפונקציה של העיבור לאורך כל שלבי הניסוי (כולל הכשל), שיטת DIC מספקת תיאור מדויק ומעמיק יותר של התפלגות העיבורים ושל התהליך המתרחש באזור הכשל. שיטה זו מאפשרת מדידת שדה העיבורים על פני שטח הדגם כולו, ובפרט מאפשרת בחינה מקומית באזור היווצרות הכשל. תהליך הכשל במתיחה מתאפיין בהתפלגות לא אחידה של עיוותים פלסטיים, אשר מתרכזים באזור צר ויוצרים necking. שיטת DIC מאפשרת מעקב אחר התפתחותו ואחר העלייה המקומית בעיבור באזור הצר.
לעומת זאת, מדדי-העיבור מספקים מדידה מקומית בלבד ומתאימים בעיקר לעיבורים קטנים בתחום האלסטי (הקטנים מ-
לכן, בניסוי זה נעדיף את שיטת DIC, שכן היא מאפשרת חילוץ של מפה מרחבית וכמותית של העיבורים, ובפרט באזור הכשל.
ניסוי עם דגם עם חריץ
-
בניסוי זה, תחת העומס הגבוה ביותר, קיבלנו תוצאה שאיכותית, מאוד דומה למודל התאורטי:
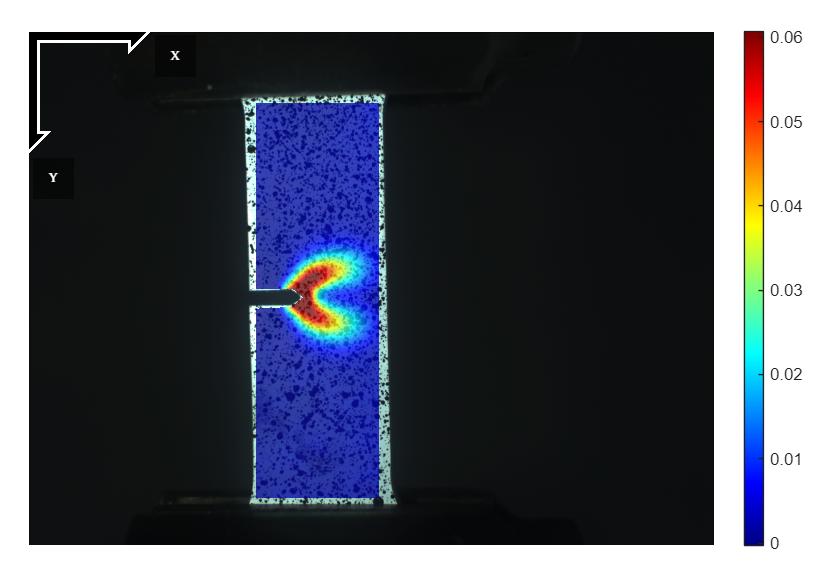
איור 14: מפת עיבורים של הדגם תחת עומס
-
ניתן לראות כי קיימת התאמה איכותית בין מפת העיבורים שהתקבלה במדידה באמצעות DIC לבין ההתפלגות התאורטית של המאמצים המוגדרת במשוואות (L1.3) ו-(L1.4). התאמה זו באה לידי ביטוי בכך שגם המדידה וגם המודל מצביעים על ריכוז מאמצים ועיבורים באזור קצה החריץ, שהוא האזור הקריטי שבו מתפתח הכשל.
עם זאת, קיימים הבדלים בין ההתפלגות המתקבלת בפועל להתפלגות התאורטית. ראשית, המודל התאורטי מניח סדק חד (רדיוס עקמומיות) בפלטה אינסופית, בעוד שבפועל מדובר בחריץ בעל רדיוס סופי בקצהו ובדגם בעל ממדים מוגבלים. שנית, התאוריה מניחה התנהגות אלסטית של החומר בכל התחום, אך בפועל, בקרבת קצה החריץ נצפים עיוותים פלסטיים כתוצאה ממאמצים גבוהים, והתנהגות זו אינה נכללת באזור האלסטי. לבסוף, שיטת DIC עצמה כוללת מגבלות טכניות - מיצוע על פני תת-אזורים, רזולוציה סופית, והשפעות של רעש מדידה - אשר תורמות להחלקה של השדה המתקבל ולסטייה מהתיאוריה.
-
נמצא את פרופיל העיבור לאורך הקו האופקי
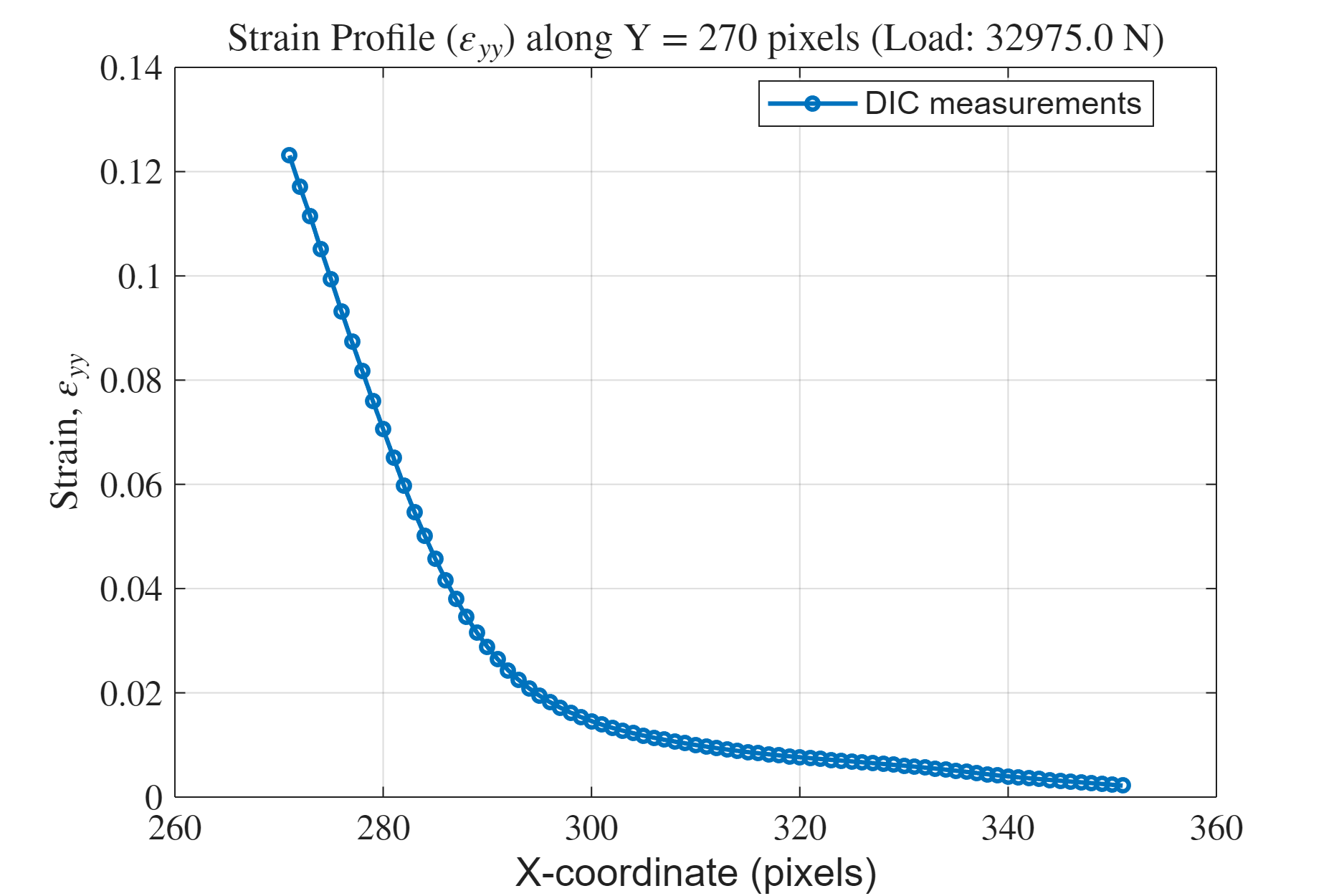
איור 15: פרופיל העיבור לאורך
לפי המודל התאורטי (משוואות (L1.3) ו-(L1.4)), עבור סדק חד בפלטה אינסופית תחת עומס מסוג
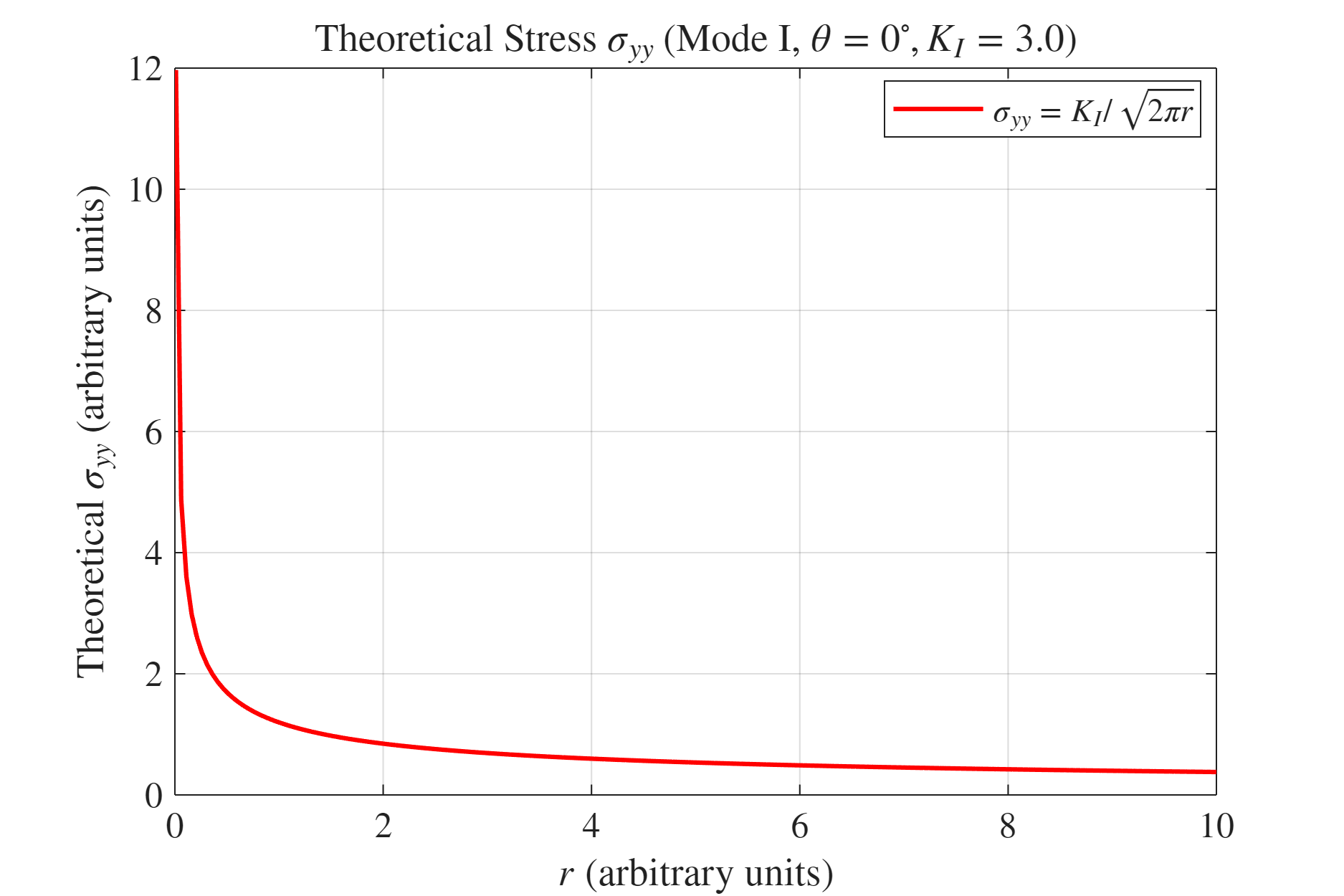
איור 16: פרופיל המאמץ לאורך
נשים לב שההתאמה לתאוריה היא איכותית בלבד. לגרף מ-DIC אין שיפוע כל כך חד בסמוך לחריץ, ורק רחוק ממנו, במאמצים שלכל הנראה עדיין בתחום האלסטי, ישנה דעיכה דומה לתאוריה.
-
נבחן כמותית את התאוריה ע”י הקשר הלוגריתמי הבא שפותח בנספחים:
כלומר, כאשר נשרטט את
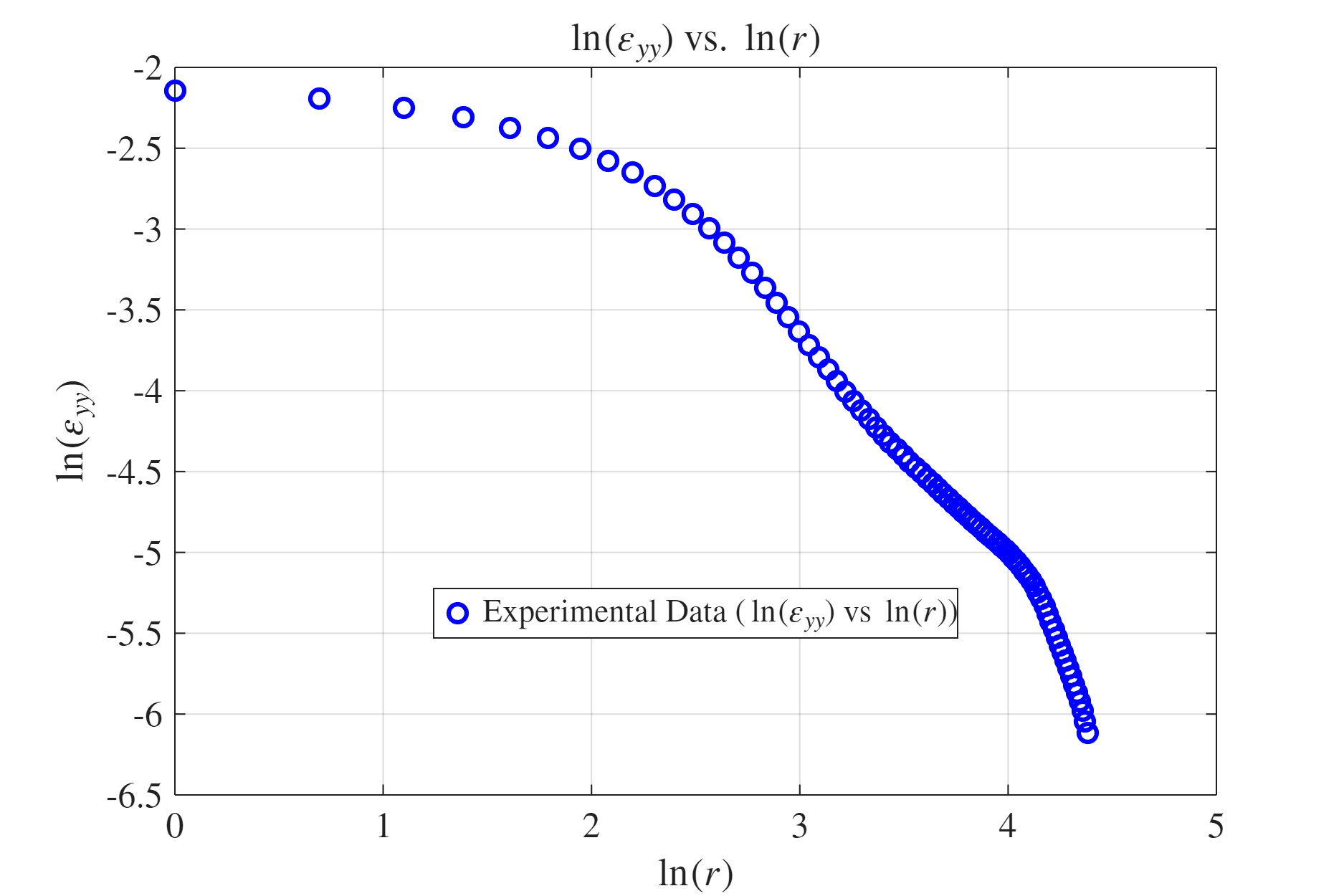
איור 17: קשר לוגריתמי בין עיבור למרחק מהחריץ.
ניתן לראות מהגרף כי יש קשר לינארי רק בחלקו. נתמקד באזור זה ונמצא את השיפוע.
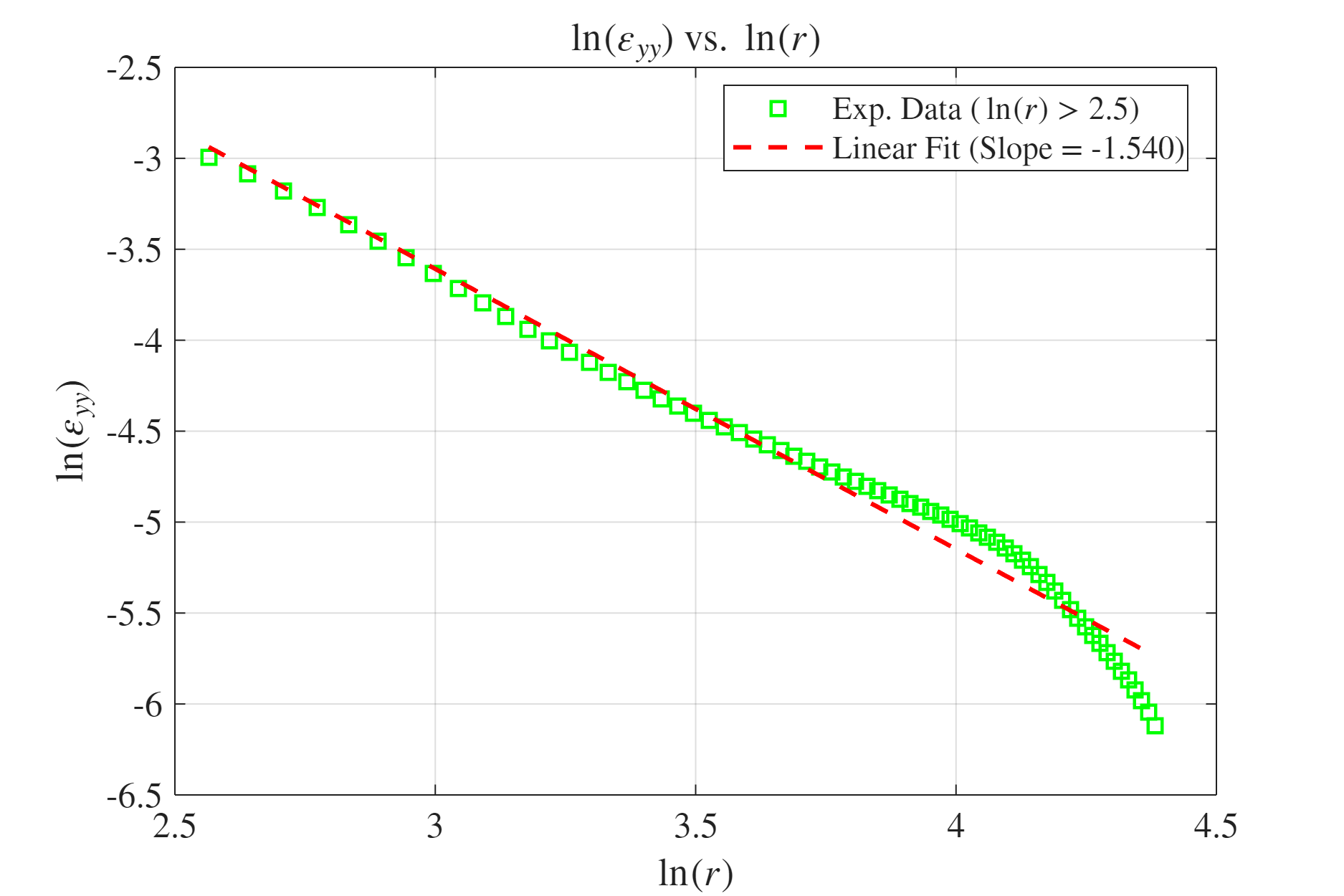
איור 18: קשר לוגריתמי בין עיבור למרחק מהחריץ ב-
בהשוואה לתאוריה, קיבלנו שיפוע רחוק מהמצופה, שנובע בעיקר מהנחה שגויה של אלסטיות ושל פלטה אינסופית.
סיכום ומסקנות
במסגרת מעבדה זו נבחנו שלוש שיטות למדידת עיבורים – מדי עיבור (SG), קורלציית תמונות דיגיטלית (DIC) ופוטואלסטיות (PE) – תוך התמקדות בתופעות של ריכוז מאמצים והתנהגות חומרים תחת עומס.
איחוד מסקנות והשוואה בין פרקי הדוח:
-
הערכת שגיאות: הערכת השגיאה הראשונית, שהתבססה בעיקר על מפרט חיישן הכוח (כ-
-
התאמה לתיאוריה:
- ריכוז מאמצים (קדח): מקדמי ריכוז המאמצים שנמדדו (
- אלסטיות ופלסטיות: חוק הוק תאר היטב את התנהגות מדי העיבור בתחום המדידה בניסוי הקדח (
²
- ריכוז מאמצים (קדח): מקדמי ריכוז המאמצים שנמדדו (
נספחים
חישוב מקדם ריכוז המאמצים ממדי עיבור
נחשב את מקדם ריכוז המאמצים לפי הגדרתו, משוואה (L1.1):
לפי חוק הוק:
נציב את העיבורים שקיבלנו ונמצא כי לפי מדי-העיבור:
כדי לחשב את השגיאה האקראית, נשים לב של-
ולכן השגיאה הנגררת של
חישוב מקדם ריכוז המאמצים מפוטואלסטיות
לפי הניתוח שביצענו באיור 6, ומשוואה (L1.7):
בהנחה והשגיאה שלנו בבחירת סדרי ה-fringes עומדת על
חישוב קשר בין מדידות מדי העיבור והפוטואלסטיות
עבור מד-העיבור והניתוח הפוטואלסטי, העיבורים בעומס המקסימלי הם:
ולכן:
חישוב שגיאה תאורטית
על מנת לחשב את השגיאה התאורטית של הפתרון הנומרי
ניקח בחשבון את שגיאות המדידה של קוטר החור ורוחב הדגם.
השגיאה הנגררת היא:
כדי לפשט את החישוב, נגדיר משתנה עזר
הנגזרת של
הנגזרות החלקיות של
באמצעות כלל השרשרת, נחשב את הנגזרות החלקיות של
לאחר הצבת הערכים מתקבל:
לכן:
נקבל ששגיאת
חישוב מודול יאנג מרגרסיה לינארית
היות והוא מוכל בשיפוע של גרף עומס-עיבור, באופן הבא
לפי קשרי מאמץ-עיבור, בתחום האלסטי מתקיים
מדדנו את שטח החתך:
השגיאה הנגררת:
נקבל כי השטח חתך:
מהרגרסיה הליניארית אנו יודעים לחלץ את השיפוע
פיתוח הקשר הלוגריתמי בין עיבור לרדיוס
לפי משוואה (L1.3):
בתחום האלסטי, לפי קשרי מאמץ עיבור:
נפעיל
או פשוט:
ביבליוגרפיה
- Kirsch, G. (1898). Die theorie der elastizität und die bedürfnisse der festigkeitslehre. Springer. https://books.google.co.il/books?id=pvBuPwAACAAJ
- Bi, Z., Pilkey, W. D., & Pilkey, D. F. (2020). Peterson’s stress concentration factors (Fourth edition). John Wiley & Sons, Inc.
