1
מספר קורס 01140032 מספר קבוצה 54 עמדת עבודה 23 שם מדריך רז עמר מגישים עידו פנג בנטובCLASSIFIED CLASSIFIED תאריך 23/04/2025 דוח מסכם לניסוי מטוטלת פשוטה
תקציר
מטרת הניסוי הייתה לבחון את הקשר בין אורך חוט המטוטלת לבין זמן המחזור שלה, בהתאם למודל של מטוטלת מתמטית.
You can't use 'macro parameter character #' in math mode T=\sqrt{ \dfrac{g}{\ell} } \tag{1} $$ [^2] הממצאים שהתקבלו תאמו את הציפיות התאורטיות, ואישרו את ההנחות שהמטוטלת אכן מתנהגת כמטוטלת מתמטית במסגרת התנאים שנבדקו. [^3] [^2]: נוסחאות מופיעות רק במבוא או בנספחים [^3]: זו מסקנה מתוצאות הניסוי וזה לא צריך להיות כאן. צריך לכתוב "והשוונו את התוצאות שלנו לתאוריה". # מבוא מטוטלת פשוטה היא מערכת הכוללת מסה $m$ התלויה בקצה חוט דק הנתונה להשפעת כוח הכבידה $g$, כאשר אורך החוט $\ell$ נמדד מנקודת הציר ועד למרכז המסה של המשקולת. ![[LPH1_L001 מטוטלת פשוטה 2025-04-25 09.49.39.excalidraw.svg]]^figure-fbd >איור 1: מערכת מטוטלת מתמטית. מערכת הניסוי שלנו כללה כדור פלדה בקוטר התלוי על חוט דייג שקשור בשני צדדיו למוט מתכתי אופקי על מנת לאפשר תנועה במישור אחד בלבד. המוט האופקי מחובר למוט אנכי המוצמד ע"י מגנט לשולחן העבודה. ![[{C0DF44D5-AC05-4562-B24C-F47348B6EA11}.png|350]]^figure-lab-picture >איור 2: מערכת המדידה לניסוי. למדידת הגדלים הפיזיקליים השתמשנו בקליבר, סרגל, מד-משקל ושעון-עצר עם תזמון אנושי. הניסוי הסתמך על מספר הנחות תאורטיות: 1. מסת החוט זניחה ביחס למסת המשקולת. 2. קוטר המשקולת זניח ביחס לאורך החוט. 3. החיכוך (עם האוויר ועם חלקי המערכת) ניתן להזנחה. 4. המשקולת נעה בזוויות קטנות, כך שניתן לקרב את סינוס הזווית לערך הזווית עצמה. 5. התנועה מתבצעת במישור אחד בלבד. כדי לבדוק את תקפות המודל, מדדנו את זמן המחזור של המטוטלת עבור מספר אורכי חוט שונים. כדי להקטין את שגיאות המדידה הנובעות מתגובה אנושית ושעון העצר, מדדנו את הזמן של עשרה מחזורים בכל הרצה וחילקנו את הזמן הכולל בעשר. באמצעות אנליזת ממדים התקבל קשר מהצורה: T=\text{const} \cdot\ell^{\alpha } \tag{2}
כ א ש ר ה ו א ז מ ן ה מ ח ז ו ר ב ו ה ו א א ו ר ך ה ח ו ט ב מ ש ו ו י ו ן מ מ ד י ם א נ ו מ צ פ י ם ל ק ב ל ל א ח ר מ כ ן ב ו צ ע ה ל י נ א ר י ז צ י ה ל מ ה ב ו צ ע ה ה ל י נ א ר ז י צ י ה ו מ י א ל ו ה ג ד ל י ם ה א ו פ י י נ י י ם ה א ל ו ו נ ר מ ו ל ל פ י ג ד ל י ם א ו פ י י נ י י ם ל ק ב ל ת מ ש ו ו א ה מ ה צ ו ר ה \ln\left( \dfrac{T}{T^{}} \right)=\alpha \ln\left( \dfrac{\ell}{\ell^{ }} \right) \tag{3}
You can't use 'macro parameter character #' in math mode כאשר $\ell^{*}$ ו-$T^{*}$ הם הגדלים האופייניים של הביטויים המתאימים. <div><hr><hr></div> # תוצאות הניסוי ## הכנות לניסוי ^[בכל הדוח צריך להיות רק כותרות של: הכותרת עצמה, תקציר, מבוא, תוצאות, דיון] כהכנה לניסוי מדדנו את את מסת המשקולת, מסת החוט, קוטר המשקולת ואורך החוט. \begin{aligned}{\text{string}}<0.01\cdot \pu{e-3kg} \[1ex] {1}=(20\pm 0.1)\cdot \pu{e-3m} \[1ex]
You can't use 'macro parameter character #' in math mode כאשר $m$ היא מסת המשקולת, ${m}_{\text{string}}$ היא מסת החוט, $d$ הוא קוטר כדור הפלדה, ו-${\ell}_{1}$ הוא אורך החוט ההתחלתי, שהוא גם אורך החוט הכי קצר שנשתמש בניסוי. בנוסף, אנו מניחים $\delta{T}_{\text{tot}}=\pu{0.3s}$, כאשר ${T}_{\text{tot}}$ הוא סך הזמן הנמדד, כהחמרה על זמן התגובה האנושי הממוצע שעומד על $\sim \pu{0.2s}$. ניתן לראות שמתקיים $m\gg {m}_{\text{string}}$ וגם ${\ell}_{1}\gg d$ ולכן מתקיימות ההנחות שמסת החוט זניחה ביחס למסת המשקולת וקוטר המשקולת זניח ביחס לאורך החוט. רצינו לבחור זווית שתקיים את ההנחת זוויות קטנות. בחרנו באורך ${\ell}_{1}$ (כאשר הסימון $1$ הוא עבור האורך הראשון שבחרנו, בניסוי בהמשך הוא משתנה), ושחררנו את המטוטלת מ-$9$ זוויות התחלה שונות, מ-$90^{\circ}$ עד $10^{\circ}$ בהפרשים של $10^{\circ}$. מדדנו את זמן המחזור הממוצע מתוך $10$ מחזורים לכל זווית והזנו את התוצאות לתוכנת MATLAB. בנוסף, התייחסנו גם לשגיאת זמן התגובה, שהערכנו כ- $\delta t=\pu{0.3s}$. חשוב להעיר ששגיאה זו קְטֵנָה פי $10$ כי מדדנו $N=10$ מחזורים. 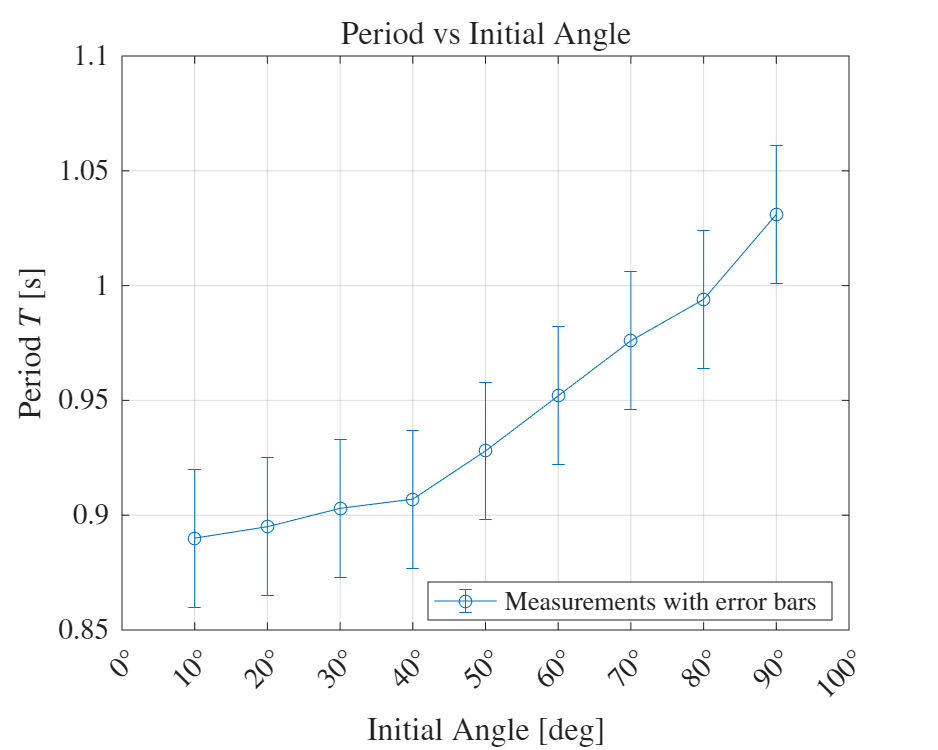![[degree-variation.png|bookhue|600]] >איור 3: זמן מחזור כתלות בזווית השחרור. ^[המקרא כאן צריך לכלול את הנקודות של המדידות ושל השגיאות בנפרד. כלומר, צריך להיות שני סימונים שונים, אחד לכל אחד] ניתן לראות מהגרף ^[אין שגיאה בזווית זה לא הגיוני] שעבור זוויות קטנות מ-$30^{\circ}$ השיפוע מתחיל להיות אופקי, ולכן השינוי בזמן המחזור בין זווית לזווית זניח. במילים אחרות, הנחת זוויות קטנות חלה עבור זוויות קטנות מ-$30^{\circ}$ ולכן נבחר בזווית זו כזווית השחרור בניסוי. <div><hr><hr></div> ## מהלך הניסוי עבור $10$ אורכי חוט שונים מ-$\pu{0.2m}$ עד $\pu{0.47m}$ בהפרשים של $\pu{0.03m}$, מדדנו את זמן המחזור הממוצע מתוך $10$ מחזורים לכל זווית. בעזרת MATLAB, חילקנו את הגדלים המתאימים בגדלים האופייניים שלהם (בחרנו בערך המקסימלי שהתקבל עבור כל אחד), ולקחנו את ה-$\ln$ שלהם. בנוסף, ביצענו רגרסיה לינארית על מנת לחשב את השיפוע של הגרף שהתקבל. כמו בגרף הקודם, התייחסנו גם לשגיאת הזמן תגובה. 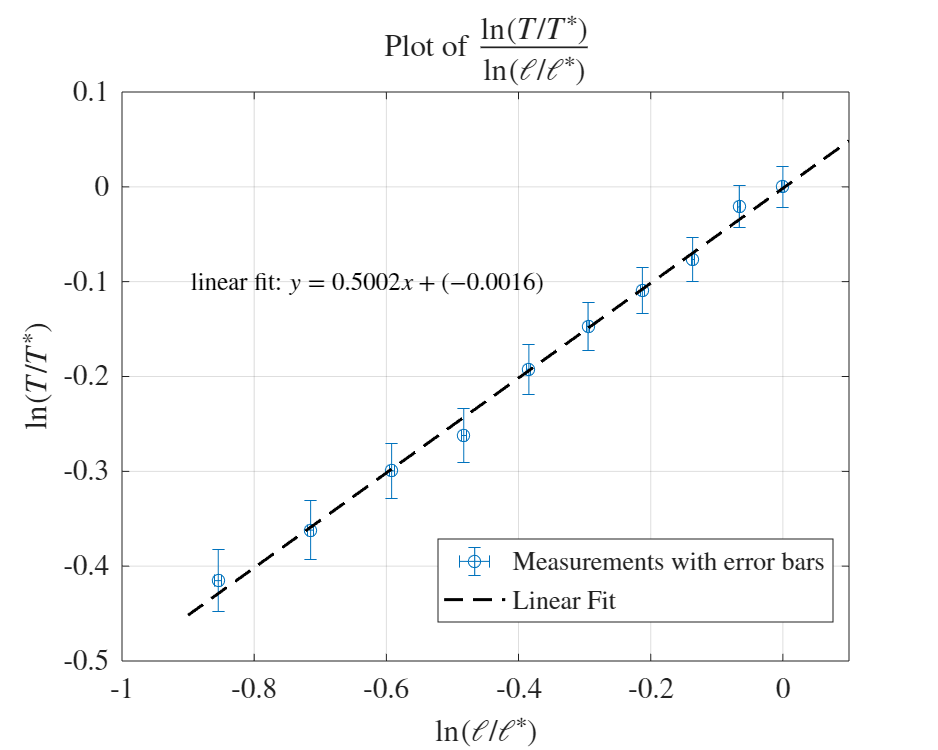התוצאות מוצגות בגרף הבא: ![[length-variation.png|bookhue]]^figure-linear-fit >איור 4: גרף של $\ln(T/T^{*})/\ln(\ell /\ell^{*})$, והרגרסיה הלינארית שלו. מהרגרסיה הלינארית קיבלנו מ-MATLAB קיבלנו: \alpha =0.500152\pm 0.026984
You can't use 'macro parameter character #' in math mode התוצאה קרובה מאוד לערך התאורטי ^[מה הוא הערך התאורטי?], מה שמאמת את החוק התאורטי של מטוטלת מתמטית. # דיון בתוצאות והשוואה לתאוריה במהלך הניסוי נבחנו הקשרים בין משתנים שונים בתנועת המטוטלת, ובפרט נבדק האם מתקיים הקשר התאורטי בין זמן המחזור לאורך החוט, בהתאם למשוואה $\text{(3)}$. על פי התאוריה, ערכו של $\alpha$ אמור להיות $0.5$. מניתוח [[#^figure-linear-fit|איור 4]] וקו הרגרסיה שהותאם באמצעות MATLAB, התקבלה המשוואה: \ln(T/T^{})=0.5002\ln(\ell /\ell^{ })-0.0016
You can't use 'macro parameter character #' in math mode ניתן לראות כי ערכו של $\alpha$ קרוב מאוד לערך התאורטי ($0.5$), עם שגיאה יחסית של כ-$0.04\%$ בלבד. בנוסף, טווח השגיאה שחושב בגרף כלל את הערך התאורטי - דבר המהווה אינדיקציה לחפיפה בין המודל לתוצאה הנמדדת. <div><hr><hr></div> ## ניתוח שגיאות למרות ההתאמה הכללית למודל התאורטי, קיימות מספר שגיאות שהשפיעו על תוצאת הניסוי: 1. **שגיאת מדידה אנושית**: תזמון שחרור המשקולת וספירת מחזורים נעשו ידנית על ידי סטודנט יחיד, דבר שהכניס עיכוב בזמן התגובה. 2. **שגיאת מכשירים**: חלק מהמדידות בוצעו באמצעות כלים לא מדויקים, לדוגמה: סרגל מדידה בעל דיוק של $1$ מ"מ ושעון עצר ידני, שתורמים לסטייה מצטברת במדידות האורך והזמן. 3. **הנחות לא אידאליות**: הניסוי התבסס על הנחות כמו חוט חסר מסה, תנועה במישור יחיד ומסה נקודתית, אולם בפועל המשקולת בעלת קוטר מסוים, החוט בעל מסה, והתנועה כללה גם סטיות קלות מהכיוון הראשי. כמו כן, חיכוך בציר ובאוויר גרם לדעיכת אנרגיה לאורך זמן. ## התורם המרכזי לשגיאה הגורם הדומיננטי לשגיאה הוא כנראה השגיאה האנושית בתזמון וזמן התגובה. סטייה של כמעט שנייה בזמני מחזור קצרי טווח יוצרת השפעה ניכרת על תוצאת הניסוי. ## דרכים לשיפור - שימוש בחיישנים אוטומטיים לזיהוי תנועת המטוטלת במקום תזמון ידני. - הגדלת מספר המחזורים בכל מדידה - דבר שמקטין את השפעת שגיאת הזמן על מחזור בודד. - הקטנת קוטר המשקולת כך שתתקרב יותר למסה נקודתית. - שימוש בכלי מדידה מדויקים יותר (מד זווית דיגיטלי, שעון עצר אוטומטי). # מסקנות מתוצאות הניסוי עולה כי קיים קשר לוגריתמי לינארי בין זמן המחזור של המטוטלת לאורך החוט, בהתאם למודל התאורטי (ראו משוואה $\text{(3)}$). בניתוח שביצענו נמצא כי מקדם השיפוע במשוואת הרגרסיה, אשר מייצג את $\alpha$, עמד על $0.5002$ עם טווח שגיאה של $[0.473169, 0.527136]$ ^[רושמים את זה כשגיאה של פלוס מינוס], דבר שתואם את הערך התאורטי של $0.5$. השגיאה היחסית עבור $\alpha$ הייתה קטנה מ-$0.04\%$, מה שמחזק את המסקנה שהתנהגות המערכת תואמת ^[מאששת] את המודל התאורטי. בנוסף, נמצא כי לזווית ההתחלתית של המטוטלת אין השפעה מהותית על זמן המחזור, כל עוד היא נשמרת בתחום של זוויות קטנות (פחות מ-$30^{\circ}$). עם זאת, סטיות קלות בתוצאות הורגשו כתוצאה משגיאות מדידה אנושיות, ובפרט בשל זמן תגובה לקוי, וכן ממגבלות כלי המדידה והנחות אידאליות שלא מתקיימות במלואן בפועל (כמו הנחה על מסה נקודתית וחוט חסר מסה). לו היו גורמים אלו מצומצמים באמצעים מדויקים יותר, סביר שתוצאות הניסוי היו מתקרבות אף יותר לערכים התאורטיים. # נספחים **חישוב השגיאה היחסית**: e_{\text{rel}} =\dfrac{\alpha-\alpha ^{*}}{\alpha }=\dfrac{0.5002-0.5}{0.5}=0.0004
You can't use 'macro parameter character #' in math mode # ביבליוגרפיה 1. "תדריך לניסוי הראשון מטוטלת מתמטית", אתר מודל טכניון. 2. "הנחיות לכתיבת דוח מעבדה" אתר מודל טכניון. 