LPH1_L003 מהירות רגעית

מספר קורס	01140032
מספר קבוצה	54
עמדת עבודה	23
שם מדריך	רז עמר
מגישים	עידו פנג בנטוב CLASSIFIED CLASSIFIED
תאריך	21/05/2025
דוח מסכם לניסוי	מהירות רגעית

---

---

מדידת מהירות רגעית ותאוצה של עגלה על מישור משופע

תקציר

בניסוי זה, נמדד מיקום עגלה הנעה על מסילת אוויר משופעת כפונקציה של הזמן. באמצעות נגזרות דיסקרטיות, חושבה המהירות הרגעית והתאוצה של העגלה. התוצאות הושוו לערכים תיאורטיים הנובעים מחוקי ניוטון, ונבחנה השפעת החיכוך במערכת. מטרת הניסוי היא למדוד את המהירות הרגעית, לקבוע את תאוצת העגלה, ולהעריך את מקדם החיכוך הקינטי בין העגלה למסילה.

מבוא

¹
מערכת הניסוי (ראו איור 1) מורכבת מעגלה הנעה על גבי מסילת אוויר משופעת. על העגלה מודפסים פסים שחורים במרווחים קבועים. שער פוטואלקטרי (חיישן קרוזה) מודד את זמן המעבר של הפסים דרכו, ומכך ניתן לחשב את מיקום העגלה כפונקציה של הזמן. העגלה משוחררת ממנוחה, מחליקה במורד המסילה, מתנגשת התנגשות אלסטית (בקירוב) בקצה המסילה (באמצעות גומייה), ונהדפת חזרה כך ששיא תנועתה (נקודת היפוך המהירות) מתרחש בתחום המדידה של השער הפוטואלקטרי.

איור 1: תרשים מערכת הניסוי. מסילת אוויר משופעת, עגלה עם פסים, שער פוטואלקטרי (חיישן קרוזה) המחובר למחשב, הגבהה בצד אחד, ואורך המסילה .

מהירות רגעית של גוף מוגדרת כנגזרת של פונקציית המיקום שלו, , לפי הזמן, :

מאחר ובניסוי מעשי לא ניתן למדוד את מיקום הגוף כפונקציה רציפה של הזמן, אלא בנקודות זמן בדידות במרווחים קבועים , נשתמש בקירוב נומרי לנגזרת. אחת השיטות הנפוצות היא שיטת ההפרשים המרכזיים:

כאשר הוא מיקום הגוף בזמן , ו- הוא פרמטר שלם חיובי הקובע את טווח המדידות המשמש לחישוב הנגזרת. חישוב התאוצה הרגעית יכול להתבצע באופן דומה מתוך סדרת ערכי המהירות, או ישירות מנתוני המיקום (ראו נספח א’).

תאוצת הגוף על מישור משופע בזווית ביחס לאופק, ללא חיכוך, נתונה על ידי:

(הסימן השלילי מציין תאוצה כלפי מטה אם הכיוון החיובי הוא מעלה). כאשר היא תאוצת הכובד, הוא גובה ההגבהה של קצה אחד של המסילה, ו- הוא אורך המסילה שלאורכו נמדד הפרש הגובה .

---

---

בנוכחות חיכוך קינטי, התאוצה הנמדדת בעלייה () והתאוצה הנמדדת בירידה () יושפעו מכוח החיכוך. מתוך תאוצות אלו, ניתן לחלץ את מקדם החיכוך הקינטי (נוסחאות מפורטות לתאוצות עם חיכוך מובאות בנספח א’):

כאשר , ו- ו- הן התאוצות הניסיוניות המתאימות.

תוצאות הניסוי

בתחילת הניסוי כיילנו את מסילת האוויר על ידי הנחת העגלה במרכז המסילה ושחרורה, כדי לוודא שהיא נמצאת בשיווי משקל ואינה מחליקה לכיוון מסוים. לאחר כיול זה, הגבהנו צד אחד של המסילה באמצעות משקולת מתכתית, ומדדנו את הפרמטרים הגיאומטריים של המערכת עבור גובה ואורך המסילה :

נמדד באמצעות סרגל וקליבר.

מספר הפסים על העגלה שנספרו על ידי החיישן (מתוך כיול ):

ערך תאוצת הכובד בו נעשה שימוש (ערך ידוע עבור חיפה):

נקבע מרחק שחרור אופטימלי של העגלה כך שתנועתה המלאה (ירידה, התנגשות, עלייה עד שיא גובה, וחזרה) תירשם היטב על ידי החיישן, ובפרט ששיא הגובה לאחר ההתנגשות יהיה בתחום המדידה.

בוצעו מספר הרצות של הניסוי, כאשר בכל פעם נרשמו נתוני מיקום העגלה כפונקציה של הזמן. נבדקו קצבי דגימה שונים של השער הפוטואלקטרי ( ו- במקרה זה) וגבהים שונים ().
הגרף הבא מציג את כל מדידות המיקום כפונקציה של הזמן, לאחר נרמול כל מקטע כך שיתחיל ב- ו-.

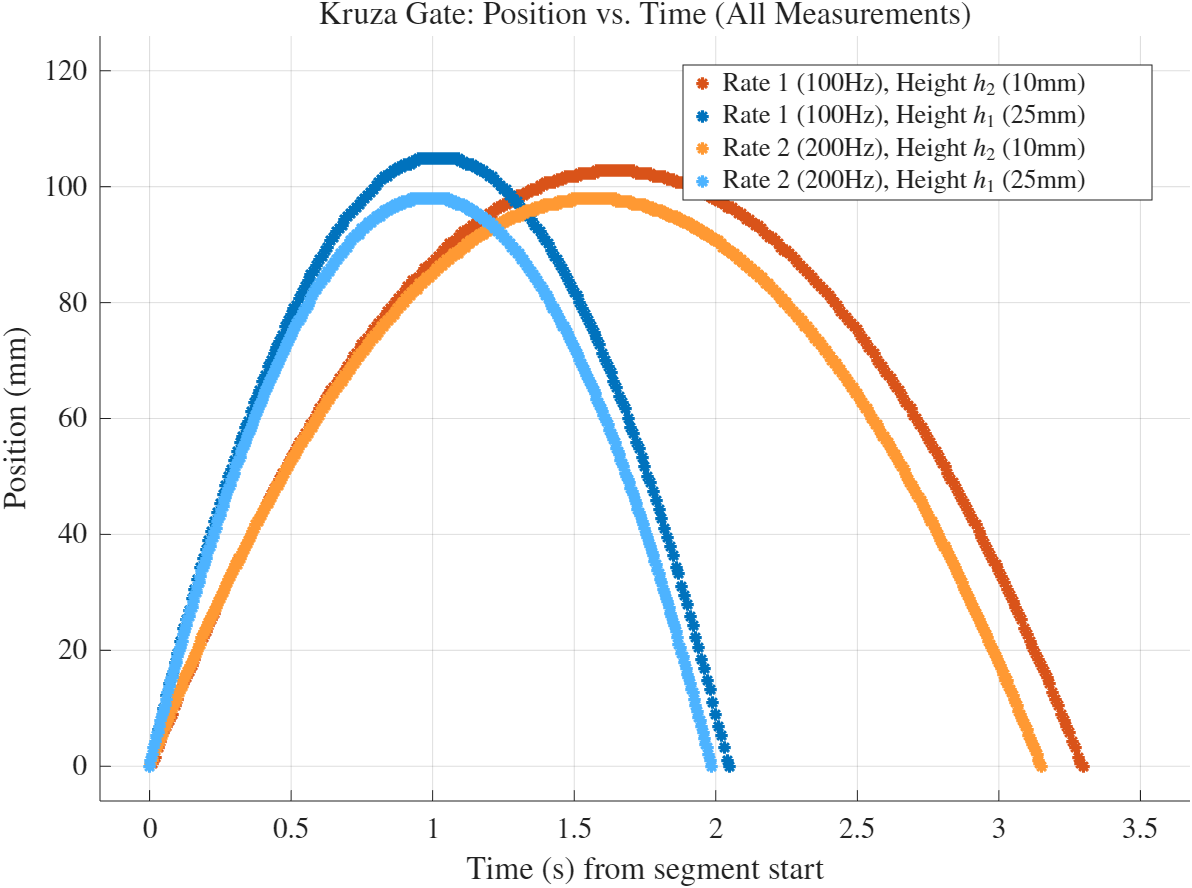
איור 2: מיקום העגלה כפונקציה של הזמן עבור כל המדידות. הצירים מנורמלים לתחילת כל מקטע תנועה.

באמצעות נוסחה (2), חושבה המהירות הרגעית של העגלה מתוך נתוני המיקום-זמן עבור המדידה בקצב דגימה וגובה . נבחנו ערכי עבור שיטת ההפרשים המרכזיים.

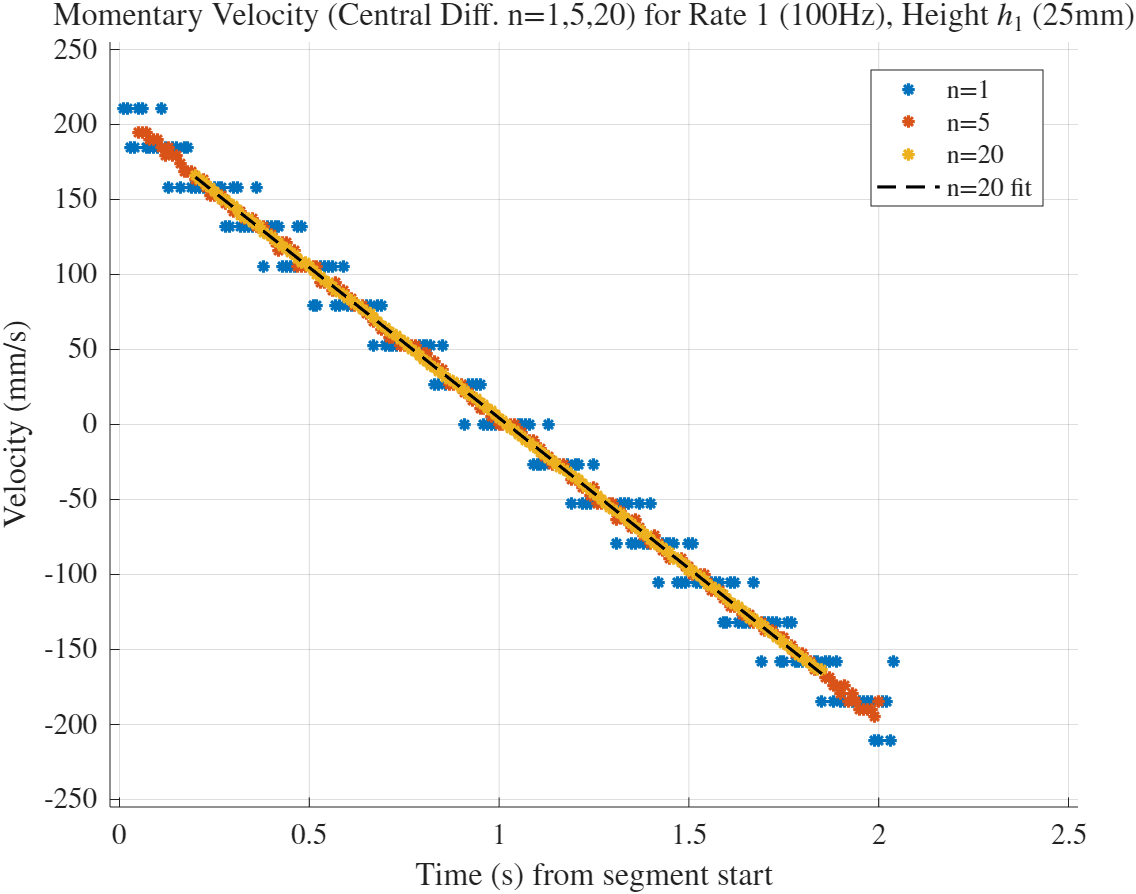
איור 3: מהירות העגלה () כפונקציה של הזמן (), כפי שחושבה באמצעות נגזרת דיסקרטית מרכזית עם . עבור ההתאמה הליניארית לנתוני , התקבל (ביחידות ו-), עם .

---

---

התאוצה עבור מדידה זו חושבה בשלוש דרכים:

1. מתוך התאמה פולינומית (ממעלה שנייה) לגרף המיקום:
   התאמת הפונקציה לנתוני המיקום-זמן באזור שיא הגובה, בנפרד למקטע העלייה ולמקטע הירידה.

   • מקטע עולה: התאוצה שהתקבלה מההתאמה היא .

   

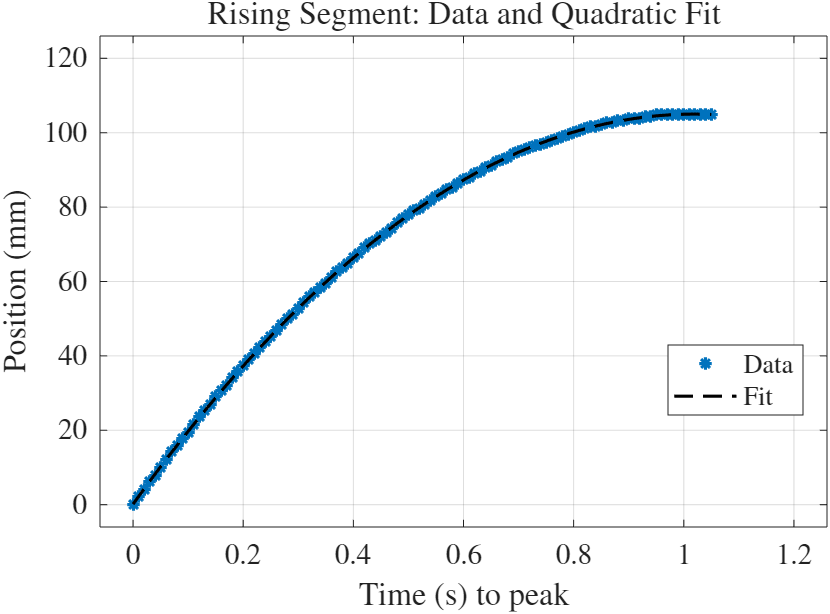
   איור 4: התאמה פרבולית למקטע העולה של התנועה.

   • מקטע יורד: התאוצה שהתקבלה מההתאמה היא .

   

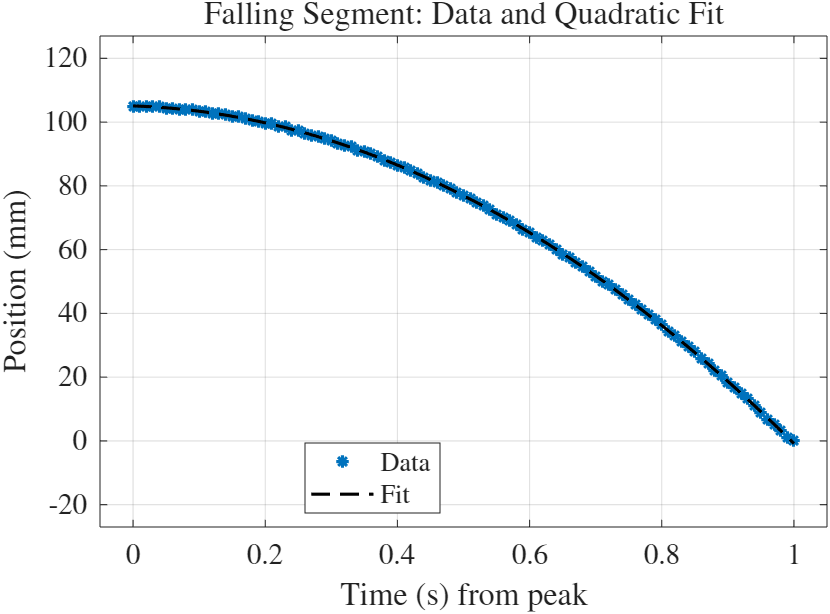
   איור 5: התאמה פרבולית למקטע היורד של התנועה.

2. מתוך רגרסיה לינארית לגרף המהירות (איור 3, עבור ):
   התאמת הפונקציה לנתוני המהירות-זמן עבור . שיפוע הגרף הוא התאוצה .

3. באמצעות נגזרת דיסקרטית שנייה של המיקום (נוסחה בנספח א’, עבור ):
   חישוב ישיר של התאוצה מנתוני המיקום. התאוצה הממוצעת שהתקבלה היא .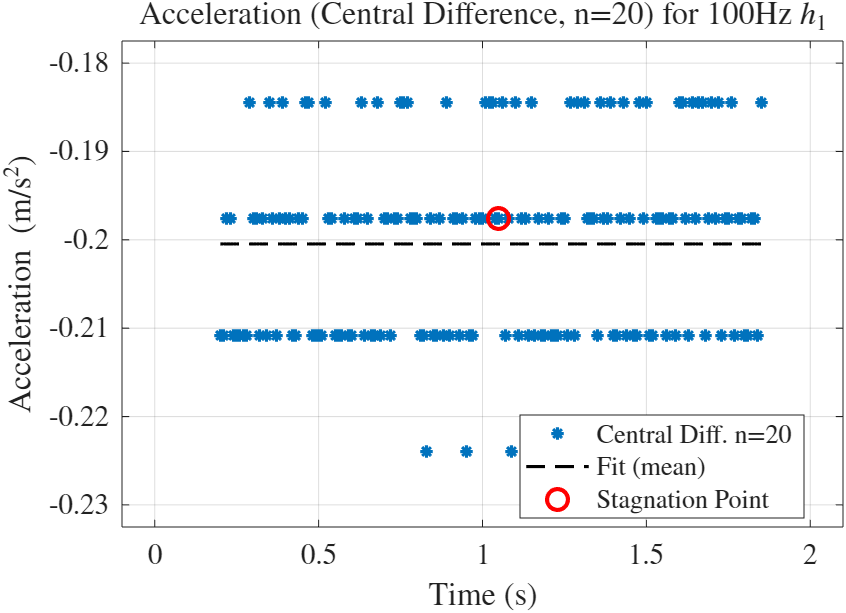

   

   איור 6: תאוצה כפונקציה של הזמן (הפרשים מרכזיים, ).

איור 4 ואיור 5 נותחו כדי להפריד בין קטע התנועה בעלייה לבין קטע התנועה בירידה. לכל קטע חושבה התאוצה בנפרד ( ו-) באמצעות התאמות פולינומיות למקטעי המיקום המתאימים (כפי שפורט בסעיף הקודם עבור מדידה בקצב ).
הערכים שהתקבלו הם:

• בקטע העלייה:
• בקטע הירידה:
  באמצעות נוסחה (4) וערכי התאוצות הללו, וכן ערכי , חושב מקדם החיכוך הקינטי והתקבל (השגיאה ב- חושבה בנספח ג’).

דיון בתוצאות והשוואה לתאוריה

בסעיף זה נדון במשמעות התוצאות שהתקבלו ובהשוואתן למודל התיאורטי.
ראשית, נשווה את ערכי התאוצה שהתקבלו בשיטות השונות (). יש לבדוק את העקביות ביניהם ואת טווח השגיאה של כל מדידה. לדוגמה, עבור המדידה עם גובה (בקצב דגימה של ), הערכים הם:

התאוצה התיאורטית, בהנחה של היעדר חיכוך (נוסחה (3)), עבור הערכים ו- וערך תאוצת הכובד :

(השגיאה ב- חושבה בנספח ג’).

הערכים המדודים עקביים זה עם זה בטווח השגיאות שלהם. ממוצע (לא משוקלל) של ארבע התאוצות הניסיוניות הוא ². ערך זה קרוב יחסית לערך התיאורטי אך מעט גבוה יותר, גם כאשר לוקחים בחשבון את שגיאת המדידה. הפער יכול להיות מוסבר בחלקו על ידי נוכחות חיכוך (שצפוי להקטין את גודל התאוצה בירידה ולהגדיל את גודל ההאטה בעלייה), או שגיאות מדידה אחרות שלא נלקחו בחשבון במלואן.

ערך מקדם החיכוך הקינטי שחושב, , הוא ערך נמוך מאוד, כצפוי ממערכת עם מסילת אוויר. העובדה ש מאששת את קיום החיכוך המתנגד לתנועה.

הבחירה בערך לחישוב הנגזרת הדיסקרטית היא בעלת חשיבות. ערך קטן מדי (למשל ) עלול להגביר את השפעת הרעש במדידות המיקום, בעוד ערך גדול מדי מחליק את הנגזרת על פני מקטע זמן רחב יותר, ובכך מרחיק אותה מההגדרה של ערך “רגעי” ועלול “לפספס” שינויים מהירים. הבחירה ב- עבור חישוב המהירות והתאוצה מנתונים בדידים נראית כפשרה טובה עבור הנתונים הנוכחיים.

מקורות שגיאה אפשריים וניתוחם:

1. שגיאות מדידה במכשור:
   • אי-דיוק במדידת ו-. שגיאה זו משפיעה ישירות על חישוב ועל התאוצה התיאורטית.
   • שגיאה בקביעת (אף כי ערך זה לרוב מדויק למדי).
   • דיוק החיישן הפוטואלקטרי: תלוי ברזולוציית הפסים על העגלה ובדיוק מדידת הזמן .
2. שגיאות שיטתיות:
   • חיכוך שיורי במסילה: למרות השימוש במסילת אוויר, קיים חיכוך קטן אך משמעותי.
   • התנגדות אוויר: לרוב זניחה במהירויות הנמוכות בניסוי זה, אך קיימת.
   • איזון המסילה: אם המסילה אינה מאוזנת באופן מושלם (בנוסף לשיפוע הרצוי לאורכה), הדבר עלול להשפיע על התנועה.
3. שגיאות אקראיות: תנודות קטנות במהירות שחרור העגלה, רעידות בסביבה המשפיעות על המדידה.
4. קירובים במודל המתמטי:
   • הנגזרת הדיסקרטית היא קירוב לנגזרת הרציפה. השגיאה בקירוב זה תלויה ב- ובסדר הקירוב.

מסקנות

בניסוי זה נחקרה תנועת עגלה על מישור משופע, ונמדדה המהירות הרגעית והתאוצה שלה.

1. התאוצה הקבועה (בקירוב) של העגלה עבור המדידה עם גובה (בקצב דגימה של ) חושבה באמצעות מספר שיטות, והתקבלו ערכים עקביים זה עם זה. ממוצע התאוצות הניסיוניות הוא (השגיאה היא ממוצע השגיאות האינדיבידואליות).
2. הערך המדוד של התאוצה היה קרוב לערך התיאורטי הצפוי ללא חיכוך (). הפער הקטן מוסבר, ככל הנראה, על ידי שילוב של חיכוך שיורי ושגיאות מדידה.
3. מקדם החיכוך הקינטי בין העגלה למסילה חושב על סמך ההבדל בין התאוצות בעלייה ובירידה, ונמצא ערך קטן, , התואם את הציפייה ממערכת עם מסילת אוויר.
4. שיטת הנגזרת הדיסקרטית המרכזית, עם בחירה של פרמטר החישוב , הוכחה ככלי יעיל ואמין לחישוב מהירות ותאוצה רגעיות מנתונים בדידים המתקבלים מחיישן מיקום.
5. הניסוי הדגים בהצלחה את עקרונות התנועה שוות התאוצה (בקירוב) תחת השפעת כוח הכובד והחיכוך, ואפשר אימות של המודלים התיאורטיים המתארים תנועה זו.

---

---

נספחים

בנספחים הבאים מפורטים פיתוחים וחישובים נוספים, כולל ניתוח שגיאות כמותי עבור הגדלים המרכזיים.

נספח א’: פיתוחים ונוסחאות משלימות

חישוב נומרי של תאוצה:
התאוצה הרגעית, , ניתנת לחישוב כנגזרת הדיסקרטית של המהירות (שחושבה בנוסחה 2 במבוא):

לחילופין, ניתן לחשב את התאוצה ישירות מהמיקום באמצעות נגזרת דיסקרטית שנייה:

תאוצות עם חיכוך קינטי:
כאשר קיים חיכוך קינטי (עם מקדם ), התאוצות בעלייה () ובירידה (), כאשר התנועה היא לאורך ציר ה- המקביל למסילה והכיוון החיובי הוא במעלה המסילה, הן:

מנוסחאות אלו, בשילוב עם התאוצות הניסיוניות ו-, ניתן לחלץ את מקדם החיכוך הקינטי כפי שמופיע בנוסחה (4) במבוא.

נספח ב’: דוגמאות לחישובים מנתוני הניסוי

חישוב מתוך התאמה פולינומית:
מתוך התאמה פרבולית למקטע העולה של המדידה עם גובה (בקצב דגימה של ), .
התאוצה היא .
לדוגמה, עבור התאמה (לאחר המרה ליחידות SI והתאמה לזמן שמתחיל ב- למקטע):

באופן דומה עבור המקטע היורד, עם התאמה , נקבל:

חישובים עבור מקדם החיכוך :
בהינתן ערכי המערכת ותאוצות נמדדות

וכן :
חישוב :

חישוב :

חישוב באמצעות נוסחה (4):

נספח ג’: חישוב שגיאות

בנספח זה מפורט חישוב השגיאות עבור התאוצה התיאורטית ומקדם החיכוך הקינטי .

שגיאה בתאוצה התיאורטית :
התאוצה התיאורטית נתונה על ידי .
בהנחה שהשגיאות ב- הן בלתי תלויות, השגיאה היחסית בריבוע היא:

מכאן, השגיאה המוחלטת היא:

עם הערכים הנתונים ו-, נקבל:

לכן, .

שגיאה במקדם החיכוך הקינטי :
מקדם החיכוך נתון על ידי .
נסמן . השגיאה ב- היא .
השגיאה ב- יותר מורכבת, אך מכיוון ש- קטנה מאוד, , והשגיאה בו זניחה יחסית לשגיאה האחרות. כמו כן, נניח שהשגיאה ב- זניחה יחסית לשגיאה ב-.
לכן, בקירוב:

מאחר והשגיאות ב- וב- קטנות מאוד יחסית, נתמקד בשגיאה הנגררת מ- בלבד:

מהצבת הערכים הנתונים:

לכן, .

ביבליוגרפיה

1. “תדריך מהירות רגעית של עגלה במישור משופע”, אתר “מודל טכניון”
2. “הנחיות לכתיבת דוח מעבדה”, אתר מודל טכניון

הערות שוליים

1. המבוא רשום בצורה מעולה לגמרי, רק חסר יחידות ליד כל פרמטר מתחת לנוסחאות ↩

2. היית צריך להראות את השגיאה היחסית של כל תאוצה שנמדדה לעומת התאוצה המתקבלת מהתאוריה ולא ערך של הממוצע שלהם ↩