תרגיל בית 6
| סטודנט א’ | סטודנט ב’ | |
|---|---|---|
| שם | עידו פנג בנטוב | ניר קרל |
| ת”ז | CLASSIFIED | CLASSIFIED |
| דואר אלקטרוני | CLASSIFIED | CLASSIFIED |
שאלה 1
שאלה א’
סעיף ב’
האינטגרנד שלנו:
נשים לב כי:
וערכי הפונקציה בנקודות אלו:
ניוטון-קוטס מסדר ראשון:
נציב:
ניוטון-קוטס מסדר שני:
נציב:
השגיאה בפועל:
השגיאה התאורטית:
כאשר
נמצא את הנגזרות של
הפונקציות
נסיק כי החסמים העליונים והתחתונים עבור שתי השיטות הן:
אכן השגיאות שלנו נמצאים בטווח של השגיאה התאורטית.
סעיפים ג’, ד ו-ה’
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
def composite_trapezoidal(f, a, b, n):
h = (b - a) / n
s = f(a) + f(b)
for i in range(1, n):
s += 2 * f(a + i * h)
return s * h / 2
def composite_simpsons(f, a, b, n):
h = (b - a) / n
s = f(a) + f(b)
for i in range(1, n):
if i % 2 == 0:
s += 2 * f(a + i * h)
else:
s += 4 * f(a + i * h)
return s * h / 3
def richardson_extrapolation_simp(f, a, b, n):
I1 = composite_simpsons(f, a, b, n)
I2 = composite_simpsons(f, a, b, 2*n)
return (16*I2 - I1) / 15
f = lambda x: (x+1)/(4*x+3)
a = 0
b = 6
points = [21,41,81,161]
n = np.array(points) - 1
n_richardson = n[1:]//2
x = sp.symbols('x')
fsym = (x+1)/(4*x+3)
I_real = sp.integrate(fsym, (x, 0, 6))
I_real = float(I_real)
E_trap = [abs(I_real - composite_trapezoidal(f, a, b, i)) for i in n]
E_simp = [abs(I_real - composite_simpsons(f, a, b, i)) for i in n]
E_rich = [abs(I_real - richardson_extrapolation_simp(f, a, b, i)) for i in n_richardson]
print("n | Trapezoidal | Simpson's | Richardson")
for i in range(len(n)):
E_rich_value = E_rich[i-1] if i >= 1 else '---'
print(f"{n[i]} | {E_trap[i]:.6e} | {E_simp[i]:.6e} | {E_rich_value if isinstance(E_rich_value, str) else f'{E_rich_value:.6e}'}")
plt.plot(n, E_trap, 'o-', label="Trapezoidal rule")
plt.plot(n, E_simp, 'o-', label="Simpson's rule")
plt.plot(n_richardson*2, E_rich, 'o-', label="Richardson extrapolation (Simpson's)")
for i, txt in enumerate(n):
plt.annotate(txt, (n[i], E_trap[i]), textcoords="offset points", xytext=(0,-15), ha='center')
log_n = np.log(n)
log_n_richardson = np.log(n_richardson*2)
log_E_trap = np.log(E_trap)
log_E_simp = np.log(E_simp)
log_E_rich = np.log(E_rich)
slope_trap, _ = np.polyfit(log_n, log_E_trap, 1)
slope_simp, _ = np.polyfit(log_n, log_E_simp, 1)
slope_rich, _ = np.polyfit(log_n_richardson, log_E_rich, 1)
print(f"Slope of Trapezoidal rule: {slope_trap}")
print(f"Slope of Simpson's rule: {slope_simp}")
print(f"Slope of Richardson extrapolation (Simpson's): {slope_rich}")
plt.yscale('log')
plt.xscale('log')
plt.title('Error vs n')
plt.xlabel('n')
plt.ylabel('Error')
plt.grid(True, which="both", ls="--", alpha=0.5)
plt.legend()
plt.show()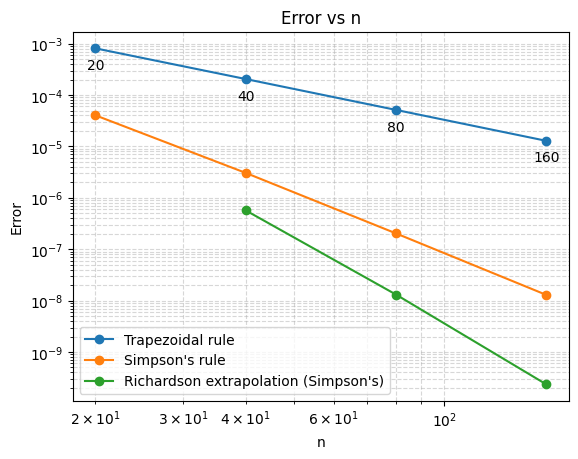
שגיאה אמיתית ביחס ל-
, לפי כל שיטה.
פלט הקוד:
n | Trapezoidal | Simpson's | Richardson
20 | 8.105947e-04 | 4.039358e-05 | ---
40 | 2.049434e-04 | 3.059592e-06 | 5.706596e-07
80 | 5.138850e-05 | 2.035455e-07 | 1.314238e-08
160 | 1.285683e-05 | 1.294218e-08 | 2.352962e-10
Slope of Trapezoidal rule: -1.9930828748445153
Slope of Simpson's rule: -3.8733404175488584
Slope of Richardson extrapolation (Simpson's): -5.621968240212317
נראה כי התוצאות שלנו תואמות לתאוריה.
מההרצאה, השגיאה של שיטת הטרפזים ושיטת סימפסון המוכללים:
מספר הקטעים
נסמן:
ולכן:
עבור המשוואה הראשונה:
באותו אופן עבור המשוואה השניה:
נסיק כי השיפועים המתקבלים הם:
ואכן ניתן לראות בגרף ומהטבלה כי השיפוע המתקבל הוא
עבור אקסטרפולציית ריצ’רדסון, אנו רואים מהגרף ומהטבלה כי יש לו שיפוע יותר חד:
בדיוק כמצופה מהתאוריה, בה ראינו כי אקסטרפולציית ריצ’רדסון על שיטת סימפסון מקטינה את סדר הגודל של השגיאה, שהיה
תרגיל 2
סעיף א’
נשתמש בשיטת המקדמים החופשיים:
נקבל את מערכת המשוואות:
נפתור:
ולכן:
סעיף ב’
נציב בקירוב:
סעיף ג’
בקטע
תרגיל 3
סעיף א’
סעיף ב’
עבור 2 צמתי אינטגרציה:
ולכן השגיאה שלנו:
עבור 3 צמתי אינטגרציה:
ולכן השגיאה שלנו:
סעיף ג’
נעביר לתחום אינטגרציה
נציב בנוסחה של אינטגרציית גאוס:
נסמן:
ולכן:
מטבלת שורשי לז’נדר:
נוכל כעת לשער את ערך האינטגרל:
נסיק כי השגיאה:
נשים לב שבסעיף ב’ קיבלנו חסם שלילי, כלומר בשיטה מסעיף ב’ קיבלנו שטח קטן מהשטח האמיתי. לעומת זאת בשיטה בסעיף זה החסם הוא חיובי, כלומר תמיד נקבל שטח גדול מהשטח האמיתי.
נבדוק את השגיאה התיאורטית לפי שיטת גאוס-לז’נדר. עבור
נשים לב שהנגזרת הרביעית היא:
ולכן החסם העליון והתחתון הם:
קיבלנו ש-
סעיף ד’
מסעיף קודם:
שורשי לז’נדר:
נוכל כעת לשער את ערך האינטגרל:
נסיק כי השגיאה:
נשים לב שבסעיף ב’ קיבלנו חסם שלילי, כלומר בשיטה מסעיף ב’ קיבלנו שטח קטן מהשטח האמיתי. לעומת זאת בשיטה בסעיף זה החסם הוא חיובי, כלומר תמיד נקבל שטח גדול מהשטח האמיתי.
נבדוק את השגיאה התיאורטית לפי שיטת גאוס-לז’נדר. עבור
נשים לב שהנגזרת הרביעית היא:
ולכן החסם העליון והתחתון הם:
קיבלנו ש-
תרגיל 4
נפרק את האינטגרל לשני חלקים חצי אינסופיים:
מאחר והאינטגרנד הנתון זוגי, נוכל פשוט לחשב
(כי
נפרק את
נרצה לחסום את השגיאה הכוללת ב-
נציב את ה-
נבחר
נחשב את הנגזרת השנייה:
לנגזרת השנייה ערך מקסימלי בערך מוחלט ב-
נציב בנוסחה לשגיאה:
נבחר
החישוב ב-python:
from math import pi, sqrt
L = 6
h = 0.04
n = int(L/h)
f = lambda x: 1/(1+x**4)
sum = f(0) + f(L)
for i in range(1, n):
sum += 2*f(h*i)
sum *= h/2
I = 2*sum
true_I = pi/sqrt(2)
print(f"The integral from 0 to 6 is: {sum}")
print(f"The integral from -6 to 6 is: {I}")
print(f"The true value is: {true_I}")
print(f"The absolute error is: {abs(true_I - 2*sum)}")נקבל בפלט:
The integral from 0 to 6 is: 1.109177966253471
The integral from -6 to 6 is: 2.218355932506942
The true value is: 2.221441469079183
The absolute error is: 0.0030855365722408656
הפתרון שלנו:
והשגיאה:
אכן הגענו לשגיאה קטנה מ-
