THE1_006 אנטרופיה

→ קודם: THE1_005הבא: THE1_007 ←

אנטרופיה - תכונת מערכת

הגדרת השינוי באנטרופיה

ניזכר כי תכונת מערכת לא תלויה בתהליך בין שני מצבים, אלא רק במצבים עצמם.
נניח וישנם שני מחזורים הפיכים המתבצעים במערכת סגורה כמתואר באיור:

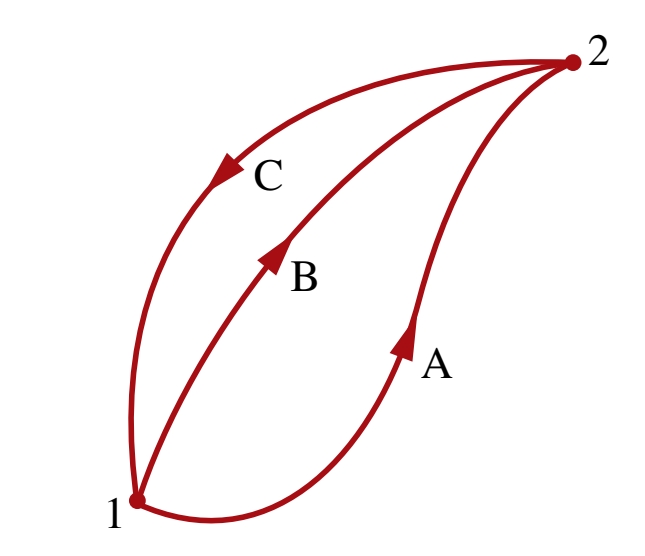
מחזור אחד מכיל את תהליך ו-, והתהליך השני מכיל את תהליך ו-.

מאי שוויון קלאוזיוס, עבור המחזור הראשון, מאחר והוא הפיך:

עבור המחזור השני:

נחסר בין שתי המשוואות ונקבל:

קיבלנו כי האינטגרל של נשאר אותו הדבר לשני התהליכים. מאחר ו- ו- הם כלליים, נסיק כי האינטגרל על הוא אותו הדבר לכל תהליך הפיך בין שני מצבים. לפיכך, קיבלנו כאן תכונת מערכת, שנקרא לה אנטרופיה.

הגדרה:

השינוי באנטרופיה הוא:

כאשר הסימון נועד כדי להדגיש שהאינטגרל מחושב על תהליך תהליך הפיך פנימית.

מבחינה דיפרנציאלית, נוכל לרשום את השינוי באנטרופיה:

הערות:

1. אנטרופיה היא תכונה אקסטנסיבית, ולכן נוכל להגדיר לה גם אנטרופיה סגולית:

2. היחידות של אנטרופיה הן:

חישוב האנטרופיה

מאחר ואנטרופיה היא תכונה, השינוי באנטרופיה של מערכת ממצב אחד למצב שני הוא זהה עבור כל התהליכים, בין אם הם הפיכים או בלתי הפיכים, בין שני המצבים.

מההגדרה לשינוי באנטרופיה, נוכל לחשב את האנטרופיה יחסית למצב רפרנס כלשהו (כמו שעושים עבור ו-). הערך של האנטרופיה במצב יחסית לערך שלה במצב ניתן לחישוב ע”י:

שוב, הסימון נועד כדי להדגיש כי החישוב של האינטגרל הוא אך ורק על תהליך הפיך. עבור תהליך שהוא לא בהכרח הפיך, מתקיים אי השוויון הבא (שימו לב, אין את הסימון ):

כאשר השוויון מתקיים רק אם האינטגרל מחושב על תהליך הפיך.

משוואות אנטרופיה

מאחר והשינוי באנטרופיה בין שני מצבים נקבע ע”י המשוואה:

נוכל לרוב לחשב אותה ע”י משוואות שנפתח כעת. משוואות שנקראות גם משוואות אנטרופיה, מאפשרים לחשב שינויי אנטרופיה מנתונים שלרוב יש לנו כבר, כמו וכו’.

תהי מערכת דחיסה פשוטה העוברת תהליך הפיך. לפי חוק ראשון:

מאחר והתהליך הפיך, מתקיים:

אם נשנה טיפה את ההצגה הדיפרנציאלית הגדרת השינוי באנטרופיה, נקבל:

נציב בחוק ראשון ונקבל את משוואות האנטרופיה הראשונה.

אם נציב את הגדרת האנתלפיה, , ונבצע את הדיפרנציאל:

אז נקבל את משוואת האנטרופיה השנייה:

נוכל גם לרשום את שתי המשוואות בצורה הסגולית שלהן:

שינוי אנטרופיה של גז אידיאלי

ניזכר כי עבור גז אידיאלי, מתקיים:

אם נציב את משוואות האנטרופיה, נקבל את הקשרים הבאים:

לאחר אינטגרציה, וההנחה ש- ו- קבועים:

שינוי אנטרופיה בתהליך הפיך במערכת סגורה

במערכת סגורה העבורת תהליך הפיך פנימי, האנטרופיה יכולה לרדת, לעלות, או להישאר קבועה. ניתן לראות זאת מ:

המראה כי כאשר מערכת סגורה העוברת תהליך הפיך פנימית מקבלת אנרגיה דרך מעבר חום, אנטרופיית המערכת עולה. נוכל לומר כי מעבר אנטרופיה מלווה את מעבר החום. הכיוון של מעבר האנטרופיה זהה לכיוון מעבר האנרגיה. בתהליך אדיאבטי הפיך פנימית, ולכן האנטרופיה נשארת קבועה. לתהליך כזה אנו קוראים תהליך איזנטרופי.

מעבר חום כשטח של גרף

אם נבצע אינטגרל על ההצגה הדיפרנציאלית של שינוי אנטרופיה, נקבל:

נסיק מכך שהמעבר חום של מערכת סגורה בזמן תהליך הפיך פנימית ניתנת להצגה כהשטח של גרף טמפרטורה-אנטרופיה:

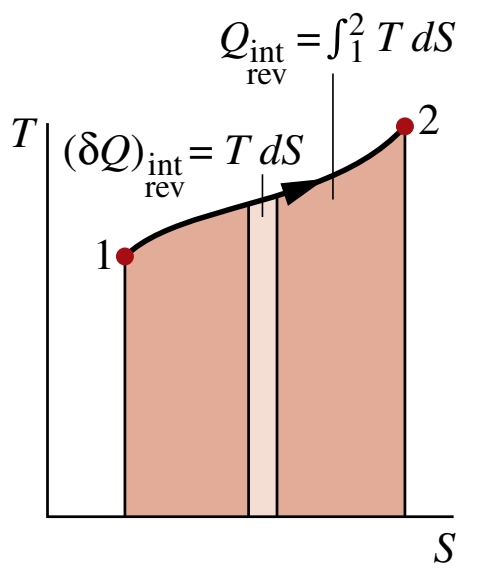
נשים לב שהטמפרטורה חייב להיות מוצגת בסקאלת קלוין. בנוסף, שטח הגרף לא ייצג את מעבר החום אם מדובר בתהליך בלתי הפיך.

דוגמה:

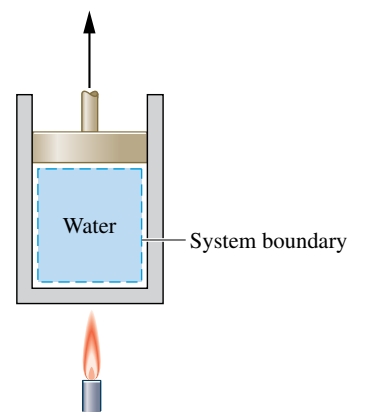
מים במצב נוזלי רווי ב-, נמצא במערכת צילינדר-בוכנה. המים עוברים תהליך למצב אד רווי, כאשר הבוכנה חופשיה לזוז בצילינדר. אם השינוי של המצב של המצב נוצר כתוצאה מחימום המים כאשר הוא עובר תהליך הפיך פנימית בלחץ וטמפרטורה קובעים, מצאו את אינטראקציית העבודה והחום הסגולית.

פתרון:

בתהליך בלחץ קבוע, העבודה הסגולית היא:

מטבלאות קיטור נוכל להציב את הנתונים:

מאחר והתהליך הפיך פנימית ובטמפרטורה קבועה, נסיק כי:

ולכן החום הסגולי:

מערכי הטבלאות קיטור, נמצא כי:

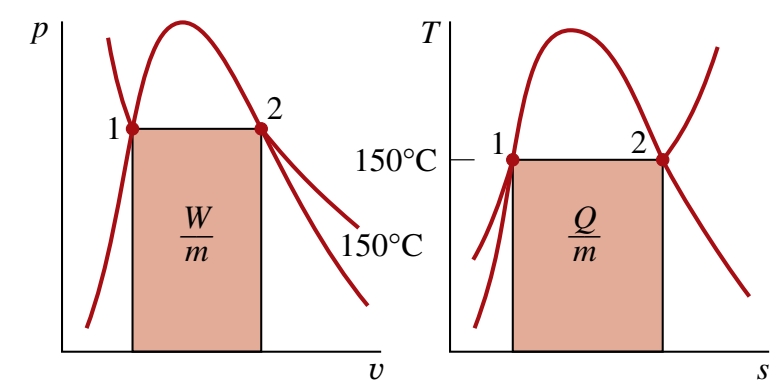
נוכל להציג את החישובים האילו גם על דיאגרמות עבור חום ו- עבור העבודה:

מאזן אנטרופיה במערכות סגורות

מאזן האנטרופיה הוא ביטוי לחוק שני. עבור מערכות סגורות:

כאשר הסימון מדגיש כי מחשבים את האינטגרל בגבולות המערכת.

לפעמים נרצה לרשום את מאזן האנטרופיה בצורתו הדיפרנציאלית:

משמעות מאזן האנטרופיה

אם המצבים הסופיים קבועים, אז צד שמאל של מאזן האנטרופיה ניתנים לחישוב ללא תלות בתהליך. לעומת זאת, שני הביטויים בצד ימין תלויים בתהליך ולא ניתנים לחישוב רק ע”י שני המצבי קיצון.

הביטוי הראשון בצד ימין, , קשור למעבר החום אל או מהמערכת במהלך התהליך. נקרא לביטוי זה מעבר האנטרופיה המלווה מעבר חום. הכיוון של האנטרופיה הוא באותו כיוון של המעבר חום, ולכן הסימנים שלהם זהים. סימן חיובי משמעו על שהאנטרופיה עברה לתוך המערכת, וסימן שלילי משמעו שהאנטרופיה עברה מהמערכת. כאשר אין מעבר חום, כלומר כשהתהליך הוא אדיאבטי, אין מעבר אנטרופיה.

הביטוי השני בצד ימין, , חיובי כאשר ישנם תהליכים בלתי הפיכים בתוך התהליך, ונעלם כאשר התהליך הוא הפיך פנימית. ניתן לחשוב על ביטוי זה כהאנטרופיה שנוצרה בתוך המערכת ע”י התהליכים הלא הפיכים בה. נסיק כי:

הערך של היווצרות אנטרופיה לא יכול להיות שלילי. לעומת זאת, השינוי באנטרופיה של מערכת יכול להיות חיובי, שלילי, או אפס:

כיווניות תהליכים

עיקרון גדילת האנטרופיה

עבור מערכת מבודדת, מאחר ואין שום מעברי אנרגיה בגבולותיה, לפי חוק ראשון, מתקיים:

לכן, האנרגיה של מערכת מבודדת נשארת קבועה. מאחר ואנרגיה היא תכונה אקסטנסיבית, הערך שלה עבור מערכת מבודדת היא הסכום של המערכת וסביבתה:

כדי שהתהליך יתרחש, נדרש שסכום האנרגיה של המערכת וסביבתה יישאר קבוע. אבל, לא כל התהליכים יכולים להתקיים גם אם תנאי זה מתקיים. ישנו עוד תנאי - התהליכים חייבים לקיים את חוק שני. מאזן האנטרופיה עבור מערכות מבודדות:

או:

כאשר הוא כלל האנטרופיה שנוצרה במערכת וסביבתה (לפעמים מסמנים במקום ).
קיבלנו כי בכל התהליכים המציאותיים נוצרת תמיד אנטרופיה, מה שמוביל למסקנה שהאנטרופיה של היקום תמיד גודלת - עיקרון זה נקרא עיקרון גדילת האנטרופיה, והוא לרוב נחשב כנוסח שקול לחוק שני.

כיוון שאנטרופיה היא תכונה אקסטנסיבית, הערך שלה עבור מערכת מבודדת היא הסכום של ערכיה עבור המערכת וסביבתה:

נשים לב שמשוואה זו לא דורשת ששינוי האנטרופיה יהיה חיובי עבור המערכת וחיובי עבור הסביבה, אלא רק שסכומם יהיה חיובי.

טיפים:

1. כאשר שואלים האם תהליך מסוים אפשרי, עלינו לבדוק שני דברים: חוק ראשון, וחוק שני. בדרך כלל, כאשר נבדוק את חוק ראשון, נקבל תנאי כלשהו על המערכת. נציב את תנאי זה בחוק שני (למשל, נדרוש שהנצילות לא יותר גדולה מנצילות קרנו), ונראה אם אנו מקבלים סתירה.
2. כאשר אנו רוצים לבדוק האם חוק שני מתקיים בעזרת עיקרון גדילת האנטרופיה, יהיה לנו מאוד נוח להסתכל מנקודת מבט של הסביבה. אנו מניחים שבסביבה אין שום ייצור אנטרופיה, ולכן אנו יכולים לחשב את השינוי באנטרופיה פשוט כסכום של המעברי חום, , בלי איבר מעצבן שעבור המערכת עצמה אנו לא בהכרח יודעים מהו.

תהליכים איזנטרופיים

נזכיר כי תהליך איזנטרופי הוא תהליך בו האנטרופיה קבועה. בנוסף ראינו כי כאשר התהליך הוא אדיאבטי והפיך פנימית (קוואזיסטטי), אז התהליך הוא איזנטרופי. מכך נקבל את השילוש הקדוש:

הגרף הנ”ל מתאר את הקשר בין תהליכים הפיכים, אדיאבטיים ואיזנטרופיים. כדי שתהליך יהיה אחד מהסוגים האלה, הוא צריך להיות גם שני הסוגים האחרים. כך למשל, אם תהליך הוא איזנטרופי ואדיאבטי, אז הוא גם הפיך פנימית.

שימוש במודל הגזים האידיאליים

נרשום את עיקרון גדילת האנטרופיה בצורתה הסגולית:

לכן לפי שינוי אנטרופיה של גז אידיאלי, עבור גזים אידיאליים, נוכל לרשום:

לפי חוקי לוגריתמים, נכניס לאותו ה- ונעלה את בחזקה:

ונקבל ש:

אם התהליך אדיאבטי, והפיך פנימית (קוואזיסטטי), אז התהליך הוא איזנטרופי, כלומר . במקרה זה נקבל את השוויון:

ובכך הוכחנו את המשוואות עבור תהליך תהליך פוליטרופי אדיאבטי וקוואזיסטטי, כך ש- .

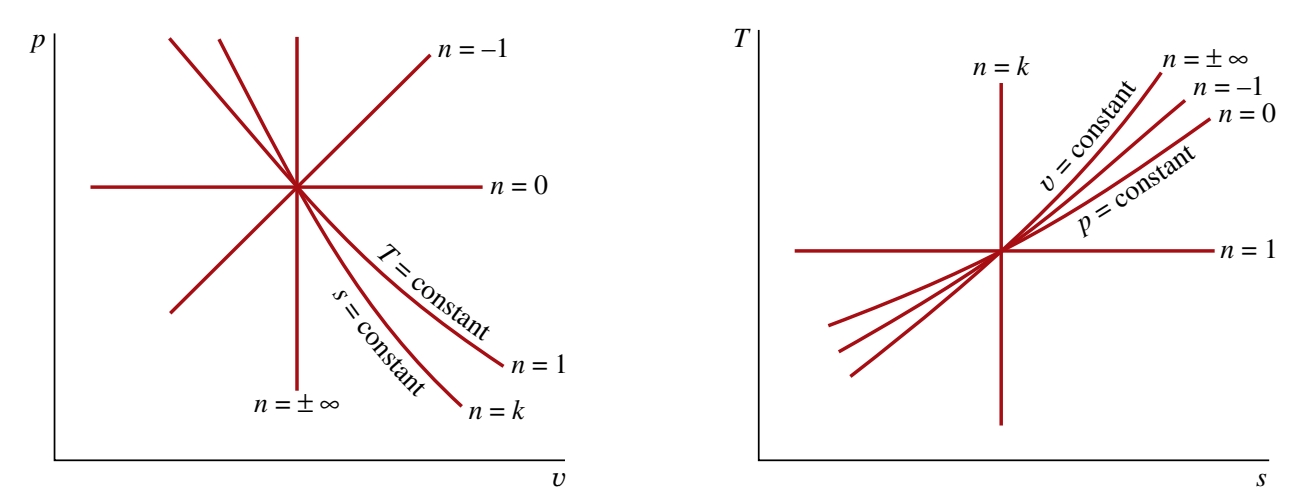
תהליכים פוליטרופיים על דיאגרמות ו- .

קצב שינוי אנטרופיה בנפח בקרה

קצב שינוי אנטרופיה בנפח בקרה בתהליך כללי

כמו מסה ואנרגיה, האנטרופיה היא תכונה אקסטנסיבית. לכן, גם היא יכולה לעבור לתוך ומנפח בקרה דרך זרימת מסה. כיוון שזהו השוני היחיד בין מערכת סגורה ונפח בקרה, נוכל לרשום את מאזן קצב שינוי האנטרופיה בנפח בקרה בצורה הבאה:

כאשר מתאר את קצב השינוי של האנטרופיה בנפח בקרה. הביטויים ו- הם השינויים באנטרופיה המלווים את זרם המסה לתוך והחוצה מהנפח בקרה, בהתאמה. הביטוי מאתר את קצב השינוי של אינטראקציית החום על הגבול בו הטמפרטורה היא . היחס מתאר את מעבר האנטרופיה על הגבול. הביטוי מתאר את קצב השינוי של היווצרות האנטרופיה כתוצאה מתהליכים בלתי הפיכים בתוך הנפח בקרה.

כפי שראינו בפרקים קודמים, לפי שימור מסה בנפח בקרה מתקיים:

לפי חוק ראשון עבור נפח בקרה:

לבסוף, נוכל לרשום את הביטוי למאזן קצב שינוי אנטרופיה בתהליך מתמיד:

אם יש כניסה ויציאה אחת:

הערה:

נזכיר כי לפי מוסכמות הסימונים, הוא החום שנכנס אל המערכת.

דוגמה:

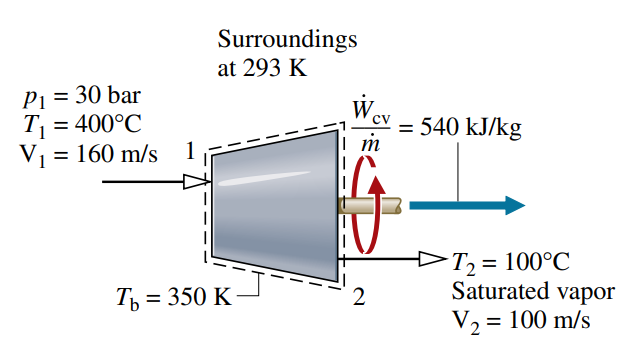
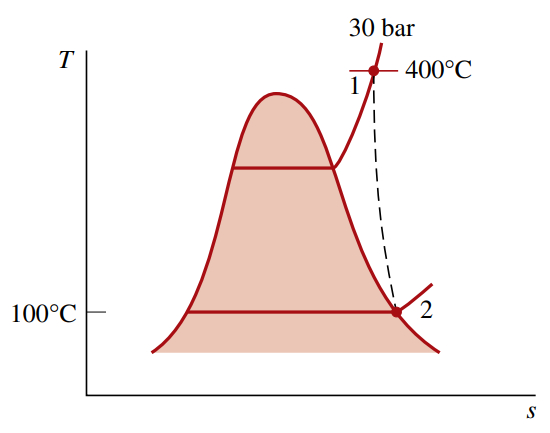
קיטור נכנס לטורבינה בלחץ , טמפרטורה ומהירות . אד שחון ב- יוצא במהירות . בתהליך מתמיד, הטורבינה מייצרת עבודה בגודל ל- של קיטור היוצא ממנו. אינטראקציית חום בין הטורבינה לסביבתה מתרחשת בגבולותיה בטמפרטורה ממוצעת של .
מצאו את הקצב בו אנטרופיה מיוצרת בתוך הטורבינה עבור של קיטור. הזניחו את השינוי באנרגיה פוטנציאלית בין הכניסה והיציאה.
פתרון:

ראינו כבר כי בתהליך מתמיד:

מאחר ואינטראקציית חום מתבצעת אך ורק ב-, ומתקיים שימור מסה כך ש- :

אנו יודעים כי בטורבינה לפי חוק ראשון:

נוכל למצוא את האנתלפיות והאנטרופיות מטבלאות קיטור. לאחר חישוב:

ולכן:

---

תרגיל:
מיכל מבודד שנפחו מחולק לשני חלקים שווים על ידי המחיצה. בתא השמאלי אוויר במצב ו-. בתא הימני ואקום.

1. חשבו את שינוי האנטרופיה אם המחיצה נשברת והאוויר מתפשט בבת אחת.
   פתרון:
   לפי חוק ראשון:

   מאחר וזהו תהליך אדיאבטי, וההתפשטות היא מול ואקום, הביטוי הימני מתאפס:

   נציב קיבולי חום כדי להסיק כי:

   לפי שינוי אנטרופיה של גז אידיאלי:

   נכפיל במסה כדי לקבל:

2. חשבו את העבודה שתפיק טורבינה אדיאבטית והפיכה שהאוויר מתפשט דרכה לצד השני של המחיצה. המחיצה מבודדת וקשיחה בתהליך.
   

   פתרון:
   מאחר והתהליך הוא אדיאבטי והפיך, נסיק כי זהו גם תהליך איזנטרופי. נסמן את המיכל עם האוויר ב- ואת המיכל עם הואקום ב-:

   נרשום את משוואת מצב עבור שני המיכלים:

   מאחר ואנו יודעים שכל התכונות שוות חוץ מהמסה, נסיק כי גם המסה שווה:

   לכן המסה בכל מיכל היא חצי מהמסה הכוללת:

   נשים לב כי זהו גם תהליך פוליטרופי, ולכן:

   חוק ראשון על כל המערכת ייתן:

   בנוסף, עבודת הטורבינה שווה לעבודת המערכת כי היא היחידה שמבצעת עבודה במערכת:

יעילות איזנטרופית

נעסוק כעת ביעילות האיזנטרופית של טורבינות ומדחסים. ניתן בקלות גם להרחיב את הגדרת היעילות לנפחי בקרה אחרים כמו מחליפי חום ומצערות.

יעילות איזנטרופית עוסקת בהשוואה בין הביצוע האמיתי של מכשיר כלשהו לביצוע שהיה ניתן להגיע אילו הוא היה מבצע את עבודה בצורה אידיאלית.

יעילות איזנטרופית של טורבינה

כדי להציג את הרעיון של יעילות איזנטרופית בטורבינה, נביט בדיאגרמת הבאה, המציגה את ההבדלים באנתלפיות בין טורבינה יעילה () לטורבינה לא יעילה :

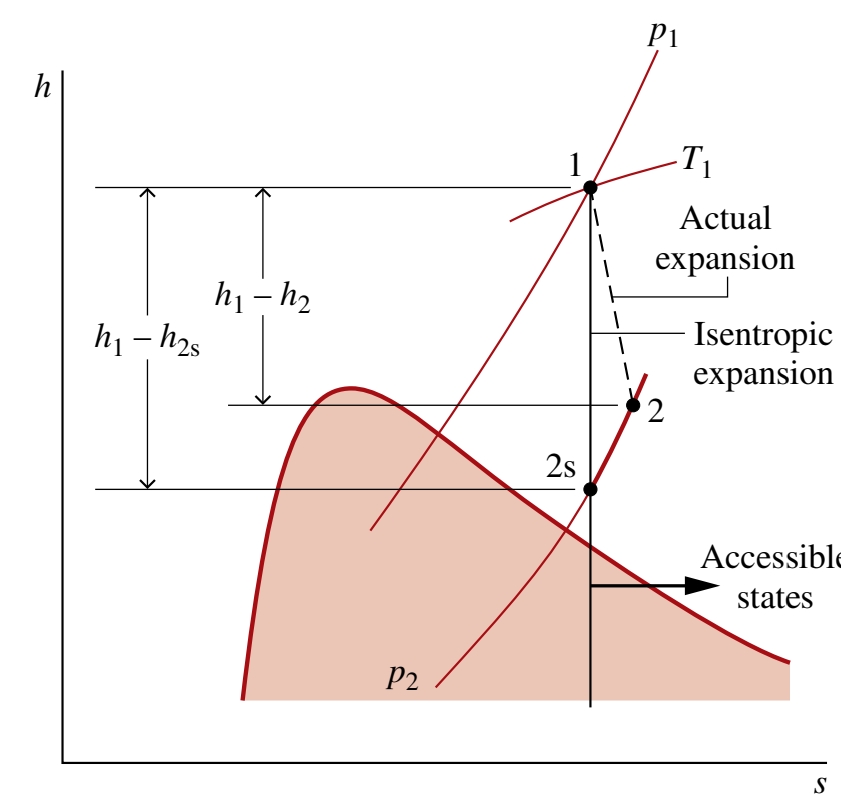
מצב המסה שנכנסת ויוצאת היא קבועה. אנו מניחים את אותם הנחות שקבענו בטורבינה בתהליך מתמיד. בנוסף, נניח כי אינטראקציית החום בין הטורבינה וסביבתה זניחה. לכן לפי חוק ראשון בתהליך מתמיד:

כאשר .
נניח כי מצב קבוע. ככל ש- קטן, העבודה שלנו תגדל. נקבל את העבודה המקסימלית כאשר האנתלפיה של המסה ביציאה היא מינימלית.

מאחר ואין מעבר חום, ישנו אילוץ על המצבים הסופיים, לפי קצב שינוי אנטרופיה בנפח בקרה בתהליך מתמיד:

הסיבה לכך היא שלפי חוק שני, לא יכל להיות שלילי. נסיק כי לא נוכל להגיע למצב כך ש- בתהליך התפשטות אדיאבטי. כלומר, חייב להתקיים:

המצב המתואר ב- בדיאגרמה הוא המצב שאליו מגיעים אם אין תהליכים בלתי הפיכים - תהליך איזנטרופי בטורבינה. מאחר וזוהי האנתלפיה המינימלית שנוכל להגיע אליה, העבודה המקסימלית היא:

הערה:

הסימון מעיד על לערך שחושב עבור תהליך איזנטרופי.

הגדרה:

היחס בין העבודה האמיתית לעבודה המקסימלית בטוריבנה מוגדר כהיעילות האיזנטרופית של טורבינה, הנקרא גם דרגת טיב של טורבינה.

יעילות איזנטרופית של מדחס

נביט בדיאגרמת עבור תהליך דחיסה:

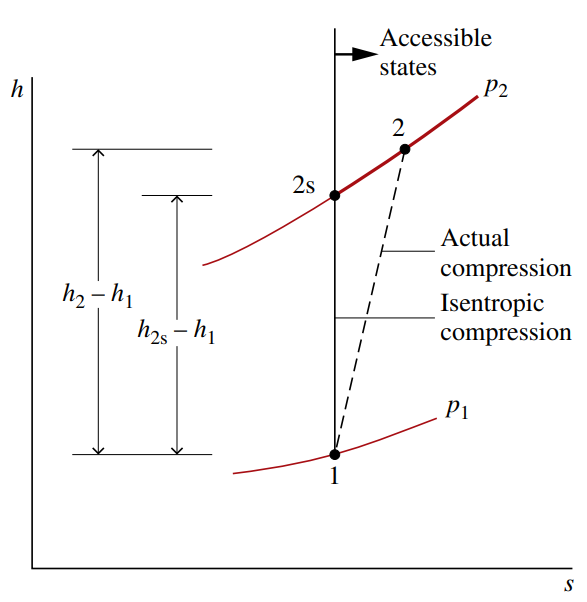
נזניח מעברי חום עם הסביבה ושינויים באנרגיה הפוטנציאלית והקינטית. לפי חוק ראשון בתהליך מתמיד:

נניח כי מצב קבוע. לכן, גודל העבודה תלוי באנתלפיה ביציאה, . ככל שה- יקטן, גם יקטן. נקבל עבודה מינימלית עבור האנתלפיה המינימלית שנוכל לקבל ביציאה. באותו אופן כמו בטורבינה, נקבל אנתלפיה מינימלית ביציאה עבור תהליך איזנטרופי:

בתהליך מציאותי, , כך שיותר עבודה מהמינימום תתבצע.

הגדרה:

היחס בין העבודה האמיתית לעבודה המינימלית במדחס מוגדר כהיעילות האיזנטרופית של מדחס, הנקרא גם דרגת טיב של מדחס.

---

תרגיל:

צילינדר אופקי ומבודד מחולק ל-2 חלקים בעלי נפחים שווים של ע”י בוכנה מבודדת המסוגלת לנוע ללא חיכוך. בהתחלה הנפח מכיל אוויר במצב זהה לזה של הסביבה ( ולחץ אטמוספרי) ונפח מכיל קיטור. כל המערכת נמצאת בשיווי משקל (מצב ). ברגע מסוים מתחיל לפעול מדחס אוויר אשר דוחס אוויר מהסביבה לנפח . במקביל מתחיל לזרום זרם חשמלי דרך נגד המספק הספק לנפח . במשך כל התהליך הזה הבוכנה לא זזה. בסוף התהלךי מופסקות זירמת האוויר דרך המדחס ופעולת הנגד והמערכת באה לשיווי משקל (מצב ), בו לחץ הקיטור והמדחס ביצע עבוד של .

1. מצא את הלחץ והטמפרטורה של האוויר במצב .
2. מצא את טמפרטורת הקיטור במצב והאינטראקציה עם הנגד.
3. האם האוויר עובר תהליך הפיך.
4. מה העבודה המנימלית של המדחס המאפשרת דחיסת האוויר עד ללחץ במצב .

פתרון:

1. במצב ההתחלתי שלנו, לפי הנתונים: בנוסף, הגענו לשיווי משקל בסוף, ולכן: נבחר כמערכת את האוויר במדחס ובגוף . נסמן אותה ב-. נוכל לחשב את המסה ההתחלתית: נרשום חוק ראשון בתהליך לא תמידי: אם נבצע אינטגרציה: כי אנו בתהליך אדיאבטי. בנוסף, כי אנו מזניחים את האנרגיה קינטית והאנרגיה הפוטנציאלית.
   נשים לב כי: כי המדחס בתהליך תמידי. לכן, מאחר ואנו במערכת פשוטה: ערך נתון לנו (המדחס צורך עבודה, ולכן זה יהיה במינוס), ואת אנו יכולים לפרק: לאחר הצבה: ולכן השינוי במסה: נותר לחשב את , שנוכל למצוא ממשוואת מצב:
2. נרשום את את הנתונים: אנו יודעים שהנפח לא השתנה, ולכן גם הנפח הסגולי לא השתנה: מטבלאות קיטור, נוכל למצוא כי אנו במצב רוויה כאשר: לכן: במצב יש לנו גם לחץ וגם . שוב מטבלאות קיטור: נבחר כמערכת את הקיטור כאשר הנגד עצמו מחוץ למערכת, ואז במקום עבודה שנכנסת למערכת, זה פשוט הופך לאינטראקציית חום. לפי חוק ראשון:
3. נחשב שינוי אנטרופיה, כאשר נסמן את טמפרטורות הסביבה ב-. לפי שינוי אנטרופיה של גז אידיאלי: נוכל להציב: ולכן התהליך לא הפיך.
4. עבודה מינימלית של המדחס תהיה כאשר המדחס איזנטרופי (אידיאלי) והתהליך בתא יהיה קוואזיסטטי. נשתמש במשוואות האיזנטרופיות על מנת לחשב את : ממשוואות מצב: ולכן השינוי במסה יהיה: חוק ראשון על תא והמדחס (בדומה לסעיף א’):

→ קודם: THE1_005הבא: THE1_007 ←