DEQ1_001 מבוא

→ קודם: DEQ1_000הבא: DEQ1_002 ←

מבוא

משוואה דיפרנציאלית

הגדרה:

משוואה דיפרנציאלית היא משוואה המקשרת בין משתנה בלתי תלוי לבין פונקציה לא ידועה ונגזרותיה .

משוואה דיפרנציאלית רגילה

הגדרה:

משוואה דיפרנציאלית רגילה (מד”ר) היא משוואה הנתונה ע”י:

סדר המשוואה - הסדר של הנגזרת הגבוהה ביותר המופיעה במשוואה, מסומן ב-.

דוגמאות:

למשל:

היא מד”ר מסדר 5.

הערות:

1. הסוג אחר של משוואה דיפרנציאלית היא משוואה דיפרנציאלית חלקית, ובה ישנם יותר משתנים בלתי תלויים ().

פתרון משוואה דיפרנציאלית

פתרון משוואה דיפרנציאלית היא כל פונקציה שמקיימת את המשוואה בקטע פתוח מסוים. כלומר, הוא פתרון של:

אם גזיר פעמים ומקיים את המשוואה בקטע כלשהו.
ניקח למשל את המד”ר:

נשים לב כי הפונקציה הבאה היא פתרון שלו בקטעים הפתוחים :

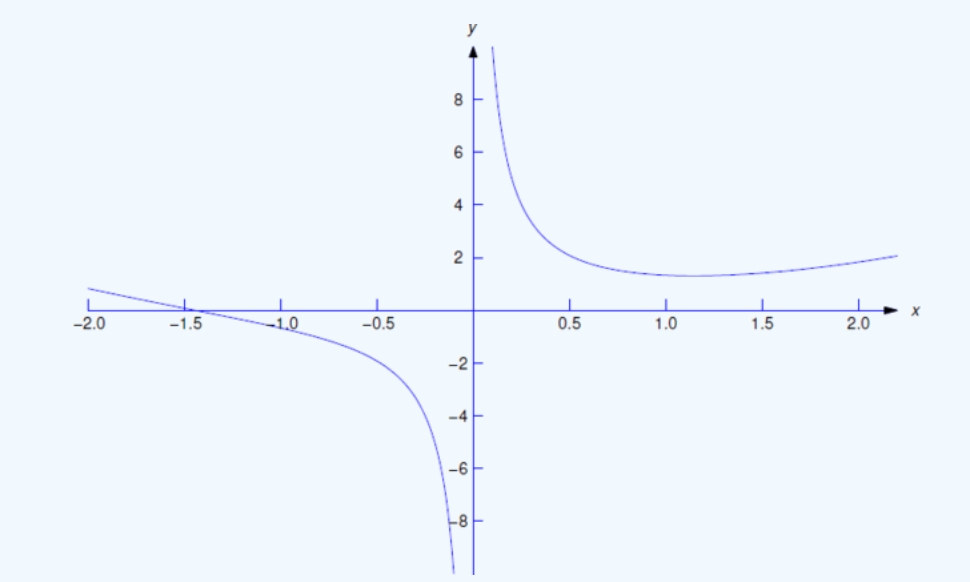
לגרף פתרון של משוואה דיפרנציאלית נקרא עקומת פתרון - וברוב המקרים ישנם אינסוף פתרונות כאלו, הפתרון הכללי:

כדי לקבל פתרון יחיד עבור משוואה דיפרנציאלית, לרוב נתונים גם תנאי התחלה - נקודה אחת על הגרף שמאפשרת לנו לצמצם את אינסוף האפשרויות לפתרון יחיד, ע”י הצבה פשוטה בפתרון הכללי.

הצגה גרפית של פתרון מד”ר

ישנם משוואות דיפרנציאליות שאי אפשר למצוא להן פתרון שניתן להציג בפשטות ע”י משוואות מתמטיות. במקרים כאלו ניתן להיעזר בהצגות גרפיות של הפתרון.

ניקח משוואה דיפרנציאלית מסדר ראשון, כלומר שהגזרת הכי גבוהה שם היא . משוואה כזו היא מהצורה:

אם ניקח קבוצה של נקודות, ונציב אותן ב-(1), נקבל את ערך בנקודה זו. במילים אחרות, את שיפוע הפונקציה בנקודה.

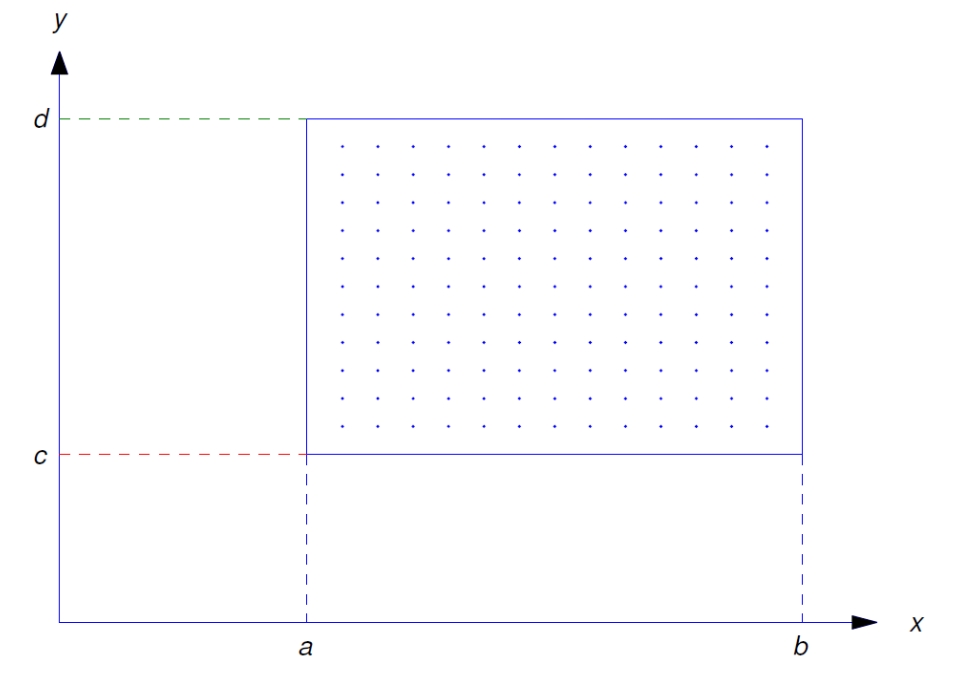
נשרטט את שיפועי המשיקים בנקודות כוקטורים עם כיוון המשיק, כלומר, , ונקבל את שדה כיוונים:

• עבור :
  

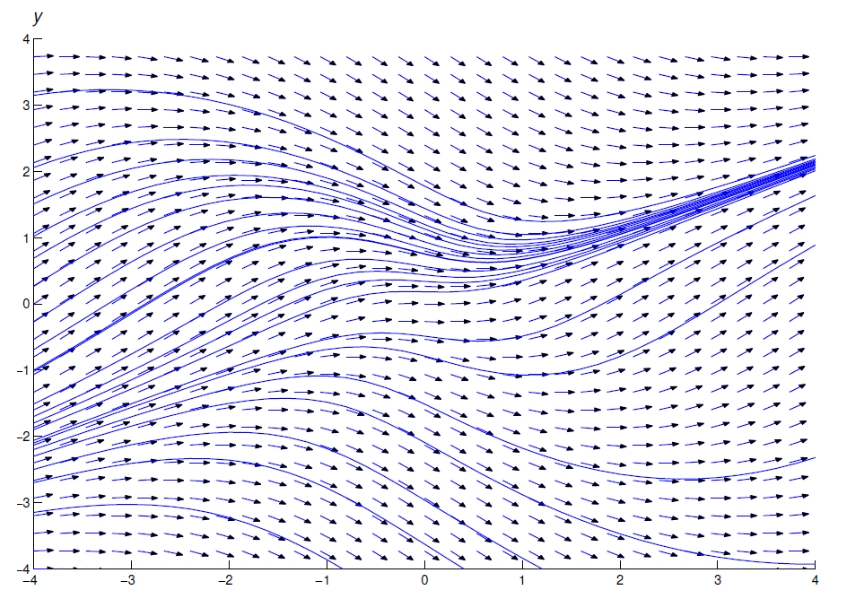
הערות:

1. ראש החץ מעיד על כיוון התקדמות השיפוע עם התקדמות הערך בכיוון החיובי.

סיווג מד”ר

מד”ר לינארית

הגדרה:

נאמר כי המד”ר לינארית אם המשתנים במשוואה לינאריים.

דוגמאות:

מד”ר הומוגנית

הגדרה:

עבור מד”ר כללית נאמר כי היא הומוגנית אם .

מד”ר מנורמלת

הגדרה:

עבור מד”ר כללית , נאמר כי היא מנורמלת אם . במצב זה נוכל לרשום:

→ קודם: DEQ1_000הבא: DEQ1_002 ←