ICT1_002 מודלים מתמטיים של מערכות

→ קודם: ICT1_001הבא: ICT1_003 ←

מבוא

כדי להבין מערכות בקרה מסובכות, עלינו לתאר אותם בעזרת מודלים מתמטיים. מאחר ורוב המערכות הן דינמיות בטבען, המודלים המתמטיים שיתארו אותם הם משוואות דיפרנציאליות. אם משוואות אלו ניתנות ללינאריזציה, אז נוכל להשתמש בהתמרת לפלס כדי לפשט את דרך פתרון הבעיה.
בתאכלס, הסיבוכיות של המערכות ואי הוודאות שלנו לגבי הפרמטרים הרלוונטיים כופה עלינו לבצע הנחות לגבי אופן פעולת המערכת.

משוואות דיפרנציאליות של מערכות פיזיקליות

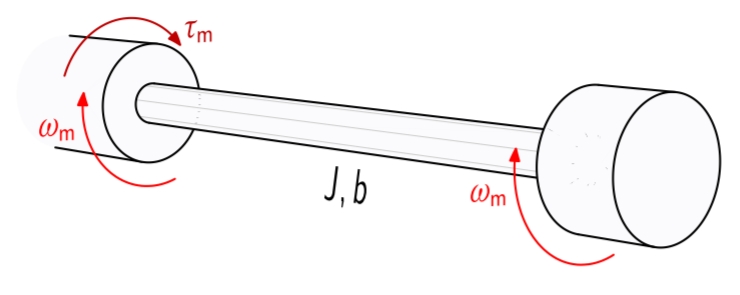
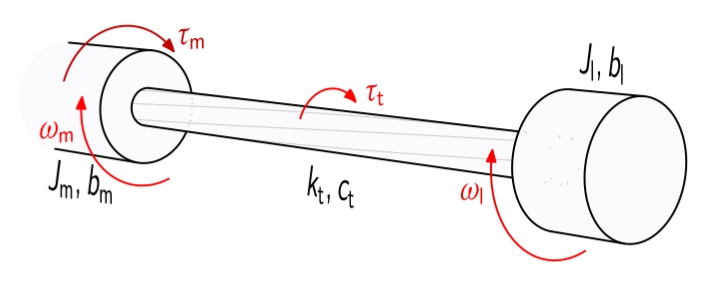
נתחיל מדוגמה של מערכת קפיץ-מסה פיתולית עם מומנט פיתול המופעל עליו:

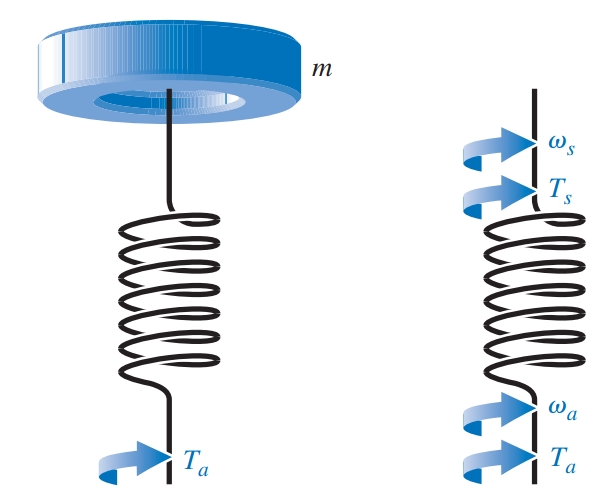
מערכת מסה-קפיץ פיתולית (torsional spring-mass system). (Dorf & Bishop, 2022).

נניח שהקפיץ חסר מסה ואנו רוצים למדוד את הפיתול המועבר למסה . מאחר והקפיץ חסר מסה, סכום המומנטי פיתול הפועלים על הקפיץ חייב להתאפס (שקול כוחות):

מה שאומר ש- . אנו רואים מיד שהמומנט פיתול החיצוני המופעל בסוף הקפיץ מועבר דרך הקפיץ פיתול. לכן, אנו קוראים לפיתול משתנה-דרך (through-variable). באותו אופן, הפרש המהירות הזוויתית הוא:

כלומר, הפרש המהירות הזוויתית נמדד לרוחב הקפיץ פיתול, ולכן אנו קוראים להפרש זה משתנה רוחבי (across-variable). באותו אופן אנו יכולים להכליל למקרים פיזיקליים שונים כדי לקבל את הטבלה הבאה:

סיכום של משתני דרך ומשתני רוחב עבור מערכות פיזיקליות. (Dorf & Bishop, 2022).

פונקציית תמסורת של מערכות לינאריות

הפונקציית התמסורת של מערכת ליניארית מוגדרת כהיחס של ההתמרת לפלס של הפלט להתמרת לפלס של הקלט, כאשר אנו מניחים תנאי התחלה אפסיים.
פונקציית התמסורת מוגדרת רק עבור מערכת לינארית וקבועה (קבועה בזמן). במערכת שהיא לא קבועה בזמן (time-varying system) לא נוכל להשתמש בהתמרת לפלס שלה. בנוסף, הפונקציית תמסורת היא תיאור של התנהגות הקלט-פלט של מערכת. כלומר, הפונקציית תמסורת לא מתארת את המבנה הפנימי של המערכת והתנהגותה.

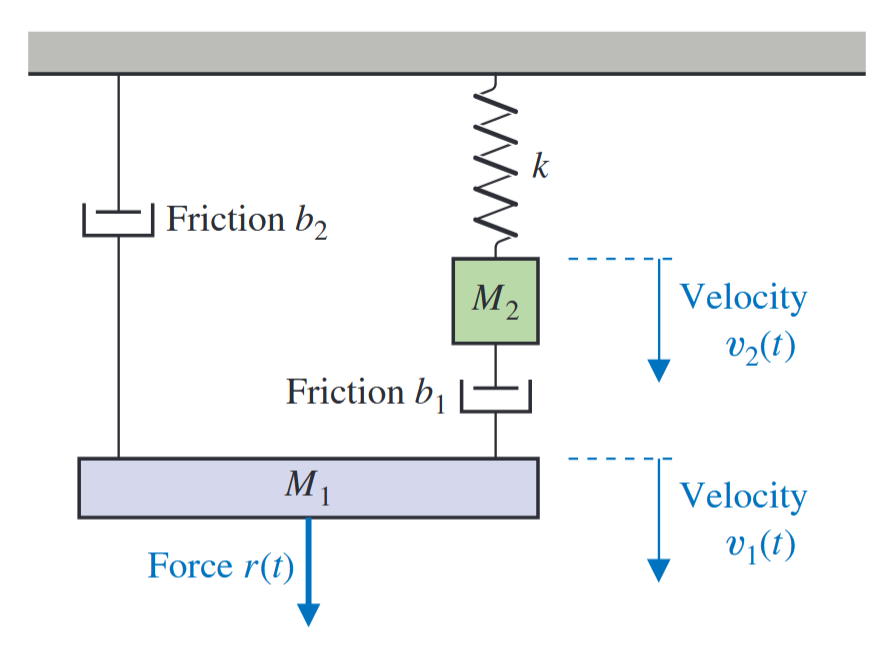
דוגמה: פונקציית התמסורת של מערכת שתי מסות

נביט במערכת המכנית הבאה:

מחוק שני על כל אחד מהמסות, לאחר התמרת לפלס, נקבל את המשוואה:

ועל המסה השנייה:

נסדר את שתי משוואות אלו כדי לקבל את מערכת המשוואות:

או, באופן מטריצי:

בהנחה והפלט שאנו מעוניים בו הוא המהירות של , אנו נפתור עבור :

כך הפונקציית התמרה של המערכת המכנית היא:

דיאגרמות בלוקים

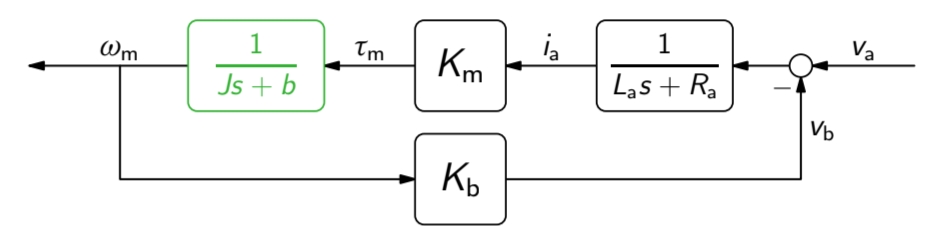
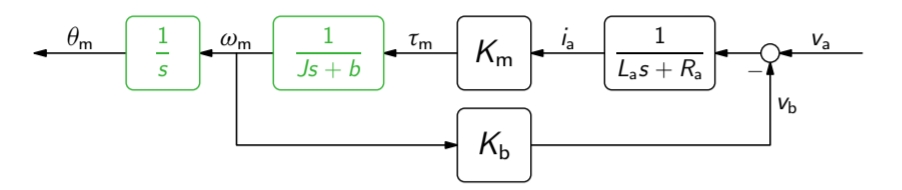
המערכות הדינמיות שמרכיבות מערכת בקרה משובית לרוב מתוארות מתמטית ע”י מספר משוואות דיפרנציאליות. ראינו במערכות לינאריות שאת המשוואות הדיפרנציאליות נוכל להפוך לפונקציית התמרה המקשרת בין הקלט והפלט של כל תת-מערכת. את קשר פעולה ותגובה זה נהוג להציג בדיאגרמת בלוקים. באיור הבא מוצג דיאגרמת בלוק של מנוע DC, שנראה איך מפתחים אותו בהמשך:

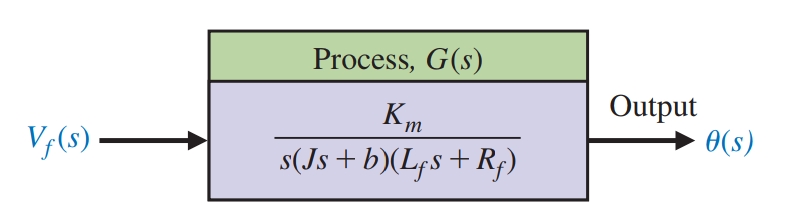
דיאגרמת בלוק של מנוע DC, עם מתח כקלט וזווית כפלט. (Dorf & Bishop, 2022).

כדי לתאר מערכת עם מספר משתנים בבקרה, נדרש להשתמש בחיבור בלוקים. למשל, המערכת באיור הבא כוללת שני משתני קלט ושני משתני פלט:

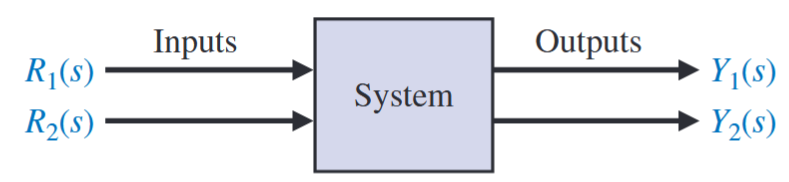
ייצוג בלוק של מערכת עם שני משתני קלט ושני משתני פלט. (Dorf & Bishop, 2022).

בעזרת הפונקציות התמרה נוכל לרשום את המשוואות המתארות את מערכת זו:

כאשר הוא הפונקציית התמרה שמקשר בין הפלט ה- לקלט ה-. הדיאגרמת בלוקים המייצגת את מערכת משוואות זו מוצגת באיור הבא:

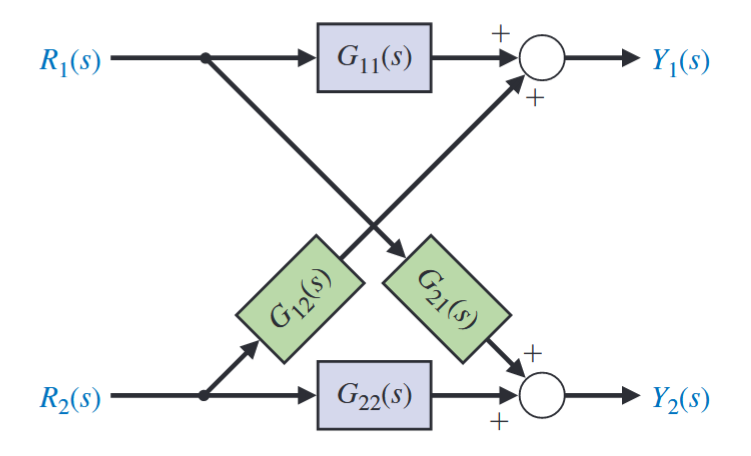
דיאגרמת בלוקים של מערכת עם שני משתני קלט ושני משתני פלט. (Dorf & Bishop, 2022).

במקרה הכללי, עבור קלטים ופלטים , נוכל לרשום את מערכת המשוואות באופן מטריצי:

או:

הדיאגרמת בלוקים של מערכת לרוב ניתנת לפישוט - הרי במערכות לינאריות פעולת ההכפלה היא קומוטטיבית. להלן טבלה המסכמת את אופן הפישוט:

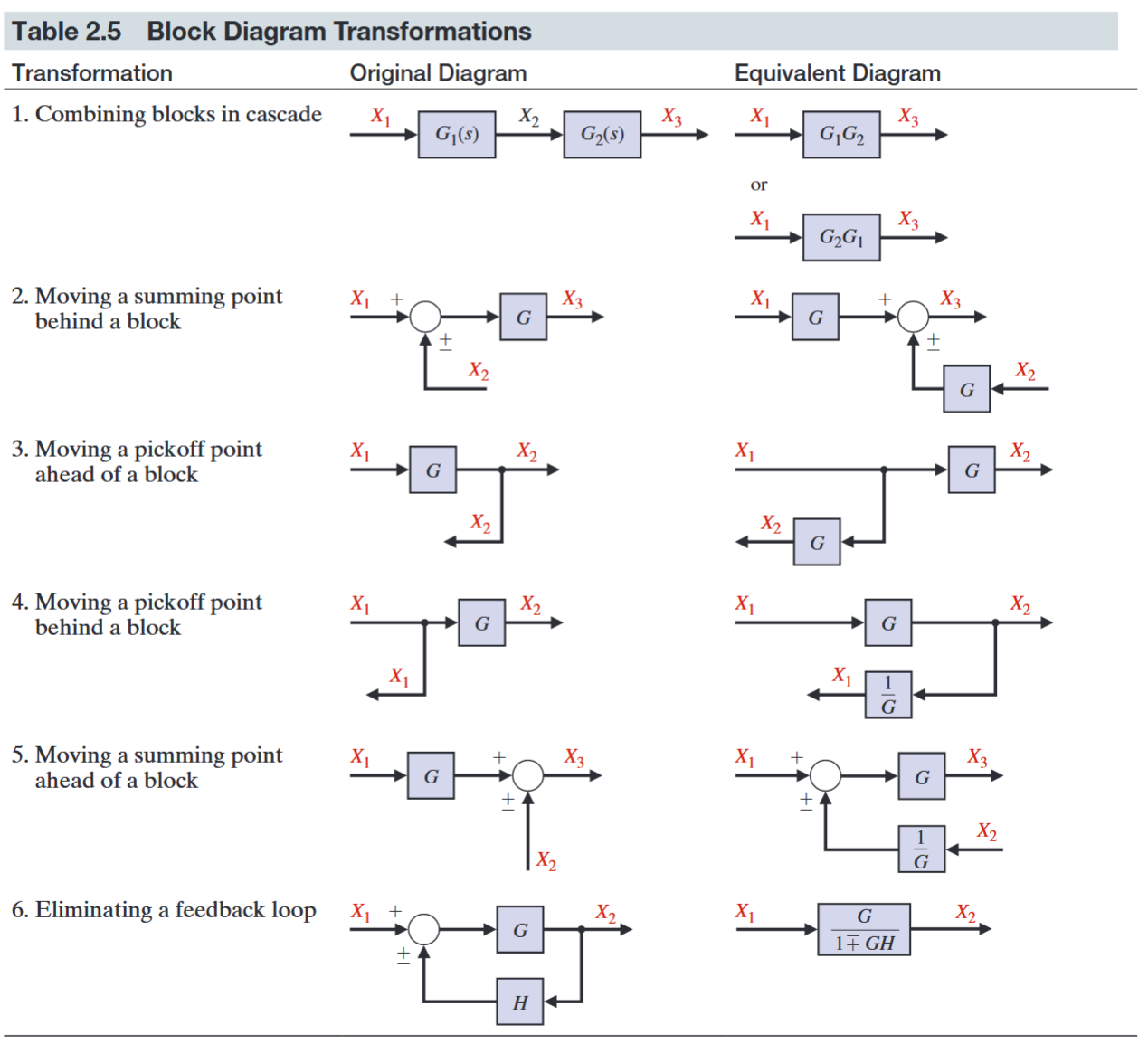
פישוט דיאגרמות בלוקים. (Dorf & Bishop, 2022).

דוגמה:

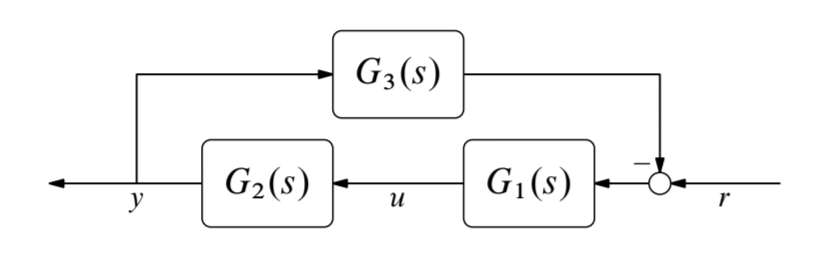
פשטו את הדיאגרמה הבאה ומצאו את הפונקציית תמסורת מ- ל-, ופונקציית תמסורת מ- ל-.

נוכל לרשום:

ולכן:

נסדר כדי לקבל ביטוי עבור :

ולכן:

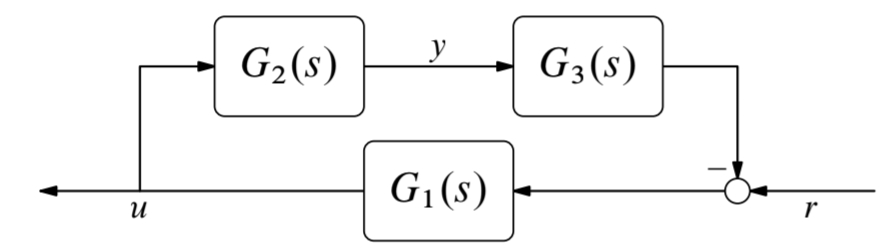
באותו אופן יכלנו להשתמש בחוק מספר 6 בטבלה לעיל כדי לקבל את תוצאה זו באופן מיידי. עבור נוכל גם להשתמש בחוק זה אם נסדר מחדש את הדיאגרמה:

ואז קל לראות ש:

מנוע DC

מנוע DC הוא מפעיל שמספק אנרגיה לעומס מסוים, כפי שמוצג באיור הבא:

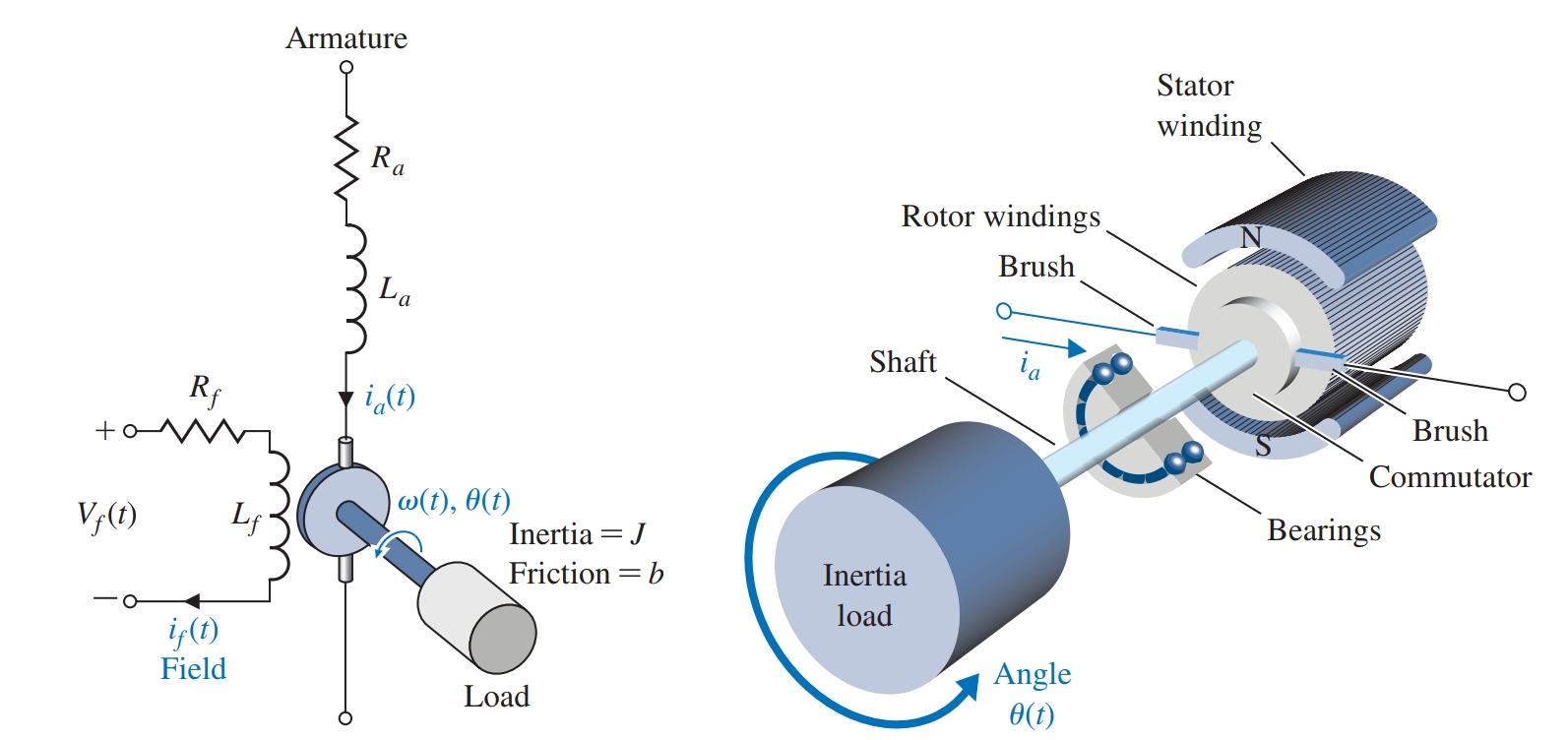
סכמה של מנוע ומעגל שקול שלו. (Dorf & Bishop, 2022).

המנוע DC ממיר אנרגיה חשמלית של זרם ישר (DC) לאנרגיה מכנית סיבובית. ישנם המון סוגים שונים של מנועי DC, ביניהם נלמד על מנוע brushed DC.
במנועים אלו המומנט הנוצר ע”י המנוע פרופורציונאלי לזרם בזרוע (צד ימין מופיע אותה המשוואה רק במישור לפלס):

כאשר נקרא קבוע המנוע (motor constant) או קבוע המומנט (torque constant).
הזרם בזרוע מקיים (לפי חוקי קירכהוף):

כאשר הוא המתח שהמנוע מקבל, בעוד הוא הכוח האלקטרומניע (כא”מ) החוזר - (back emf) הפרופורציוני למהירות סיבוב המנוע :

כאשר נקרא קבוע הכוח האלקטרומניע החוזר.

הערה:

בדרך כלל , תלוי ביחידות בהם משתמשים. בכללי:

בהתחשבות בהגדרות והמשוואות לעיל נוכל לבנות את הדיאגרמה הבאה:

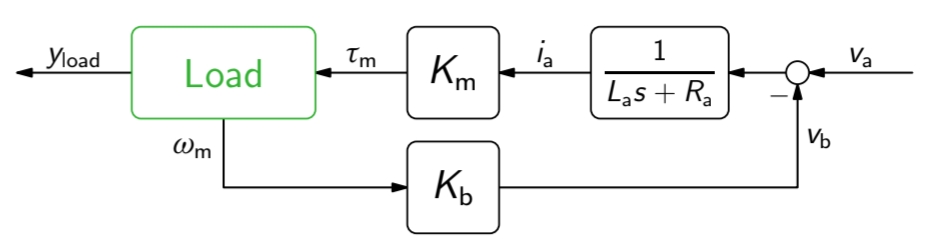
דיאגרמת בלוקים של מנוע DC כללי. הוא לא בהכרח (אבל יכול להיות המהירות הזוויתית של הגל . נראה את המקרים השונים בהמשך. (Leonid Mirkin’s Homepage, n.d.).

הערה:

נהוג (ורצוי) להפריד בין הבלוק ו- כי ביניהם אנו יכולים להוציא עוד ענף כדי לקרוא את הזרם , שלרוב נרצה לעקוב אחריו מסיבות שונות.

דוגמה: עומס מכני קשיח

בהנחה והעומס המכני קשיח לחלוטין (לא עובר דפורמציה), כאשר , משיווי משקל על הזרוע:

כאשר הוא מומנט האינרציה ו- הוא מקדם החיכוך.
במקרה זה:

מדיאגרמה זו ניתן לראות שהפונקציית תמסורת היא מהצורה:

שהוא תמיד יציב (מכנה פולינום ממעלה שנייה עם מקדמים חיוביים).
אם (הזווית של הגל), המערכת הופכת ל:

ולכן הפונקציית תמסורת:

שהוא לא יציב - יש לו קוטב בראשית.
בחלק מהמקרים, הקבוע זמן החשמלי קטן משמעותית מהקבוע הזמן המכני , כך שנוכל לפשט למערכת מסדר ראשון:

(כאשר מוזנח).

דוגמה: עומס מכני גמיש

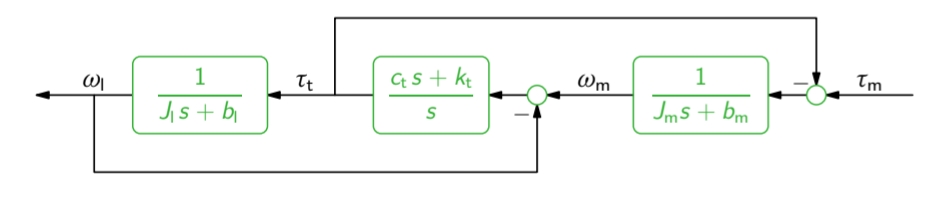
נביט כעת בעומס ( ו-) המחובר לגל ( ו-) ע”י תמסורת שהדינמיקה שלה מתוארת ע”י:

כאשר וגם , ו- ו- הוא המקדמי קשיחות והריסון, בהתאמה, של הריסון. המשוואות שנקבל משיווי משקל על כל חלק של התמסורת הם:

בדיאגרמת בלוקים:

תרגילים

תרגיל 1

האיור הבא מתאר מערכת לשליטה בזווית של אנטנה.

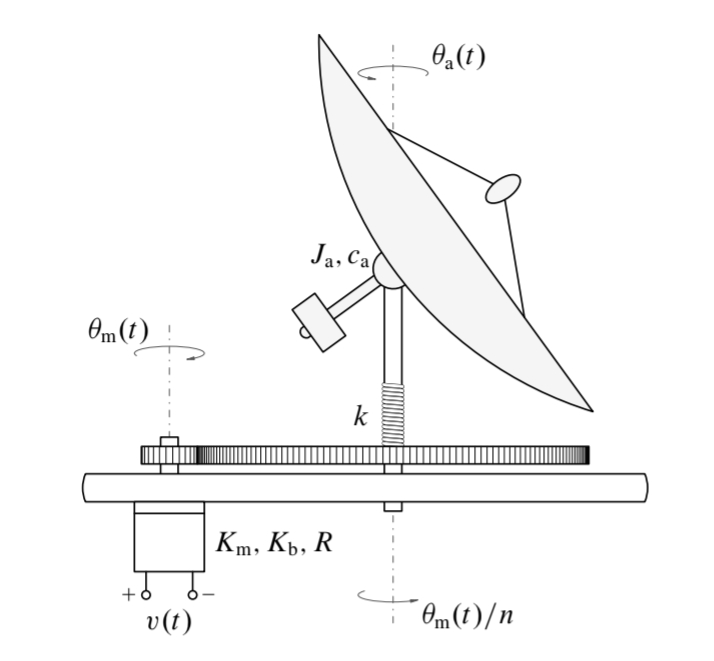
אנטנה מופעלת ע”י מנוע DC, עם תמסורת גג”ש וקפיץ. (Leonid Mirkin’s Homepage, n.d.).

האנטנה, בעלת מומנט אינרציה ושמאוזנת ביחס לציר האנכי, מסובבת ע”י המנוע DC עם קבוע מומנט , קבוע החזר כא”מ , התנגדות זרוע , עם אינרציה והשראת זרוע זניחה.
התמסורת כוללת שני גלגלי שיניים עם יחס , אינרציה זניחה, ומוט גמיש עם מקדם פיתול (קבוע קפיץ) וחיכוך (צמיגי) זניח - אין ריסון. בנוסף, למֵסַב מקדם חיכוך - יש ריסון. הקלט הוא המתח על המנוע DC.

סעיף א’

מצאו את משוואות התנועה של המערכת.

פתרון:
ללא הזנחת השראות, המשוואת מנוע DC:

נחלק ב-:

בהזנחת ההשראות נקבל:

מתח ההחזר emf הוא:

ולכן:

נכפול בקבוע מומנט :

הביטוי בצד שמאל הוא למעשה המומנט שהמנוע מפעיל:

במישור לפלס:

בעוד הוא קלט חיצוני, ה- הוא אות פנימי במערכת, שתלוי בדינמיקה של העומס כך שיש צימוד נוסף בין המנוע והעומס שלו.
נבנה משוואה ניוטונית עבור העומס (התמסורת והאנטנה). נשים לב שישנם שני מומנטים הפועלים על הגלגל שיניים הגדול - אחד מופעל ע”י הזרוע הגמישה, , ועוד אחד ע”י המנוע דרך המערכת גלגלי שיניים (שפשוט מגדיל אותו פי ). מאחר והמומנט אינרציה של הגלגל זניח, נקבל את השיווי משקל הבא:

על האנטנה מופעל המומנט ריאקציה מהקפיץ והמומנט מהחיכוך במסב, . נתייחס גם למומנט האינרציה של האנטנה:

המומנט שמופעל ע”י האנטנה הגמישה פרופורציונאלי למומנט של הקפיץ, כלומר להפרש בין הזווית של הגלגל שיניים וזווית האנטנה . הזווית של הגלגל שיניים תלויה בזווית המנוע ע”י היחס תמסורת, ולכן מומנט הזרוע:

המומנט שנוצר ע”י החיכוך במסב הוא:

נציב את כל המשוואות אחת בשנייה כדי לקבל את המשוואה הבאה עבור זווית זרוע המנוע:

או, במישור לפלס:

עוד משוואה שנקבל היא:

או, במישור לפלס:

סעיף ב’

בנו את הדיאגרמת-בלוקים של המערכת וחשבו את פונקציית התמסורת של המערכת .

פתרון:

דיאגרמת בלוקים של המערכת.

באופן שקול:

נוכל לקבל כעת ביטוי עבור לפי , ולאחר מכן ביטוי עבור לפי - מה שיניב לנו ביטוי עבור כנדרש.

→ קודם: ICT1_001הבא: ICT1_003 ←