טרנספורמציית לפלס
טרנספורמציית לפלס היא טרנספורמציה המאפשרת פתרון של מד”ר כללית עם מקדמים קבועים (גם לא הומוגנית) בתנאי שתנאי ההתחלה נתונים עבור
יתרונות פתרון בעזרת התמרת לפלס:
- הפתרון מתקבל בצורה מלאה ישירות - אין צורך להציב את ת”ה למציאת הקבועים.
- פותרים משוואה אלגברית ולא דיפרנציאלית.
הגדרה:
תהי
פונקציה המוגדרת עבור , ותהי . אזי הטרנספורמציית לפלס של היא הפונקציה : עבור ערכי
בהם האינטגרל המוכלל מתכנס.
את הטרנספורמציה נהוג לסמן:
דוגמה:
נמצא את ההתמרת לפלס ל-
: אם
, אז: ולכן:
מאחר ו-
לא מוגדר, ומצאנו ש: תוצאה זו ניתנת לכתיבה כ:
מאחר ואין לנו כוח לחשב אינטגרלים מוכללים שאף אחד לא זוכר איך לחשב, ניעזר בטבלה:
טבלת טרנספורמציית לפלס
לינאריות לפלס
משפט:
תהי
ו- . אזי: לכל קבוע
.
תרגילים:
- המד”ר:
נפעיל התמרת לפלס על המשוואה: - המד”ר:
- המד”ר:
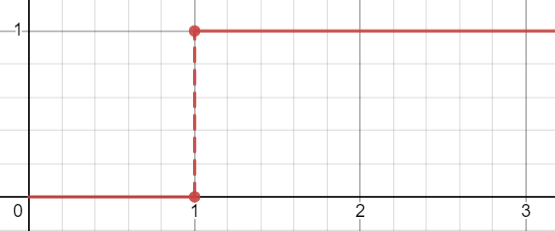
פונקציות מדרגה
הגדרה:
פונקציית מדרגה (Heaviside) היא פונקציה מהצורה הבאה:
הזזה של מדרגה:
תרגילים:
- המד”ר:
נסמן את אגף ימין ב-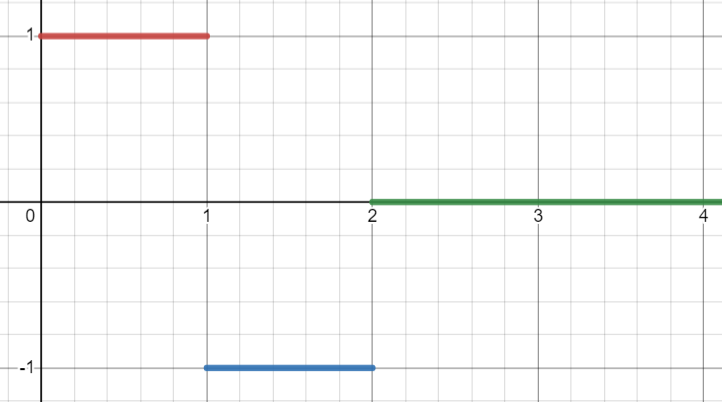
נקבל כי - המד”ר:
נרשום כפונקציית מדרגה: - המד”ר:
נשים לב כי:
נוסיף פתרון של החלק ההומוגני.
פ”א: