DVI1_004 ריסון וקשיחות לא לינארית

→ קודם: DVI1_003הבא: DVI1_005 ←

הטיפול בבעיות עם ריסון לא לינארית או קשיחות לא לינארית הוא טכני לחלוטין, ומספיק להבין מהתרגילים:

תרגילים

תרגיל 1

נתונה מערכת עם משוואת התנועה הבאה:

הערה:

היחידות של שאנו מכירים הם , בעוד של הם .

סעיף א’

בצעו נרמול של המשוואה.

פתרון:
נחלק במסה ונקבל:

נגדיר תדירות טבעית וזמן מנורמל:

נמצא נגזרות ע”פ זמן מנורמל:

נציב במשוואה:

כאשר סימנו . נסמן גם , ונקבל:

נסמן את המקדם של ב- ונקבל:

סעיף ב’

חשבו את ההספק היוצא מהמערכת כתוצאה מריסון לא לינארי, בזמן מחזור.

פתרון:
נפעל באופן דומה לשיטת האיזון האנרגטי.
נניח פתרון תונד כללי:

הביטוי לעבודה של כוח לא משמר לאורך מחזור הוא:

במקרה שלנו, נעביר את הריסון אגף, כך שאנו בעצם מסתכלים עליו ככוח:

ולכן נסמן, . לכן העבודה שלו בזמן מחזור אחד:

נחשב את :

ניזכר ש- , כך ש כאשר מציבים באינטגרל, גם לאחר האינטגרציה, כל הביטויים עם האקספוננטים מצטמצמים ומקבלים:

סעיף ג’

חשבו את ההספק היוצא מהמערכת כתוצאה ממרסן לינארי והשוו הספקים לקבלת .

פתרון:
עבור המקרה הלינארי, משוואת התנועה שלנו היא:

ולכן העבודה שלו:

נחשב את כמו מקודם ונקבל:

נשווה בין ההספקים:

סעיף ד’

בנו תגובת תדירות למשוואת המרסן השקול שהתקבל.

פתרון:
קיבלנו משוואה שקולה:

הערה:

נשים לב שהריסון השקול שקיבלנו הוא פונקציה של עוצמת (magnitude) הפתרון!

ננחש פתרון:

נציב במשוואה (כאשר נזכור ש- ):

נקבל ש:

קיבלנו משוואה סתומה. נעלה אותה בריבוע כי זה מה שרשום בדפים:

ניתן לחשב גם את הפאזה:

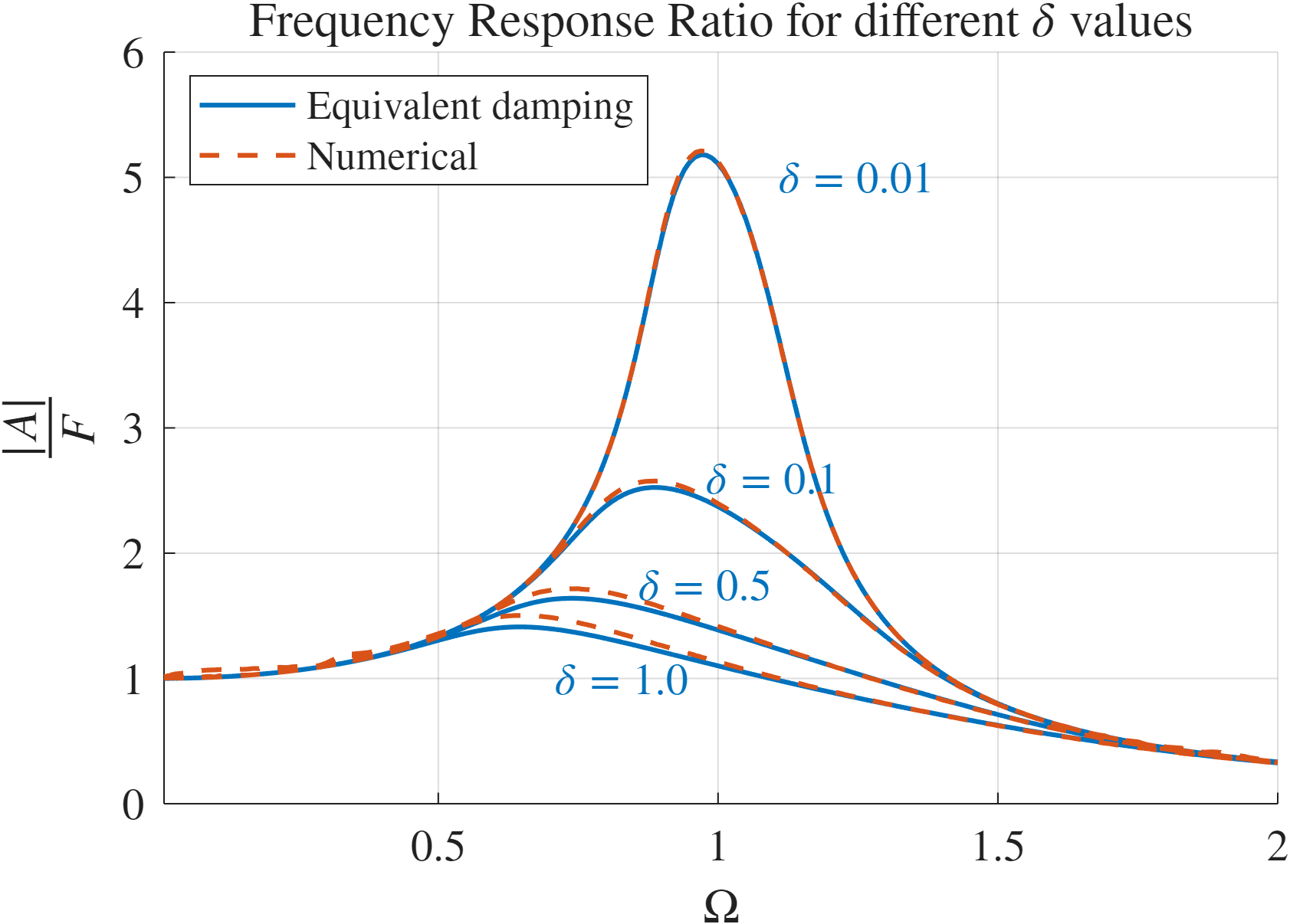
דיאגרמת עוצמה לפתרון נומרי וקירוב לפתרון. הגרפים השונים מייצגים ערכי ריסון שונים.

הציר האנכי בגרף מבטא את היחס .

• מתקבל דיוק מספק בין הפתרון הנומרי המשקלל ריסון לא לינארי לפתרון המקורב אשר מתבסס על ריסון שקול.
• צמצום הריסון גורם להגדלת השפעת התהודה (resonance) על היחס בין אמפליטודת התגובה לבין העומס.
• ריסון לא לינארי איננו משפיע על התדירות העצמית של המערכת, מה שמתבטא בתהודה סימטרית.

הקוד נמצא בGitHub.

תרגיל 2

נתונה המערכת הבאה:

סעיף א’

נתחו את התדר הטבעי של המערכת כתלות באמפליטודה.

פתרון:

הערה:

כשמוצאים תדר טבעי מתעלמים מעומסים שפועלים ומריסון.

נמצא את התדירות הטבעית:

נבצע נרמול של המשוואה:

נקבל כי:

נציב בחזרה במשוואה:

נסמן :

ננחש פתרון:

כדי להציב במשוואה נצטרך גם לחשב את :

נזניח תדירויות גבוהות (נתעלם מ- ), ונציב במשוואה:

קיבלנו קשר בין תדירות הפתרון לעוצמת (magnitude) הפתרון, מה שיבוא לידי ביטוי בגרף בסעיף הבא.

סעיף ב’

הציגו את תגובת המערכת לכניסה כתלות האמפליטודה.

פתרון:
נחזיר את הכוח והריסון:

נחלק ב-:

ננרמל את המשוואה:

נקבל ש:

ננחש פתרון:

נזניח תדירויות גבוהות ונציב במשוואה הדיפרנציאלית:

נקבל שכל כופל של אקספוננט מתאפס בנפרד ולכן נקבל שתי משוואות:

נמצא גודל בריבוע ונבודד:

והפאזה שמתקבלת:

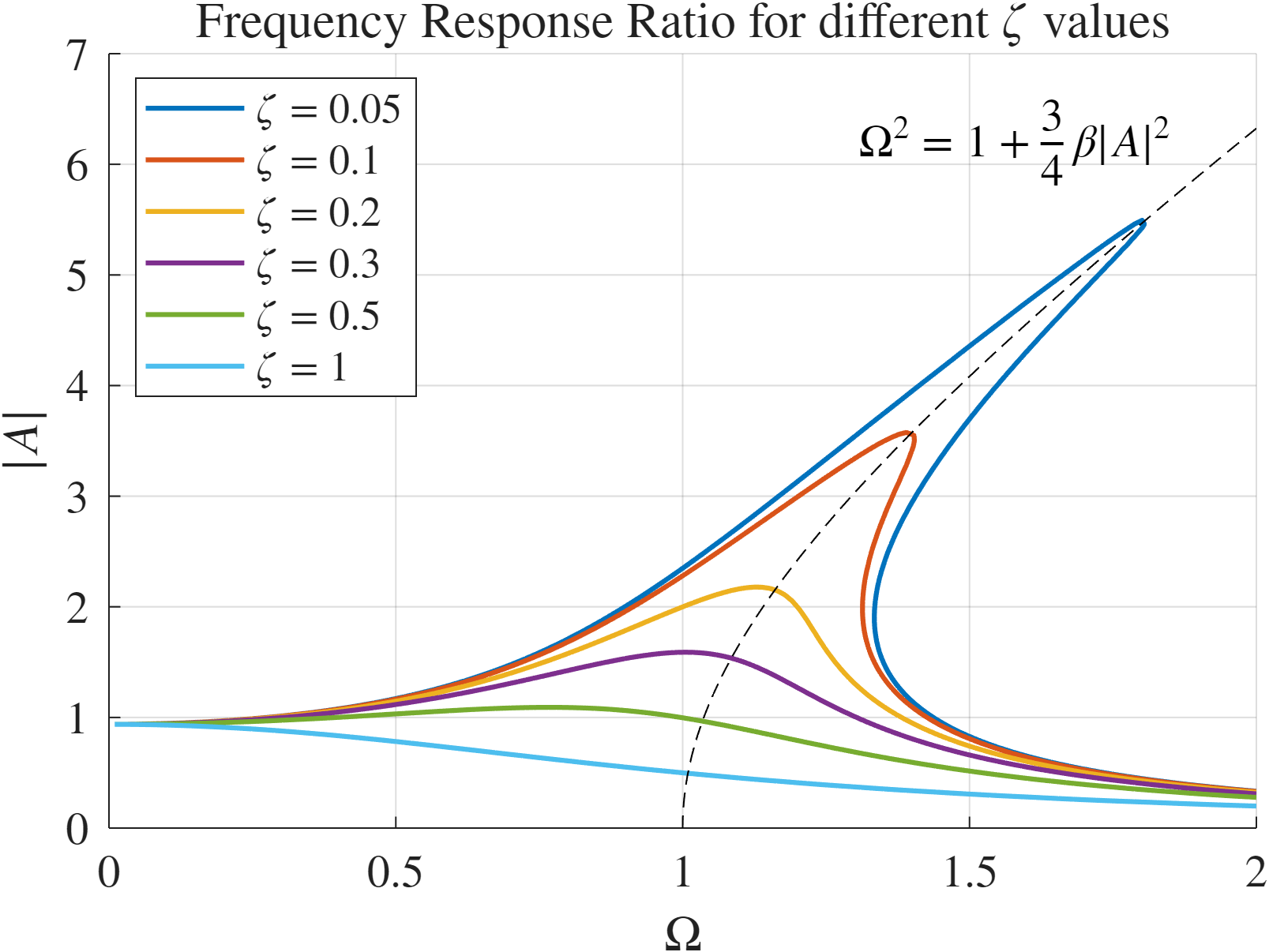
הקשר בין יחס בין אמפליטודת התגובה לבין העומס, ל-בין תדירות העומס.

נשים לב כי:

1. הגדלת הריסון מביאה לצמצום יחס האמפליטודה תגובה-עומס.
2. צמצום מנת הריסון גורמת להגדלת יחס האמפליטודה תגובה-עומס, מה שגורם להגדלת התדירות העצמית. תופעה זו מייצרת תהודה לא סימטרית.
3. נקודות הקיצון של עקומי הריסון השונים מרכיבות עקום של יחס אמפליטודת התגובה-עומס בתלות התדירות.

הקוד נמצא בGitHub.

→ קודם: DVI1_003הבא: DVI1_005 ←