DVI1_HW001 פרויקטון 1

	סטודנט א’	סטודנט ב’
שם	עידו פנג בנטוב	יובל הנדל
ת”ז	CLASSIFIED	CLASSIFIED
דואר אלקטרוני	CLASSIFIED	CLASSIFIED

הקוד נמצא בGitHub.

---

---

הערה:

ציון:

שאלה 1

ניתן לתאר את דינמיקת המערכת עם , כאשר את שאר המשתנים (למשל ) נוכל לתאר בעזרת . מבחינת דרגות החופש, יש לנו דרגת חופש אחת, , שבעזרתה ניתן לתאר את המערכת בכל זמן נתון.

שאלה 2

וקטור המיקום של המסה:

מאחר ותנועת המערכת מוגבלת לציר אחד, מעתה לא נרשום את הצירים בביטויים, כך שנעבוד רק עם סקלרים:

נבטא את האנרגיה הקינטית של המסה (החרוז הוא החלקיק היחיד עם מסה במערכת):

האנרגיה הפוטנציאלית, יחסית למצב בו :

כאשר שמנו לב שאורך הקפיץ בכל רגע נתון הוא .

שאלה 3

מבחינת קואורדינטות מוכללות, יש לנו רק את , וגם רק חלקיק אחד, .
העומסים הפועלים על החלקיק (שלא התחשבנו בהם בחישוב האנרגיה הפוטנציאלית) הם כוחות הריסון והמומנט. לכן הכוח המוכלל יהיה מהצורה הבאה:

נשים לב ש- , כך שנקבל:

שאלה 4

הלגראנז’יאן (לפי (2.1) ו-(2.2)):

נציב במשוואת לגראנז’ (ניעזר ב-(3.1)):

שאלה 5

הערה של הבודק:

עדיף לנתח יציבות לפי אנרגיה פוטנציאלית, מתי הנגזרת שלה חוצה את האפס, קמירות בנקודות וכו’.

עבור , משוואת התנועה (4.1) הופכת להיות:

נמצא את נקודות שיווי המשקל ע”י הצבת :

מהצבת הנתונים ב-python נקבל פתרון פיזיקלי יחיד (השאר מרוכבים):

נגדיר:

ולכן נקודת שיווי המשקל היא:

נוכל כעת לרשום את (5.1) בצורה מטריצית:

נסמן את הצד הימני של המשוואה ב-:

נגזור ונציב את הנקודת שיווי משקל:

נציב נתונים:

נמצא ערכים עצמיים של כדי לאפיין את נקודת שיווי המשקל :

כיוון שהחלק הממשי שלילי, נסיק כי נקודת שיווי המשקל יציבה. בנוסף, כיוון שיש חלק מדומה, נסיק כי הכינוס לנקודת שיווי המשקל תונד, כך שנוכל לאפיין את נקודה זו כ- (stable focus).

שאלה 6

נציב את אותם הנתונים רק עם ב-(5.2) ובאותו אופן נקבל שלוש נקודות שיווי משקל (לאחר הצבה ב-python):

נאפיין כל אחת מהן:

• עבור (לאחר הצבה ב-(5.3)): הערכים העצמיים שלה: ולכן היא .
• עבור : הערכים העצמיים שלה: ולכן היא נקודת אוכף - .
• עבור : הערכים העצמיים שלה: ולכן היא .

שאלה 7

המקרה האחר הוא כאשר יש שתי נקודות ש”מ, ונראה מתי הוא מתרחש, אם בכלל.
משוואה (5.2) קושרת בין ו-. ראינו שעבור ערכים מסוימים של אנו מקבלים פתרון יחיד ל- ועבור ערכים מסוימים מקבלים שלושה. נבודד את כדי למצוא האם יש ערך מסוים של עבורו יש שני פתרונות ל-:

נביט בגרף הנוצר (עבור הנתונים):

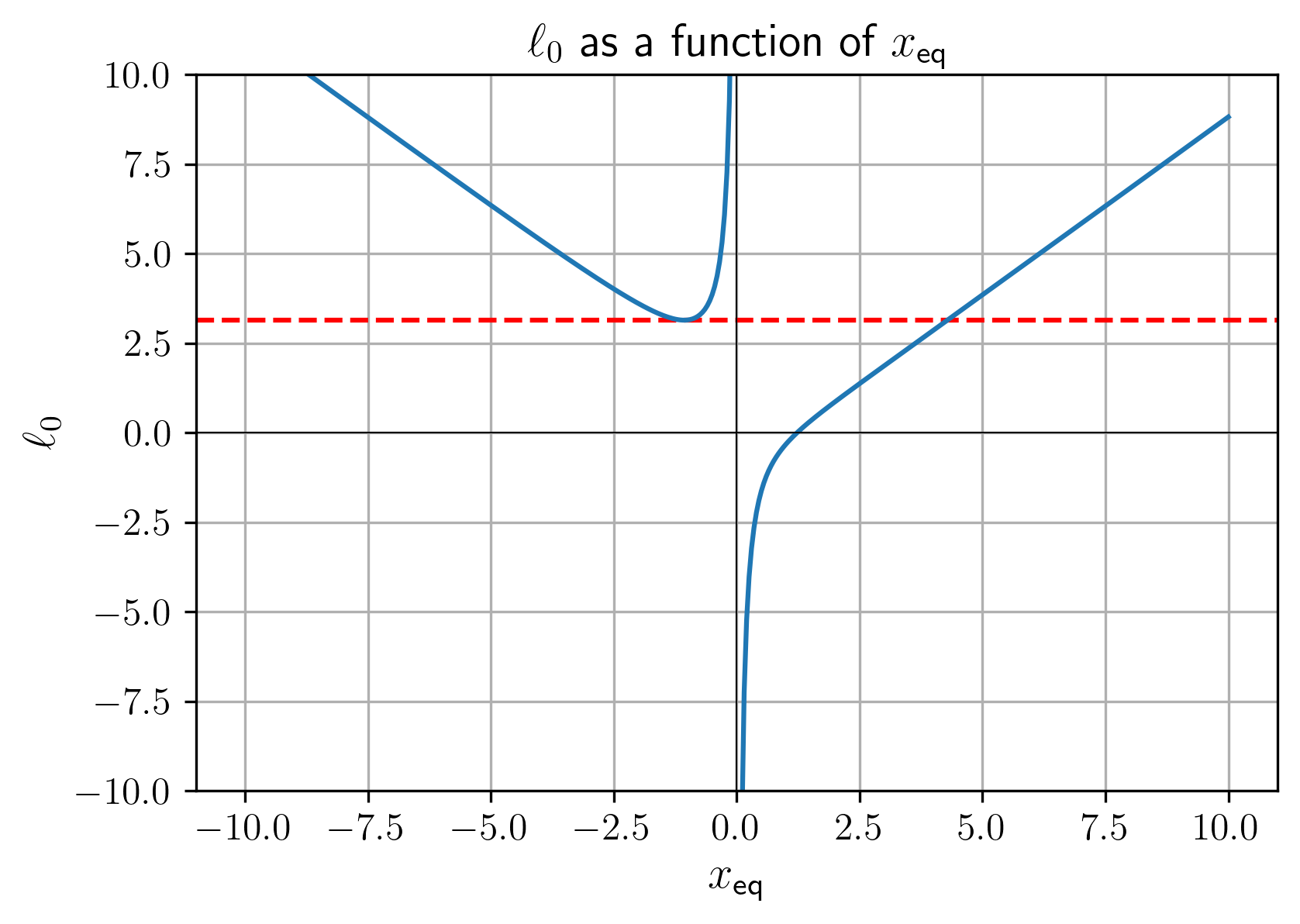
איור 1: הפונקציה כפי שנתון במשוואה (7.1).

נשים לב שישנו ערך יחיד של בו מתקבלים שני ערכים ל-. ערך זה מתקבל במינימום, אז נמצא אותו ע”י גזירה של לפי :

נשווה לאפס (כדי למצוא מינימום):

נציב נתונים ונקבל:

כמובן שזו לא נקודת שיווי המשקל היחידה, אבל בעזרתה נוכל למצוא את בעזרת הצבה בחזרה ב-(7.1):

אורך זה, שנקרא לו האורך הקריטי, הוא בדיוק האורך החופשי של הקפיץ בו נקבל שתי נקודות שיווי משקל.
נשרטט את האנרגיה הפוטנציאלית לפי עבור ערכי שונים:

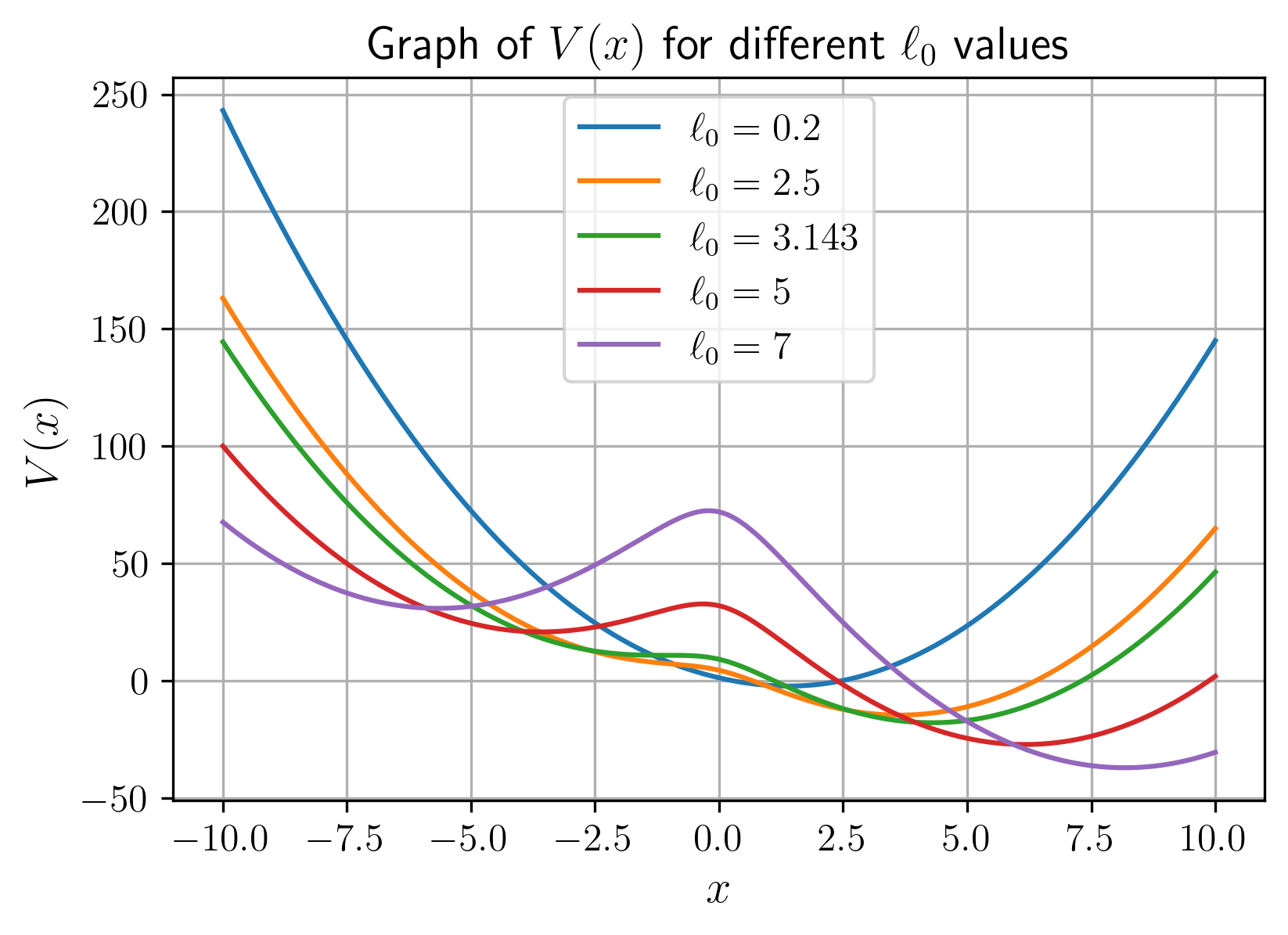
איור 2: פונקציית הפוטנציאל עבור ערכי שונים.

---

---

שאלה 8

נגדיר את משוואה (5.2) כפונקציה:

ונביט בקווי הגובה שלה ב- :

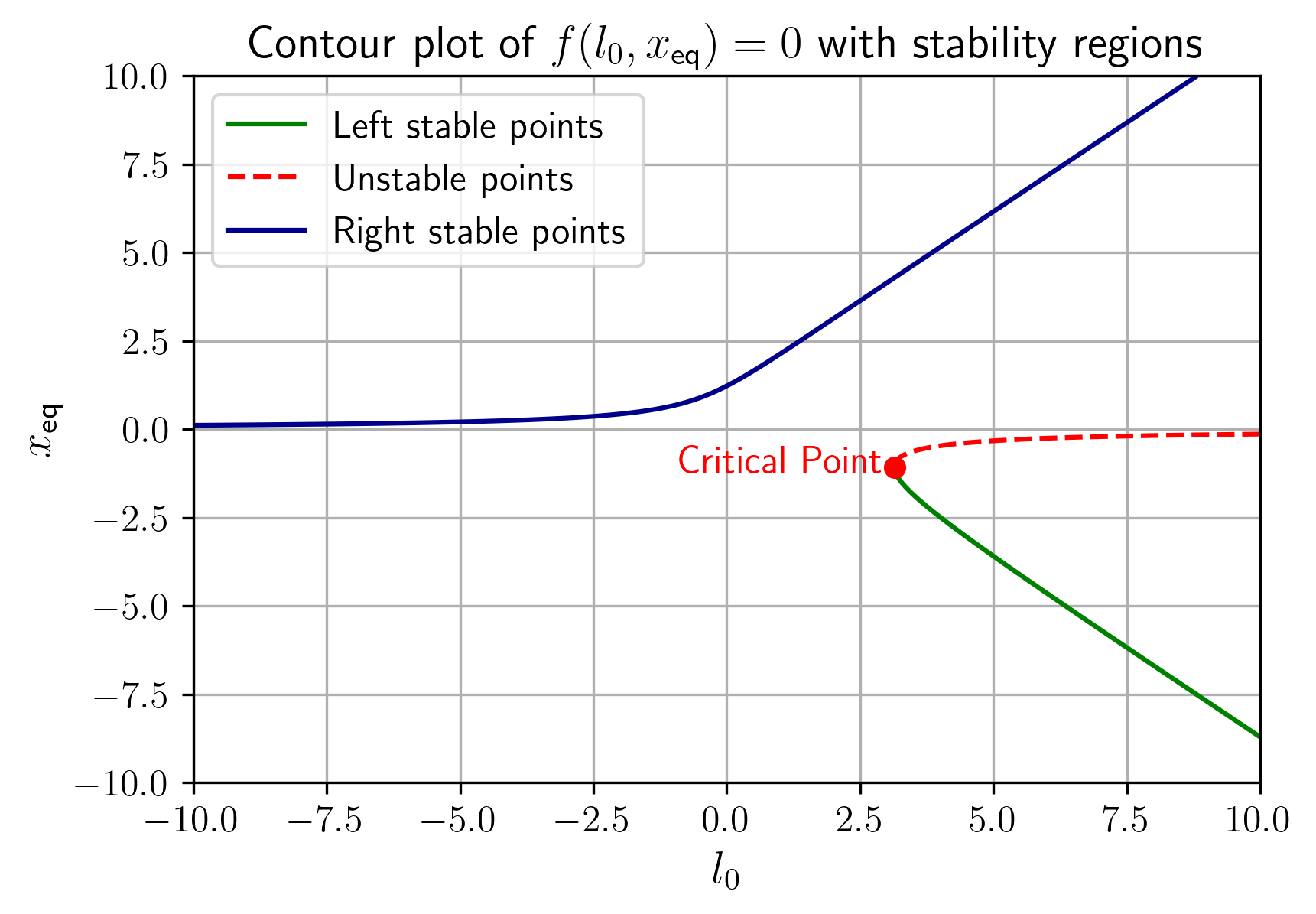
איור 3: סיווג יציבות במערכת לערכי שונים.

מהגרף הנ”ל והגרף הקודם אנו רואים שהנקודה הקריטית היא נקודה מעניינת שנאפיין אותה כ-semi-stable, שאם התנאי התחלה יהיה מימין אליה, היא תתבדר, ואם תנאי ההתחלה יהיה משמאל אליה, היא תתייצב בחזרה לנקודה.

שאלה 9

נחזור למשוואה (5.2), בצורה המטריצית:

נמדל את המערכת עבור תנאי התחלה שונים והערכים .

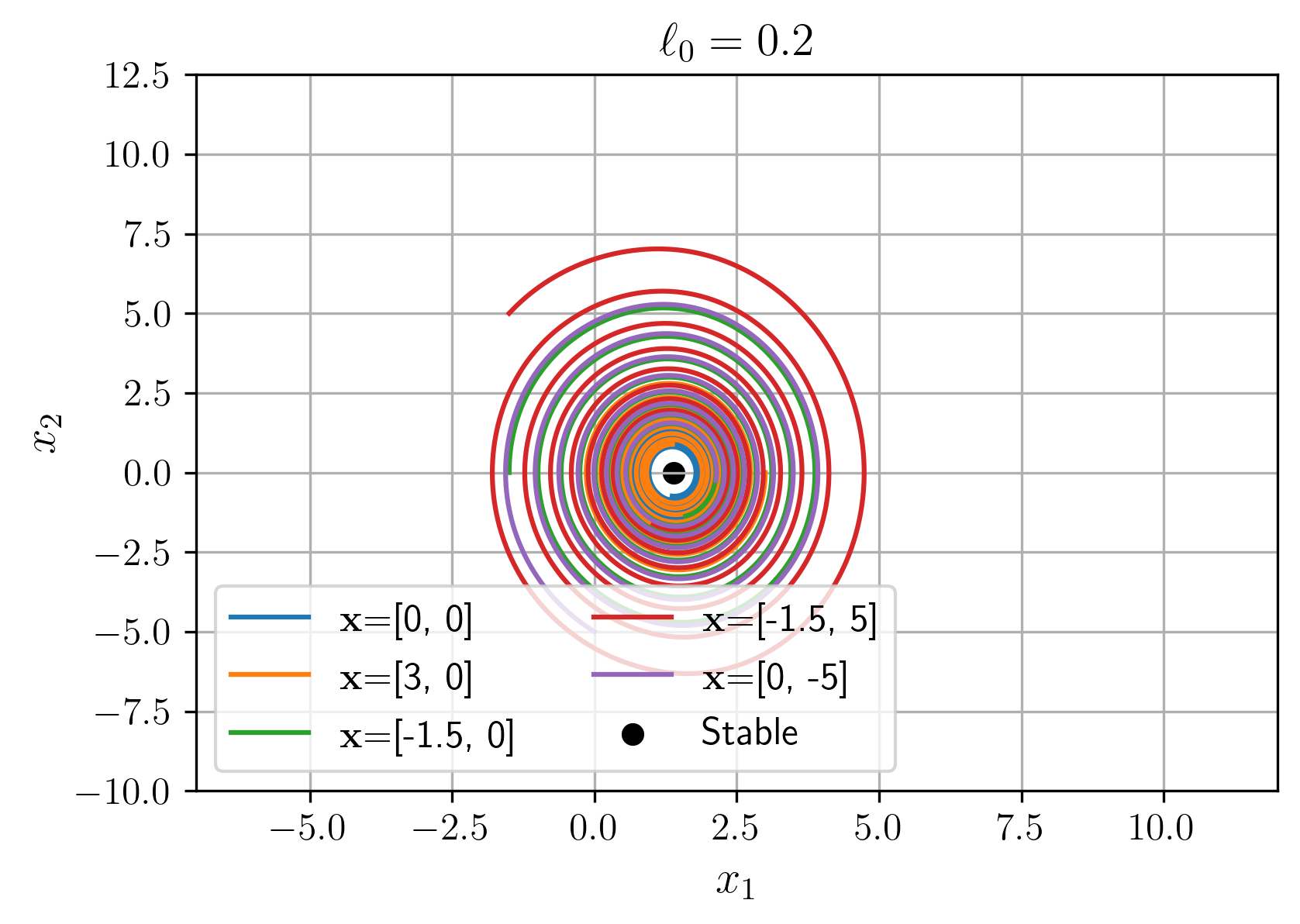
איור 4: מרחב המצב של המערכת עבור .

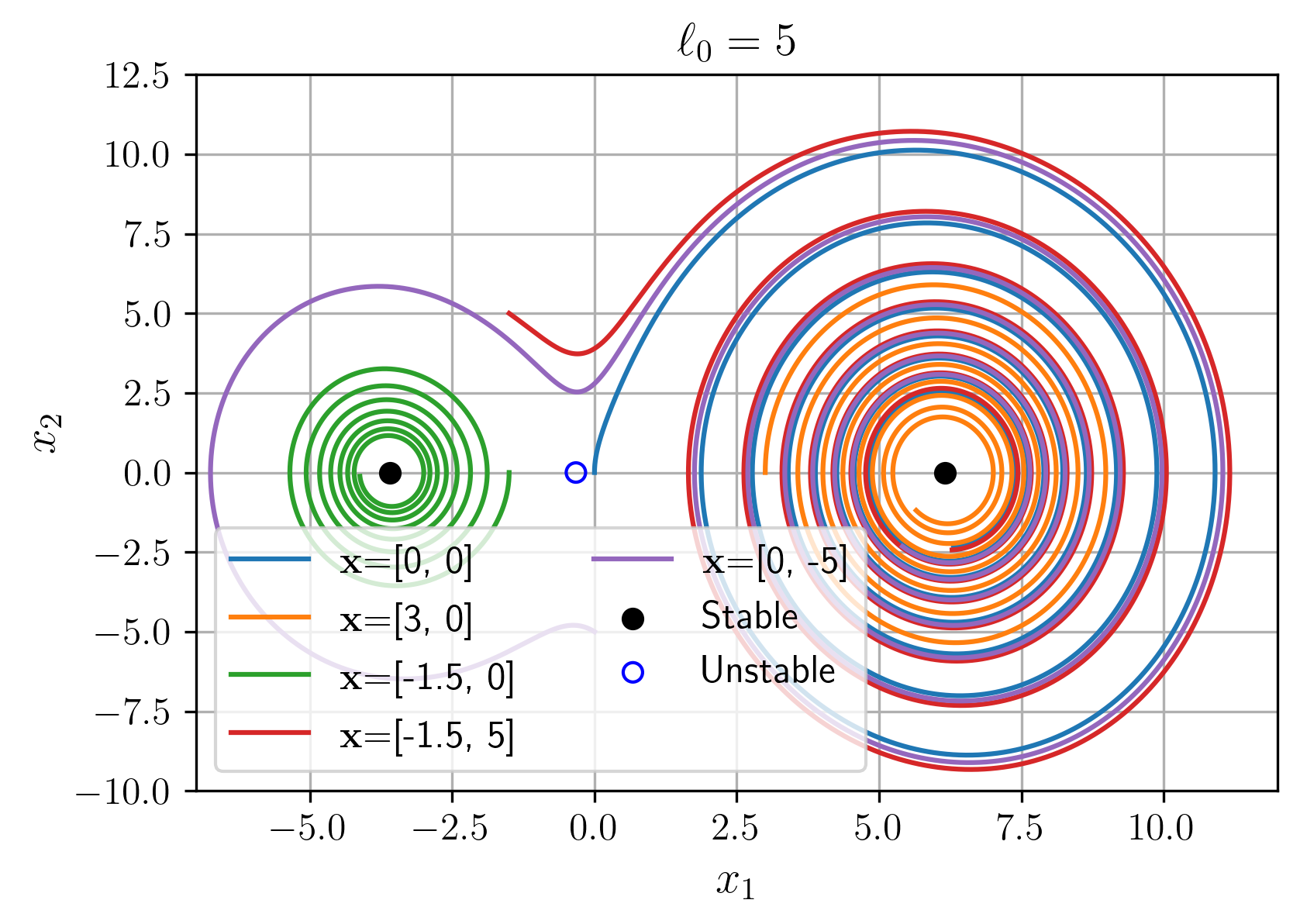
איור 5: מרחב המצב של המערכת עבור .

הערה של הבודק:

חסר תיאור איכותי של ההתנהגות הדינמית של המערכת על גבי הגרפים. לתאר שתנאי התחלה שונים מתכנסים לנקודות שיווי משקל יציבות.

שאלה 10

סעיף א’

ממשוואה (5.3):

עבור , נקודת שיווי המשקל ה”גדולה” ביותר היא , וראינו כבר שעבורה:

נגדיר משתני תיקון:

ולכן משוואת המצב לאחר לינאריזציה:

או, כמערכת משוואות:

נרצה להגיע בחזרה למשוואות תנועה, ולכן נציב במשוואה השנייה:

הגענו למשוואה מהצורה:

שהיא מערכת ברטט חופשי עם דרגת חופש אחת מסדר שני עם ריסון. נשווה מקדמים ונקבל ש:

עם תדירות ריסון:

שזה כמעט זהה לתדירות הטבעית (אם נדייק יותר בחישוב, נראה הבדל).
ראינו בהרצאה שפתרון משוואה מהצורה הזו היא:

כאשר:

עם תנאי התחלה ו- .

---

---

סעיף ב’ ו-ג’

עבור תנאי ההתחלה הנתונים:

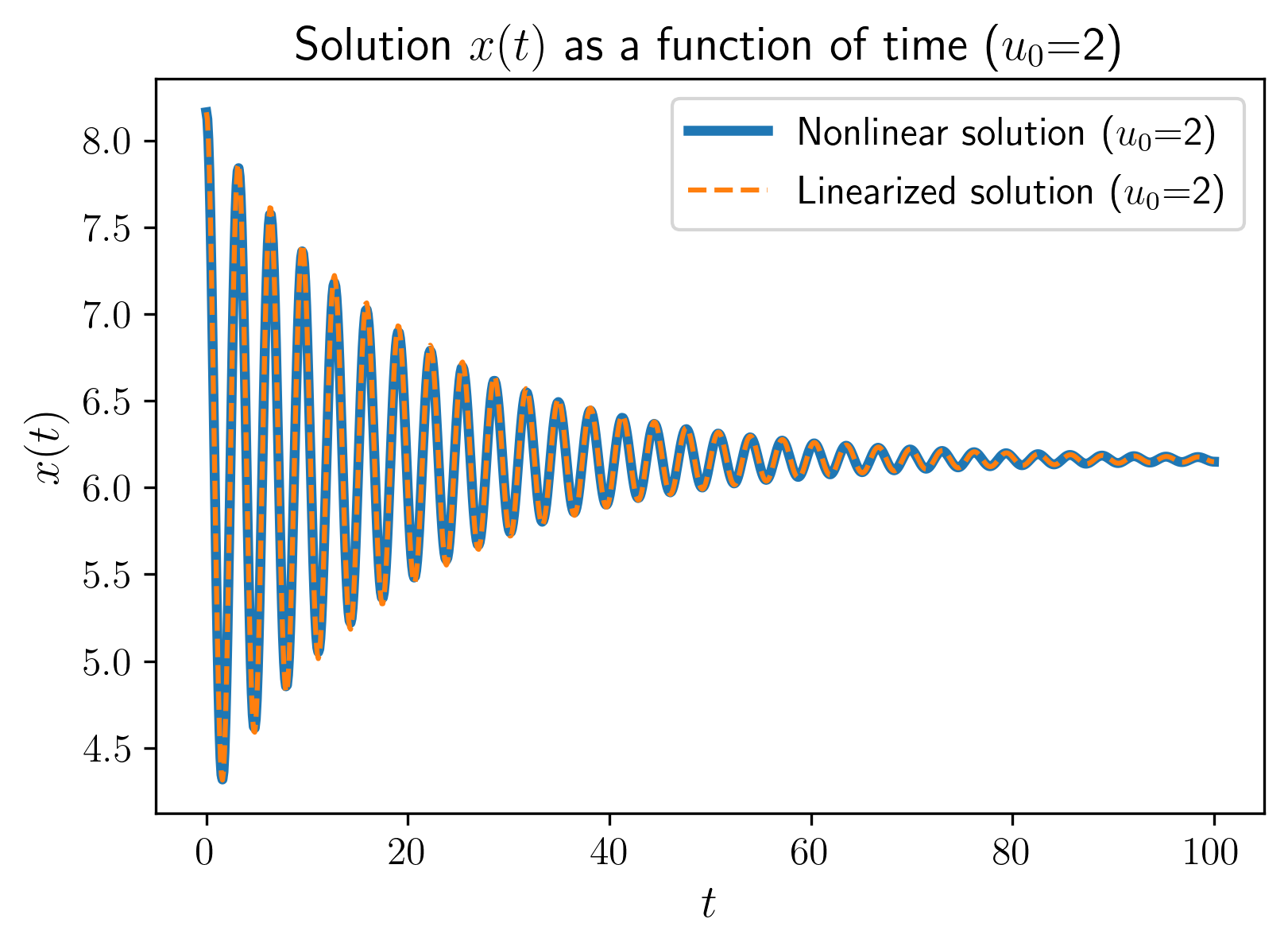
איור 6: תגובת לתנאי התחלה בקרבת שיווי המשקל.

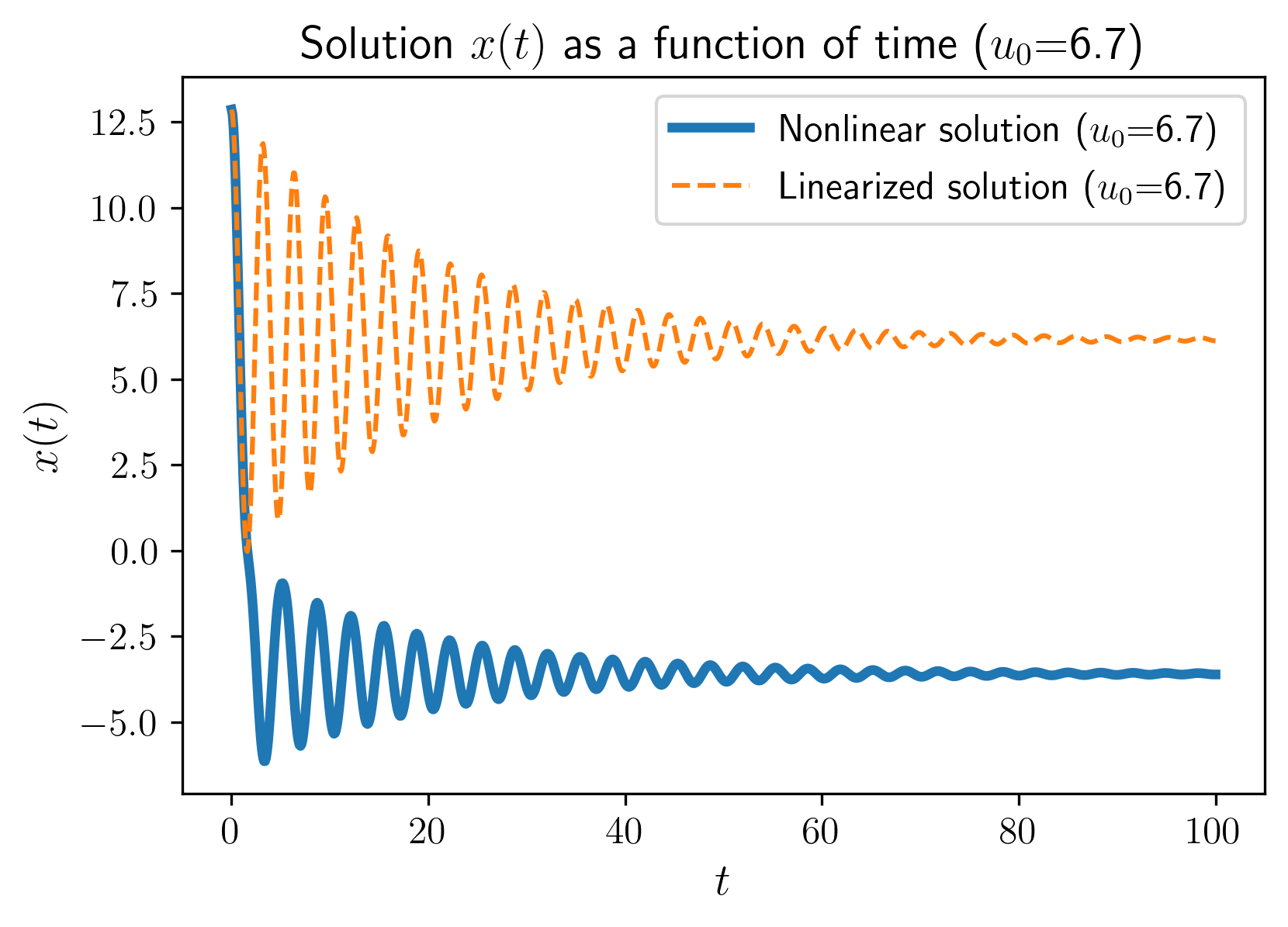
איור 7: תגובת לתנאי התחלה הרחק משיווי המשקל.

הערה של הבודק:

צריך להסביר שתוקף הלינאריזציה הוא רק בסביבה קטנה סביב הנש”מ.

שאלה 11

משוואת התנועה היא כעת:

מפני שהריסון לא לינארי לא ניתן לחשב פתרון אנליטי מדויק של התגובה. לכן נבצע מספר הנחות ונבטא את מעטפת התגובה בעזרת איזון אנרגטי.

---

---

נניח כי:

• ניתן לקרב את התגובה המרוסנת של המערכת באמצעות פונקציה סינוסואידית:
• אמפליטודת התנודות דועכת לאט - , כאשר הוא זמן מחזור ( עבור period). מה שאומר:
  $$
  \begin{aligned}
  \dot{x} & = \cancel{ \dot{A}(t)\cos ({\omega}{n}t+\phi) }-{\omega}{n}A(t)\sin({\omega}{n}t+\phi) \[1ex]
  & \approx -{\omega}{n}A(t)\sin({\omega}_{n}t+\phi)
  \end{aligned}
• תדירות המערכת המרוסנת היא בקירוב תדירות המערכת הלא מרוסנת: .

נסמן את כוח הריסון ב-:

לפי שיטת האיזון האנרגטי, העבודה שמבצע כוח הדיסיפציה במחזור אחד שווה לאיבוד האנרגיה הקינטית במחזור אחד. נסמן זמן שיא אמפליטודה כללי ב-.
ונחשב את עבודת כוח הדיסיפציה במחזור אחד, כלומר בין ל- שגם הוא בעצמו שיא:

נציב את צורת הפתרון שהנחנו:

מפני שאמפליטודת התנודות דועכת לאט נוכל להוציא אותה מתוך האינטגרל:

מאחר ואנו מבצעים אינטגרציה על פונקציה מחזורית בזמן מחזור, לפאזה אין השפעה על האינטגרל, כך שנוכל ל”התעלם” ממנה:

ננרמל את הזמן לפי זמן מחזור . נשים לב ש:

נציב באינטגרל. נזכור שכאשר אנו מחליפים משתנה באינטגרל, עלינו גם לשנות את גבולות האינטגרציה בהתאם. לפי זמן - , ולכן במשתנה זמן מנורמל (לפי הגדרת ), :

הביטוי מחליף סימן פעמיים בגבולות האינטגרציה, ומאחר והוא בערך מוחלט, נצטרך לפרק את האינטגרל:

כעת נחשב את האנרגיה הפוטנציאלית בתחילת ובסוף המחזור. בהנחה ויש נקודת קיצון ב- כללי, האנרגיה הפוטנציאלית:

נפתח את האמפליטודה לאחר זמן מחזור בטור טיילור:

הפרש האנרגיות המתקבל:

כאשר הזנחו ביטויים ממעלה שנייה ומעלה.
השינוי באנרגיה הפוטנציאלית הוא כתוצאה מעבודת הכוח הבלתי משמר. כלומר, :

נזכור ש- ולכן:

זוהי מד”ר פרידה. עם תנאי התחלה שרירותי :

נזכור שהנחנו פתרון כללי מהצורה , ולכן .

מאחר ו- :

עם תנאי התחלה הנתונים, נקבל:

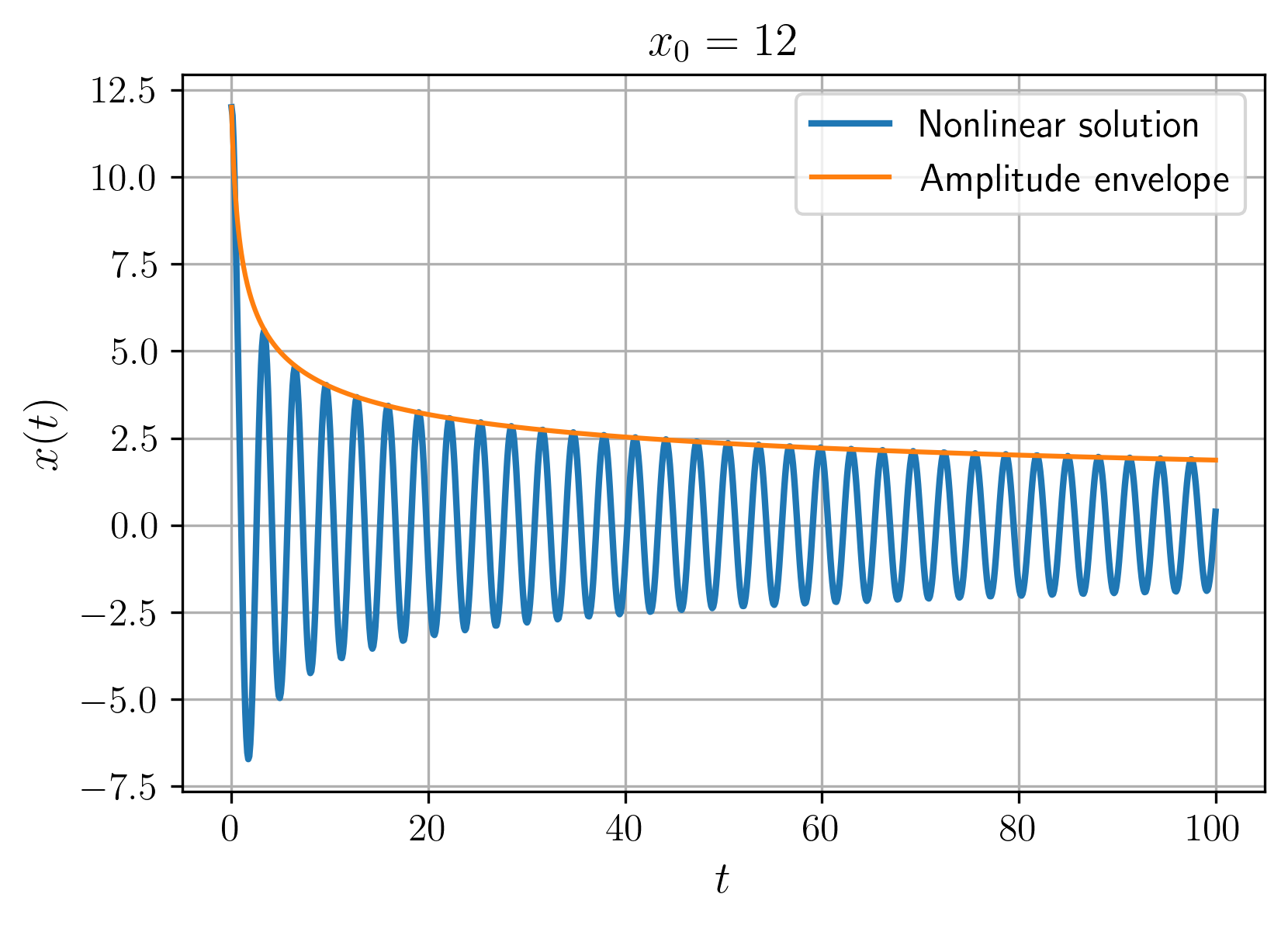
איור 8: תגובת המערכת ומעטפת התנודות עבור תנאי התחלה קרוב לנקודת שיווי משקל.

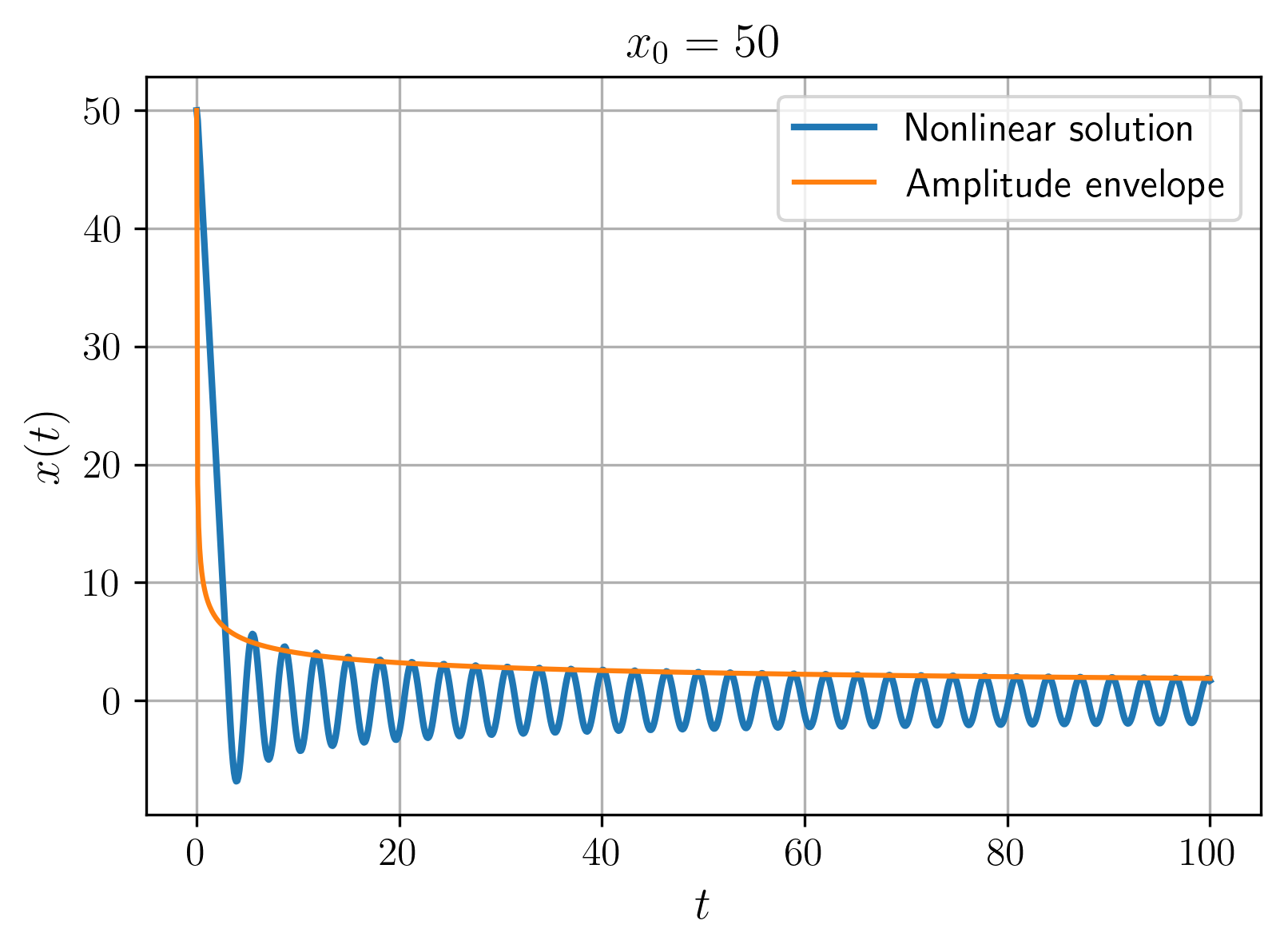
איור 9: תגובת המערכת ומעטפת התנודות עבור תנאי התחלה רחוק מהנקודת שיווי משקל.

נשים לב שבמצב מתמיד הקירוב שלנו למעטפת דעיכה די גבוה. בנוסף, עבור תנאי התחלה רחוק יותר מהשיווי משקל לוקח יותר זמן לקירוב המעטפת לעקוב אחרי הפתרון.

שאלה 12

סעיף א’

נחזור למשוואה (4.1):

נחשב את העבודה של כוחות הריסון במחזור. נסמן:

ולכן העבודה שלהם במחזור:

נניח פתרון כללי:

ולכן החזקות:

ניזכר ש- , כך שכאשר מציבים באינטגרל, גם לאחר האינטגרציה, כל הביטויים עם האקספוננטים מצטמצמים ומקבלים:

עבור הריסון הלינארי, משוואת התנועה שלנו היא:

כך שהכוח הלינארי כעת הוא:

והעבודה שלו, תחת אותו הניחוש לפתרון:

נשווה בין העבודות:

סעיף ב’

הערה:

לאחר הבהרות ושינויי הנחיות, כדי להיפטר מהעומסים והקשיחויות הלא לינאריות, אנו בונים מערכת שונה לחלוטין שכמעט ואין לה קשר למערכת המקורית, מהצורה:

בסוף הקובץ יש גם את פתרון שאלה 12 לפי המערכת המקורית, כי פתרנו אותו לפני ההבהרות, וכואב לנו מדי למחוק את הגרפים שלו.

נביא את (12.4) לצורה הבאה:

כאשר:

ולכן התדירות העצמית:

ננרמל את המערכת:

נשים לב שלפי כלל השרשרת:

---

---

נציב ונקבל:

לפי משפט תגובת התדירות, עבור מערכת לינארית, עבור כניסה תונדת נקבל יציאה תונדת, שנסמן:

נציב ב-(2.5):

נסדר:

מהשוואת מקדמים נקבל את שתי המשוואות הבאות:

כדי למצוא את תגובת התדירות, מספיק לנו למצוא את , ולכן נשווה בין הגדלים של שני צידי המשוואה:

נשים לב ש- טמון ב-, שהוא נמצא ב-, כך שלמעשה קיבלנו משוואה סתומה. נפתור אותה נומרית:

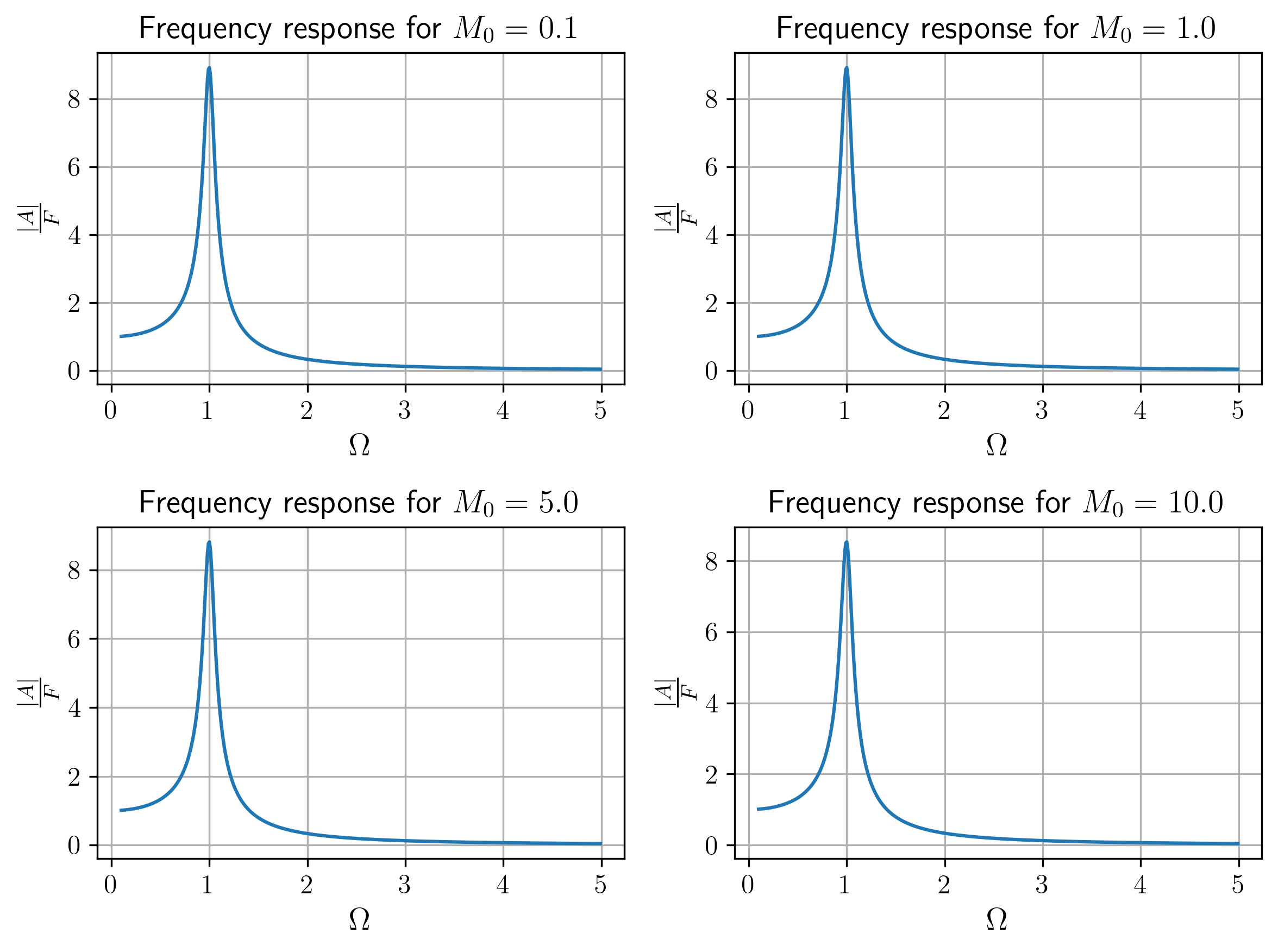
איור 10: תגובת התדירות של המערכת בריסון שקול, בתצורת יחס אמפליטודה תגובה-עומס, עבור ערכי שונים. כפי שניתן לראות, אין הבדל עבור ערכי שונים.

נשמור שני ערכים ספציפיים עבור סעיף ד’:

>>>print(f"|A|/F at omega = 0.1 * omega_n: {A_F_linearized_damping_values[M_0][0]}")
|A|/F at omega = 0.1 * omega_n: 1.0100362827339178
 
>>>print(f"|A|/F at omega = 5 * omega_n: {A_F_linearized_damping_values[M_0][-1]}")
|A|/F at omega = 5 * omega_n: 0.041829377235925426

---

---

סעיף ג’

נציב את המערכת המקורית, משוואה (2.4), ל-python:

עם התדירויות והאמפליטודות הנתונות, כך ש- :

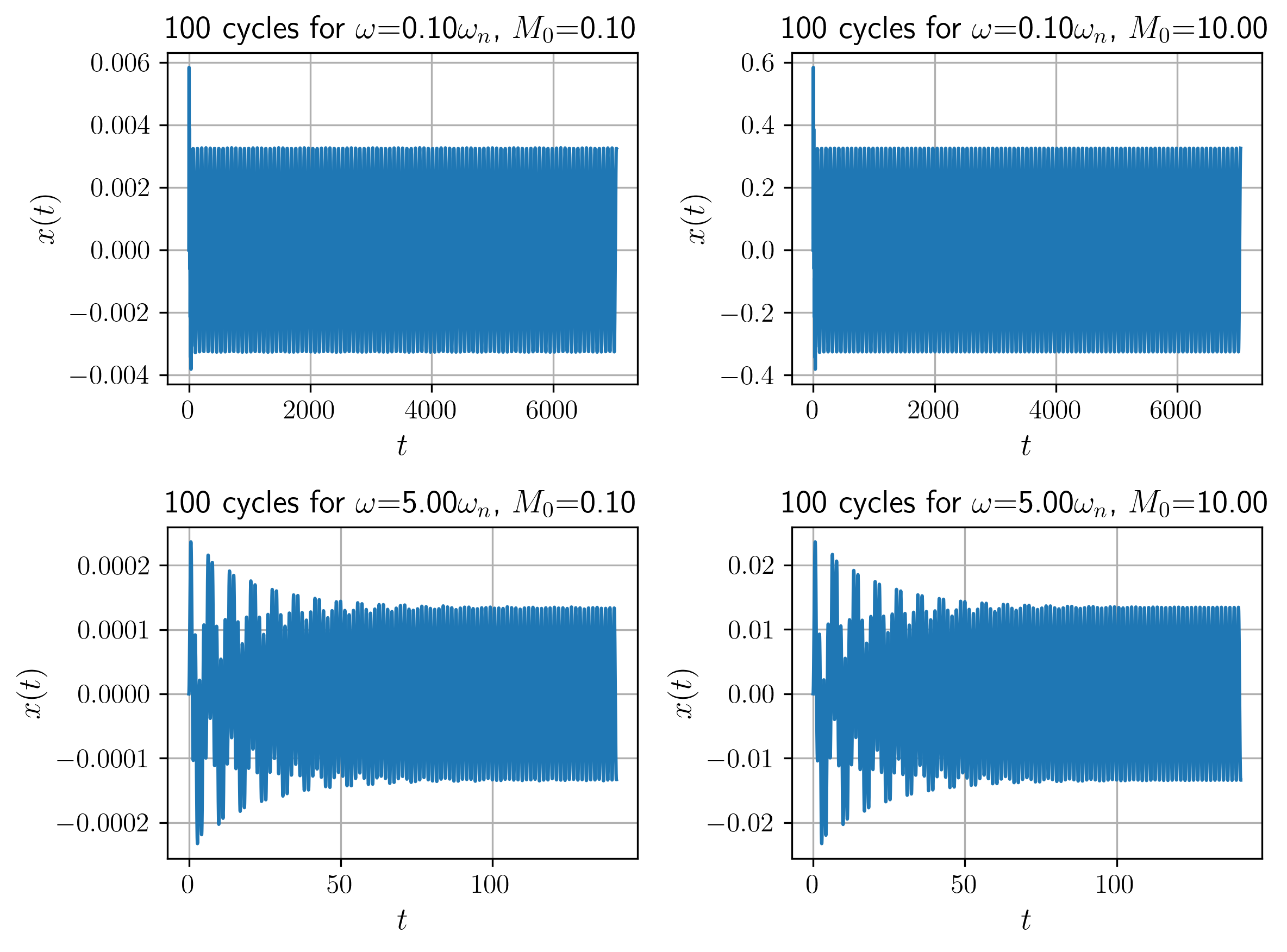
איור 11: תגובת המערכת לכניסה בתדרים ואמפליטודות שונות.

סעיף ד’

כאשר משרטטים את אות הכניסה (המומנט) ואות היציאה (המיקום) על אותו הגרף, קשה לנו לראות את היחסים ביניהם מאחר והם בסקאלות שונות לגמרי. לכן ננרמל את אות הכניסה כדי שנוכל להשוות ביניהם יותר בקלות:

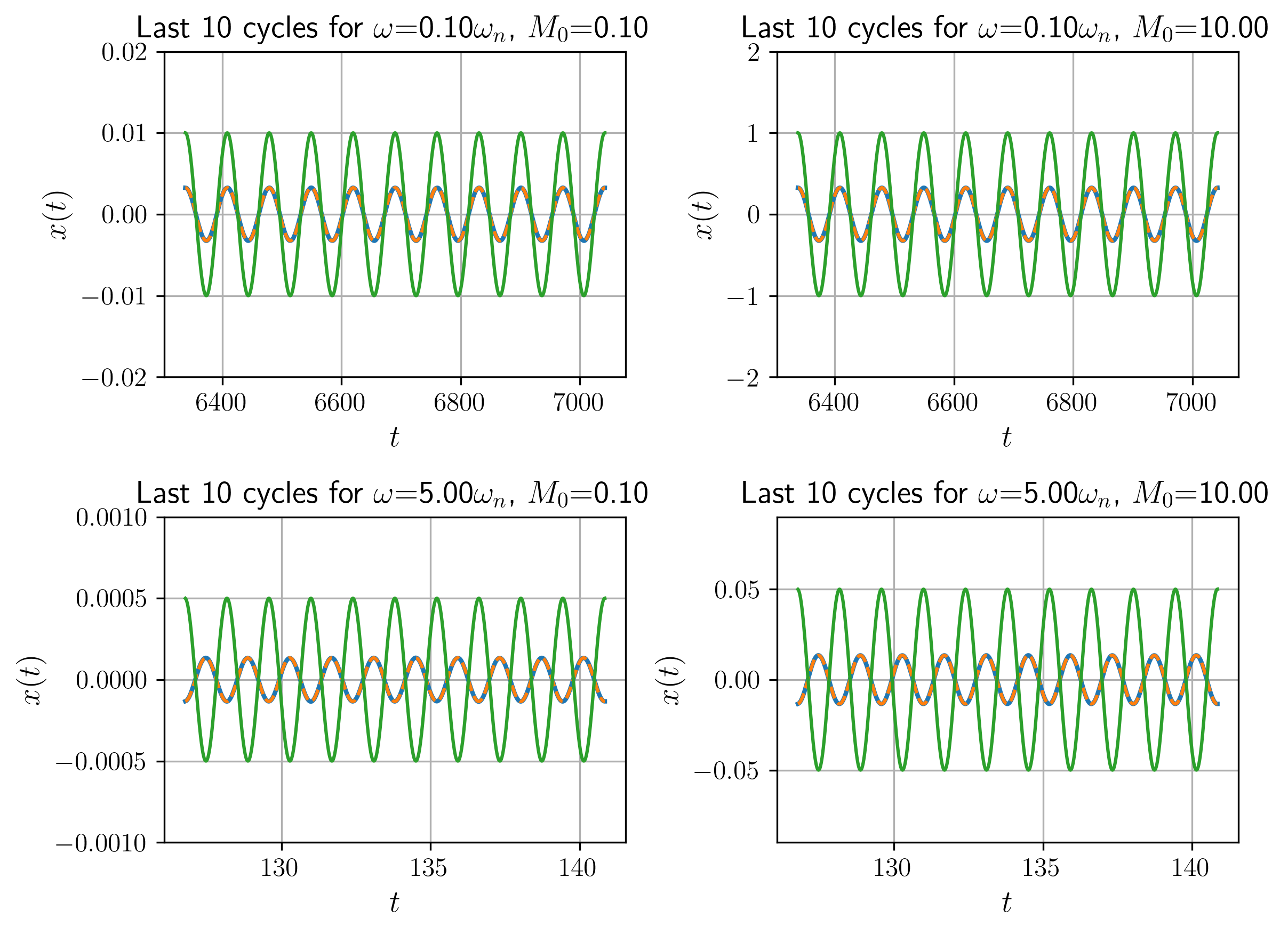
איור 12: תגובת המערכת לכניסה בתדרים ואמפליטודות שונות, לאחר 90 מחזורים, מול מומנט תונד (מנורמל על הגרף), וה-fitting שלו לפי least_squares. נשים לב שקנה המידה של הגרפים שונה אחד מן השני.

נשים לב שעבור תדרים נמוכים מהתדירות הטבעית, אין הפרש פאזות בין האות כניסה ויציאה, לעומת תדרים גבוהים מהתדירות הטבעית, בהם הפרש הפאזות גדל ל-.

מבחינה מספרית:

for i, omega in enumerate(omega_values):
	for i, omega in enumerate(omega_values):
	for j, M_0 in enumerate(M_0_values):
		print(f'For omega={omega_values_coeff[i]:.2f}*omega_n and M_0={M_0:.2f}:')
		print(f'\t Amplitude ratio (A/F): {A_F}')
		print(f'\t Phase difference: {np.degrees(phi_fit)} degrees')

---

---

מקבלים:

For omega=0.10*omega_n and M_0=0.10:
	 Amplitude ratio (A/F): 1.0099655530879943
	 Phase difference: 0.6478363765490998 degrees
For omega=0.10*omega_n and M_0=10.00:
	 Amplitude ratio (A/F): 1.0100211925434814
	 Phase difference: 0.6491503151199068 degrees
For omega=5.00*omega_n and M_0=0.10:
	 Amplitude ratio (A/F): 0.04149179688018125
	 Phase difference: 178.70857247041326 degrees
For omega=5.00*omega_n and M_0=10.00:
	 Amplitude ratio (A/F): 0.04165029257060937
	 Phase difference: 178.66486193945272 degrees

שזה בקירוב מאוד טוב לחישוב המערכת בריסון שקול בסעיף ב’.

סעיף ה’

כאשר נחשב נומרית את עבור ערכי שונים אנו מקבלים גרפים זהים, מה שמוכיח ש- לא תלוי ב- עצמו:

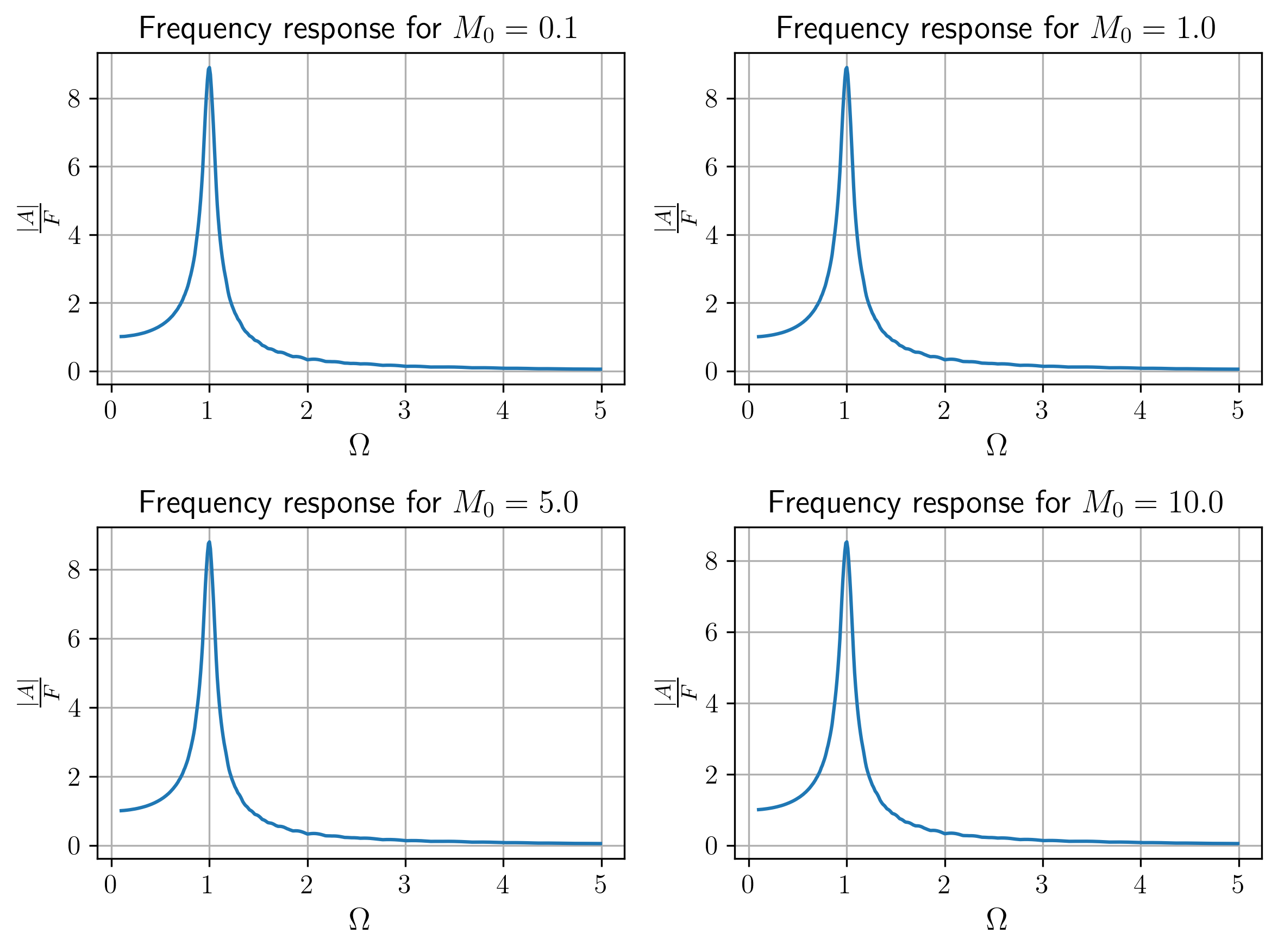
איור 13: תגובת תדירות של המערכת המקורית עבור ערכי שונים (חושב נומרית).

---

---

כעת נשווה את אחד מהפתרונות הנומריים (שהראינו שהם זהים) לאנליטי של הלינאריזציה:

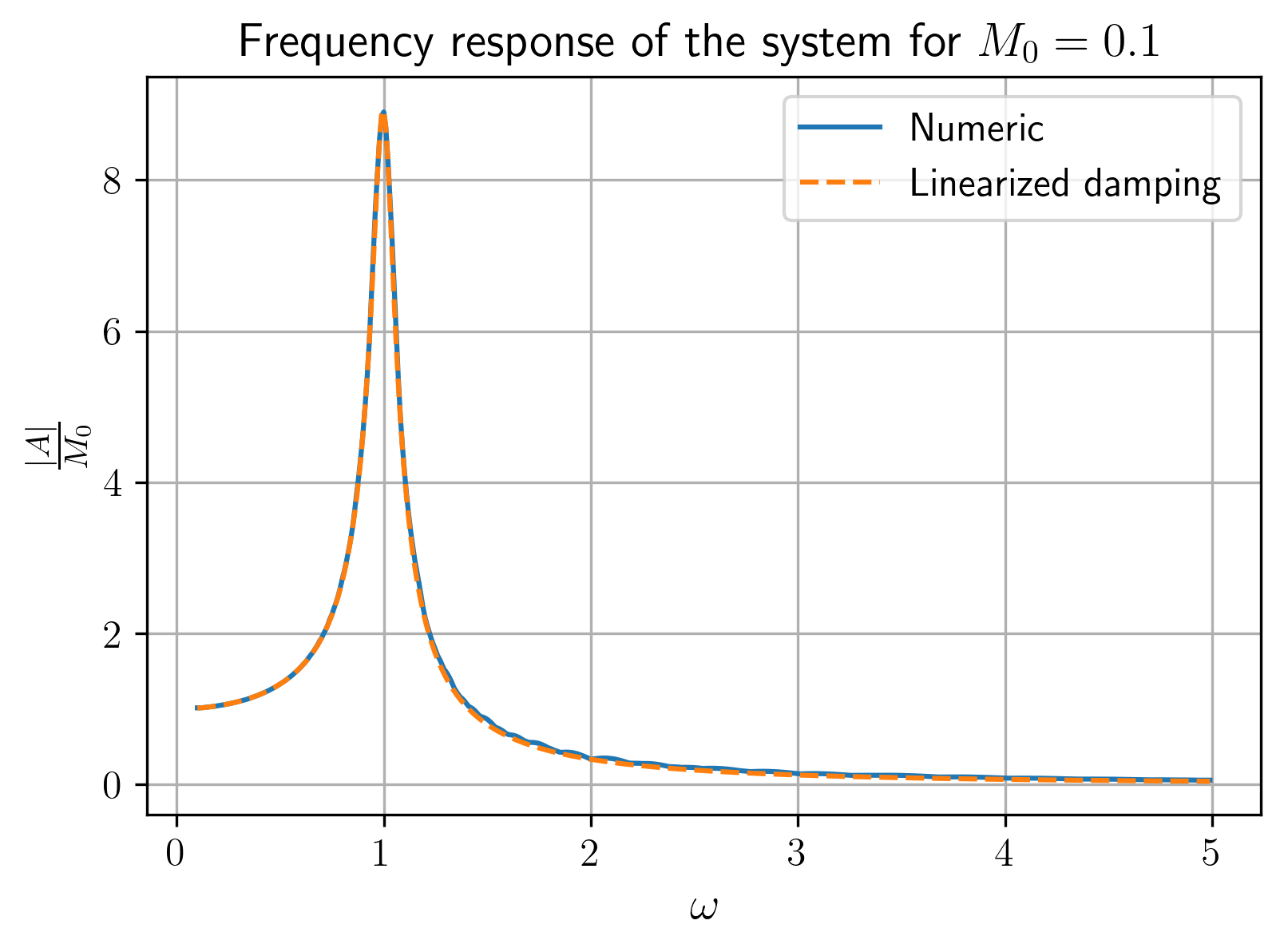
איור 14: תגובת התדירות של המערכת בשיטה אנליטית אל מול שיטה נומרית.

הערה של הבודק:

חסר הסבר למה יש התאמה טובה. צריך להגיד שהקירוב על ידי ריסון שקול לא גורם לשינוי בתגובה בהשוואה למערכת הלא לינארית בגלל שאי הלינאריות במערכת היא על המהירות (ריסון) וזה לא אמור להשפיע על מחזוריות התנועה.

שאלה 13

במהלך התרגיל ניתחנו מערכת דינמית בעלת דרגת חופש אחת. מצאנו כי עבור ערכים שונים של , המייצגים תכונות שונות של אורך הקפיץ, מתקבל מספר שונה של נקודות שיווי משקל, אשר להן תכונות שונות.

הראינו באמצעות ביטוי אנליטי של מעטפת ההתכנסות כי כאשר המערכת מתקרבת למצב המתמיד, המעטפת עוטפת את הגרף בדיוק גבוה. בנוסף, מצאנו שככל שתנאי ההתחלה גדולים יותר, לוקח למעטפת זמן רב יותר “לעטוף” את הגרף.

לאחר מכן, ניתחנו את תגובת המערכת בזמן באמצעות שיטה אנליטית שכללה לינאריזציה סביב נקודת שיווי המשקל היציבה הימנית, וכן באמצעות חישוב נומרי. מהניתוח עלתה תוצאה מעניינת: קיימת התאמה טובה מאוד בין הקירוב הלינארי לבין התנהגות המערכת הלא לינארית המקורית. כלומר, ניתן לחזות את הגבר המערכת ואת תדר הרזוננס באופן אנליטי בקירוב מדויק מאוד.

---

---

שאלה 12 לפי המערכת המקורית

סעיף ב’

נחזור ללינאריזציה של המערכת ממשוואה (5.3):

כעת, עם המומנט, המשוואה הופכת להיות:

ולכן נצטרך לחשב גם את:

כך שמשוואת המצב לאחר לינאריזציה (עם תיקון ו-):

נחזור למשוואה אחת, כאשר נקרא למרסן הלינארי שלנו :

אנו יודעים ש- :

לפי משפט תגובת התדירות, עבור מערכת לינארית, עבור כניסה תונדת נקבל יציאה תונדת, שנסמן:

נציב ב-(2.4):

נסדר:

מהשוואת מקדמים נקבל את שתי המשוואות הבאות:

כדי למצוא את תגובת התדירות, מספיק לנו למצוא את , ולכן נשווה בין הגדלים של שני צידי המשוואה:

יהיה לנו יותר נוח אם נציג את הקשר במונחים של :

כעת נוכל להציג את כתלות ב- (כמובן, נציב את (2.3) עבור ):

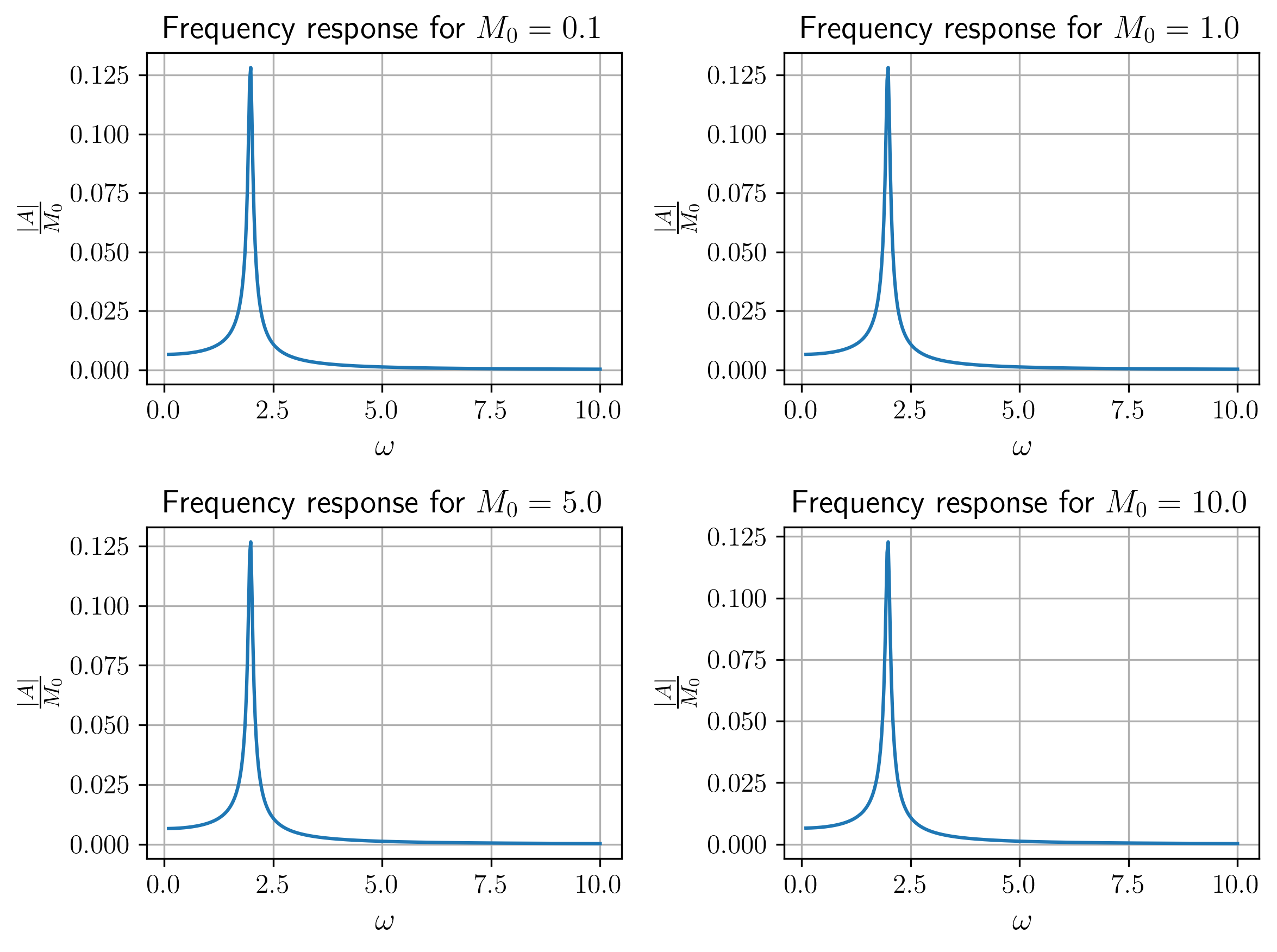
איור 10: תגובת התדירות של המערכת בריסון שקול, בתצורת יחס אמפליטודה תגובה-עומס, עבור ערכי שונים. כפי שניתן לראות, אין הבדל עבור ערכי שונים.

נשמור שני ערכים ספציפיים עבור סעיף ד’:

>>>print(f"|A|/M0 at omega = 0.2: {calculate_A_M0(0.2)}")
|A|/M0 at omega = 0.2: 0.006702698492621046
 
>>>print(f"|A|/M0 at omega = 10: {calculate_A_M0(10)}")
|A|/M0 at omega = 10: 0.0002670822089080033

סעיף ג’

נציב את המערכת המקורית, משוואה (4.1), ל-python:

עם התדירויות והאמפליטודות הנתונות, כך ש- :

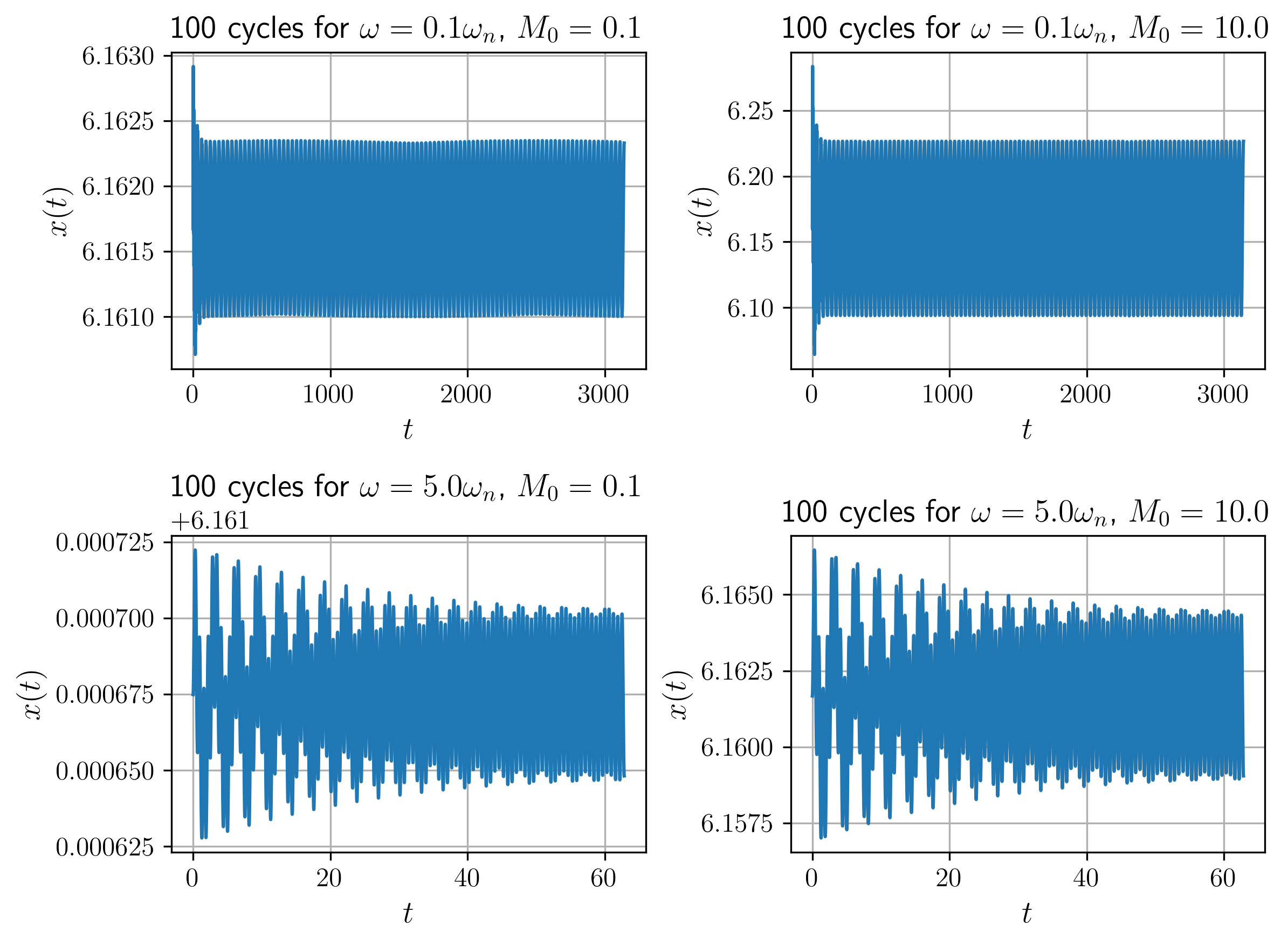
איור 11: תגובת המערכת לכניסה בתדרים ואמפליטודות שונות.

סעיף ד’

כאשר משרטטים את אות הכניסה (המומנט) ואות היציאה (המיקום) על אותו הגרף, קשה לנו לראות את היחסים ביניהם מאחר והם בסקאלות שונות לגמרי. לכן ננרמל את אות הכניסה כדי שנוכל להשוות ביניהם יותר בקלות:

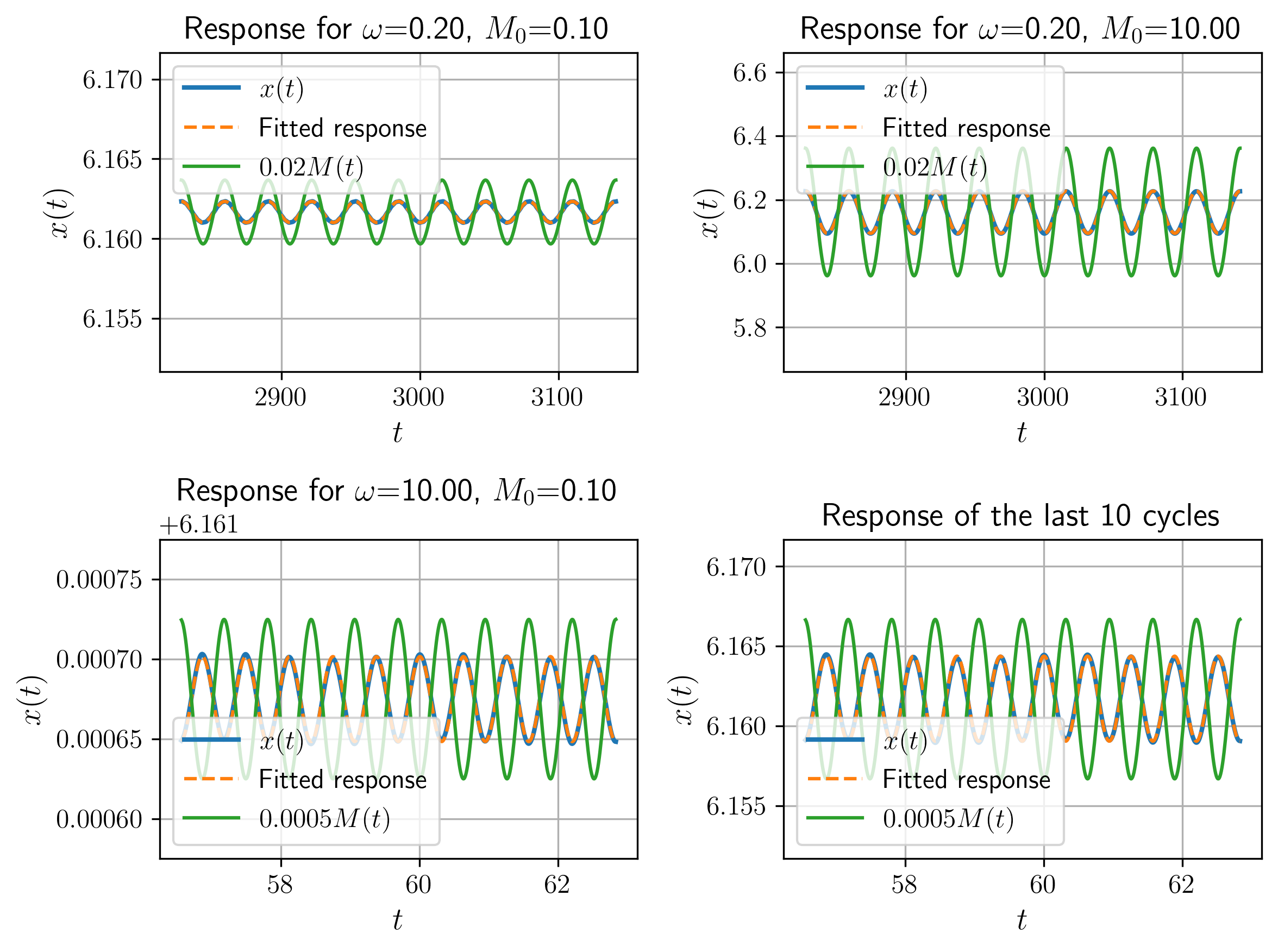
איור 12: תגובת המערכת לכניסה בתדרים ואמפליטודות שונות, לאחר 90 מחזורים, מול מומנט תונד (מנורמל על הגרף), וה-fitting שלו לפי least_squares. נשים לב שקנה המידה של הגרפים שונה אחד מן השני.

נשים לב שעבור תדרים נמוכים מהתדירות הטבעית, אין הפרש פאזות בין האות כניסה ויציאה, לעומת תדרים גבוהים מהתדירות הטבעית, בהם הפרש הפאזות גדל ל-.

מבחינה מספרית:

for i, omega in enumerate(omega_values):
	for i, omega in enumerate(omega_values):
	for j, M_0 in enumerate(M_0_values):
		print(f'For omega={omega:.2f} and M_0={M_0:.2f}:')
		print(f'\t Amplitude ratio: {A_M_0}')
		print(f'\t Phase difference: {np.degrees(phi_fit)} degrees')

מקבלים:

For omega=0.20 and M_0=0.10:
	 Amplitude ratio: 0.00661754644197189
	 Phase difference: 0.2939081953482851 degrees
For omega=0.20 and M_0=10.00:
	 Amplitude ratio: 0.006621729676823907
	 Phase difference: 0.29643422974609185 degrees
For omega=10.00 and M_0=0.10:
	 Amplitude ratio: 0.0002663148823770744
	 Phase difference: -179.94939249219144 degrees
For omega=10.00 and M_0=10.00:
	 Amplitude ratio: 0.0002664909436133994
	 Phase difference: 179.4341257792274 degrees

שזה בקירוב מאוד טוב לחישוב המערכת בריסון שקול בסעיף ב’.

סעיף ה’

כאשר נחשב נומרית את עבור ערכי שונים אנו מקבלים גרפים זהים, מה שמוכיח ש- לא תלוי ב- עצמו:

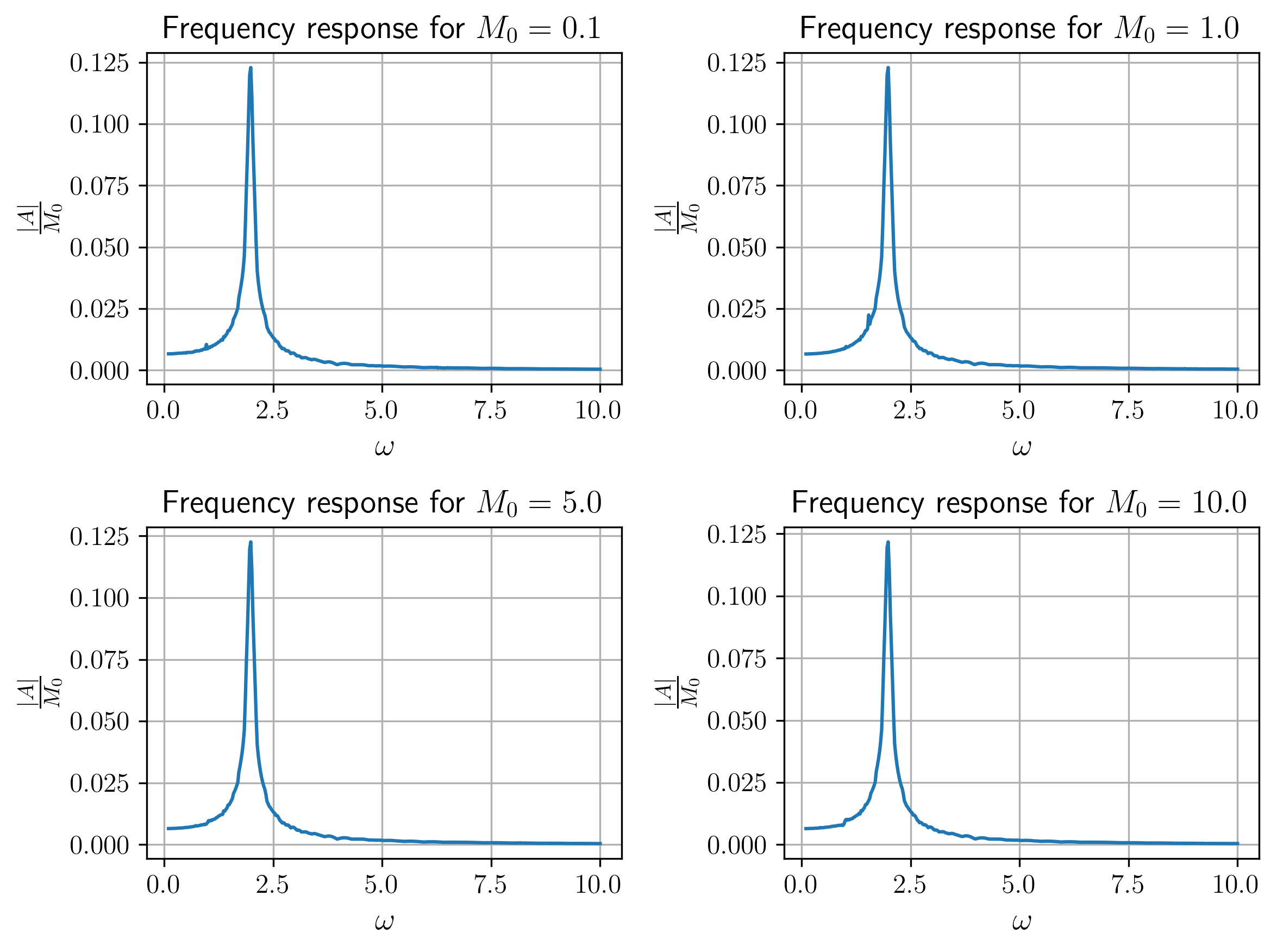
איור 13: תגובת תדירות של המערכת המקורית עבור ערכי שונים (חושב נומרית).

כעת נשווה את אחד מהפתרונות הנומריים (שהראינו שהם זהים) לאנליטי של הלינאריזציה:

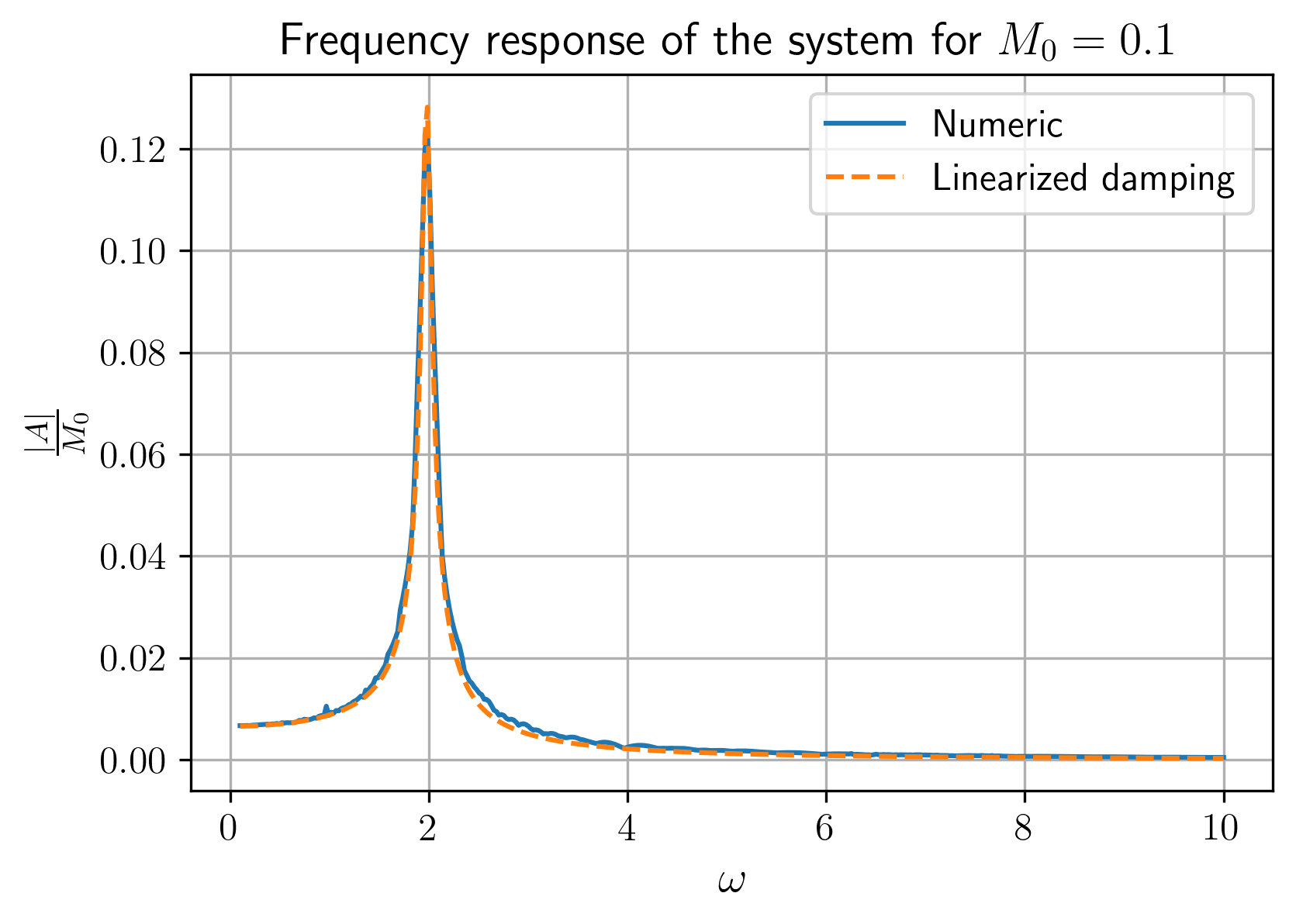
איור 14: תגובת התדירות של המערכת בשיטה אנליטית אל מול שיטה נומרית.