פנגייה

CAL1_006 פולינום טיילור

• זמן קריאה: 8 דק'

טיילור

הקדמה:
פולינום טיילור בא לפתור את הבעיה של חישוב ערך של פונקציות “מסובכות”, בעזרת חישוב ערך של פולינום שמאוד דומה לפונקציה.
למשל, עבור הפונקציה , איך נוכל לחשב את ערכה ב-? מה לגבי הערך ?
נתחיל בדוגמה פשוטה, ולאט לאט נכליל אותה משלב לשלב עד שנקבל אלגוריתם כללי.

אם גזירה אז המשיק ב- הוא:

למשל, עבור הפונקציה :

ולכן המשיק ל- בנקודה הוא .
book
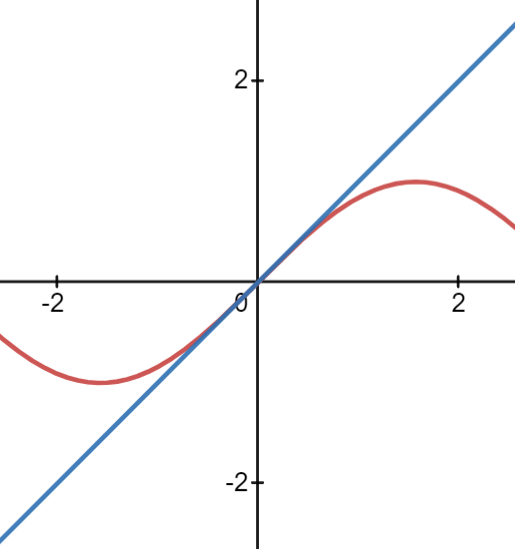
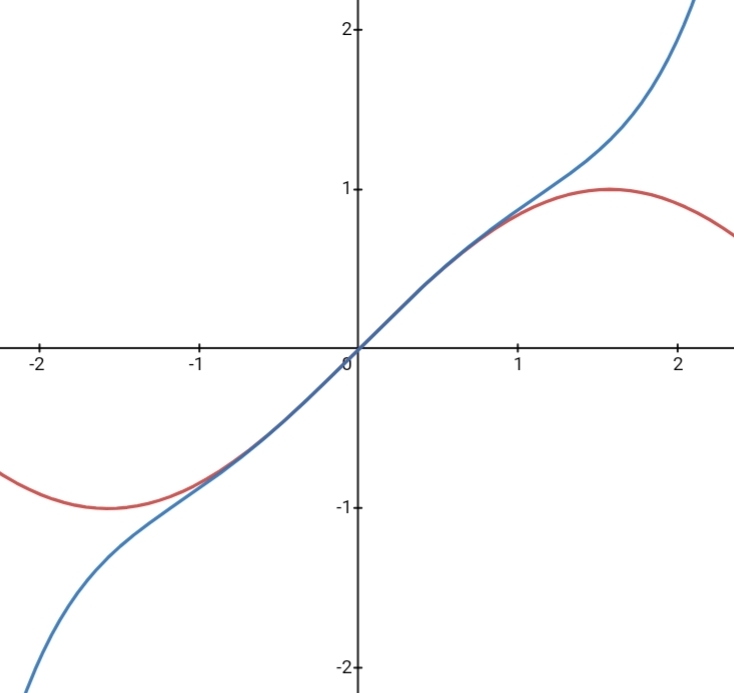
ניתן לראות כי ליד נקודת ההשקה , ערכי הפונקציה והמשיק מאוד קרובים אחד לשני. בכתיב מתמטי, ההפרש בין הפונקציה למשיק:

ההפרש בין הפונקציה למשיק שואף ל- כאשר . אבל יותר מזה:

כלומר, ההפרש בין למשיק שואף ל- “יותר מהר” מאשר שואף ל-.
לכן קוראים למשיק קירוב לינארי של ליד .
נביט בנקודה :

0.707 .. .=\frac{\sqrt{ 2 }}{2}=\sin \frac{\pi}{4}=f\left( \frac{\pi}{4} \right)\approx y\left( \frac{\pi}{4} \right)= \frac{\pi}{4}=0.785.. . $$ הקירוב הלינארי שלנו, $y(x)$, אמנם לא מדויק, אבל כן יחסית קרוב לערך שרצינו למצוא, שהוא $\sin \frac{\pi}{4}$. נחזור לדוגמתנו $\sin x$. הפעם לא נשתמש בקירוב לינארי, אלא [[ALG1_002 פולינומים#פולינום|בפולינום]] $x-\frac{x^{3}}{6}$: ![[Pasted image 20221227152423.png|book|400]] עבור הנקודה $x=\frac{\pi}{4}$:

0.707.. .=\sin \frac{\pi}{4}\approx y\left( \frac{\pi}{4} \right)=\frac{\pi}{4}-\frac{\left( \frac{\pi}{4} \right)^{3}}{6}=0.705.. .
$$

קירוב זה הרבה יותר טוב מאשר הקירוב הלינארי.

באופן כללי, משוואת המשיק של בנקודה היא:

נחשב את ההפרש:

נוכל לכתוב:

נסמן , וכעת, נכתוב את (2) כך:

בנוסף, נשים לב כי לפי (1), מתקיים:

כלומר, הכללנו את מה שמצאנו על לכל פונקציה גזירה - הישר המשיק לפונקציה בנקודה הוא קירוב לינארי של הערך של הפונקציה בסביבה של נקודה זו. ראינו גם כי קירוב לינארי זה הוא לא בהכרח מדויק. קירוב יותר טוב שמצאנו הוא פולינום.
אז, נרצה למצוא פולינום שמחליף את משוואת המשיק, , במשוואה שקיבלנו ב-(3).

נראה איך הגענו לפולינום . נזכור שמטרתנו למצוא פולינום כמה שיותר דומה ל- בסביבה .
נתחיל בפולינום ממעלה כללי:

אנו יודעים כי עבור :

אנו רוצים ש- יהיה כמה שיותר דומה ל- ולכן נדרוש שיתקיים :

בנוסף, מתקיים:

כלומר, ערך הנגזרת של ב- הוא . נדרוש זאת גם על הפולינום שלנו, הרי אם עולה ב- נרצה שגם הפולינום שלנו יעלה ב-:

נמשיך להשוות בין הנגזרות של ו- בנקודה (כי הפולינום יהיה יותר דומה ל- ככל שיותר ויותר הנגזרות שלהן יהיו דומות):

מההשוואה נקבל:

בסה”כ, קיבלנו את הפולינום:

הערות:

  1. בכל גזירה, מצאנו ערך של מקדם אחר. באופן יותר כללי, עבור הגזירה ה-, מצאנו את ערכו של המקדם ה-, שהוא .
  2. נשים לב, שאם היינו מתחילים מפולינום ממעלה , פשוט היינו מקבלים קבוע, ואם היינו מתחילים מפולינום ממעלה , היינו מקבלים את הישר המשיק, - הקירוב הלינארי הראשון שלנו.
  3. אם היינו מתחילים אפילו מפולינום ממעלה , היינו מקבלים קירוב אפילו יותר טוב:

book
3. ככל שאנחנו משפרים את הקירוב שלנו, מקדמי הפולינום הראשונים נשמרים:

  1. אנו מקבלים פולינום שהוא קירוב של הפונקיצה אך ורק בסביבה של הנקודה! למשל, ב הפולינום שקיבלנו כבר לא קירוב טוב.
  2. פעולת העצרת חוזרת על עצמה כאן, מהסיבה הפשוטה שכאשר גוזרים פולינום שוב ושוב, אנו מכפילים את החזקה במקדם, שתמיד יהיה .
  3. כדי לבודד את המקדם , אנו גזרנו את הפולינום פעמים - ובכך נפטרנו מכל המקדמים . בנוסף, הצבנו בנגזרת ובכך נפטרנו מכל המקדמים .

נכליל למקרה בו הוא לא בהכרח . נסמן .

הכיוון שאנו חותרים אליו הוא כזה:
נניח כי גזירה פעמים ב-. נרצה למצוא פולינום ממעלה לכל היותר שנסמנו שמקיים:

אבל עכשיו, אם למשל נבחר פולינום ממעלה : , כאשר נגזור אותו נקבל ערכים שקשה לעבוד איתם בנקודה :

לעומת הדוגמאות הקודמות, לא ניתן לחלץ מהו הערך של כל אחד מהמקדמים בכל שלב של הגזירה.

לכן נבחר בפולינום מצורה קצת שונה:

כעת, כאשר נציב בפולינום, ואפילו בנגזרות הפולינום , נקבל כי כל הביטויים מהצורה ייתאפסו ויפרידו לנו מקדם אחד ויחיד שנוכל להשוות לנגזרת של הפונקציה.

פיתוח פולינום לפולינום מהצורה

משפט:

יהי פולינום ממעלה לכל היותר, יהי מספר. אז קיימים מספרים יחידים עבורם:

ובנוסף, לכל מתקיים:

הוכחה:
נסמן . אזי:

לאחר פתיחת סוגריים עם נוסחת הבינום של ניוטון, קיימים כך ש:

לכל נסמן .
המחשה: עבור : . אזי:

בהכללה:

אז נוכל לרשום:

כעת נחפש פולינום ממעלה לכל היותר עבורו:

פולינום טיילור

הגדרה:

תהי פונקצייה הגזירה פעמים ב-. פולינום טיילור מסדר סביב /ב- הוא:

אזי, למשל עבור , מתקיים , ועבור , מתקיים , שזהו בעצם הישר המשיק, הקירוב הלינארי הראשוני שלנו.
כאשר אז הוא נקרא פולינום מקלורין:

השארית מסדר היא:

הערות:

  1. המרחק בין הוא
  2. פולינום טיילור מסדר סביב הוא הפולינום היחיד עבורו:

ההפרש בין פונקציה לפולינום טיילור שלה שואף ל- “ממש מהר”

משפט:

נניח כי גזירה פעמים ב-. אזי:

הוכחה בהמשך

רשימה של פולינומי מקלורין של כמה פונקציות:

  1. עבור :
  2. עבור :
  3. עבור:
  4. עבור: זהו סכום של סדרה הנדסית ולכן אם :
  5. עבור:
    אפשר להראות כי . לכן:

משפט טיילור

משפט:

נניח כי גזירה פעמים () בקטע , ויהי . אז לכל קיים הנמצא ממש בין ו- ( או ) עבורו:

לשארית אנו קוראים שארית לגראנז’.

הערות:

  1. המספר תלוי ב-.
  2. מתקיים:
  1. עבור , גזירה ב-, , אז קיים עבורו:

קיבלנו את משפט לגראנז’:

דוגמאות:

  1. מצאו מספר רציונלי (מפורש) עבורו .

ננסה :

ננסה :

ננסה :

אז:

תרגילים:

  1. חשבו את בקירוב של .
    נביט בפונקציה . נפתח טיילור עבור הנקודה . קיים כך ש: לא מספיק.
    ננסה : כלומר מספיק.
    לכן:

אם הנגזרת ה- חסומה, אז הפולינום טיילור שואף לפונקצייה

משפט:

נניח כי גזירה מכל סדר בכל נקודה של קטע ונניח כי קיים כך שלכל ולכל מתקיים . יהי .
אז לכל מתקיים כי:

הוכחה:
יהי . אם ברור. אם אז לפי טיילור קיים הנמצא ממש בין עבורו:

(סנדוויץ’)

דוגמאות:

  1. עבור :

לכן , לפי המשפט, לכל :

באופן דומה עבור .

עמודים המציינים את העמוד הזה