DYN1_HW005 תרגיל בית 5

	סטודנט א’	סטודנט ב’
שם	עידו פנג בנטוב	ניר קרל
ת”ז	CLASSIFIED	CLASSIFIED
דואר אלקטרוני	CLASSIFIED	CLASSIFIED

תרגיל 1

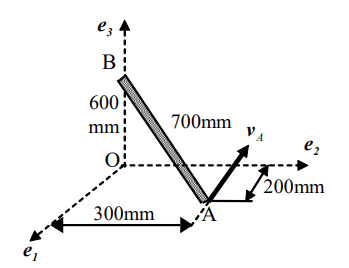
סכימת החוליה

נניח כי המצב המתואר באיור הוא ב- .

לפי חישוב קצב סיבוב, אנו יכולים למצוא רק את המהירות הזוויתית הניצבת של . היא נתונה ע”י:

וקטורי המיקומים:

וקטור המיקום :

נגזור (אפילו לא צריך את כלל האופרטור כי אנחנו במערכת צירים קבועה):

נציב בביטוי למהירות הזוויתית:

נציב את הנתונים ():

ממשוואות גוף קשיח אנו יודעים כי נציב ונקבל:

משוואה זו נכונה בכל רגע, בפרט ב- :

נציב נתונים ונקבל:

נציב בחזרה בביטוי ל-:

תרגיל 2

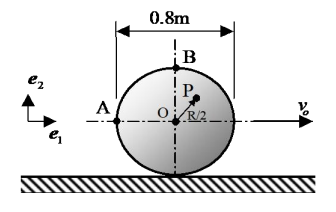
סכימת הדסקה

סעיף א’

ממשוואות גוף קשיח:

מאחר והדסקה מתגלגלת ללא החלקה, נסיק ש:

כאשר היא מהירות מרכז הדסקה, ו- הוא המהירות הזוויתית של הדסקה. אנו במקרה המישורי, ולכן נוכל גם להסיק ש:

נגדיר את בזווית מהכיוון החיובי של . לכן:

מהירות נתונה כ- .
נציב הכל בביטוי ל-:

נציב נתונים ונקבל:

סעיף ב’

ממשוואות גוף קשיח:

ניתן לראות כי . נציב גם את מסעיף קודם ונקבל:

נציב נתונים ונקבל:

תרגיל 3

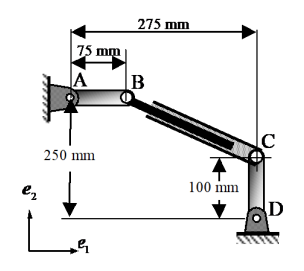
סכימת המפרק הטלסקופי

הערה:

תאכלס תאכלס תאכלס, התעלמתי מהעובדה ש- הוא מפרק טלסקופי, אבל הכל טוב, אפשר להראות ע”י פיתוח (דרישה שהמהירות היחסית בין שני המפרקים בכיוון הניצב היא אפס) שזה יוצא בול אותו הדבר.

במקרה המישורי, אנו יודעים ש:

וקטור מיקום הרגעי :

גודלו (שנשאר קבוע):

את נמצא ממהירות ו- בנפרד. ממשוואות גוף קשיח:

לכן:

נציב בביטוי ל-:

קיבלנו:

תרגיל 4

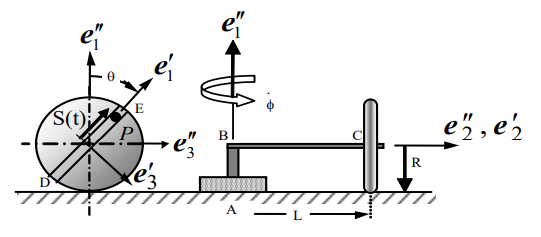
סכימת הדסקה

נגדיר את מערכות הצירים אחת ביחס לשנייה:

סעיף א’

מערכת צמודה לדסקה, ולכן:

נייצג במערכת :

סעיף ב’

אם רגעית , זה לא בהכרח אומר ש- מתאפסת. לכן, עלינו למצוא מהי .
ממשוואות גוף קשיח, מהירות נקודה :

נסמן ב- ו- את נקודת ההשקה בין הדסקה לרצפה, בהתאמה. מאי החלקה נסיק ש- . מקשרי גק”ש על הדסקה:

נשווה בין שני הביטויים ל-:

לכן, מסעיף א’:

נציב נתונים ונקבל:

סעיף ג’

נשים לב שהביטוי:

הוא למעשה גם המהירות הזוויתית של מערכת הצירים . לכן, נוכל לייצג את נקודה במערכת זו ולגזור לפי כלל האופרטור. מיקומו:

לפי כלל האופרטור:

נבנה טבלה:

נקבל:

סעיף ד’

נגזור שוב לפי כלל האופרטור, כאשר נשים לב ש- . בנוסף, למען פישוט הבעיה, נציב את הנתונים כדי להסיק ש- (וגם כמובן ש- ):

נקבל:

תרגיל 5

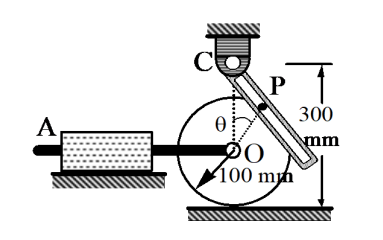
סכימת הגלגל

אנו במקרה מישורי, ולכן נוכל למצוא את המהירות הזוויתית לפי:

כאשר היא נקודת ההשקה הגאומטרית על המוט המחורץ עם הנקודה שעל הגלגל.
נגדיר מערכת צירים קבועה:

סכימת הגלגל, אבל יותר ברור

נשים לב לקצת גאומטרייה בשביל גדלים שנצטרך לאחר מכן:

משולש

ולכן ברגע המתואר באיור:

כאשר נשים לב שגם (רגעית).
נרצה גם למצוא את המהירות הזוויתית של הגלגל. נסמן ב- ו- את נקודת ההשקה של הגלגל עם הרצפה, בהתאמה. כיוון שהגלגול ללא החלקה, מתקיים . לפי משוואות גוף קשיח:

נתון כי רגעית . נשווה ונקבל:

לכן מהירות נקודה (שוב, לפי משוואות גוף קשיח):

ניזהר עם המסקנה הזריזה ש- - היא לא נכונה. שתי הנקודות השונות רוצות לזוז בכיוונים שונים כי הן על גופים קשיחים שונים.
מה שכן ניתן לומר הוא שבכיוון הנורמלי להשקה () הן שוות. את נחלק מ-:

לכן הנורמל , שניצב לוקטור זה, נתון ע”י:

נוסיף ונאמר של- אין עוד רכיב מהירות חוץ מהכיוון הנורמלי הזה. כלומר, אין לו רכיב מהירות בכיוון המשיק, כי הוא גוף קשיח והנקודה לא זזה. לכן מתקיים . נחשב:

לאחר הצבת נתונים נמצא כי:

נשים לב ש- , ולכן:

כעת יש לנו את כל הנתונים לחישוב :

נקבל: