| סטודנט א’ | סטודנט ב’ | |
|---|---|---|
| שם | עידו פנג בנטוב | ניר קרל |
| ת”ז | CLASSIFIED | CLASSIFIED |
| דואר אלקטרוני | CLASSIFIED | CLASSIFIED |
תרגיל 1
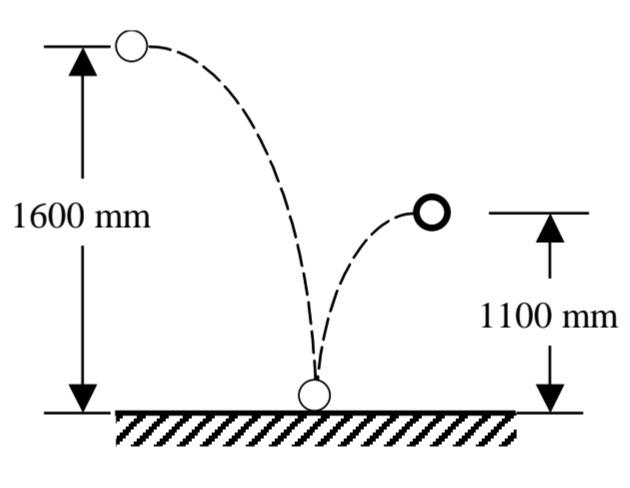
סכמת הבעיה.
סעיף א’
לפני ההתנגשות ואחרי ההתנגשות בקרקע ישנו שימור אנרגיה (רק כוח משמר מבצע עבודה במערכת). לכן, מרגע השחרור עד לרגע לפני ההתנגשות בקרקע:
אנו רוצים שלאחר ההתנגשות הכדור יגיע לגובה שהוא יותר מ-
לפי הגדרת מקדם התקומה של חלקיק:
מאחר ורגע לפני ורגע ההתנגשות, מהירות הכדור היא רק בכיוון האנכי, וגם הנורמל לרצפה הוא בכיוון האנכי:
נציב נתונים ונקבל:
סעיף ב’
מבחינת האנרגיה של הכדור לפני ואחרי ההתנגשות:
לכן, היחס בין אנרגיות אלו:
נציב נתונים ונקבל כי:
כלומר, הפסד האנרגיה המקסימלי של הכדור הוא
תרגיל 2
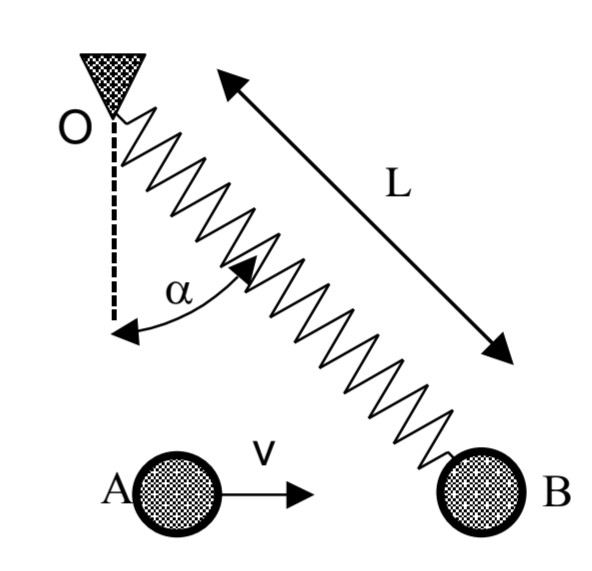
סכמת החלקיקים
הערה:
את הרגע לפני ההתנגשות נסמן ב-
, את הרגע אחרי ההתנגשות נסמן ב- , הרגע שבו המרחק הוא מירבי ב- (כי אז ישנה רק מהירות משיקית), ואת המרחק המקסימלי של מ- ב- .
סעיף א’
נניח ולאחר ההתנגשות יש ל-
נותר לנו למצוא את
מציאת
לפי מקדם תקומה עבור מערכת חלקיקים:
במקרה שלנו,
בנוסף, עד רגע אחרי ההתנגשות, לא פועלים על מערכת החלקיקים כוחות חיצוניים בכיוון
משתי המשוואות (2) ו-(3) נוכל להסיק כי:
מציאת
בכיוון החוצה מהמסך, רגע לאחר ההתנגשות, סך המומנטים על מסה
נציב את הביטויים ל-
סעיף ב’
הביטוי שקיבלנו בסעיף קודם עבור
נציב את הנתון
תרגיל 3
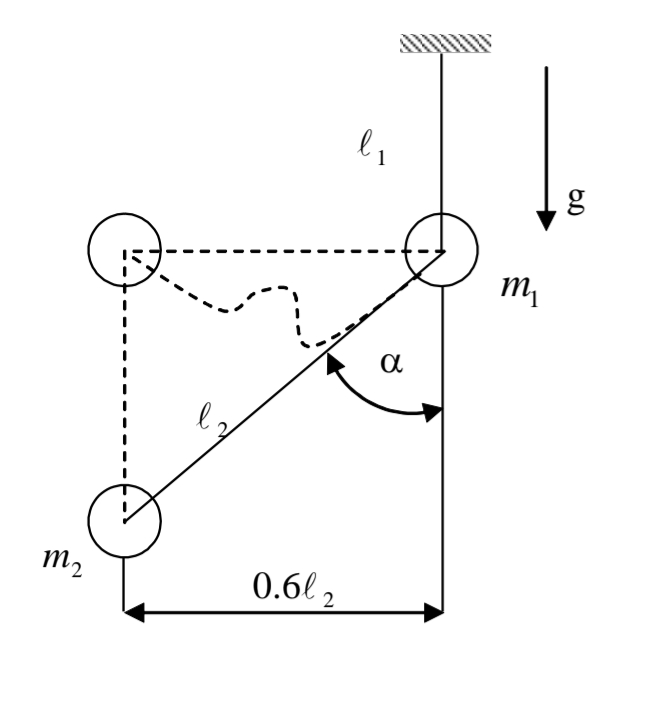
סכמת המסה.
מאזן מתקף על מסה
נבצע מאזן מתקף קווי עבור מסה
נמצא את הכוחות:
דג”ח על מסה
לכן המתקף בפרק זמן ההתנגשות:
הגודל
לפי מאזן מתקף קווי:
נפרק לכיוונים:
אילוץ קינמטי על שני החלקיקים לאחר ההתנגשות:
כיוון ששני החוטים נשארים מתוחים לאחר ההתנגשות, ניתן לומר ש-
מהגדרת הזווית
נציב בתנאי שמצאנו:
מאחר ושני החוטים מתוחים גם לאחר המתקף, המהירות של מסה
מהירות המסה
הכוחות היחידים שמבצעים עבודה מרגע השחרור עד לפני ההתנגשות הם כוחות משמרים (כוח הכבידה), ולכן נוכל להשתמש בשימור אנרגיה. נשים לב שבהתחלה,
נתון כי
מאחר והכדור שוחרר ממנוחה, ופעל עליו כוח רק בכיוון
שימור תנע קווי למערכת:
נשים לב שלא פועלים על המערכת כוחות חיצוניים בכיוון
שילוב המשוואות:
נציב את (3) ב-(1):
נחלק את שתי המשוואות אחת בשנייה:
נציב את (2):
נציב את (4):
נציב בחזרה ב-(4) כדי למצוא את
נציב הכל ב-(2):
נסכם:
הגדלים בכיוון
תרגיל 4
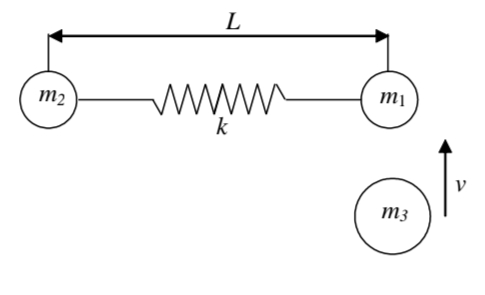
סכמת שלושת החלקיקים.
סעיף א’
הגדרת מערכת הצירים.
שימור תנע קווי:
נשים לב כי לא פועלים על מערכת החלקיקים כוחות חיצוניים בכיוונים
מקדם תקומה
לפי הגדרת מקדם תקומה:
מהנתונים,
נציב את (1):
נציב ב-(2):
נניח ש-
גוף
סעיף ב’
נגדיר מערכת צירים סובבת
מערכת צירים סובבת, כך ש-
מוגדר בכיוון .
נרצה למצוא את
לאחר ההתנגשות, נוכל לומר שלמערכת החלקיקים שכוללת את
כלומר, התנע הזוויתי לאחר ההתנגשות (כאשר המרחק בין המסות הוא
כיוון ש-
לאחר גזירה לפי כלל האופרטור:
נשים לב שלאחר ההתנגשות, התנע הזוויתי של מערכת
נציב הכל בשימור תנע זוויתי:
סעיף ג’
מיד לאחר ההתנגשות, הכוחות היחידים שמבצעים עבודה הם כוחות משמרים (כוח הקפיץ). לכן נוכל לבצע שימור אנרגיה במערכת החלקיקים
מבחינת אנרגיה אלסטית, במקרה הכללי:
ולכן בהתחלה,
מבחינת אנרגיה קינטית, היא בכללי נתונה ע”י:
לאחר ההתנגשות, אין כוחות חיצוניים הפועלים על המערכת, כך שמתקיים שימור תנע קווי:
כאשר
נציב בחזרה בשימור תנע קווי:
או, אם אנחנו עצלנים כמו בפתרון הרשמי:
נציב בחזרה בביטוי לאנרגיה הקינטית הכללית:
רגע לאחר ההתנגשות, רק ל-
נציב הכל בשימור אנרגיה:
תרגיל 5
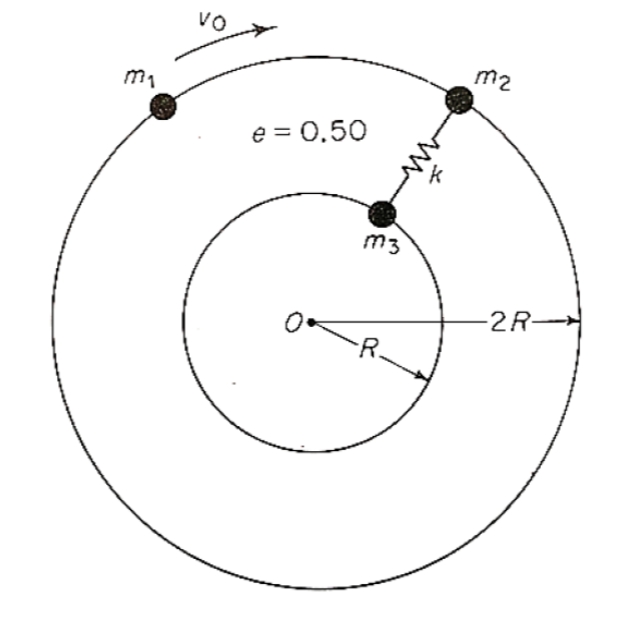
סכמת החלקיקים.
סעיף א’
הגדרת מערכת צירים.
שימור תנע זוויתי:
על מערכת החלקיקים
מהנתונים:
נניח ש-
נציב הכל בשימור תנע זוויתי יחסי:
מקדם תקומה
לפי הגדרת מקדם התקומה:
הכיוון הנורמלי להתנגשות החלקיקים הוא
ולכן גודל המהירויות:
נציב את הנתון
סעיף ב’
שימור אנרגיה:
מרגע לאחר ההתנגשות, הכוחות היחידים שמבצעים עבודה הם כוחות משמרים (כוח הקפיץ), ולכן נוכל להשתמש בשימור אנרגיה במערכת
כאשר
מבחינת אנרגיה אלסטית, במקרה הכללי:
ולכן בהתחלה,
מבחינת אנרגיה קינטית, היא בכללי נתונה ע”י:
ברגע ההתחלה לעומת זאת:
נציב הכל בשימור אנרגיה:
מאחר ו-
ולכן:
שימור תנע זוויתי:
בדומה לסעיף קודם, לאחר ההתנגשות ישנו שימור תנע זוויתי סביב
במקרה הכללי:
ובהתחלה אנו יודעים ש:
נציב בשימור תנע זוויתי:
נציב בחזרה בשימור אנרגיה:
נגזור בזמן:
המהירות
- אם
- אם
נסיק כי גודל המהירות המקסימלית הוא:
סעיף ג’
נחזור לנגזרת של משוואת האנרגיה בזמן:
הפעם, נדרוש
אם
נציב בחזרה בשימור אנרגיה:
