DYN1_005 קינטיקה של חלקיק

→ קודם: DYN1_004הבא: DYN1_006 ←

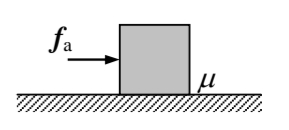
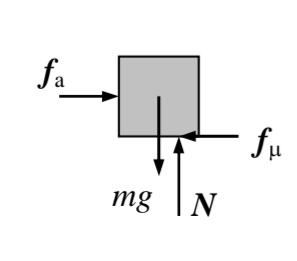
סימונים והגדרות

נעבור על חוקי ניוטון:
חוק ניוטון הראשון: חלקיק הנע במהירות קבועה, שקול הכוחות הפועלים עליו הוא אפס.

חוק ניוטון השני:
עבור חלקיק נע, שקול הכוחות מקיים

כאשר היא מסת החלקיק, ובמסגרת קורס זה נניח שהוא קבוע. בנוסף, נוכל להגדיר את התנע:

ואז את חוק שני נוכל לרשום בצורה השקולה של מאזן תנע קווי:

חוק ניוטון השלישי:
שני חלקיקים מפעילים זה על זה כוחות שווים ומנוגדים .

תנע קווי של חלקיק

נעסוק בעיקר בבעיות של חוק שני, כאשר נשים לב שזוהי משוואה דיפרנציאלית:

ניתן לסווג את הבעיות בדינמיקה לשלושה:

1. תנועת החלקיק נתונה , דרוש למצוא את שקול הכוחות . נקרא גם “דינמיקה הפוכה”.
2. נתונים הכוחות, ודרוש למצוא את התנועה . הכוחות נתונים כפונקציה של מיקום, מהירות וזמן: נדרש לפתור מד”ר מסדר שני עבור , תחת תנאי התחלה .
3. מקרה מעורב - בכיוונים מסוימים נתונים כוחות ויש למצוא את התנועה, ובכיוונים אחרים נתונה תנועה (מאולצת) ונדרש למצוא כוחות. למשל, חלקיק על מסילה, או תנועת מטוטלת.

דוגמה: מקרה א'

חלקיק על דסקה סובבת נע רדיאלית בקצב קבוע. אם נעבוד בקואורדינטות פולאריות:

כיוון שהדסקה סובבת בקצב קבוע:

נדרש למצוא את הכוח הפועל על החלקיק , ולבטאו במערכת הצירים הפולארית .
פתרון:
נבטא את במערכת הפולארית. לפי תאוצה בקואורדינטות פולאריות:

נשים לב כי:

נקבל:

דוגמה: מקרה ב'

אחד לאחד הדוגמה במערכות לינאריות.

דוגמה: מקרה ג'

נתון חלקיק על מישור משופע עם חיכוך קולון (Coulomb).
נדרש למצוא את עבור תנאי התחלה .
וקטור המיקום יהיה:

לכן התאוצה:

נוכל לשרטט דג”ח:

לכן שקול הכוחות:

לפי חוק חיכוך קולון:

במקרה שלנו:

לפי חוק שני:

נציב הכל בשקול כוחות:

מהשוואת מקדמים:

נציב את המשוואה השנייה בראשונה ונקבל מד”ר:

נציב את תנאי ההתחלה:

כאשר .

• עבור (כלומר, ), החלקיק יאיץ במורד השיפוע “לנצח”.
• עבור (כלומר, ), נקבל שהחלקיק יאט עד לעצירה ב- ו- כלשהם.

דוגמה: חלקיק על מסילה מעגלית בשדה כבידה

בדומה לתנועה הרמונית בפיזיקה.

נניח שהחלקיק נע על מסילה חסרת חיכוך. וקטור המיקום בקואורדינטות פולריות:

כאשר במקרה שלנו .
וקטור התאוצה בקואורדינטות אלה:

במקרה שלנו:

דג”ח:

שקול הכוחות:

מחוק שני:

השוואת רכיבים:

בביטוי הראשון קיבלנו ביטוי לכוח הנורמלי. בביטוי השני קיבלנו מד”ר סדר שני ב-, לא לינארי. נכפול את המשוואה ב- ונחלק ב-:

וזוהי משוואת המטוטלת. בהנחת זוויות קטנות, , ואז המד”ר הופכת להיות יותר פשוטה:

שבעלת צורה מאוד דומה למשוואת קפיץ:

פתרון המשוואה יהיה בתצורה של תנודות:

כאשר נקבעים ע”י ת”ה .
נוכל גם לקרב את הפתרון סביב . בקירוב הזווית הזאת:

ונקבל שהמד”ר הופכת להיות:

נקבל את הפתרון:

עבודה מכנית של כוחות הפועלים על חלקיק

עבודה, הספק ואנרגיה קינטית מכנית

העבודה המכנית שהכח מבצע על חלקיק לאורך מסלול מוגדרת לפי:

עבור מסלול תנועה , נוכל:

את האינטגרנד נהוג להגדיר כהספק:

ולכן גם אפשר לרשום:

אם נציב לתוך הגדרת את משוואת התנועה :

את הביטוי בתוך הסוגריים נהוג להגדיר כאנרגיה קינטית:

כך שקיבלנו:

והקשר בין עבודה ואנרגיה:

כלומר:

עבודה מכנית, אנרגיה פוטנציאלית, ואנרגיה כוללת של כוח משמר

כוח נקרא כוח משמר אם העבודה שלו לאורך כל מסלול תנועה סגור הינה אפס:

אם נפרק את המסלול הסגור לשני מקטעים :

נחזיק את קבוע, ונשנה את מקטע מ- ל- כלשהו. עדיין נקבל:

לכן לכל מקטע מסלול שנבחר מ- אל , עבודה הכוח לאורך המסלול תהיה שווה, לא תלויה במסלול אלא רק בבחירת נקודת הקצה של .

תנאים מתמטיים לכך שהכוח הוא משמר:

1. הכוח תלוי במיקום בלבד , כלומר - שדה כוחות.
2. הרוטור של שדה הכוח מתאפס (משפט סטוקס) - .

עבור שדה כוח משמר , שדה משמר פונקציה סקלרית , הנקראת אנרגיה פוטנציאלית, כך שמתקיים:

הערות:

1. זה הפוך מחדו”א 2 מבחינת סימן - נטו הבדלי סמנטיקה בין מתמטיקאים לפיזיקאים).
2. מכך מתקיימים הקשרים של אנרגיה גרביטציונית פוטנציאלית, אנרגיה פוטנציאלית חשמלית, פוטנציאל חשמלי.

כעת את ההספק ניתן לבטא באופן הבא:

לכן, עבור כוח משמר, ההספק:

והעבודה:

כך ש:

כאשר מדגיש את ההנחה שמדובר בכוח משמר.

מצד שני, ראינו ש:

אבל גם , ולכן:

נבצע אינטגרציה ונקבל שעבור כוח משמר:

לביטוי אנו קוראים אנרגיה מכנית כוללת, ומסמנים ב-:

קיבלנו שבמקרה של כוח משמר, לא משתנה - כלומר אין איבוד אנרגיה. נראה בהמשך שעבור כוח לא משמר, כן נתון לשינוי.

דוגמה: שדה קבוע

במקרה של שדה קבוע:

קל לראות כי:

נמצא את פונקציה האנרגיה הפוטנציאלית מתוך אינטגרציה:

מכאן ש:

ולכן הפתרון הכללי:

כאשר הוא קבוע והוא שווה לערך הפוטנציאל כאשר .

דוגמה: כוח מרכזי בעל גודל קבוע

כוח מרכזי הוא כוח שפועל בין שני גופים , בכיוונם. כלומר, . אם , נקבל כי האנרגיה הפוטנציאלית:

כאשר הוא המרחק בין ל-, כלומר .
לכן:

כיוון שכדי להשתמש בנוסחה זו צריך לדאוג שגם וגם מוגדרים בכיוון , ולא בטעות שאחד מהם מוגדר לפי , ניתן להשתמש בנוסחה הבאה כדי למנוע בלבול:

כאשר הינו השינוי באורך הקו בין שתי הנקודות .

דוגמה: קפיץ לינארי

הכוח שקפיץ אלסטי צירי מפעיל הוא פונקציה של התארכותו

כאשר הוא אורך הקפיץ, הוא אורך הקפיץ החופשי, הוא כוח המתיחה בקפיץ, ו-. זהו כוח מרכזי התלוי במקום בלבד ולכן הוא כוח משמר. הפוטנציאל האלסטי של הקפיץ הינו

בקפיץ לינארי היא פונקציה לינארית של המרחק - , כאשר הוא קבוע הקפיץ. נקבל:

דוגמה: כוחות לא משמרים

כוח חיכוך פועל על חלקיק והוא מוגדר ע”י:

כאשר הוא כוח חיצוני אופקי הפועל על הגוף, ו- הוא מהירותו.

מאחר וכוח החיכוך אינו פונקציה של המקום, הוא לא יכל להיות כח משמר. ניתן לראות זאת גם מבחינת ההספק המכני שמבצע הכוח על החלקיק:

לכן, בכל תהליך מחזורי עבודת כח החיכוך תהיה שלילית.

עבודה ואנרגיה של חלקיק

נסווג את הכוחות השונים הפועלים על חלקיק שסכומם הוא הכוח השקול :

כאשר הם כוחות משמרים, ו- הם כוחות לא משמרים. לכן:

העבודה שמבצע הכוח השקול הפועל על חלקיק גורמת לשינוי האנרגיה הקינטית שלו:

העבודה שמבצע כוח משמר על חלקיק שווה למינוס השינוי באנרגיה הפוטנציאלית של החלקיק:

נציב ונקבל:

ולמשוואה זו אנו קוראים מאזן האנרגיה.
סימנו בעבר . לכן נשים לב כי:

נוכל לגזור כדי לקבל את מאזן ההספקים הכללי:

תנע זוויתי של חלקיק

תנע זוויתי מוחלט

הגדרנו בסימונים והגדרות את התנע הקווי:

הגדרה: תנע זוויתי (תנ"ז) המוחלט של החלקיק ביחס לנקודה נייחת נגדיר ע"י:

ה

נגזרת בזמן של תנ”ז:

את הגודל אנו מגדירים כמומנט, ונסמן אותו גם ביחס לנקודה ע”י .
נציב בנגזרת של התנ”ז ונקבל:

למשוואה זו קוראים מאזן תנע זוויתי (מוחלט).

דוגמה: מטוטלת בעלת מוט עם אורך משתנה

נתון כי בציר המטוטלת פועל מנוע המפעיל מומנט טהור על המטוטלת.
וקטורי מיקום ומהירות של החלקיק בקצה:

נסיק כי וקטור התנ”ז:

נגזור בזמן:

מהצד השני של מאזן התנע הזוויתי, נחשב את המומנט (ביחס ל-).

שקול מומנטים (כאשר לא נשכח את המומנט הטהור שמפעיל המנוע, ):

לפי מאזן התנע הזוויתי:

• עבור אורך קבוע , נקבל:

  כאשר הביטוי הוא למעשה מומנט אינרציה של המערכת.

  • עבור המקרה הפרטי בו המטוטלת אופקית (על משטח מקביל לקרקע) וחופשית עם אורך משתנה, מתקיים . נקבל:

  נשים לב שזהו פשוט:

  ולכן:

  כלומר, מתקיים כאן שימור תנע זוויתי. נציב את שמצאנו:

  לכן, עבור תנאי התחלה ו-, נסיק כי:

  שזוהי המשוואה המתארת את גידי (מפיזיקה) מסתובב על כסא עם משקולות בזרועות פרושות לעומת זרועות מכווצות).

דוגמה: מטוטלת על ציר מסתובב

נתון כי .
וקטור המהירות הזוויתית של מערכת :

נרצה למצוא את תנועת המערכת. נעשה זאת בעזרת מאזן תנע זוויתי.
וקטור המיקום:

נגזור לפי כלל האופרטור:

נקבל (לאחר טבלה):

תנ”ז על החלקיק:

נגזור, שוב לפי כלל האופרטור:

נמצא כעת את המומנט.

שקול כוחות:

לכן המומנט:

נוכל כעת להציב במאזן תנ”ז:

רכיב ייתן את משוואת התנועה:

• עבור חוזרים למשטפחת מטוטולת מישורית:

נחשב מצבי שיווי משקל . נציב :

פתרונות של הם .
פתרונות של הם . נשים לב שפתרונות אלו קיימים רק כאשר .
נסתכל על הזזות קטנות מהמצב שיווי משקל התחתון .

המשוואה המקורבת בסביבות :

• עבור נקבל , ואז הוא שיווי משקל יציב.
• עבור , נקבל , ואז הוא שיווי משקל לא יציב.

תנע זוויתי יחסי

הגדרה:

התנ”ז של נקודה ביחס ל- מוגדר כ:

• אם היא נקודה נייחת: כלומר, קיבלנו פשוט את הגדרת התנע זוויתי של חלקיק.

חלקיק הנע ביחס למערכת צירים קבועה שראשיתה ב-. פועל ב- מומנט טהור . נקודה נעה במרחב.

נבדוק איך הגדרה זו משפיעה על מאזן התנע הזוויתי. נשים לב כי:

נגזור:

אנו יודעים ש- וגם , ולכן:

נוכל להמשיך לפתח את למקרה הכללי של:

כאשר הוא מומנט טהור כללי שיכול אולי לפעול על . נציב:

נשים לב ש- הוא פשוט סכום המומנטים על . קיבלנו את מאזן התנע הזוויתי היחסי:

דוגמה: מטוטלת הפוכה על בסיס נע אופקית

דרוש לכתוב משוואת תנועה עבור . נוכל לעשות זאת ע”י מאזן כוחות (מאזן תנע קווי), אבל אנחנו נעשה זאת ע”י מאזן תנע זוויתי יחסי לנקודה .
נמצא את התנע הזוויתי היחסי .

נמצא את ע”י כלל האופרטור, כאשר נשים לב ש- . לאחר טבלה נמצא כי:

נציב בחזרה בביטוי ל-:

נגזור שוב לפי כלל האופרטור, ונקבל:

נמצא את סך המומנטים על
דג”ח:

נותר לנו למצוא את :

נוכל להציב הכל במאזן התנע הזוויתי היחסי. בכיוון נקבל:

בדיקת שפיות זריזה מראה שכאשר , נקבל משוואת מטוטלת (בסימן חיובי כי המטוטלת הפוכה):

העשרה: Kapitza Pendulum

מתקף והתנגשות

מתקף קווי של חלקיק

ניקח את מאזן התנע ה ונבצע עליו אינטגרל:

ל- אנו קוראים מתקף קווי, ולמשוואה שקיבלנו אנו קוראים מאזן מתקף קווי.

ציטוט מיזהר ביידיש:

“השינוי בשוונג שווה לזבאנג”

בהתנגשויות לעיתים מניחים מקדם תקומה (coefficient of restitution):

כדור המתנגש ברצפה, רגע לפני ההתנגשות ורגע אחרי. מקדם התקומה מתאר את היחס בין מהירויות אלה, בכיוון הנורמלי למשטח.

• כאשר , מתקיים , כלומר המהירות של הגוף אחרי ההתנגשות אפסית (bean bag).
• כאשר , מתקיים , כלומר המהירות של הגוף אחרי ההתנגשות שווה למהירותו לפני ההתנגשות (super duper bouncy ball).

דוגמה: כדור קופץ

נתון כדור המשוחרר מגובה . לכן:

בזמן תעופה באוויר, לפי מאזן תנע קווי:

נמשיך עם אינטגרציה:

נמצא את זמן ההתנגשות :

המהירות רגע לפני ההתנגשות:

בהנחת מקדם תקומה :

לכן הגובה לכל :

המקדם תקומה היותר כללי עבור התנגשות עם משטח נע מוגדר ע”י:

כדור נופל על משטח הנע אנכית

נשים לב שמשוואה זו לא נותנת שום מידע בכיוון המשיקי, כלומר על . הנחה אפשרית היא שההתנגשות היא חסרת חיכוך, כך ש- , ולכן גם המתקף בכיוון המשיקי מתאפס:

כך שנקבל למעשה:

מתקף זוויתי של חלקיק

באותו אופן כמו מתקף קווי, נוכל לבצע אינטגרציה על המאזן תנע זוויתי של חלקיק:

נקבל את מאזן המתקף הזוויתי:

ציטוט מיזהר ביידיש:

“השינוי בשווינג שווה לזבוינג”

תרגילים

חלקיק בעל מסה נדחף ע”י מוט מחורץ הסובב במהירות זוויתית קבועה . החלקיק נצמד ע”י קפיץ בעל קבוע אל משטח חלק וחסר חיכוך, בעל צורה דמוית קרדיואידה הנתון בקואורדינטות קוטביות על ידי העקום , כאשר קבוע נתון המהווה את המצב הרפוי של הקפיץ, כלומר הקפיץ רפוי כאשר .

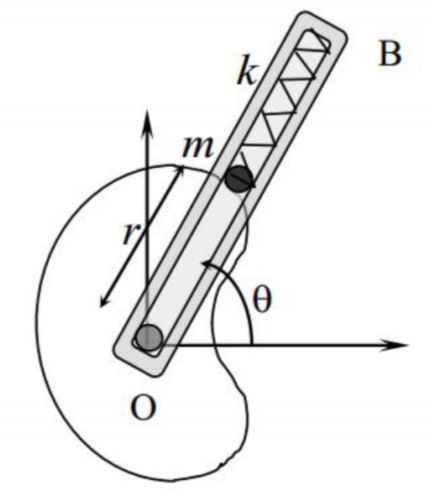
סכימת הקרדיואידה

סעיף א’

מהו כוח המגע הנורמלי בין החלקיק לבין המשטח?

פתרון:
נשתמש במאזן תנע קווי:

נרצה למצוא את התאוצה. וקטור המיקום של :

בקואורדינטות פולאריות:

אנו יודעים ש- . נציב ונקבל:

בהמשך נצטרך גם את :

נרצה כעת למצוא את .

דג”ח על החלקיק. הקפיץ מפעיל את הכוח ; המוט מפעילה כוח ניצב למוט ; והמשטח מפעיל כוח המשורטט בכיוון כללי.

• כוח הקפיץ:

  נמצא את מנתוני השאלה. נסמן את אורך ע”י .

  ולכן כוח הקפיץ:

• כוח נורמלי ממסילה :

• כוח נורמלי מהמשטח:

  נשים לב ש- הוא נורמל למשטח - . אנו יודעים גם ש- . לכן:

  כיוון שהבעיה מישורית, אנו יודעים ש- . נחשב:

  ולכן:

  נציב הכל במאזן התנע הקווי:

  נשים לב שיש לנו כאן שתי משוואות - בכיוון וכיוון .
  בכיוון :

סעיף ב’

מהי המהירות הזוויתית המינימלית בה יתנתק החלקיק מהמשטח?

פתרון:
נדרוש ש- :

אנו רוצים מינימלי, ולכן נגזור את הביטוי. אנו נקבל ש:

נציב בחזרה בביטוי עבור ונקבל ש:

שאלה 2

נתונה המערכת הבאה במצב מנוחה:

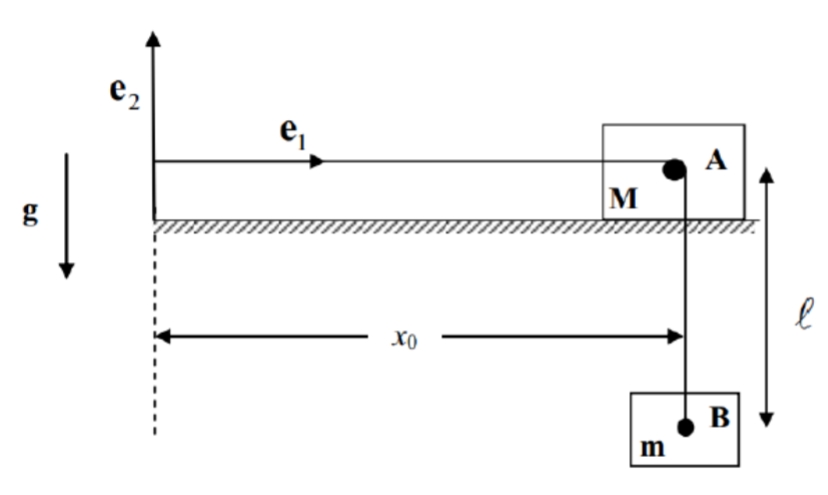
סכימת המשטח

בין המשטח האופקי לגוף קיים חיכוך . כאשר משחררים את המערכת, מתחילה תנועה של הגופים. האורך הכולל של הכבל הינו .
נתון: .
תנאי התחלה:

סעיף א’

כיצד תיראה תנועה של מסה ?

פתרון:
נשים לב שהתנועה של ו- לא כל כך פשוטה כמו שזה נראה.

דג”ח על מסות , ברגע התחלת תנועתן

כפי שניתן לראות מהדג”ח, ל- תהיה תנועה בכיוון האופקי, ואילו ל- תהיה תנועה בכיוון האנכי בלבד. לפיכך, מסה לא תמיד תהיה באותה קואורדינטה אופקית כמו , מה שיוביל לתנועה של מטוטלת שאורך החוט שלה משתנה, וגם ציר הסיבוב שלה זז.

סעיף ב’

דג”ח לאחר תנועה התחלתית

ממאזן תנע קווי:

המיקומים של החלקיקים:

לכן התאוצות:

הכוחות (מהדג”ח):

נמצא משוואה נוספת מאילוצים קינמטיים. נשים לב שאורך החוט תמיד קבוע - .

אילוץ קינמטי

מחיבור וקטורים נקבל את המשוואה הוקטורית:

ממכפלה סקלרית (השוואת גדלים):

נרצה משוואה בנעלמים , נגזור את המשוואה פעמיים:

נציב את תנאי ההתחלה (). נקבל:

נציב הכל במאזן תנע הקווי עבור כל גוף ונקבל בסוף:

נציב בביטוי של המתיחות ונקבל:

סעיף ג’

מה צריכה להיות המסה המינימלית של לקיום התנועה?

פתרון:
כדי שתהיה תנועה, צריך שלמסה תהיה בתחילת התנועה תאוצה בכיוון השלילי של , ולכן צריך לדרוש ש- . כלומר, סכום הכוחות על מסה צריך להיות שונה מ-.
נציב ונקבל:

שאלה 3

קוביה בעלת מסה חופשית לנוע על מוביל אנכי חסר חיכוך. אל הקוביה מחוברים קפיץ שאורכו ההתחלתי מתואר ע”י וחוט שאורכו ההתחלתי מהמסה לגלגת מתואר ע”י הנמשך בכוח קבוע , כמו כן גובה המסה מהקרקע מתואר ע”י כמתואר באיור:

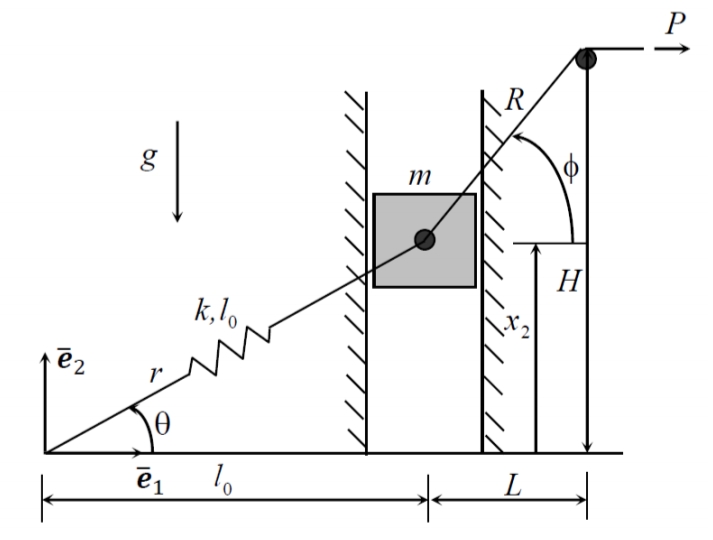
סכימת המערכת

נתונים הגדלים הכוח הקבוע; המרחק האופקי בין ראשית הצירים לבין המסה במוביל האנכי; הוא הגובה האנכי בו הכוח הקבוע מופעל; הוא המרחק האופקי בין המסה מהמוביל האנכי לגלגלת; הוא מסת הקוביה; הוא קבוע הקפיץ;

תנאי ההתחלה הם וגם , כאשר נתון שבתחילת התנועה הקפיץ רפוי, כלומר הינו האורך הרפוי של הקפיץ. המערכת משוחררת ממנוחה.

מהי מהירות המסה כתלות בפרמטרים הידועים ובהעתק ?

פתרון:
נשים לב שביקשו את הנגזרת של הקואורדינטה כתלות בקואורדינטה עצמה. שאלה זו מעידה על כך שנצטרך להשתמש בשיקולי אנרגיה.

לפי מאזן האנרגיה:

נגדיר את וקטור המיקום:

נגזור:

נרצה למצוא את הכוחות.

דג”ח על המסה

הכוחות הלא משמר שפועל הוא . נחשב את העבודות שלו לפי הגדרה:

מבחינת השינוי באנרגיה הקינטית:

נפרק את האנרגיה פוטנציאלית:

נציב תנאי התחלה:

נשים לב גם כי:

נציב הכל במאזן אנרגיה ונקבל:

שאלה 4

חלקיק בעל מסה אשר גובהו מן הקרקע מתואר ע”י הקואורדינטה , נורה במהירות אופקית התחלתית בגובה התחלתי וזווית התחלתית , על גבי משטח קוני בעל זווית חלק כמתואר באיור:

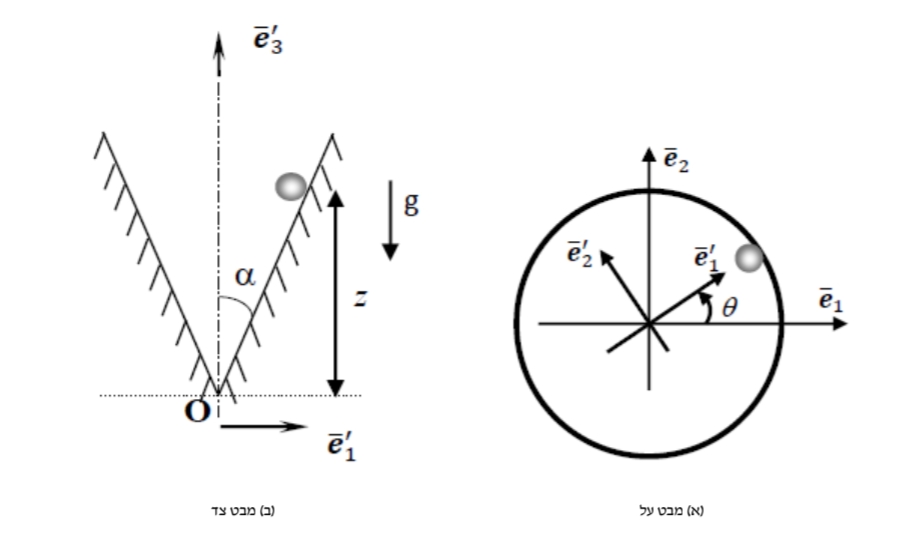
מבט על וצד של החרוט

סעיף א’

מה יהיה הגובה המקסימלי והמינימלי של החלקיק כתלות ב- ו-?

פתרון:
מחפשים גובה מינימלי ומינימלי כתלות במהירות (וגם גובה התחלתי). נסיק שנצטרך שוב לבצע מאזן אנרגיה:

וקטור המיקום של החלקיק:

נגזור לפי כלל האופרטור ונקבל:

אנו יודעים ש- . נציב ונקבל תנאי התחלה:

נמצא את הכוחות.

דג”ח על הכוחות

נחשב את סך העבודה של הכוחות הלא משמרים. במקרה שלנו זהו רק :

עבור השינוי באנרגיה הקינטית:

השינוי באנרגיה הפוטנציאלית:

נציב הכל במאזן אנרגיה ונקבל:

נרצה כעת למצוא ביטוי ל-. נביט במומנט סביב .

כלומר, קיבלנו של- אין רכיב ב- שהוא כיוון קבוע, ולכן ספציפית בכיוון שלו נוכל להשתמש בשימור תנע זוויתי:

נמצא את התנע הזוויתי:

נוכל להשוות בין המצב ההתחלתי למצב הסופי:

נציב בחזרה במאזן אנרגיה:

נרצה למצוא מינימלי ומקסימלי, ולכן נאפס את :

נפתור את המשוואות:

נקבל את הפתרונות הבאים:

הפתרון הוא לא פיזיקלי כי הוא שלילי. נישאר עם:

כאשר מי מהם מינימלי או מקסימלי תלוי בפרמטרים.

סעיף ב’

מה המהירות ההתחלתית בה החלקיק ימשיך לנוע בגובה ?

פתרון:
נישאר בגובה קבוע אם . כלומר נדרוש ש- :

→ קודם: DYN1_004הבא: DYN1_006 ←