DYN1_HW010 תרגיל בית 10

	סטודנט א’	סטודנט ב’
שם	עידו פנג בנטוב	ניר קרל
ת”ז	CLASSIFIED	CLASSIFIED
דואר אלקטרוני	CLASSIFIED	CLASSIFIED

תרגיל 1

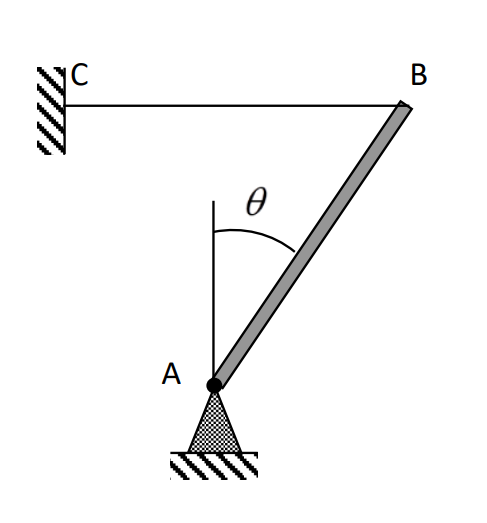
סכימת המוט

סעיף א’

לפי מאזן תנע זוויתי יחסי של גק”ש מישורי:

הנקודה קבועה, לכן תאוצתה אפס:

נמצא את המומנט:

דג”ח על המוט. הכיוון של הריאקציה הוא כללי.

לכן שקול המומנטים סביב :

מבחינת מומנט האינרציה, ראינו כי ביחס לנקודת קצה של מוט, ערכו הוא:

נציב במאזן תנע זוויתי (יחסי):

הזווית מוגדרת חיובית בכיוון השלילי של , כך ש- , ולכן:

סעיף ב’

נפתור את המד”ר שקיבלנו בסעיף קודם. נוכל להכפיל את שני הצדדים ב-:

נשים לב ש- וגם . לכן, כאשר נבצע אינטגרציה לפי לשני הצדדים:

נציב תנאי התחלה :

נציב בחזרה:

סעיף ג’

מהדג”ח על המוט, ניתן למצוא ע”י מאזן תנע קווי ש:

נעביר אגפים:

מרכז המסה של המוט נמצא במרחק מ-:

נגזור פעמיים:

נציב בחזרה בביטוי ל-:

תרגיל 2

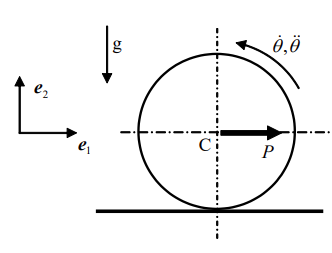
סכימת הגליל

נחשב עבור כללי.

דג”ח על הגליל. אנו מניחים כי הכיוון של הוא שלילי, אבל זו החלטה שרירותית לחלוטין.

התנועה של מרכז המסה תלויה רק ב-, ולכן:

לפי מאזן תנע קווי:

לפי מאזן תנע זוויתי:

בדסקה מישורית - , ולכן:

מ-(1) ניתן לראות כי . נציב:

אם , זה אומר שיש תנועה בין הנקודה למישור - כלומר אנחנו כבר במקסימום שבו יכל להיות. אם , אז נוכל לומר ש- נייח ביחס למישור, מה שאומר שיש אי-החלקה. לכן, נפרק למקרים, כאשר נשים לב שלפי (2), מתקיים :

• אם :
  ישנה אי-החלקה. לכן, , ואז לפי קשרי גוף קשיח: ולכן: כלומר, קיבלנו ש: נוכל לגזור כדי לקבל: נציב ב-(3): נבצע אינטגרציה פעמיים, כאשר נשים לב שתנאי ההתחלה הם : מ-(4) ו-(5) נוכל למצוא את : מאינטגרציה פעמיים ותנאי ההתחלה : אם נציב זאת חזרה ב-(1), נקבל ש- מקיים: ^eq-7a ^eq-6a ^eq-5

כלומר, אם , אז . לפיכך, אם , אז לא מתקיים , ואז כבר יש החלקה. במקרה זה:

• אם :
  ישנה החלקה, ולפי (1) מתקיים: נבצע אינטגרציה פעמיים ונקבל מתנאי התחלה ש: מ-(8) ו-(3): מאינטגרציה פעמיים והתחשבות בתנאי התחלה: ^eq-10a ^eq-9a

נוכל כעת להתייחס לכל אחד מהסעיפים:

סעיף א’

אם , אז כך שמתקיימת אי-החלקה. לכן, נציב ב- ו-:

סעיף ב’

אם , אז גם כך שמתקיימת אי-החלקה. לכן, נציב ב- ו-:

סעיף ג’

אם , אז , כך שמתקיימת החלקה. לכן, נציב ב- ו-:

תרגיל 3

דג”ח על הכדור באולינג. אנו מניחים כי הכיוון של הוא שלילי, אבל זו החלטה שרירותית לחלוטין.

התנועה של מרכז המסה תלויה רק ב-, ולכן:

לפי מאזן תנע קווי:

נשים לב שזהו תרגיל מאוד דומה לתרגיל קודם, רק הפעם אין כוח , ומומנט האינרציה (או יותר נכון, טנזור האינרציה) הוא מרחבי:

מאחר והתנועה של הכדור היא חד ממדית (נניח ב-), וטנזור האינרציה איזוטרופי, המשוואות אויילר שלנו הן פשוט משוואה אחת בכיוון :

שזהו מקרה זהה לשאלה הקודמת, רק הפעם שונה:

כיוון שיש החלקה בהתחלה, , ואז לפי (2), . נציב:

לכן המהירות הזוויתית (בהתחשבות בתנאי התחלה):

מ-(1) אנו יודעים ש- . נציב ב-(3):

נציב את (4):

לכן, מאינטגרציה פעמיים והתחשבות בתנאי התחלה:

מתרגיל קודם, כאשר מתקיימת אי-החלקה, מתקיים . נמצא את רגע זה (נציב את (6) ו-(5)):

נציב ב-(7):

תרגיל 4

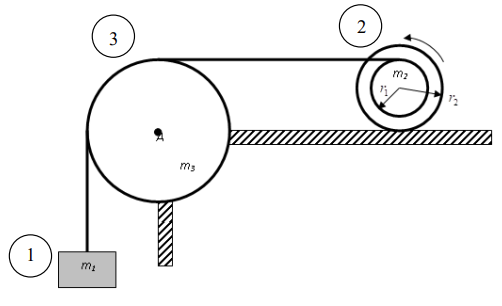
סכימת המשקולות

סעיף א’

מסה :

דג”ח על

ממאזן תנע קווי:

נרצה למצוא את .
מסה :

דג”ח על מסה . כיוון הריאקציה נבחר באופן שרירותי.

ממאזן תנע זוויתי יחסי למרכז המסה של :

נתון כי אין החלקה בין הכבל לבין הגלגלת , כך שהמהירות של נקודה על הגלגלת שווה למהירות הכבל שנסמן :

ממשוואות גוף קשיח:

ולכן:

נציב ב-(2) (כאשר נסמן ):

מסה :

דג”ח על מסה . כיוון הכוח נבחר באופן שרירותי.

ממאזן תנע קווי (כאשר ):

בהנחה ובאמת מסה מתגלגלת ללא החלקה, אין תנועה בין הנקודה על המסה והנקודה על המישור, כך ש- .
נמצא עוד משוואה ממאזן תנע זוויתי יחסי למרכז המסה של :

ממשוואות גוף קשיח:

נסמן , כך ש:

נגזור:

נציב בחזרה במאזן תנע זוויתי יחסי:

נציב ב-(4):

נרצה כעת לקשר בין (תאוצת מרכז המסה ) ל- (תאוצת הכבל). נשים שהרכיב האופקי של תאוצת היא למעשה , ונוכל לקשר אותה ל-. ממשוואות גוף קשיח:

התאוצה:

ולכן:

נציב את הביטוי שמצאנו ל-:

שילוב המשוואות:

נציב את שמצאנו ב-(5):

נבודד את :

נציב ב-(3):

נציב ב-(1):

תאוצת הכבל היא פשוט תאוצת המסה , ולכן:

סעיף ב’

נציב נתונים ב-:

בסעיף קודם מצאנו כי:

נציב את הביטויים שמצאנו ל- ו-:

נציב את הביטויים הנתונים ואת (6) (נזכור כי ):

מאחר ו- , נסיק כי , כך שלמעשה ישנה החלקה בין המסה למישור.

סעיף ג’

הפעם, כיוון שיש החלקה, אנו יודעים כי , אבל אנחנו לא יכולים להסיק כי . המשוואות שכן נכונות מסעיף קודם הן:

וגם כמובן .
נציב את תנאי ההחלקה ב-(7):

נציב ב-(8):

נציב את ואת שמצאנו ב-(4):

נציב נתונים כי זה כבר נהיה מסובך:

נציב ב-(3) עם נתונים:

נציב ב-(1):

נציב את :

הערות:

1. בדוק יש פה איפשהו טעות.
2. נודר נדר צריך לעדכן את הגליונות הישנים האלה.