DYN1_007 קינטיקה של גוף קשיח

→ קודם: DYN1_006הבא: DYN1_008 ←

מבוא

אנו יודעים שגוף קשיח הוא רצף של אלמנטי מסה ששומר על צורה קבועה.

הגדרת אלמנט המסה

נקביל את הגוף ממערכת חלקיקים, לאלמנט מסה בגק”ש. כל אלמנט מסה מוגדר במיקום עם מהירות (או ).

תנע קווי של גק”ש

תנע קווי

במערכת חלקיקים, הגדרנו את סך התנע של המערכת בצורה
במקרה של גוף קשיח, נגדיר אותו בצורה מאוד דומה:

עבור מרכז המסה, נגדיר:

אם הצפיפות אחידה, נוכל לבצע אינטגרל על הנפח במקום על המסה:

ואז מרכז המסה הוא פשוט תכונה גאומטרית.
מבחינת מהירות מרכז המסה:

ולכן מתקבל כי התנע הקווי הינו:

כוחות על גוף קשיח

במערכת חלקיקים, חילקנו את הכוחות לכוחות פנימיים וכוחות חיצוניים. בגוף קשיח, נוכל להתעלם מהכוחות הפנימיים, מסיבה שראינו כבר במערכת חלקיקים, כאשר החלקיקים נשארים במקום קבוע אחד ביחס לשני (הם לא משפיעים על ההספק או העבודה).

מבחינת הכוחות החיצוניים, נוכל לפרק אותם לכוחות נקודתיים הפועלים בנקודות , ולכוחות מפולגים על פני שטח או מסה. את הכוחות המפולגים ניתן לפרק עוד יותר לכוחות גוף כמו כבידה, ולכוחות שפה כמו לחץ או כוחות גזירה הפועלים על השפה.

סכום הכוחות החיצוניים על גוף קשיח:

במקרה של כבידה, פילוג הכוח אחיד - , ולכן:

הערה:

בקורס זה פחות נתייחס לתרומת כוחות שפה מפולגים - מתייחסים אליהם יותר בזורמים.

מאזן תנע קווי

עבור מאזן תנע קווי של מערכת חלקיקים, קיבלנו כי הכוחות הפנימיים התבטלו, ואז נשארנו רק עם הכוחות החיצוניים - .
עבור גוף קשיח, באופן דומה, מתקבל מאזן תנע קווי רק עם כוחות חיצוניים:

תנע זוויתי של גק”ש

תנע זוויתי מוחלט

נגדיר תנע זוויתי של גוף קשיח באופן מאוד דומה למערכת חלקיקים:

בנוסף, מומנט כולל הפועל על גוף קשיח, ביחס לנקודה :

כאשר הוא מומנט טהור על הגוף קשיח, - הוא כוח גוף מפורס.
מהכללה של הפיתוח במערכת חלקיקים (שאויילר ביצע, ולא נראה כאן), נקבל מאזן תנ”ז מוחלט לגוף קשיח:

תנע זוויתי יחסי

נגדיר תנ”ז יחסי בגוף קשיח, ביחס לנקודה נעה כללית:

ניתן להוכיח (כמו במערכת חלקיקים) קשר בין תנ”ז יחסי למוחלט:

מקרים פרטיים:

1. אם בוחרים נייחת מקבלים .
2. אם בוחרים במרכז המסה , אז , ולכן נקבל: אם ניקח הפרש בין משוואה (7.1) ל-(7.2), נקבל: ^eq-7-3

מומנט (חיצוני) ביחס לנקודה :

נגזור את (7.3) ונקבל כי הוא שווה לביטוי של - קיבלנו מאזן תנ”ז יחסי של גוף קשיח:

עבור נייחת או במהירות קבועה, מתקיים , ואז . אם במרכז המסה, מתקיים :

שזהו מאזן תנ”ז יחסי למרכז של גוף קשיח. ביחד עם מאזן תנע קווי של גוף קשיח, נקבל 6 משוואות שמתארות את תנועת הגוף הקשיח, שנקראות משוואות ניוטון-אויילר.

מומנט אינרציה של גק”ש מישורי

עבור גוף קשיח, אם בוחרים נקודת ייחוס צמודת-גוף , ניתן להשתמש בקשרי קינמטיקה של גוף קשיח:

אלמנט מסה עם מיקום ומהירות מקיים קשרי גק”ש עם נקודה :

נציב ב-:

נתחיל ממקרה של תנועה מישורית:

לכן:

נציב ב-:

נקרא לאינטגרל זה בשם מיוחד.

הגדרה:

מומנט האינרציה של הגוף ביחס לנקודה מוגדר כ:

זהו למעשה סקלר, והוא תכונה של הגוף ביחס לנקודת גוף .
גודל זה גם אינווריאנטי ביחס לבחירת כיווני .

עבור צפיפות מסה קבועה ליחידת שטח , המומנט אינרציה הופך להיות תכונה גאומטרית:

דוגמה: מוט דק ואחיד

נתון מוט דק ואחיד בעל אורף ומסה , עם צפיפות אחידה אורכית .

נחשב את מומנט האינרציה ביחס לנקודה קצה :

דוגמה: מוט עם מסה בקצה

עבור מוט חסר מסה, עם מסה בקצה שלו:

דוגמה: טבעת דקת דופן

מאחר ובכל נקודה המרחק שווה, מתקיים:

דוגמה: דיסקה אחידה מלאה

במקרה של צפיפות אחידה, מתקיים:

ולכן נוכל לומר כי:

דוגמה: טבעת עבת דופן

נקבל לאחר קצת אלגברה מעצבנת:

משפט שטיינר

• משפט שטיינר במוצקים

נתון , ונרצה למצוא - מומנט אינרציה ביחס לנקודת גוף אחרת.

משפט:

בהינתן מומנט אינרציה ביחס לנקודת מרכז המסה , מומנט האינרציה ביחס לנקודה הוא:

פיתוח:
על פי הגדרה:

נציב :

מאזן תנע זוויתי יחסי של גק”ש מישורי

בתנע זוויתי יחסי, ראינו כי המאזן ביחס לנקודה :

ראינו במומנט אינרציה (במקרה המישורי) ש:

ולכן, נוכל לומר כי:

אנרגיה קינטית בגק”ש מישורי

במערכת חלקיקים:

לכן, בגוף קשיח:

נוכל לבחור נקודת ייחוס צמודת גוף , כך ש- :

במקרה המישורי:

• אם הנקודה היא מרכז המסה, נוכל פשוט לחשב את:
• אם הנקודה היא נקודה נייחת , אז נוכל פשוט לחשב:

תרגילים

שאלה 1

גליל שרדיוסו מחובר באופן קשיח לתוף שרדיוסו . לגליל ולתוף יש מרכז משותף (נקודה ). המסה המשותפת של התוף והגליל היא , מומנט האינרציה המשותף ביחס למרכז המסה הוא . הגליל מונח על מסילה אופקית וקבועה. על התוף כרוך כבל אופקי המתחבר דרך גלגלת חסרת חיכוך וחסרת מסה ב- אל משקולת שמסתה בקצה הכבל . מסת הכבל זניחה. משחררים את המערכת ממנוחה כאשר אף אחד מהמסות לא נעה או מסתובבת כאשר הכבל מתוח (הכבל אינו מחליק על הגליל).

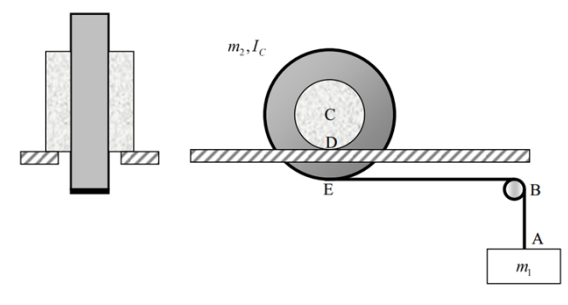
סכימת הגליל

בהנחה שהגליל מחליק על המסילה, מהו החסם העליון של מקדם החיכוך בין המסילה לגליל אשר יבטיח שתהיה החלקה ביניהם בתחילת התנועה?

פתרון:
בהחלקה הכוח שפועל לנו על הגליל הוא חיכוך, והחיכוך תמיד פועל בכיוון הפוך לכיוון התנועה. לכן אנחנו צריכים לוודא שהכוח שפועל על הגליל ברגע הנתון יהיה הפוך מכיוון תאוצתו.

דג”ח על הגליל ועל המשקולת

נעשה שימור תנע קווי על הגליל והתוף:

אנחנו יודעים ש- :

לכן:

משימור תנע קווי על המשקולת (נשים לב ש-):

ממאזן תנע זוויתי יחסי על התוף:

כלומר קיבלנו:

נרצה למצוא את החיכוך:

יש לנו 3 משוואת (1), (2), (3) וארבעה נעלמים .
נשתמש בעובדה שיש לנו כבל קשיח, כלומר יהיה לנו אילוץ קינמטי בין התאוצות של הגליל והמשקולת.

כאשר היא מהירות הנקודה על התוף, ו- היא מהירות הנקודה של הכבל.

מכיוון שהכבל אידאלי (לא נמתח) כל הנקודות עליו זזות במהירות בגודל זהה, לכן:

ממשוואות גוף קשיח נקבל את הקשר בין המהירות בנק’ E למהירות מרכז הגליל C:

מאחר ו-:

כדי למצוא קשר בין הנעלמים שלנו () נגזור לפי הזמן:

נוכל כעת למצוא מארבעת המשוואות ש:

נדרוש שכיוון התנועה וכיוון כוח החיכוך הפוכים: . מבחינת כוח החיכוך, ראינו כי:

נחשב את התאוצה ממשוואות גוף קשיח:

כאשר נכפיל סקלרית את ו- הרכיבים בכיוון ייפלו (כי הכוח הוא בכיוון בלבד). נכפיל ונקבל:

ולכן:

נציב את , ונקבל:

שאלה 2

קפיץ ליניארי בעל קשיחות קבועה ואורך רפוי מחובר בקצה אחד לקיר בנקודה ובקצהו השני (קצה ) מחובר לגליל בעל מסה ורדיוס . כוח הכובד ליחידת מסה פועל בכיוון . מקדם החיכוך בין הגליל והמשטח האופקי מתחתיו הוא . נתון כי מומנט האינרציה של הגליל סביב מרכז המסה שלו הוא . דרוש לפתור עבור הנתונים הבאים:

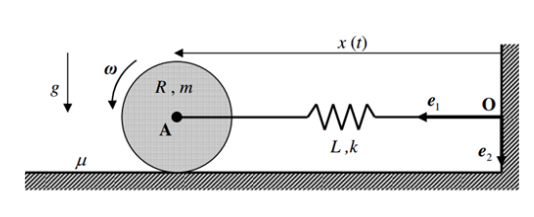
סכימת הגליל

חלק א’

שלושת הסעיפים הבאים מתייחסים לת”ה הבאים:
ברגע ההתחלה הקפיץ נמתח לאורך התחלתי , מרכז המסה של הגליל במנוחה (לא זז) ובו זמנית הגליל מחלקי ומסתובב במהירות זוויתית התחלתית מוחלטת .

סעיף א’

מהו גודל שעבורו תאוצת מרכז המסה מתאפסת?

פתרון:

נשתמש במאזן תנע קווי:

נפרק לכיוונים:

מחוק הוק, . בנוסף, כיוון שיש כבר תנועה, אנחנו יכולים לומר ש- .
נציב חזרה בשימור בכיוון :

ביקשו למצוא את האורך בו . נדרוש זאת:

קיבלנו:

סעיף ב’

עבור מהסעיף הקודם, מהו הזמן שבו הגליל מפסיק להחליק בפעם הראשונה?

פתרון:
ממאזן תנע זוויתי יחסי:

לכן נקבל:

הגליל יפסיק להחליק כאשר .
נעשה אינטגרל כדי למצוא קשר לזמן, ונראה עבור איזה נקבל :

נחלץ את :

סעיף ג’

מהי כמות האנרגיה שמתבזבזת על ידי כוח החיכוך?

פתרון:

נוכל לראות שהכוח היחיד שמבצע עבודה במקרה זה הוא , ולכן:

מבחינת האנרגיה הקינטית בהתחלה ובסוף:

לכן:

חלק ב’

ארבעת הסעיפים הבאים מתייחסים לת”ה הבאים:
מותחים את הקפיץ לאורך של כאשר הגליל במנוחה (לא מסתובב ולא זז). בחלק זה הניחו שהגליל לא יחליק על המשטח האופקי אחרי שחרור המערכת.

סעיף ד’

מהי תאוצת מרכז המסה של הגליל (נקודה ) מיד לאחר שחרור המערכת?

פתרון:
אנחנו יודעים שהמהירות היחסית בנק’ המגע היא :

מכיוון שנק’ היא נק’ על הקרקע, מהירותה ולכן:

לפי משוואות גוף קשיח:

נגזור ונקבל:

ולכן:

דג”ח על הגלגל

הפעם מכיוון שאין החלקה, החיכוך הוא חיכוך סטטי, ואנחנו לא בטוחים לאן החיכוך יפעל. נסמן אותו שרירותית בכיוון שמאל (אם נקבל סימן מינוס החיכוך יהיה לימין).

לפי מאזן תנע קווי:

כדי למצוא את נשתמש במאזן תנע זוויתי שכבר ביצענו בסעיפים קודמים:

נציב את שמצאנו:

נציב בחזרה במאזן תנע קווי (בכיוון ):

ולכן, ברגע ההתחלה:

סעיף ה’

מהו גודל כוח החיכוך שפועל על הגליל מייד אחרי שחרור המערכת?

פתרון:
נציב את התאוצה שמצאנו בכוח החיכוך:

סעיף ו’

ברגע בו מהו גודל המהירות הזוויתית של הגליל?

פתרון:
אם אין החלקה אז כוח החיכוך לא מבצע עבודה, ואין עוד כוחות לא משמרים במערכת שמבצעים עבודה, אז יש שימור אנרגיה:

מבחינת השינוי באנרגיה הקינטית, נזכור שבהתחלה הגוף לא זז. לכן:

מבחינת השינוי באנרגיה הפוטנציאלית:

נציב בשימור אנרגיה ונקבל:

שאלה 3

שתי דסקות אחידות שמסותיהן ורדיוסיהן בהתאמה, קשורות זו לזו באמצעות כבל בעל מסה זניחה, הכרוך עליהן, כאשר בין הכבל לדסקות אין החלקה.

במרכזה של הדסקה עובר ציר שמיקומו קבוע כך שהדסקה מסתובבת סביבו ללא חיכוך. קיים שדה כבידה:

משחררים את הדסקה השנייה והיא נופלת במישור האנכי תוך כדי שחרור הכבל. הקואורדינטה מתארת את מיקומה ביחס למצב ההתחלתי.

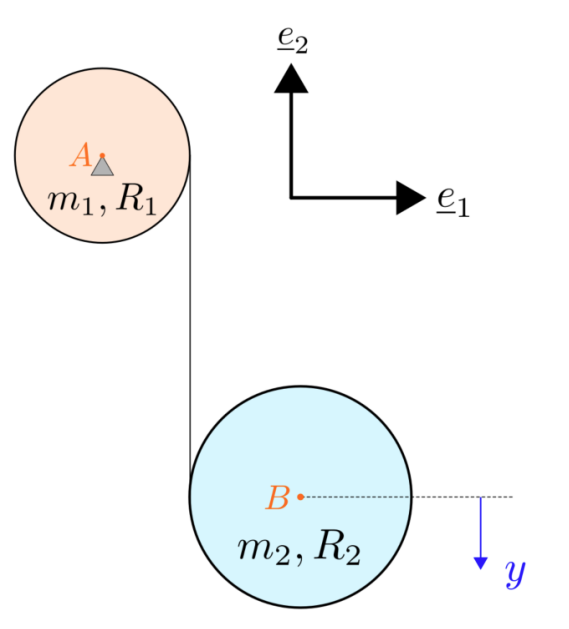
סכימת הדסקות

נתונים: .
מהי התאוצה המוחלטת של מרכז הדסקה ?

פתרון:

דג”ח על הדסקות

מאחר והבעיה מישורית:

נסמן את מיקום המסה ביחס למיקום ההתחלתי שלה ב-:

כך שהמהירות והתאוצה הן:

לפי מאזן תנע קווי על דסקה :

ממאזן תנע זוויתי על דסקה :

ממאזן תנע זוויתי על דסקה :

מומנט אינרציה של דסקה ברדיוס כללי הוא , ולכן במקרה שלנו:

נמצא קשר בין לבין ו-. נוכל להשתמש במשוואות גוף קשיח. על דסקה :

נותר לנו למצוא את . נסמן ב- ו- את הנקודות המתאימות על החוט. נתון שהחוט לא מחליק על הדסקות, כך שמתקיים:

ולכן וגם . מפני שהחוט קשיח, המרחק ביניהן קבוע:

ולכן:

כך ש:

נציב בביטוי ל-:

את נוכל למצוא גם ממשוואות גוף קשיח, הפעם על דסקה :

נציב בביטוי ל-:

→ קודם: DYN1_006הבא: DYN1_008 ←