ELM1_002 הספק פעיל, הגבי ונדמה

מבוא

• יש להיזכר במעגלי זרם משתנה.

המושגים של הספק פעיל, הֶסְפֵּק הֶגֵּבִי והֶסְפֵּק נִדְמֶה ממלאים תפקיד מרכזי בטכנולוגיית אנרגיה חשמלית. למעשה, העברת אנרגיה חשמלית וההתנהגות של מכונות זרם חילופין (AC) לעיתים קרובות קלות יותר להבנה כאשר עובדים עם הספקים, מאשר כאשר מתמודדים עם מתחים וזרמים.
המונחים הספק פעיל, הספק הגבי והספק נדמה חלים על מעגלי זרם חילופין במצב יציב, שבהם המתחים והזרמים הם סינוסואידיים. אין להשתמש בהם לתיאור התנהגות במצב מעבר (transient-state), וגם לא ניתן ליישם אותם על מעגלי זרם ישר (DC).

נתחיל בניתוח של ההספק הרגעי במעגל זרם חילופין. לאחר מכן נגדיר את משמעות ההספק הפעיל וההספק ההגבי, וכיצד ניתן לזהות מקורות וצרכנים. בהמשך נגדיר את ההספק הנדמה ומקדם ההספק. לאחר מכן נראה כיצד ניתן לפתור מעגלי זרם חילופין באמצעות מושגים אלה של הספק. לסיום, נשתמש בכתיב וקטורי כדי לקבוע את ההספק הפעיל וההספק ההגבי במעגל זרם חילופין.

הספק רגעי

ההספק הרגעי המסופק למכשיר הוא פשוט תוצאת כפל של המתח הרגעי על פני הדקים שלו עם הזרם הרגעי הזורם דרכו. הספק רגעי תמיד נמדד ב-, ללא קשר לסוג המעגל שבו נעשה שימוש. ההספק הרגעי יכול להיות חיובי או שלילי. ערך חיובי מצביע על כך שההספק זורם אל תוך המכשיר. לעומת זאת, ערך שלילי מציין שההספק זורם החוצה מהמכשיר.

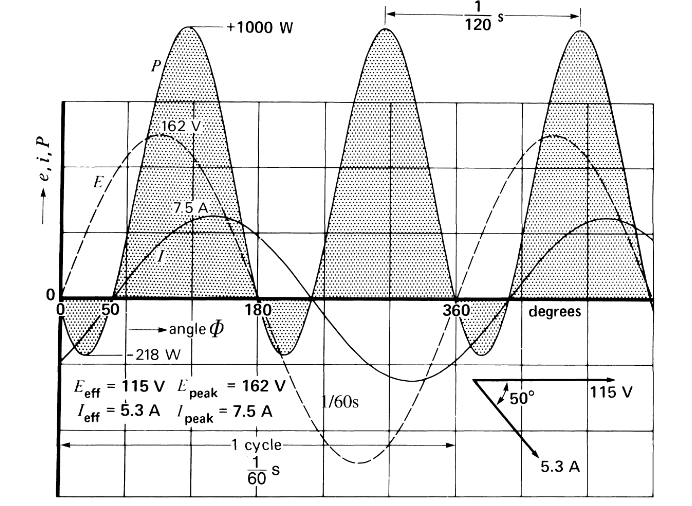
מתח רגעי, זרם רגעי והספק רגעי במעגל AC. מ-(Wildi, 2014).

למרות שזרימת הספק ממכשיר הנחשב כעומס למכשיר הנחשב כמקור עשויה להיראות כבלתי אפשרית, הדבר מתרחש לעיתים קרובות במעגלי זרם חילופין (AC). ההסבר לכך ניתן בסעיפים הבאים. כמו כן, נציין כי השיאים החיוביים בגרף לעיל מתרחשים במרווחים של שניות. משמעות הדבר היא שתדר מחזור ההספק הוא , שזה פי שתיים מתדר המתח והזרם שמייצרים את ההספק. שוב, תופעה זו היא נורמלית לחלוטין: תדר זרימת ההספק בזרם חילופין הוא תמיד כפול מתדר הרשת.

הספק פעיל

המעגל הפשוט של זרם חילופין שמופיע באיור הבא מורכב מנגד שמחובר לגנרטור AC.

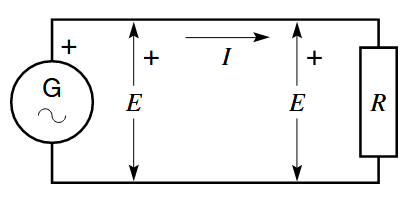
מקור מתח חילופין יוצר זרם חילופין במעגל עם נגד. (Wildi, 2014).

המתח והזרם האפקטיביים מסומנים ב- ו- בהתאמה, וכפי שנצפה במעגל שבו קיים רק נגד, הפאזורים של ו- נמצאים באותו מופע:

פאזורים ו- באותו מופע (in phase). (Wildi, 2014).

אם נחבר מד-הספק (wattmeter) למעגל, נקבל קריאה של הספק ב-.
כדי לקבל תמונה ברורה יותר של מה שמתרחש במעגל כזה, נשרטט את הגרפים הסינוסואידיים של ו-. הערכים המקסימליים הם בהתאמה ו-, משום שכפי שנאמר קודם לכן, ו- הם ערכים אפקטיביים. על ידי כפל הערכים הרגעיים של המתח והזרם נקבל את ההספק הרגעי ב-.

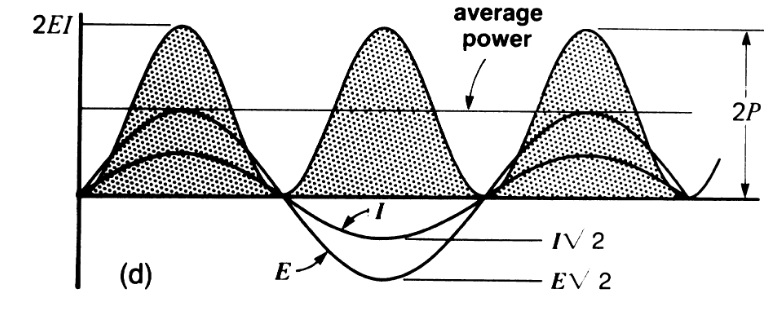
ההספק הפעיל מורכב מסדרה של פולסי כוח חיוביים. (Wildi, 2014).

גל ההספק מורכב מסדרה של פולסים חיוביים שמשתנים מאפס ועד לערך מקסימלי של . העובדה שההספק תמיד חיובי מצביעה על כך שהוא תמיד זורם מהגנרטור אל הנגד. זו אחת מהתכונות הבסיסיות של מה שנקרא הספק פעיל: למרות שהוא פועם בין אפס למקסימום, הוא אף פעם לא משנה כיוון.

ההספק הממוצע נמצא בבירור באמצע בין לאפס, ולכן ערכו הוא . זה בדיוק הערך שמוצג על ידי מד-ההספק (wattmeter). שני המוליכים שמובילים לנגד באיור הראשון נושאים את ההספק הפעיל. אולם, בשונה מזרם, ההספק לא זורם דרך מוליך אחד וחוזר דרך השני. ההספק זורם דרך שני המוליכים יחד, ולכן, מבחינת ההספק, ניתן להחליף את שני המוליכים בקו יחיד, כפי שמוצג באיור הבא:

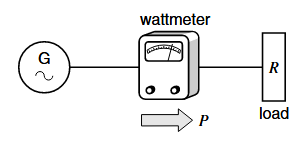
מד-הספק. (Wildi, 2014).

באופן כללי, הקו מייצג כל קו הולכה שמחבר בין שני מכשירים, בלי קשר למספר המוליכים שבו. הגנרטור הוא מקור פעיל והנגד הוא עומס פעיל. הסמל של ההספק הפעיל הוא והיחידה היא .

הספק הגבי

המעגל באיור הבא זהה למעגל ההתנגדות הקודם, פרט לכך שכעת הנגד הוחלף בריאקטור ​.

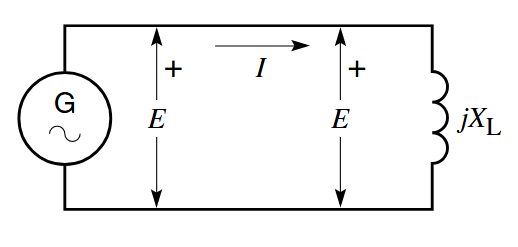
מקור מתח חילופין יוצר זרם חילופין במעגל עם סליל. (Wildi, 2014).

כתוצאה מכך, הזרם מאחר ב- אחרי המתח . (Wildi, 2014).

פאזור מאחר ב- אחרי המתח . (Wildi, 2014).

כדי להבין מה קורה באמת במעגל כזה, שרטטנו את גלי ו-, ושוב, על ידי כפל הערכים הרגעיים שלהם, קיבלנו את הגרף של ההספק הרגעי:

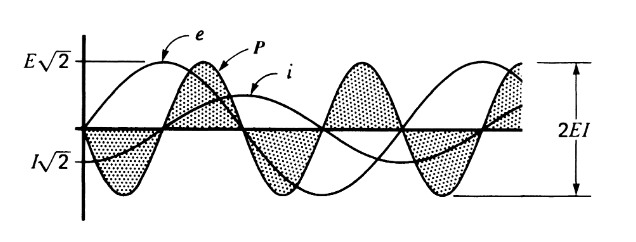
הספק הגבי מורכב מסדרה של פולסים חיוביים ושליליים. (Wildi, 2014).

הספק זה מורכב מסדרה של פולסים חיוביים ושליליים זהים. הגלים החיוביים מייצגים הספק רגעי המסופק מהגנרטור לריאקטור, והגלים השליליים מייצגים הספק רגעי שחוזר מהריאקטור לגנרטור. משך כל גל תואם לרבע מחזור של תדר הרשת. לכן, גם כאן תדר גל ההספק הוא פי שתיים מתדר הרשת.

הספק שזז הלוך ושוב בצורה כזו נקרא הספק הגבי , כדי להבדילו מההספק החד-כיווני שהוזכר קודם לכן. ההספק הגבי באיור לעיל ניתן גם הוא על ידי המכפלה . עם זאת, כדי להבדילו מההספק הפעיל, נעשה שימוש ביחידה שונה – ואר (var). היחידות הנפוצות הנגזרות ממנה הן קילוואר ומגהואר .

מכשירים מיוחדים הנקראים וַרמטרים (varmeters) משמשים למדידת הספק הגבי במעגל.

ורמטר המסוגל למדוד הספק הגבי שלילי וחיובי עד ל-. (Wildi, 2014).

הורמטר מציג את המכפלה של המתח האפקטיבי בזרם האפקטיבי וב-, כאשר היא זווית הפאזה בין ו-. מתקבלת קריאה רק כאשר ו- אינם באותו מופע; אם הם באותו מופע בדיוק (או הפוכים ), הורמטר יציג אפס.

אם נחזור לגרף האחרון, השטח המנוקד שמתחת לכל פולס מייצג את האנרגיה, ביחידות , המועברת לכיוון אחד או לשני. ברור כי האנרגיה מועברת כסדרה רציפה של פולסים קצרים מאוד, כאשר כל פולס חיובי מלווה מיד בפולס שלילי. האנרגיה זורמת הלוך ושוב בין הגנרטור לסליל מבלי להיצרך בפועל.

מה הסיבה לזרמים החוזרים של אנרגיה חיובית ושלילית אלה? האנרגיה נעה קדימה ואחורה משום שאנרגיה מגנטית נאגרת ומשתחררת לסירוגין בתוך הריאקטור. כלומר, כאשר ההספק חיובי, השדה המגנטי בתוך הסליל הולך ונבנה. רגע לאחר מכן, כשההספק הופך לשלילי, האנרגיה שבשדה המגנטי פוחתת וזורמת חזרה אל המקור.

כעת יש לנו הסבר לפולסים הקצרים של הספק שלילי שהופיעו בגרף הראשון. למעשה, הם מייצגים אנרגיה מגנטית שנאגרה קודם לכן בליפופי המנוע – וכעת חוזרת אל המקור.

קבל והספק הגבי

נניח כעת שאנו מוסיפים קבל בעל ריאקטנס (החלק המדומה של האימפידנס) של למעגל הקודם. מתקבל המעגל הבא:

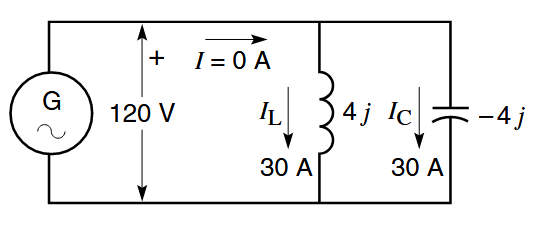
מקור מתח חילופין יוצר זרם חילופין במעגל עם סליל וקבל. (Wildi, 2014).

הזרם שזורם דרך הקבל הוא , וכפי שנצפה, הוא מקדים את המתח ב-:

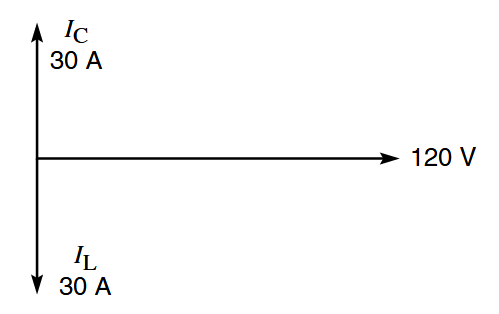
פאזור מאחר ב- אחרי המתח , בעוד מקדים ב- את . (Wildi, 2014).

הסכום הוקטורי של ו- הוא אפס, ולכן הגנרטור אינו מספק עוד הספק למעגל. עם זאת, הזרם בסליל לא השתנה; לכן, הוא ממשיך “לצרוך” של הספק הגבי. מהיכן מגיע הספק זה? הוא יכול להגיע רק מהקבל, אשר מתפקד כמקור של הספק הגבי.

ההספק ההגבי שמספק הקבל שווה לזרם שהוא מעביר כפול המתח על הדקיו:

כעת זורם הספק הגבי מהקבל לסליל. הגענו למסקנה חשובה: קבל הוא מקור של הספק הגבי. הוא מתפקד כמקור הספק הגבי בכל מעגל סינוסואידי במצב יציב.

נמשיך צעד נוסף ונוציא את הסליל מהמעגל, כך שמתקבל המעגל הבא:

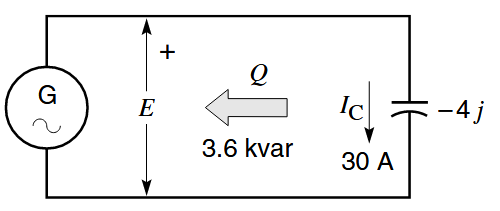
מקור מתח חילופין יוצר זרם חילופין במעגל עם קבל. (Wildi, 2014).

הקבל כעת מחובר לבדו לגנרטור AC. הוא עדיין מעביר זרם של , שמקדים את המתח ב-. לכן, הקבל ממשיך לתפקד כמקור של הספק הגבי ומספק . לאן הולך הספק זה? התשובה היא שהקבל מספק הספק הגבי לגנרטור עצמו שאליו הוא מחובר:

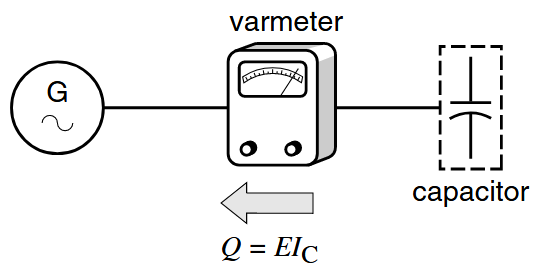
הספק הגבי זורם מהקבל לגנרטור. (Wildi, 2014).

עבור רבים, זה עשוי להיראות מוזר – כיצד רכיב פסיבי כמו קבל יכול “לייצר” הספק? התשובה היא שהספק הגבי מייצג אנרגיה שנעה הלוך ושוב, בדומה למטוטלת, מבלי לבצע עבודה שימושית. הקבל משמש כאוגר אנרגיה זמני: הוא קולט אנרגיה לפרקי זמן קצרים ומשחרר אותה שוב, אך במקום לאגור אנרגיה מגנטית כמו סליל, הוא אוגר אנרגיה אלקטרוסטטית.
לסיכום, ריאקטנס קיבולי תמיד מייצר הספק הגבי.

הבחנה בין הספק פעיל להספק הגבי

קיימת הבחנה בסיסית בין הספק פעיל להספק הגבי, ואולי הדבר החשוב ביותר לזכור הוא שאי אפשר להמיר אחד לשני. הספק פעיל והספק הגבי פועלים באופן בלתי תלוי זה בזה, ולכן ניתן להתייחס אליהם כאל גדלים נפרדים במעגלים חשמליים. שניהם מעמיסים על קווי ההולכה שמעבירים אותם, אך בעוד שהספק פעיל בסופו של דבר יוצר תוצאה מוחשית (חום, הספק מכני, אור וכדומה), הספק הגבי מייצג רק הספק שנע הלוך ושוב.

כל המכשירים האינדוקטיביים בזרם חילופין, כגון מגנטים, שנאים, ומנועים אינדוקציוניים, צורכים הספק הגבי משום שאחד מרכיבי הזרם שהם מושכים מאחר ב- אחרי המתח. להספק הגבי תפקיד חשוב מאוד, שכן הוא יוצר את השדה המגנטי במכשירים אלה.

כל בניין, מרכז קניות או עיר שלמה ניתן לראות כעומס ענק של הספק פעיל והספק הגבי המחובר לרשת החשמל. מרכזי עומס כאלה מכילים אלפי מנועים אינדוקציוניים ומכשירים אלקטרומגנטיים נוספים, שצורכים גם הספק הגבי (לשמירה על השדות המגנטיים שלהם) וגם הספק פעיל (לביצוע העבודה השימושית). מכאן נובע הצורך ללמוד עומסים שצורכים גם הספק פעיל וגם הספק הגבי.

הספק נדמה

עומסים שצורכים גם הספק פעיל וגם הספק הגבי ניתנים לייצוג כהרכבה של נגד וריאקטנס אינדוקטיבי. לדוגמה, במעגל שבאיור הבא, נגד וריאקטור מחוברים למקור .

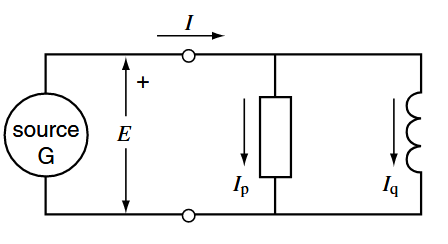
סליל ונגד במעגל AC. מ-(Wildi, 2014).

הנגד מושך זרם והריאקטור מושך זרם . לפי ההגדרות שלנו, הנגד הוא עומס פעיל והריאקטור הוא עומס הגבי. לכן, נמצא במופע עם ואילו מאחר ב- אחרי .

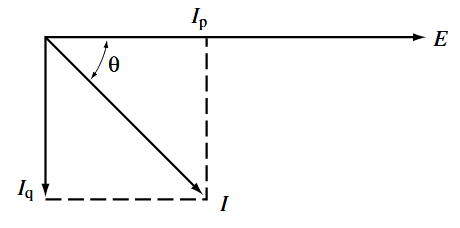
דיאגרמת פאזורים למעגל לעיל. (Wildi, 2014).

דיאגרמת הפאזורים מראה כי הזרם הכולל מאחר אחרי בזווית כלשהי. גודלו של ניתן על ידי:

רכיבי ההספק הפעיל וההספק ההגבי ( ו-) זורמים שניהם באותו כיוון, כפי שמוצג בחצים באיור הבא:

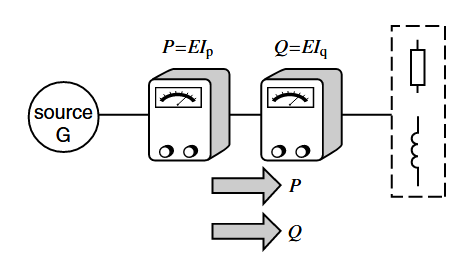
הספק הגבי ופעיל הזורם מהגנרטור לעומס. (Wildi, 2014).

אם נחבר מד-הספק (wattmeter) ו-ורמטר (varmeter) למעגל, הקריאות יהיו חיוביות: ו-, בהתאמה. אם נחבר אמפרמטר לקו, הוא יציג זרם אמפר.

כתוצאה מכך, ייתכן שנחשוב שההספק המסופק לעומס הוא , אך זה אינו נכון, כי ההספק מורכב מרכיב פעיל () ורכיב הגבי (). לכן, המכפלה נקראת הספק נדמה. הסימון להספק נדמה הוא . הספק נדמה אינו נמדד בוואט או בוור, אלא ביחידות של וולט-אמפר ().

הקשר בין P, Q ו-S

נבחן את המעגל החד-פאזי שבאיור הבא המורכב ממקור, עומס ומדי מדידה מתאימים.

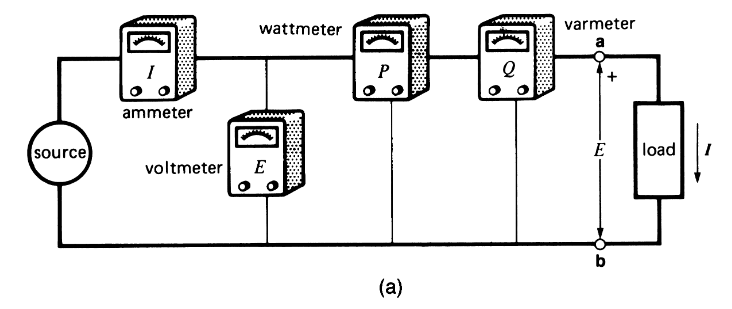
מכשירים למדידת ו- במעגל. (Wildi, 2014).

נניח כי:

• הוולטמטר מציג וולט
• האמפרמטר מציג אמפר
• מד-הספק (wattmeter) מציג וואט
• הורמטר (varmeter) מציג ואר

בהנחה ש- ו- חיוביים, ברור שהעומס צורך גם הספק פעיל וגם הספק הגבי. לכן, זרם הקו מאחר אחרי בזווית כלשהי. ניתן לפרק את הזרם לשני רכיבים: (במופע עם ) ו- (מאחר ב- אחרי ).

הערכים המספריים של ו- ניתנים לחישוב ישירות מקריאות המכשירים:

ההספק הנדמה המועבר הוא ולכן:

ראינו כבר כי:

ולכן:

או פשוט:

כאשר:

מקדם הספק (Power Factor)

מקדם ההספק של מכשיר או מעגל זרם חילופין הוא היחס בין ההספק הפעיל לבין ההספק הנדמה :

כאשר:

• הוא ההספק הפעיל המסופק או הנספג על ידי המעגל או המכשיר
• הוא ההספק הנדמה של המעגל או המכשיר

מקדם ההספק מבוטא כמספר פשוט (ללא יחידות) או כאחוז. מכיוון שההספק הפעיל לעולם אינו יכול לעלות על ההספק הנדמה , מקדם ההספק לעולם אינו גדול מ- או .

לנגד טהור, מקדם ההספק הוא , כי ההספק הנדמה שווה להספק הפעיל. לעומת זאת, לסליל אידיאלי ללא התנגדות, מקדם ההספק הוא אפס, כי הוא אינו צורך הספק פעיל כלל.
לסיכום, מקדם ההספק של מעגל או מכשיר מבטא איזה חלק מההספק הנדמה הוא הספק אמיתי (פעיל).
במעגל חד-פאזי, מקדם ההספק הוא גם מדד לזווית הפאזה בין המתח לזרם:

ולפיכך:

אם ידוע מקדם ההספק, ידוע גם הקוסינוס של הזווית בין ל-, ולכן ניתן לחשב את הזווית עצמה. מקובל לומר שמקדם ההספק הוא “מאחר” (lagging) כאשר הזרם מאחר אחרי המתח, ו”מקדים” (leading) כאשר הזרם מקדים את המתח.