ELM1_003 עקרונות המרת אנרגיה אלקטרומכנית

מתוך (Umans & Fitzgerald, 2014):

מבוא

בפרק זה נדון בתהליך המרת האנרגיה האלקטרומכנית, המתרחש באמצעות שדה חשמלי או מגנטי. התקני ההמרה, על אף פעולתם על עקרונות דומים, נבדלים במבניהם בהתאם לייעודם. ניתן לחלקם לשלוש קטגוריות עיקריות:

• מתמרים (Transducers): התקנים למדידה ובקרה, כגון מיקרופונים, חיישנים ורמקולים. הם פועלים לרוב בתנאים ליניאריים עם אותות קטנים.
• התקנים מפיקי כוח: כגון סולנואידים, ממסרים ואלקטרומגנטים.
• ציוד להמרת אנרגיה רציפה: כגון מנועים וגנרטורים.

כוחות ומומנטים במערכות שדה מגנטי

הגדרה:

כוח לורנץ הפועל על חלקיק בעל מטען בנוכחות שדות חשמליים ומגנטיים ניתן על ידי:

כאשר:

• הוא הכוח ביחידות ניוטון ().
• הוא המטען ביחידות קולון ().
• היא עוצמת השדה החשמלי ביחידות וולט למטר ().
• היא צפיפות השטף המגנטי ביחידות טסלה ().
• היא מהירות החלקיק יחסית לשדה המגנטי ביחידות מטר לשנייה ().

במערכת שדה חשמלי טהור (כלומר, ), הכוח על החלקיק הוא:

הכוח פועל בכיוון השדה החשמלי ואינו תלוי בתנועת החלקיק.

במערכת שדה מגנטי טהור (כלומר, ), הכוח על החלקיק הוא:

כוח זה תלוי בגודל המטען, בגודל השדה המגנטי ובמהירות החלקיק. כיוון הכוח תמיד ניצב לכיוון תנועת החלקיק ולכיוון השדה המגנטי.

כאשר מדובר במספר גדול של חלקיקים טעונים בתנועה, נוח לבטא את כוח לורנץ באמצעות צפיפות המטען (ביחידות ). צפיפות הכוח (כוח ליחידת נפח, ביחידות ) היא:

המכפלה מוגדרת כצפיפות הזרם (ביחידות ):

לכן, במערכת מגנטית (שבה ), צפיפות הכוח הנובעת מזרמים בתווך מוליך היא:

משוואה זו מאפשרת לחשב את צפיפות הכוח הפועלת על החומר המוליך עצמו.

הערה

חשוב לציין כי מאחורי הקשר הפשוט לכאורה במשוואה מסתתר מנגנון פיזיקלי מורכב המתאר כיצד הכוח מועבר מהמטענים הנעים אל התווך המוליך.

מאזן אנרגיה ושיטת האנרגיה

טכניקות לחישוב מפורט של כוחות מקומיים הפועלים במערכות עם חומרים מגנטיים הן מורכבות ביותר ודורשות ידע מפורט של התפלגות השדה במבנה. למרבה המזל, רוב התקני המרת האנרגיה האלקטרומכנית בנויים ממבנים קשיחים שאינם מתעוותים. ביצועי התקנים אלו נקבעים בדרך כלל על ידי הכוח השקול, או המומנט השקול, הפועל על הרכיב הנע, ולרוב אין צורך לחשב את פרטי התפלגות הכוחות הפנימית.

לדוגמה, במנוע מתוכנן כהלכה, מאפייני המנוע נקבעים על ידי מומנט התאוצה השקול הפועל על הרוטור; כוחות נלווים, הפועלים למעיכה או לעיוות של הרוטור, אינם משחקים תפקיד משמעותי בביצועי המנוע ובדרך כלל אינם מחושבים.

ניתן לדמיין זאת כך: לרוטור ולסטטור (החלק הקבוע במנוע/גנרטור) יש שדות מגנטיים (הנוצרים לרוב על ידי זרמים בסלילים). שני סטים אלו של שדות מגנטיים שואפים להתיישר זה עם זה, והמומנט נוצר כתוצאה מהסטייה שלהם מהתיישרות. במנוע, השדה המגנטי של הסטטור מסתובב לפני זה של הרוטור, מושך אותו ומבצע עבודה. בגנרטור, המצב הפוך – הרוטור מבצע עבודה על הסטטור.

נתחיל מעיקרון שימור האנרגיה, הקובע שאנרגיה אינה נוצרת או נהרסת; היא רק משנה צורה. עבור מערכות מבודדות עם גבולות מוגדרים בבירור, עובדה זו מאפשרת לנו לעקוב אחר האנרגיה בפשטות: זרימת האנרגיה נטו אל המערכת דרך גבולותיה שווה לסכום קצבי השינוי בזמן של האנרגיה האגורה במערכת.

שיטת האנרגיה, המשמשת לחישוב כוחות ומומנטים בתהליך המרת האנרגיה האלקטרומכנית, מבוססת על עיקרון שימור האנרגיה (החוק הראשון של התרמודינמיקה). במערכות אלקטרומכניות שבהן מנגנון אגירת האנרגיה העיקרי הוא בשדות מגנטיים, ניתן לתאר את מעבר האנרגיה כך:

משוואה מנוסחת כך שבמקרה של מנוע, הן לאנרגיה החשמלית והן לאנרגיה המכנית יש ערכים חיוביים (הספק חשמלי נכנס מומר להספק מכני יוצא). במקרה של גנרטור (הספק מכני נכנס מומר להספק חשמלי יוצא), שני האיברים הללו שליליים. בכל מקרה, ייצור חום במערכת גורם לזרימת אנרגיה תרמית אל מחוץ למערכת.

במערכות הנדונות כאן, המרת אנרגיה לחום מתרחשת במנגנונים כמו הספק חום מהתנגדות עקב זרימת זרם בסלילים וחיכוך מכני. לרוב ניתן להפריד מתמטית מנגנוני הפסד אלו ממנגנון אגירת האנרגיה. במקרים כאלה, האינטראקציה בין הדקי החשמל וההדקים המכניים, כלומר המרת האנרגיה האלקטרומכנית, מתרחשת באמצעות האנרגיה המגנטית האגורה, וניתן לייצג את ההתקן כמערכת אגירת אנרגיה חסרת הפסדים עם הדקים חשמליים ומכניים, כמתואר באיור הבא:

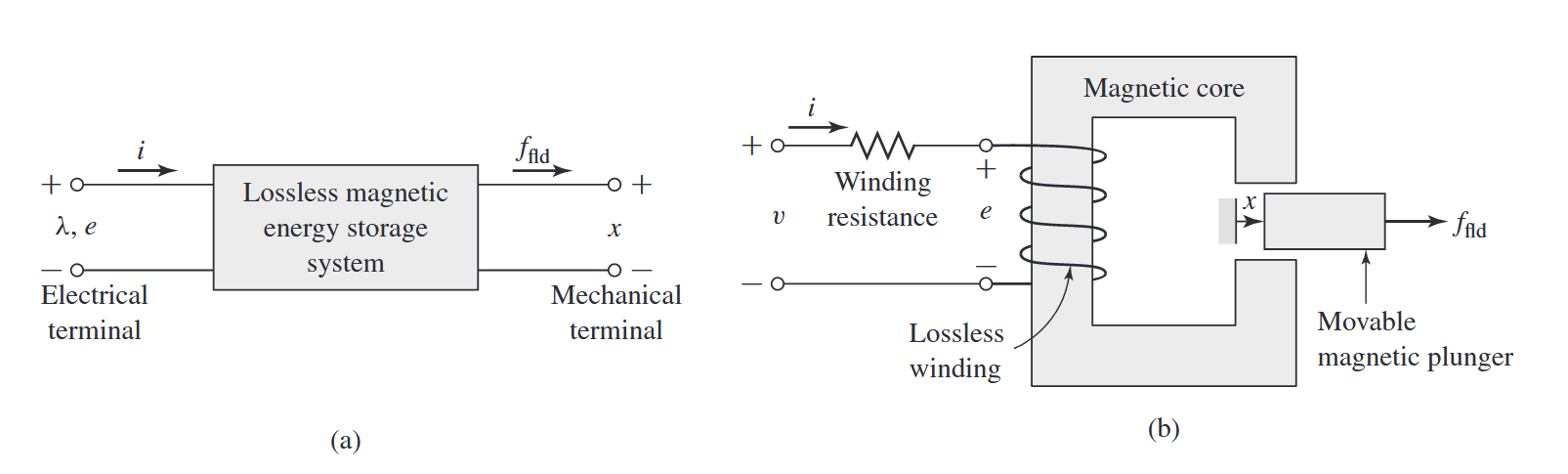
ב-(a) תיאור סכמטי של התקן המרת אנרגיה אלקטרומכנית מבוסס שדה מגנטי; (b) מכשיר פשוט המפיק כוח.(Umans & Fitzgerald, 2014).

במערכות הניתנות למודל באופן זה, ניתן לייצג מנגנוני הפסד על ידי רכיבים חיצוניים המחוברים להדקים אלו: נגדים להדקים החשמליים, ובולמי זעזועים מכניים להדקים המכניים. אין צורך להתחשב בהפסדים אלו בחישובים הנוגעים לתהליך המרת האנרגיה האלקטרומכנית. חלק (b) באיור לעיל מציג דוגמה למערכת כזו: התקן פשוט מפיק כוח עם סליל יחיד היוצר את ההדק החשמלי, ובוכנה מגנטית נעה המשמשת כהדק המכני.

מהות שיטת האנרגיה

היכולת לזהות מערכת אגירת אנרגיה חסרת הפסדים היא מהות שיטת האנרגיה. חשוב להכיר בכך שזה נעשה מתמטית כחלק מתהליך המידול. לא ניתן, כמובן, להסיר את ההתנגדות מהסלילים או את החיכוך מהמסבים. במקום זאת, אנו משתמשים בעובדה שמודל שבו זה נעשה מהווה ייצוג תקין של המערכת הפיזיקלית.

עבור מערכת אגירת אנרגיה חסרת הפסדים, ניתן לכתוב את משוואה כך:

כאשר:

• הוא ההספק החשמלי הנכנס.
• הוא ההספק המכני היוצא.
• הוא קצב השינוי בזמן של האנרגיה המגנטית האגורה.

באיור (a) לעיל, להדק החשמלי שני משתני הדק, מתח וזרם , ולהדק המכני גם שני משתני הדק, כוח ומיקום .
ההספק החשמלי הנכנס ניתן לכתיבה כמכפלת המתח והזרם :

וההספק המכני היוצא ניתן לכתיבה כמכפלת הכוח והמהירות (הנגזרת בזמן של המיקום ):

לאחר סידור מחדש של משוואה והצבת משוואות ו- נקבל:

עבור מערכת אגירת אנרגיה מגנטית, ההדק החשמלי מייצג בדרך כלל סליל כפי שמוצג באיור (b). מתוך השראות, המתח בהדקי סליל חסר הפסדים ניתן על ידי הנגזרת בזמן של סך השטף דרך כל הכריכות של הסליל:

כאשר ו- הוא השטף המגנטי בסליל.
הצבה במשוואה והכפלה ב- נותנת:

כפי שיוצג בהמשך, משוואה מאפשרת לנו לפתור עבור הכוח כפונקציה של כריכות השטף ומיקום ההדק המכני .

הערה

תוצאה זו נובעת מהנחתנו כי ניתן להפריד את ההפסדים מהבעיה הפיזיקלית, וכתוצאה מכך לקבל מערכת אגירת אנרגיה חסרת הפסדים. משוואות ו- מהוות את הבסיס לשיטת האנרגיה. טכניקה זו חזקה מאוד ביכולתה לחשב כוחות ומומנטים במערכות המרת אנרגיה אלקטרומכניות מורכבות. עם זאת, יש להכיר בכך שכוח זה בא על חשבון תמונה מפורטת של מנגנון יצירת הכוח. הכוחות עצמם נוצרים על ידי תופעות פיזיקליות ידועות כמו כוח לורנץ על רכיבים נושאי זרם (משוואה ), והאינטראקציה של השדות המגנטיים עם הדיפולים בחומר המגנטי.

אנרגיה במערכות שדה מגנטי עם עירור יחיד

בנושאים הקודמים עסקנו בעיקר במעגלים מגנטיים בעלי גאומטריה קבועה, כמו אלו המשמשים בשנאים ובמשרנים. האנרגיה בהתקנים אלו נאגרת בשדות הזליגה ובמידה מסוימת בליבה עצמה. עם זאת, האנרגיה האגורה אינה משתתפת ישירות בתהליך ההתמרה. בפרק זה אנו עוסקים במערכות המרת אנרגיה; למעגלים המגנטיים יש מרווחי אוויר בין החלקים הנייחים והנעים, שבהם נאגרת אנרגיה ניכרת בשדה המגנטי. שדה זה משמש כתווך להמרת האנרגיה, והאנרגיה שלו מהווה את המאגר בין המערכות החשמלית והמכנית.

נתבונן ב**מִמְסָר (relay)** האלקטרומגנטי המוצג סכמטית באיור הבא:

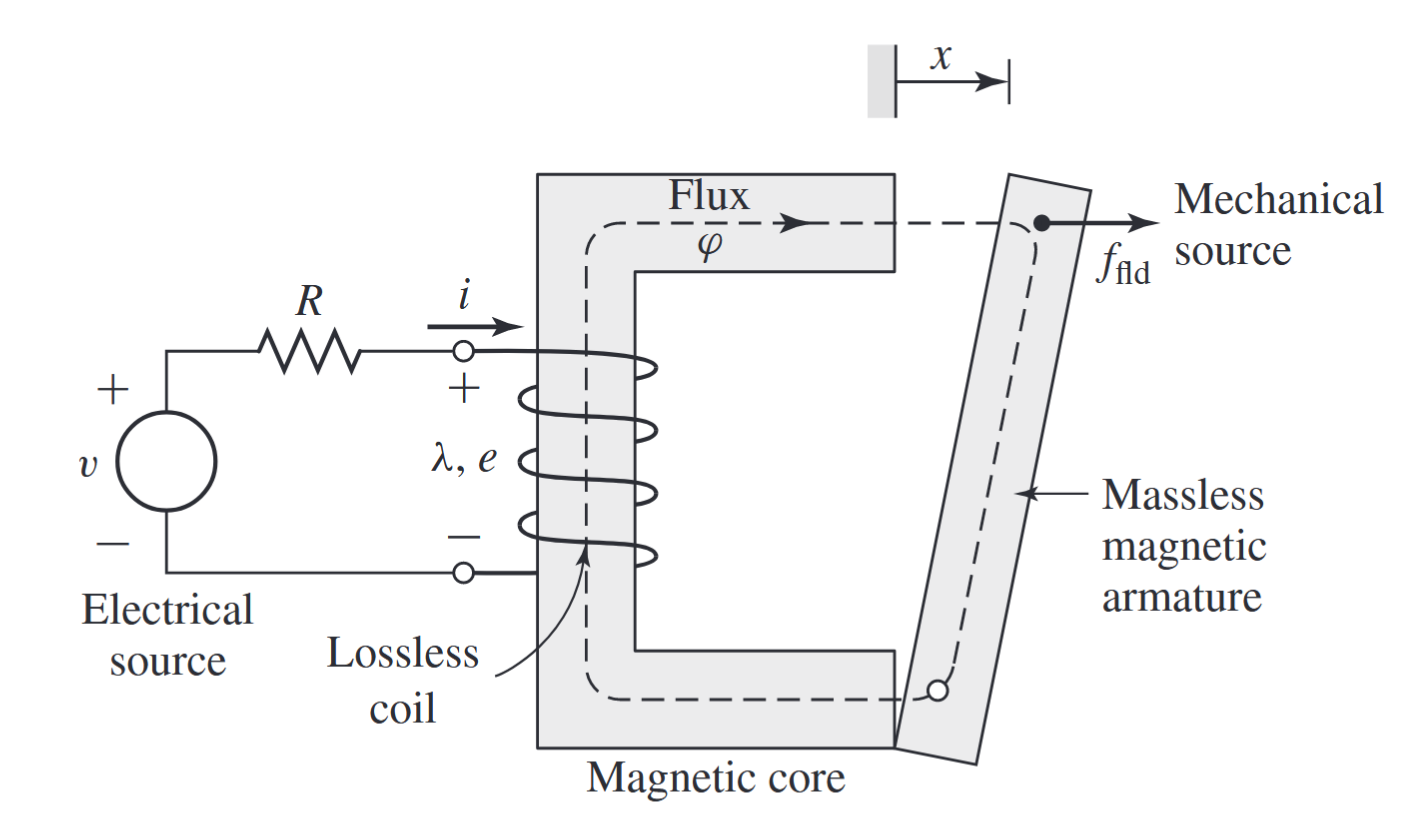
תיאור סכמטי של ממסר אלקטרומגנטי. (Umans & Fitzgerald, 2014).

התנגדות סליל העירור מוצגת כהתנגדות חיצונית , ומשתני ההדק המכני מוצגים ככוח המופק על ידי השדה המגנטי, הפועל מהממסר אל המערכת המכנית החיצונית, ותזוזה . הפסדים מכניים יכולים להיכלל כרכיבים חיצוניים המחוברים להדק המכני. באופן דומה, העוגן הנע מוצג כחסר מסה; מסתו מייצגת אגירת אנרגיה מכנית וניתן לכלול אותה כמסה חיצונית המחוברת להדק המכני. כתוצאה מכך, הליבה המגנטית והעוגן מהווים מערכת אגירת אנרגיה מגנטית חסרת הפסדים.

מבנה ממסר זה דומה במהותו למבנים המגנטיים שניתחנו בפרק הראשון, שם ראינו שניתן לתאר את המעגל המגנטי של איור האיור לעיל באמצעות השראות שהיא פונקציה של גאומטריית המבנה המגנטי והפרמביליות המגנטית של רכיבי המערכת השונים. התקני המרת אנרגיה אלקטרומכנית מכילים מרווחי אוויר במעגלים המגנטיים שלהם כדי להפריד בין החלקים הנעים. ברוב המקרים הללו הרילקטנס (התנגדות מגנטית) של מרווח האוויר גדולה בהרבה מזו של החומר המגנטי. לפיכך, אגירת האנרגיה העיקרית מתרחשת במרווח האוויר, ותכונות המעגל המגנטי נקבעות על ידי מידות מרווח האוויר.

בשל פשטות הקשרים המתקבלים, אי-ליניאריות מגנטית והפסדי ליבה מוזנחים לעיתים קרובות בניתוח התקנים מעשיים. ניתן לתקן את התוצאות הסופיות של ניתוחים מקורבים כאלה, במידת הצורך, עבור השפעות גורמים אלו שהוזנחו, בשיטות חצי-אמפיריות. כתוצאה מכך, הניתוחים מבוצעים בהנחה שהכמ”מ (כוח מגנטו-מניע) והשטף נמצאים ביחס ישר עבור כל המעגל המגנטי. לפיכך, קישורי השטף והזרם נחשבים קשורים ליניארית על ידי השראות התלויה אך ורק בגאומטריה, ומכאן במיקום העוגן :

מכיוון שמערכת אגירת האנרגיה המגנטית היא חסרת הפסדים, היא מערכת משמרת, וערך נקבע באופן ייחודי על ידי ערכי ו-. לכן, ו- מכונים משתני מצב, שכן ערכיהם קובעים באופן ייחודי את מצב המערכת. מאחר שהכוח המגנטי הוגדר כפועל מהממסר על המערכת המכנית החיצונית, מוגדרת כאנרגיה המכנית היוצאת מהממסר, בהתאמה לפיתוחים קודמים ומשוואה , החוזרת כאן ומציגה במפורש את התלות של ב- ו-:

אנו רואים שהאנרגיה האגורה , הנקבעת באופן ייחודי על ידי ערכי ו-, לא תלויה באופן שבו ו- הגיעו לערכיהם הסופיים - יענו כוח משמר. נתבונן באיור הבא, שבו מוצגים שני מסלולים נפרדים שבאמצעותם ניתן לבצע אינטגרציה על משוואה כדי למצוא את בנקודה .

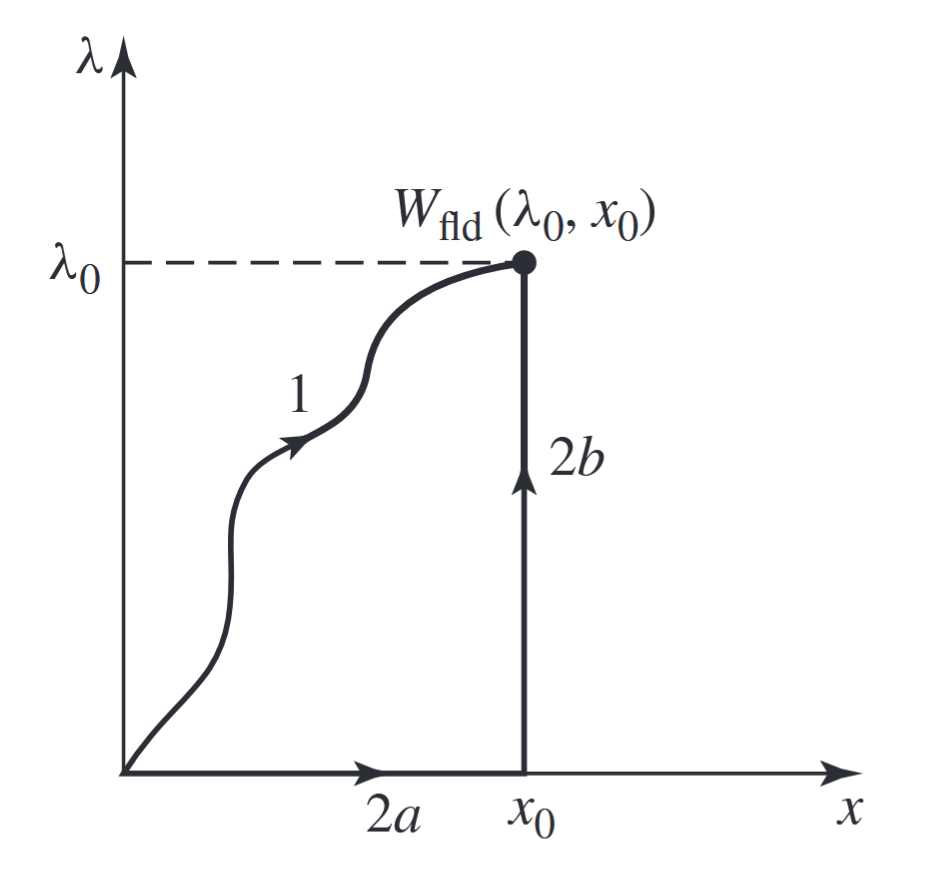
מסלולי אינטגרציה עבור . (Umans & Fitzgerald, 2014).

מסלול הוא המקרה הכללי וקשה לאינטגרציה אלא אם כן ו- ידועים במפורש כפונקציה של ו-. עם זאת, מכיוון שהאינטגרציה של משוואה אינה תלויה במסלול, מסלול נותן את אותה תוצאה והוא קל הרבה יותר לאינטגרציה:

שימו לב שבמסלול , מתקיים ו- (מכיוון ש- ולא יכול להיות כוח מגנטי בהיעדר שדות מגנטיים). לפיכך, ממשוואה , מתקיים במסלול . במסלול , מתקיים , ולכן, ממשוואה , במשוואה נישאר עם אינטגרל של על פני מסלול (שבו ):

עבור מערכת ליניארית שבה פרופורציונלי ל-, כמו במשוואה , משוואה נותנת:

שימו לב שהנקודה היא שרירותית; הביטוי עבור במשוואה תקף לכל הנקודות . כדי להדגיש נקודה זו, ניתן לכתוב את משוואה כך:

יואו, תראו, זה גם מה שקיבלנו באנרגיה אגורה במשרן.

ניתן לבטא את האנרגיה האגורה גם באמצעות מספר הכריכות , הזרם והרילקטנס של המעגל המגנטי. מהצבת במשוואה מקבלים . בהמשך, באמצעות הקשר , מתקבל:

ניתן להראות שניתן לבטא את האנרגיה המגנטית האגורה גם במונחים של צפיפות האנרגיה של השדה המגנטי שעברה אינטגרציה על נפח של השדה המגנטי. במקרה זה:

עבור חומר מגנטי רך בעל פרמיביליות קבועה (), זה מצטמצם ל:

קביעת כוח ומומנט מגנטיים מתוך אנרגיה

עבור מערכת אגירת אנרגיה מגנטית חסרת הפסדים, האנרגיה המגנטית האגורה היא פונקציית מצב, הנקבעת באופן ייחודי על ידי ערכי משתני המצב הבלתי תלויים ו-. הדבר מוצג במפורש במשוואה , החוזרת כאן:

עבור כל פונקציית מצב של שני משתנים בלתי תלויים, למשל , הדיפרנציאל השלם של ביחס לשני משתני המצב ו- ניתן לכתיבה כך:

חשוב ביותר להכיר בכך שהנגזרות החלקיות במשוואה מחושבות כל אחת כאשר משתנה המצב השני מוחזק קבוע. משוואה תקפה לכל פונקציית מצב , ולכן היא בוודאי תקפה עבור ; לפיכך:

מכיוון ש- ו- הם משתנים בלתי תלויים, משוואות ו- חייבות להיות שוות לכל ערכי ו-. לכן, על ידי השוואת מקדמים, אנו רואים כי:

וכן:

זו התוצאה שחיפשנו. ברגע שאנו יודעים את כפונקציה של ו-, ניתן להשתמש במשוואה כדי לפתור עבור . יתר על כן, ניתן להשתמש במשוואה כדי לפתור עבור הכוח המכני . הדבר נעשה בקלות בתנאי ש- היא פונקציה ידועה של ו-.

הכוח נקבע ממשוואה ישירות במונחי משתנה המצב החשמלי . אם לאחר מכן נרצה לבטא את הכוח כפונקציה של , נוכל לעשות זאת על ידי הצבת הביטוי המתאים עבור כפונקציה של בביטוי עבור המתקבל באמצעות משוואה . יש לשים לב כי הצבה זו חייבת להתבצע רק לאחר חישוב הנגזרת החלקית.

עבור מערכות מגנטיות ליניאריות שבהן , האנרגיה מבוטאת על ידי משוואה , והכוח ניתן למציאה על ידי הצבה ישירה במשוואה :

בנקודה זו, ניתן לבטא את הכוח במונחי הזרם פשוט על ידי הצבת :

ניתן לבטא את הכוח גם באמצעות מספר הכריכות , הזרם והרילקטנס של המעגל המגנטי. מהצבת ו- במשוואה מקבלים:

דוגמה: חישוב מומנט במעגל מגנטי עם רוטור

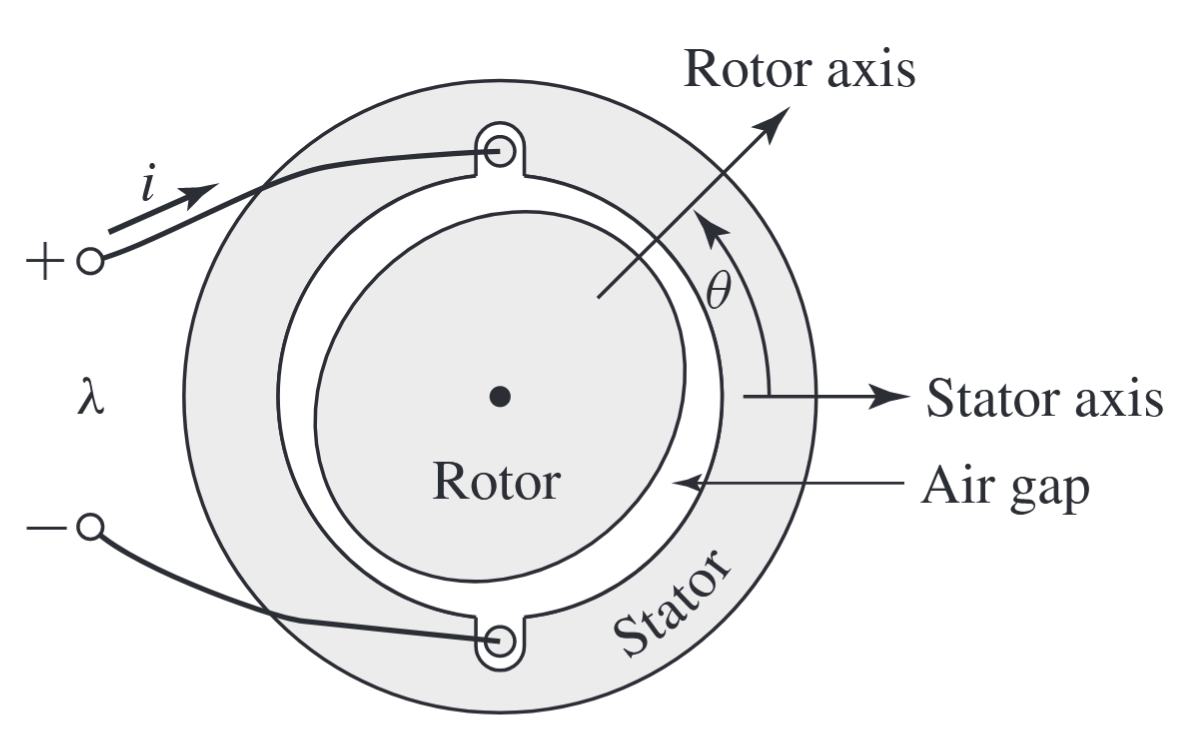
המעגל המגנטי באיור הבא מורכב מסטטור בעל סליל יחיד ורוטור אליפטי.

מעגל מגנטי עבור הדוגמה. (Umans & Fitzgerald, 2014).

מכיוון שמרווח האוויר אינו אחיד, השראות הסליל משתנה עם המיקום הזוויתי של הרוטור, , הנמדדת בין הציר המגנטי של סליל הסטטור לציר הראשי של הרוטור, לפי:

כאשר ו- .
שימו לב לווריאציה ההרמונית השנייה של ההשראות עם זווית הרוטור . הדבר עולה בקנה אחד עם העובדה שההשראות אינה משתנה אם הרוטור מסובב בזווית של .

שאלה:
מצאו את המומנט כפונקציה של עבור זרם סליל של .

פתרון:
עבור מערכת סיבובית עם השראות התלויה בזווית ותנועה סיבובית, המומנט המגנטי ניתן לחישוב מהאנרגיה האגורה בשדה המגנטי. נשתמש בכריכות השטף ובמיקום הזוויתי כמשתנים בלתי תלויים.
האנרגיה האגורה בשדה המגנטי, , עבור מערכת ליניארית מגנטית היא המקבילה הסיבובית של משוואה :

המומנט מתקבל מהנגזרת החלקית של האנרגיה האגורה לפי המיקום הזוויתי , כאשר כריכות השטף מוחזק קבוע. זהו המקביל הסיבובי של משוואה :

כעת, כדי לבטא את המומנט באמצעות הזרם , נשתמש בקשר . חשוב לבצע הצבה זו לאחר הגזירה החלקית:

שימו לב שמשוואה זו זהה לזו שהייתה מתקבלת משימוש בקו-אנרגיה (המקביל הסיבובי למשוואה ).

נחשב את הנגזרת של :

נציב בחזרה בביטוי למומנט:

נציב את הערכים ו- :

שימו לב שבמקרה זה המומנט פועל בכיוון כזה שישאף ליישר את ציר הרוטור עם ציר הסליל (כלומר, להקטין את לאפס).