ELM1_008 מנועי אינדוקציה

→ קודם: ELM1_007

מבוא

במנועי הזרם הישר (DC) שדנו בהם עד כה ולמנועים סינכרוניים יש דבר אחד משותף: שניהם הם מהסוג הזנה כפול. למנועים אלו זרם ישר בליפופי השדה שלהם וזרם חילופין (AC) בליפופי העוגן שלהם. מאחר שההספק החשמלי מועבר ישירות לעוגן של מנוע DC באמצעות קומוטטור, ניתן להתייחס אליו גם כמנוע הולכה. כעת אנו בוחנים מנוע שבו הרוטור מקבל את הכוח שלו לא על ידי הולכה אלא על ידי השראה ולכן נקרא מנוע השראה/אינדוקציה. ליפוף המקבל את הכוח שלו באופן בלעדי על ידי השראה מהווה שנאי. לכן, מנוע אינדוקציה הוא שנאי עם ליפוף משני מסתובב.

1. מנוע אינדוקציה הוא מנוע הזנה יחיד. לכן, הוא אינו דורש קומוטטור, טבעות החלקה או מברשות. למעשה, אין מגעים נעים בין הסטטור לרוטור. התוצאה היא מנוע אמין וכמעט ללא תחזוקה. היעדר מברשות מבטל את הפסד החשמלי עקב נפילת מתח המברשות והפסד המכני עקב חיכוך בין המברשות לקומוטטור או לטבעות ההחלקה. כך, למנוע אינדוקציה יש יעילות גבוהה יחסית.

2. מנוע אינדוקציה נושא זרם חילופין הן בליפופי הסטטור והן בליפופי הרוטור.

3. מנוע אינדוקציה הוא שנאי מסתובב שבו הליפוף המשני מקבל אנרגיה על ידי השראה בזמן שהוא מסתובב.

קיימים שני סוגים בסיסיים של מנועי אינדוקציה: מנועי אינדוקציה חד-פאזיים ומנועי אינדוקציה רב-פאזיים. מנועי אינדוקציה חד-פאזיים מועדפים ליישומים ביתיים. מספר רב של מנועים אלו נבנים בטווח הזעיר של כוח סוס. מצד שני, מנועי אינדוקציה רב-פאזיים מכסים את כל הספקטרום של דירוגי כוח הסוס ומותקנים רצוי במקומות שבהם מקור הספק רב-פאזי נגיש בקלות. בשל הייצור וההעברה הנרחבים של הספק תלת-פאזי, רוב מנועי האינדוקציה הרב-פאזיים הם מהסוג התלת-פאזי. בפרק זה, אנו מגבילים את הדיון שלנו באופן בלעדי למנועי אינדוקציה תלת-פאזיים. עם זאת, ניתן להרחיב בקלות את הפיתוח התיאורטי למנוע אינדוקציה n-פאזי כאשר .

מבנה

הרכיבים החיוניים של מנוע אינדוקציה הם סטטור ורוטור.

סטטור

החלק החיצוני (הנייח) של מנוע אינדוקציה נקרא הסטטור ונוצר על ידי ערימת למינציות פלדה דקות מחורצות בעלות פרמביליות גבוהה בתוך מסגרת פלדה או ברזל יצוק. המסגרת מספקת תמיכה מכנית למנוע. למרות שהמסגרת עשויה מחומר מגנטי, היא אינה מתוכננת לשאת שטף מגנטי. סלילים זהים מלופפים (או מוצבים) בחריצים ולאחר מכן מחוברים ליצירת ליפוף תלת-פאזי מאוזן.

רוטור

הרוטור מורכב גם מלמינציות פלדה דקות מחורצות בעלות פרמביליות גבוהה הנדחסות יחד על ציר. קיימים שני סוגי רוטורים: רוטור כלוב סנאי ורוטור מלופף.

הרוטור כלוב סנאי משמש בדרך כלל כאשר העומס דורש מומנט התנעה קטן. עבור מנועים קטנים, ליפוף כזה נוצק על ידי הכרחת חומר מוליך מותך (לעתים קרובות, אלומיניום) לתוך החריצים בתהליך יציקת תבנית. טבעות עגולות הנקראות טבעות קצה נוצרות גם בשני צידי הערימה. טבעות קצה אלו גורמות לקצר במוטות בשני קצות הרוטור. עבור מנועים גדולים, ליפוף כלוב הסנאי נוצר על ידי הכנסת מוטות מוליכים כבדים (בדרך כלל של נחושת, אלומיניום או סגסוגותיהם) לתוך החריצים ולאחר מכן ריתוכם או הברגתם לטבעות הקצה. לכל זוג קטבים יש כמה פאזות רוטור כמו שיש מוטות מכיוון שכל מוט מתנהג באופן עצמאי מהאחרים. נהוג להטות את למינציות הרוטור כדי להפחית הידבקות ורעש חשמלי במנוע.

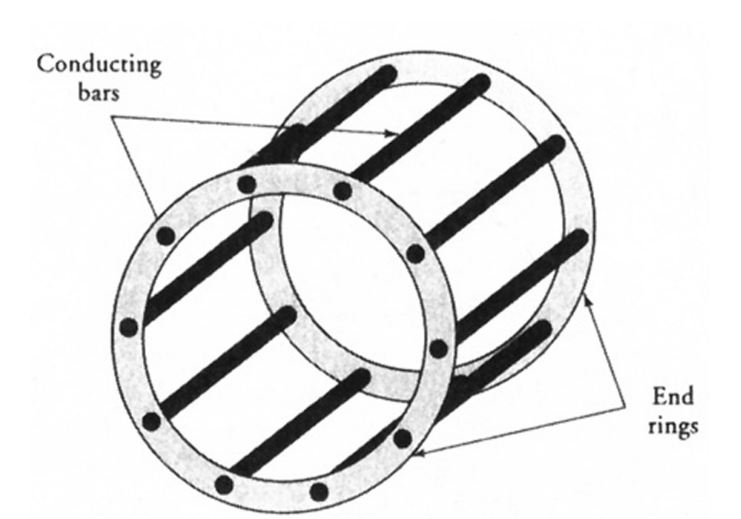
איור 8.1: ליפוף כלוב סנאי. (Guru, 2001).

יש צורך להשתמש ברוטור מלופף כאשר העומס דורש מומנט התנעה גבוה. רוטור מלופף חייב להיות בעל אותו מספר קטבים ופאזות כמו הסטטור. למעשה, מיקום הסלילים ברוטור מלופף אינו שונה מזה שבסטטור. שלושת הליפופים התלת-פאזיים על הרוטור מחוברים פנימית ליצירת חיבור נייטרלי פנימי. שלושת הקצוות האחרים מחוברים לטבעות ההחלקה. עם המברשות רוכבות על טבעות ההחלקה, אנו יכולים להוסיף התנגדויות חיצוניות במעגל הרוטור. בדרך זו ניתן לשלוט בהתנגדות הכוללת במעגל הרוטור. על ידי שליטה בהתנגדות במעגל הרוטור אנו, למעשה, שולטים במומנט המפותח על ידי המנוע. נראה שהמהירות שבה מנוע אינדוקציה מפתח את המומנט המקסימלי (הנקראת מהירות הפריצה) תלויה בהתנגדות הרוטור. ככל שהתנגדות הרוטור גדלה, מהירות הפריצה קטנה. לכן, ניתן לקבל מומנט מקסימלי בהתנעה (מהירות אפס) על ידי הכנסת כמות נכונה של התנגדות במעגל הרוטור. עם זאת, מנוע אינדוקציה רוטור מלופף יקר יותר ופחות יעיל ממנוע אינדוקציה כלוב סנאי באותו דירוג.

מסיבות אלו, מנוע אינדוקציה רוטור מלופף משמש רק כאשר מנוע אינדוקציה כלוב סנאי אינו יכול לספק את מומנט ההתנעה הגבוה הנדרש על ידי העומס.

עקרון הפעולה

כאשר ליפוף הסטטור של מנוע אינדוקציה תלת-פאזי מחובר למקור הספק תלת-פאזי, הוא יוצר שדה מגנטי ש-(א) קבוע בגודלו ו-(ב) מסתובב סביב היקף הרוטור במהירות הסינכרונית.

אם היא התדירות של הזרם בליפוף הסטטור ו- הוא מספר הקטבים, המהירות הסינכרונית של השדה המסתובב היא:

בסיבובים לדקה (), או

ברדיאנים לשנייה ().

השדה המסתובב משרה כוח אלקטרו-מניע (כא”מ) בליפוף הרוטור. מאחר שליפוף הרוטור יוצר לולאה סגורה, הכא”מ המושרה בכל סליל גורם לזרם מושרה באותו סליל. כאשר סליל נושא זרם שקוע בשדה מגנטי, הוא חווה כוח (או מומנט) הנוטה לסובב אותו. המומנט שמתפתח כך נקרא מומנט ההתנעה. אם מומנט העומס קטן ממומנט ההתנעה, הרוטור מתחיל להסתובב.

הכוח המפותח ובכך הסיבוב של הרוטור הם באותו כיוון של השדה המסתובב. זה בהתאם לחוק ההשראה של פאראדיי. תחת אפס עומס, הרוטור מגיע עד מהרה למהירות כמעט שווה למהירות הסינכרונית. עם זאת, הרוטור לעולם אינו יכול להסתובב במהירות הסינכרונית מכיוון שסלילי הרוטור יראו נייחים ביחס לשדה המסתובב ולא יהיה כא”מ מושרה בהם. בהיעדר כא”מ מושרה בסלילי הרוטור, לא יהיה זרם במוליכי הרוטור וכתוצאה מכך לא יחווה כוח. בהיעדר כוח, הרוטור יטה להאט. ברגע שהרוטור מאט, תהליך ההשראה משתלט שוב.

לסיכום, הרוטור מקבל את הכוח שלו על ידי השראה רק כאשר יש תנועה יחסית בין מהירות הרוטור לשדה המסתובב. מאחר שהרוטור מסתובב במהירות נמוכה יותר מהמהירות הסינכרונית של השדה המסתובב, מנוע אינדוקציה נקרא גם מנוע א-סינכרוני.

יהי (או ) מהירות הרוטור בעומס מסוים. ביחס למנוע, השדה המסתובב נע קדימה במהירות יחסית של:

או

כאשר הוא עבור relative.
המהירות היחסית נקראת גם מהירות ההחלקה. זוהי המהירות שבה הרוטור מחליק מאחורי נקודה על קוטב מסתובב פיקטיבי כדי לייצר מומנט. עם זאת, נהוג לבטא את מהירות ההחלקה במונחים של ההחלקה (), שהיא יחס מהירות ההחלקה למהירות הסינכרונית. כלומר:

למרות שהמשוואה לעיל מניבה את ההחלקה על בסיס יחידה, נהוג לבטא אותה כאחוז מהמהירות הסינכרונית (אחוז החלקה).

במונחים של המהירות הסינכרונית והחלקה ביחידה, אנו יכולים לבטא את מהירות הרוטור כ:

או

כאשר הרוטור נייח, ההחלקה ביחידה היא והרוטור נראה בדיוק כמו ליפוף משני קצור של שנאי. התדירות של הכא”מ המושרה בליפוף הרוטור זהה לזו של השדה המסתובב. עם זאת, כאשר הרוטור מסתובב, זוהי המהירות היחסית של הרוטור (או ) האחראית לכא”מ המושרה בליפופיו. כך, התדירות של הכא”מ המושרה ברוטור היא:

המשוואה לעיל מדגישה את העובדה שתדירות הרוטור תלויה בהחלקת המנוע. כאשר הרוטור נייח, ההחלקה היא ותדירות הרוטור זהה לזו של השדה המסתובב. עם זאת, תדירות הרוטור קטנה עם הקטנת ההחלקה. ככל שההחלקה מתקרבת לאפס, כך גם תדירות הרוטור. מנוע אינדוקציה פועל בדרך כלל בהחלקה נמוכה. לכן התדירות של הכא”מ המושרה ברוטור נמוכה. מסיבה זו, הפסד הליבה במעגל המגנטי של הרוטור מוזנח לרוב.

דוגמה:

איור 8.2: למנוע אינדוקציה תלת-פאזי בעל 4 קטבים, המופעל במתח ותדירות , מהירות מלא עומס של . חשבו:

1. את המהירות הסינכרונית

2. את ההחלקה, ו-

3. את תדירות הרוטור.

   פתרון:

4. המהירות הסינכרונית של מנוע האינדוקציה לפי משוואה (GU9.1a):

2. בעומס מלא, ההחלקה לפי משוואה (GU9.3):

3. תדירות הרוטור בעומס מלא לפי משוואה (GU9.5):

פיתוח מעגל שקול

כאשר מנוע אינדוקציה תלת-פאזי מאוזן מעורר על ידי מקור תלת-פאזי מאוזן, הזרמים בליפופי הפאזות חייבים להיות שווים בגודלם ומפוזרים ב- חשמליים במופע. הדבר חייב להיות נכון גם עבור הזרמים בליפופי הרוטור כאשר האנרגיה מועברת על פני רווח האוויר מהסטטור לרוטור על ידי השראה. עם זאת, תדירות הכא”מ המושרה ברוטור פרופורציונלי להחלקה שלו (משוואה (GU9.5)).

מאחר שליפופי הסטטור והרוטור מצומדים באופן אינדוקטיבי, מנוע אינדוקציה דומה לשנאי תלת-פאזי עם ליפוף משני מסתובב. הדמיון הופך אף יותר בולט כאשר הרוטור במנוחה (מצב רוטור חסום, ). לפיכך, ניתן לייצג מנוע אינדוקציה תלת-פאזי על בסיס פר-פאזה (לכל פאזה) על ידי מעגל שקול בכל החלקה כפי שמתואר באיור 8.1.

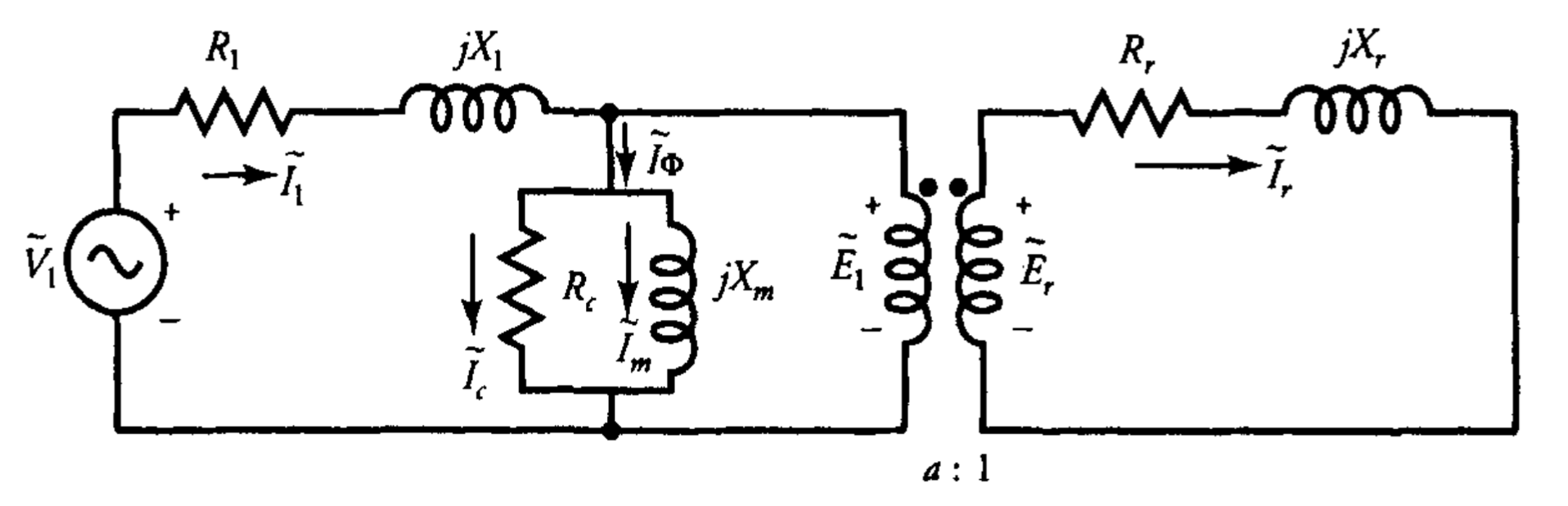
איור 8.3: מעגל שקול פר-פאזה של מנוע אינדוקציה תלת-פאזי מאוזן. (Guru, 2001).

באיור 8.1:

• - מתח מופעל על בסיס פר-פאזה
• - התנגדות ליפוף סטטור פר-פאזה
• - השראות זליגה ליפוף סטטור פר-פאזה
• - ריאקטנס זליגה ליפוף סטטור פר-פאזה
• - התנגדות ליפוף רוטור פר-פאזה
• - אינדוקטנס זליגה ליפוף רוטור פר-פאזה
• - ריאקטנס זליגה ליפוף רוטור פר-פאזה תחת מצב רוטור חסום ()
• - ריאקטנס זליגה ליפוף רוטור פר-פאזה בהחלקה
• - ריאקטנס מגנטיזציה פר-פאזה
• - התנגדות אובדני ליבה שקולה פר-פאזה
• - מספר כריכות אמיתי לפאזה של ליפוף הסטטור
• - מספר כריכות אמיתי לפאזה של ליפוף הרוטור
• - מקדם ליפוף עבור ליפוף הסטטור
• - מקדם ליפוף עבור ליפוף הרוטור
• - אמפליטודה של השטף פר-פאזה
• - כא”מ מושרה פר-פאזה בליפוף הסטטור
• - כא”מ מושרה פר-פאזה בליפוף הרוטור תחת מצב רוטור חסום ()
• - כא”מ מושרה פר-פאזה בליפוף הרוטור בהחלקה
• - זרם ליפוף רוטור פר-פאזה
• - זרם פר-פאזה המסופק על ידי המקור
• - זרם עירור פר-פאזה
• - זרם אובדני ליבה פר-פאזה
• - זרם מגנטיזציה פר-פאזה

מהאיור 8.1, ברור שהזרם במעגל הרוטור הוא:

על בסיס המשוואה לעיל, אנו יכולים לפתח מעגל אחר של מנוע אינדוקציה כפי שניתן באיור 8.2. במעגל זה, ההתנגדות ההיפותטית במעגל הרוטור נקראת ההתנגדות האפקטיבית. ההתנגדות האפקטיבית זהה להתנגדות הרוטור האמיתית כאשר הרוטור במנוחה (עמידה או מצב רוטור חסום). מצד שני, כאשר ההחלקה מתקרבת לאפס תחת מצב ללא עומס, ההתנגדות האפקטיבית גבוהה מאוד ().

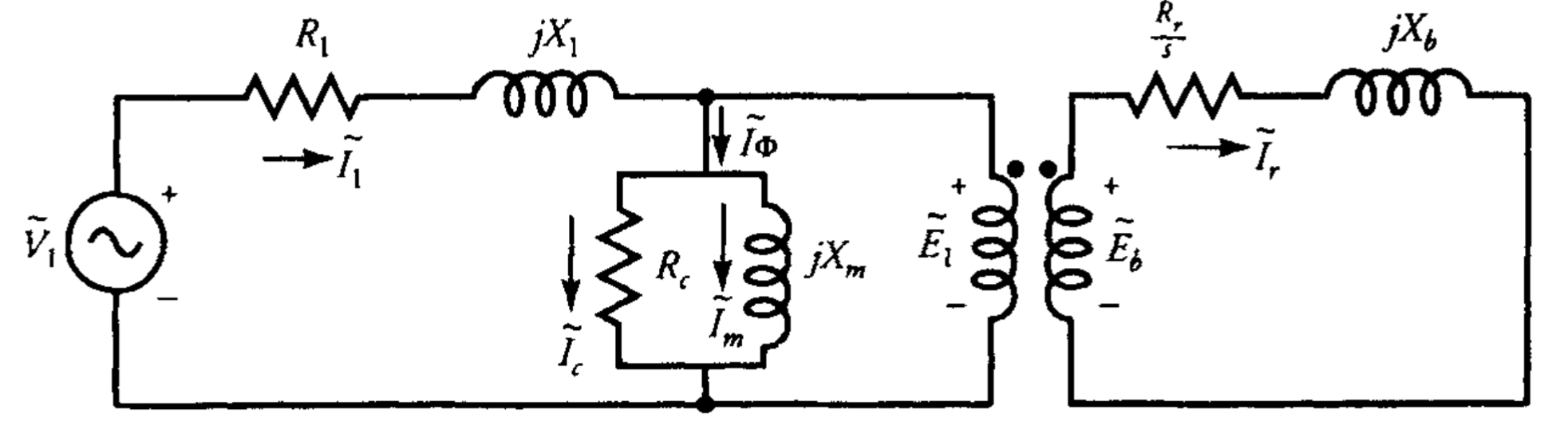
איור 8.4: מעגל שקול מעודכן של מנוע תלת-פאזי מאוזן על בסיס פר-פאזה. (Guru, 2001).

על ידי הגדרת יחס ההשנאה, יחס ה-, כ:

אנו יכולים לייצג את מנוע האינדוקציה על ידי המעגל השקול פר-פאזה שלו כפי שהוא מיוחס לסטטור. מעגל שקול כזה מוצג באיור 8.3, כאשר:

עבור מעגל שקול זה:

כאשר:

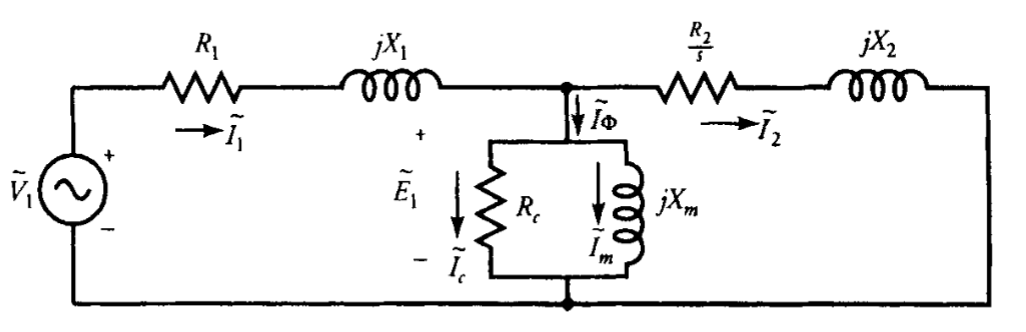
איור 8.5: מעגל שקול פר-פאזה של מנוע אינדוקציה תלת-פאזי מאוזן כפי שמיוחס לצד הסטטור. (Guru, 2001).

זרם ליפוף הסטטור פר-פאזה והמתח המופעל הם:

המעגל השקול של הרוטור באיור 8.3 הוא במונחים של ההתנגדות ההיפותטית . במעגל זה, מייצג את ההספק פר-פאזה המועבר לרוטור. עם זאת, הפסדי הנחושת פר-פאזה ברוטור חייבים להיות . לפיכך, ההספק פר-פאזה המפותח על ידי המנוע הוא:

או

המשוואה לעיל קובעת את העובדה שההתנגדות ההיפותטית ניתנת לחלוקה לשני רכיבים: ההתנגדות האמיתית של הרוטור והתנגדות נוספת . ההתנגדות הנוספת נקראת התנגדות העומס או ההתנגדות הדינמית. התנגדות העומס תלויה במהירות המנוע ואומרים שהיא מייצגת את העומס על המנוע כיוון שההספק המכני המפותח על ידי המנוע פרופורציונלי לה. במילים אחרות, התנגדות העומס היא השקולה החשמלית של עומס מכני על המנוע.

מעגל שקול של מנוע אינדוקציה במונחים של התנגדות העומס ניתן באיור 8.4. מעגל זה מוכרז כהמעגל השקול המדויק של מנוע אינדוקציה תלת-פאזי מאוזן על בסיס פר-פאזה.

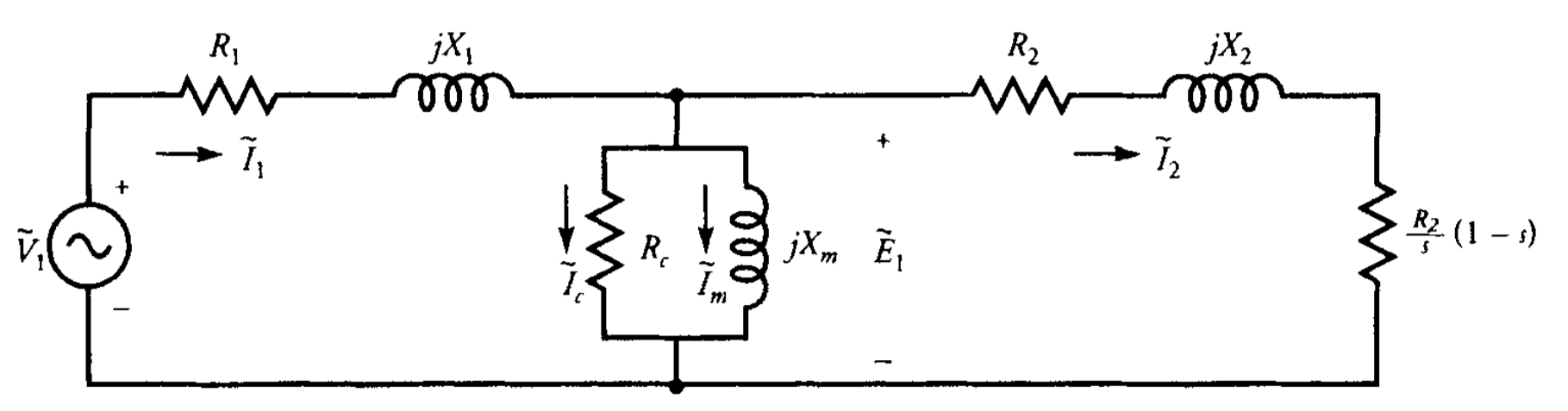
איור 8.6: המעגל השקול המדויק של מנוע אינדוקציה תלת-פאזי מאוזן על בסיס פר-פאזה במונחים של התנגדות העומס. (Guru, 2001).

יחסי הספק

מאחר שהתנגדות העומס משתנה עם ההחלקה וההחלקה מתכווננת לפי העומס המכני על המנוע, ההספק המועבר להתנגדות העומס שווה להספק המפותח על ידי המנוע. כך, ביצועי המנוע בכל החלקה ניתנים לקביעה מהמעגל השקול שלו, כפי שניתן באיור 8.4. עבור מנוע אינדוקציה תלת-פאזי מאוזן:

כאשר הוא הפרש הפאזה בין המתח המופעל וזרם ליפוף הסטטור .

מאחר שההספק הכניסה הוא חשמלי באופיו, עלינו לקחת בחשבון תחילה את ההפסדים החשמליים. ההפסד החשמלי המיידי שיש לקחת בחשבון הוא הפסד הנחושת בסטטור. סך הפסד הנחושת בסטטור הוא:

כאשר הוא עבור stator, ו- הוא עבור copper loss.
אם הפסד הליבה מדומה על ידי התנגדות אובדני ליבה שקולה, כפי שמוצג באיור, עלינו לקחת בחשבון גם את סך הפסד הליבה (הפסד מגנטי):

ההספק הנקי שחוצה את רווח האוויר ומועבר לרוטור על ידי השראה אלקטרומגנטית נקרא הספק רווח האוויר. במקרה זה, הספק רווח האוויר הוא:

הספק רווח האוויר חייב להיות שווה גם להספק המועבר להתנגדות ההיפותטית . כלומר:

ההפסד החשמלי במעגל הרוטור הוא:

לפיכך, ההספק המפותח על ידי המנוע הוא:

כאשר היא המהירות ביחידה (מנורמלת) של המנוע.

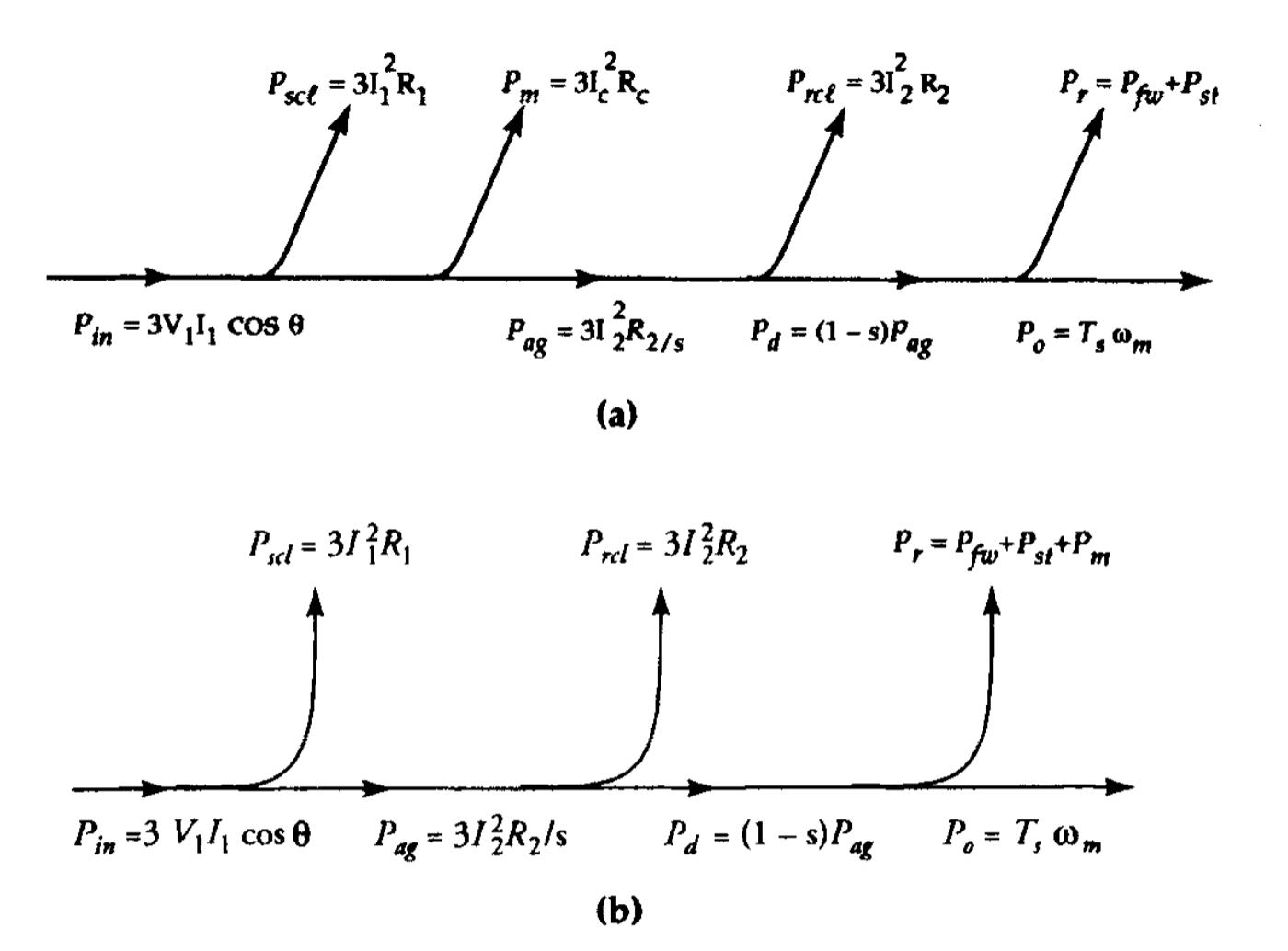
איור 8.7: דיאגרמת זרימת הספק כאשר הפסד הליבה (a) מדומה על ידי , ו-(b) מטופל כחלק מההפסד הסיבובי. (Guru, 2001).

המומנט האלקטרומגנטי המפותח על ידי המנוע הוא:

על ידי הפחתת ההפסד הסיבובי מההספק המפותח, אנו מקבלים את הספק הפלט של המנוע:

מאחר שהפסד הליבה כבר נלקח בחשבון, ההפסד הסיבובי כולל הפסד חיכוך ואוורור והפסד עומס תועה . דיאגרמת זרימת ההספק המתאימה ניתנת באיור 8.5 (a). כאשר הפסד הליבה נחשב גם חלק מההפסד הסיבובי, יש להשמיט את התנגדות הפסד הליבה באיור 8.4, ואז משוואה (GU9.13a) הופכת ל-. דיאגרמת זרימת ההספק כאשר הפסד הליבה הוא חלק מההפסד הסיבובי ניתנת באיור 8.5 (b).

אופיין מהירות-מומנט

משוואה (GU9.16) מגלה שהמומנט המפותח על ידי מנוע אינדוקציה פרופורציונלי ישירות לריבוע הזרם במעגל הרוטור ולהתנגדות ההיפותטית השקולה של הרוטור. עם זאת, שני הגדלים - זרם הרוטור וההתנגדות ההיפותטית של הרוטור - קשורים הפוך אחד לשני. לדוגמה, אם התנגדות הרוטור גדלה, אנו מצפים שהמומנט המפותח על ידי המנוע יגדל באופן ליניארי. אבל כל עלייה בהתנגדות הרוטור מלווה בירידה בזרם הרוטור עבור אותו כא”מ מושרה ברוטור. ירידה בזרם הרוטור גורמת להפחתה במומנט המפותח. האם המומנט הכולל המפותח גדל או קטן תלוי באיזה פרמטר ממלא תפקיד דומיננטי.

בואו נבחן את מאפיין המהירות-מומנט השלם של המנוע. כאשר הוא נייח, החלקת הרוטור היא יחידה וההתנגדות האפקטיבית של הרוטור היא . גודל זרם הרוטור, מאיור 8.3, הוא:

שים לב שהתנגדות ליפוף הרוטור בדרך כלל קטנה מאוד בהשוואה לריאקטנס הזליגה שלו . כלומר, .
מומנט ההתנעה המפותח על ידי המנוע הוא:

כאשר הרוטור מתחיל להסתובב, עלייה במהירותו מלווה בירידה בהחלקתו. כש- קטנה, גדלה. כל עוד קטנה מ-, הירידה בזרם הרוטור מינימלית. כך, בטווח מהירות זה, ניתן לקרב את זרם הרוטור כ:

מאחר שזרם הרוטור כמעט קבוע, המומנט המפותח על ידי המנוע גדל עם העלייה בהתנגדות האפקטיבית . לפיכך, המומנט המפותח על ידי המנוע ממשיך לגדול עם הירידה בהחלקה כל עוד להתנגדות הרוטור יש השפעה מועטה על זרם הרוטור.

כאשר ההחלקה יורדת מתחת לערך מסוים הנקרא החלקת הפריצה , ההתנגדות ההיפותטית הופכת לגורם הדומיננטי. בטווח זה, וניתן לקרב את זרם הרוטור כ:

המומנט המפותח על ידי המנוע פרופורציונלי כעת להחלקה . ככל שההחלקה קטנה, כך גם המומנט המפותח. ללא עומס, ההחלקה כמעט אפס, ההתנגדות ההיפותטית של הרוטור כמעט אינסופית, זרם הרוטור כמעט אפס, והמומנט המפותח כמעט אפס.

עם הבנה זו, אנו יכולים לשרטט את עקומת המהירות-מומנט של מנוע אינדוקציה. עקומה כזו מוצגת באיור 8.6.

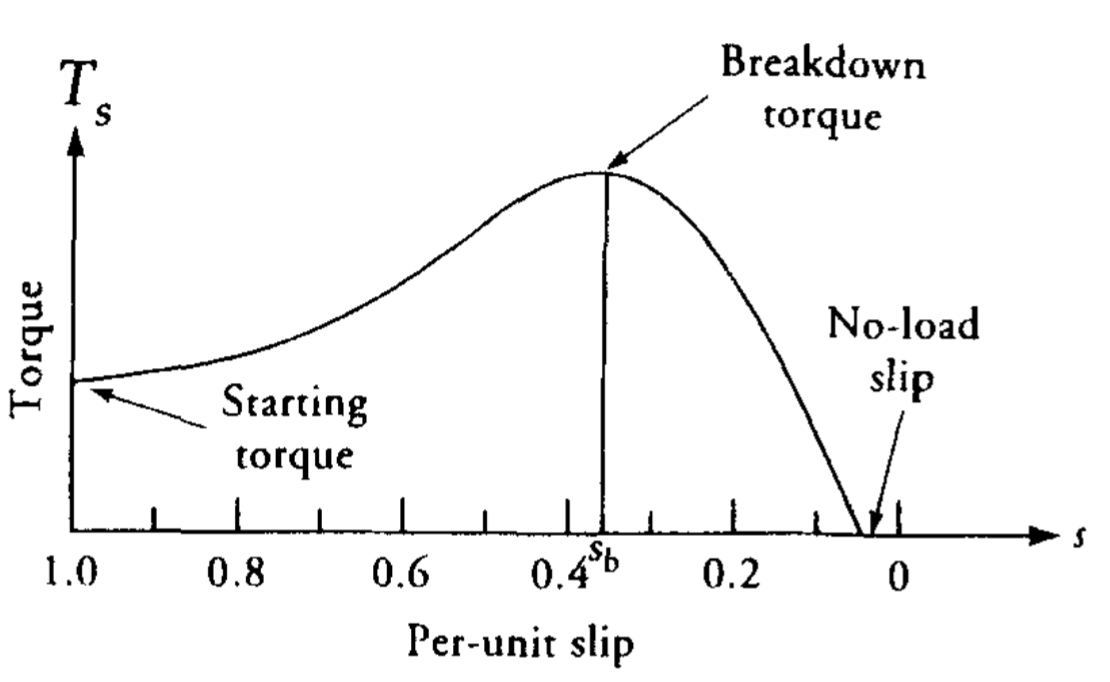
איור 8.8: מאפיין מהירות-מומנט טיפוסי של מנוע אינדוקציה תלת-פאזי. (Guru, 2001).

דוגמה:

למנוע אינדוקציה תלת-פאזי בעל 6 קטבים, , , מחובר , יש את הפרמטרים הבאים על בסיס פר-פאזה:
, , , , , ו-.
הפסד החיכוך והאוורור הוא . קבעו את היעילות של המנוע בהחלקה הנקובה שלו של .

פתרון:

המהירות הסינכרונית של המנוע היא:

המתח המופעל פר-פאזה הוא:

האימפידנס האפקטיבי של הרוטור כפי שמיוחס לסטטור היא:

אימפידנס ליפוף הסטטור היא:

מאחר ש-, , ו- במקביל, אנו יכולים לחשב את האימפידנס השקול כ:

או

לפיכך, סך האימפידנס הכניסה הוא:

זרם הסטטור:

מקדם ההספק:

הספק כניסה:

הפסד נחושת סטטור:

זרם הפסד ליבה:

זרם מגנטיזציה:

זרם עירור:

לפיכך, זרם הרוטור:

הפסד ליבה:

הספק רווח אוויר:

הפסד נחושת רוטור:

הספק מפותח:

הספק פלט:

יעילות:

מומנט גל:

מעגל שקול מקורב

מנוע אינדוקציה תלת-פאזי מתוכנן היטב עומד בדרך כלל ברוב ההנחיות הבאות:

1. התנגדות ליפוף הסטטור נשמרת קטנה כדי להפחית את הפסד הנחושת בסטטור.

2. ריאקטנס הזליגה של ליפוף הסטטור ממוזער על ידי הפחתת אורך האמצע של כל סליל.

3. למינציות דקות של פלדה דלת הפסדים משמשות לצמצום הפסד הליבה. לפיכך, התנגדות הפסד הליבה השקולה בדרך כלל גבוהה.

4. הפרמביליות של הפלדה הנבחרת ללמינציות גבוהה, וצפיפות השטף המופעלת במנוע נשמרת מתחת לברך עקומת המגנטיזציה. לפיכך, ריאקטנס המגנטיזציה בדרך כלל גבוה.

מנוע אינדוקציה העומד בדרישות לעיל ניתן לייצוג על ידי מעגל שקול מקורב, כפי שמוצג באיור 8.7. במקרה זה, הצבנו את הענף המקבילי (מעגל העירור) על פני מקור ההספק. אנו מודים שהניתוח של מנוע אינדוקציה באמצעות המעגל השקול המקורב מעט לא מדויק, אך אי הדיוק זניח עבור מנוע מתוכנן היטב. מצד שני, המעגל השקול המקורב לא רק מפשט את הניתוח אלא גם מסייע בהבנת מאפיינים שונים של המנוע. לדוגמה, אנו משתמשים במעגל השקול המקורב כדי לקבוע את המהירות שבה (א) המומנט המפותח מקסימלי, (ב) ההספק המפותח מקסימלי, ו-(ג) יעילות המנוע מקסימלית.

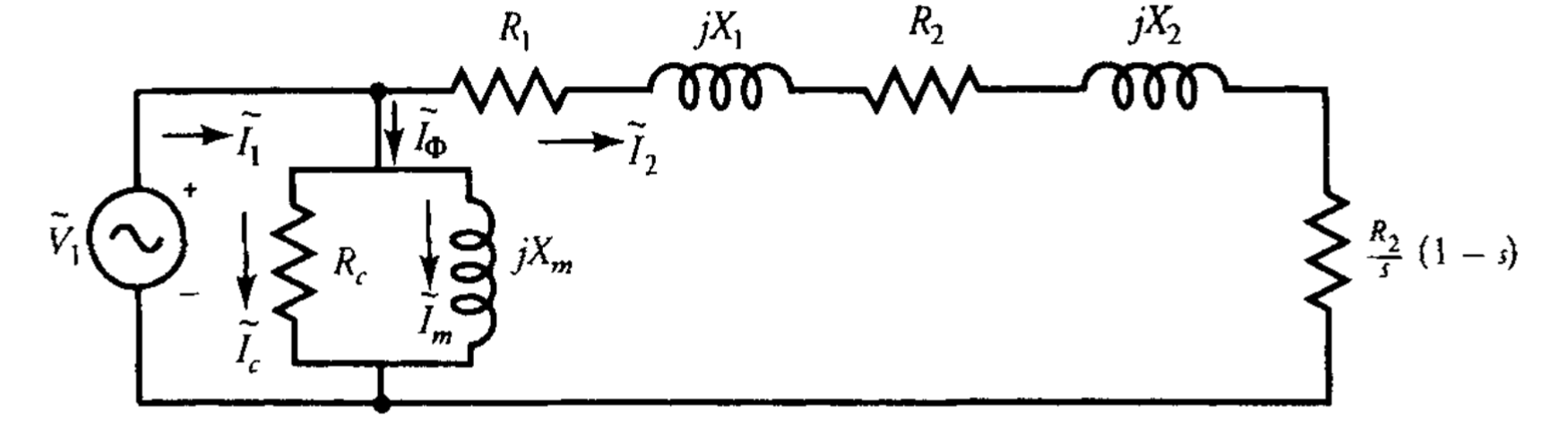
מעגל שקול מקורב על בסיס פר-פאזה של מנוע אינדוקציה תלת-פאזי מאוזן. (Guru, 2001).

לפני שנמשיך הלאה, בואו נבחן את השגיאה המוכנסת כאשר מנוע אינדוקציה מנותח באמצעות מעגל שקול מקורב.

דוגמה:

באמצעות הנתונים של הדוגמה הקודמת והמעגל השקול המקורב, קבעו את היעילות של המנוע בהחלקה הנקובה שלו של .

פתרון:

זרם הפסד ליבה:

זרם מגנטיזציה:

האימפידנס השקול של המעגל הסדרתי הוא:

לפיכך, זרם הרוטור הוא:

הזרם פר-פאזה המסופק על ידי המקור הוא:

הספק כניסה:

הפסד נחושת סטטור:

הפסד נחושת רוטור:

הפסד ליבה:

הספק פלט:

לבסוף, היעילות:

קריטריון הספק מקסימלי

מהמעגל השקול כפי שניתן באיור 8.7, זרם הרוטור הוא:

כאשר:

ההספק המפותח על ידי מנוע האינדוקציה התלת-פאזי, ממשוואה (GU9.15), הוא:

מהמשוואה לעיל ברור שההספק המפותח על ידי מנוע אינדוקציה תלת-פאזי הוא פונקציה של ההחלקה. לפיכך, ניתן לקבוע את ההחלקה שבה ההספק המפותח על ידי המנוע הוא מקסימלי על ידי גזירת המשוואה לעיל והשוואת הנגזרת לאפס. לאחר הגזירה וצמצום רוב האיברים, אנו מקבלים:

או

כאשר הוא גודל האימפידנס השקול של ליפופי הסטטור והרוטור במנוחה. כלומר:

משוואה (GU9.24) קובעת שההספק המפותח על ידי מנוע אינדוקציה תלת-פאזי הוא מקסימלי כאשר ההתנגדות השקולה של העומס (הדינמית) שווה לגודל אימפידנס העמידה של המנוע.

מתוך משוואה (GU9.24) אנו מקבלים את ההחלקה שבה מנוע האינדוקציה מפתח הספק מקסימלי כ:

בהצבת ההחלקה במשוואה (GU9.23), אנו מקבלים ביטוי להספק המקסימלי המפותח על ידי מנוע אינדוקציה תלת-פאזי כ:

כאשר הוא עבור developed ו- הוא עבור max.
הספק הפלט הנטו, עם זאת, קטן מההספק המפותח בכמות השווה להפסד הסיבובי של המנוע.

דוגמה:

למנוע אינדוקציה תלת-פאזי בעל 6 קטבים, , , מחובר , יש אימפידנס סטטור של לפאזה ואימפידנס רוטור שקול של לפאזה במנוחה. מצאו את ההספק המקסימלי המפותח על ידי המנוע ואת ההחלקה שבה זה מתרחש. מהו הערך המתאים של המומנט המפותח על ידי המנוע?

פתרון:

ממשוואה (GU9.26), ההחלקה שבה המנוע מפתח הספק מקסימלי היא:

ההספק המקסימלי המפותח על ידי המנוע הוא:

המהירות הסינכרונית של המנוע היא:

מהירות המנוע:

לפיכך, המומנט המפותח על ידי המנוע הוא:

קריטריון מומנט מקסימלי

המומנט המפותח על ידי מנוע אינדוקציה תלת-פאזי, ממשוואה (GU9.23), הוא:

כאשר:

על ידי גזירת המשוואה לעיל ביחס ל- והשוואתה לאפס, אנו מקבלים ביטוי עבור החלקת הפריצה שבה המנוע מפתח את המומנט המקסימלי (פריצה) כ:

שימו לב שהחלקת הפריצה פרופורציונלית ישירות להתנגדות הרוטור. מאחר שניתן להתאים בקלות את התנגדות הרוטור במנוע אינדוקציה רוטור מלופף באמצעות התנגדות חיצונית, אנו יכולים להשיג את המומנט המקסימלי בכל מהירות רצויה, כולל במהירות אפס (התנעה).

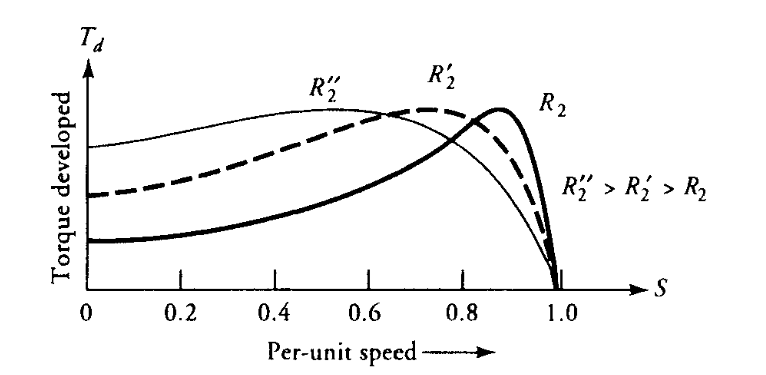
השפעת התנגדות הרוטור על החלקת הפריצה. (Guru, 2001).

על ידי הצבת הביטוי להחלקת הפריצה במשוואה (GU9.28), אנו מקבלים ביטוי למומנט המקסימלי המפותח על ידי המנוע כ:

שימו לב שהמומנט המקסימלי המפותח על ידי המנוע אינו תלוי בהתנגדות הרוטור. במילים אחרות, המנוע מפתח את אותו מומנט מקסימלי ללא קשר להתנגדות הרוטור שלו. התנגדות הרוטור משפיעה רק על החלקת הפריצה (או מהירות הפריצה) שבה המומנט הוא מקסימלי, כפי שמתואר באיור 8.8.

דוגמה:

באמצעות הנתונים של הדוגמה הקודמת, קבעו (א) את החלקת הפריצה, (ב) את מומנט הפריצה, ו-(ג) את ההספק המתאים המפותח על ידי המנוע.

פתרון:

פרמטרי המנוע הנתונים בדוגמה הקודמת הם:

החלקת הפריצה ממשוואה (GU9.29):

ממשוואה (GU9.30), מומנט הפריצה המקסימלי המפותח על ידי המנוע הוא:

ההספק המפותח על ידי המנוע בחלקת הפריצה הוא:

כאשר אנו משווים את הביטויים עבור החלקת הפריצה, משוואה (GU9.29), עם ההחלקה שבה המנוע מפתח הספק מקסימלי, משוואה (GU9.26), אנו מוצאים שהמכנה במשוואה (GU9.26) גדול יותר מזה שבמשוואה (GU9.29). במילים אחרות, המנוע מפתח הספק מקסימלי בהחלקה נמוכה יותר מזו שבה הוא מפתח מומנט מקסימלי ().

קירובים נוספים

כאשר אימפידנס הסטטור קטן כל כך שניתן להזניח אותו בהשוואה לאימפידנס הרוטור במנוחה, אנו מקבלים ביטוי שימושי מאוד עבור החלקת הפריצה, ממשוואה (GU9.29), כ:

כאשר הוא עבור breakdown (פריצה).
משוואה זו קובעת שהחלקת הפריצה היא פשוט יחס של התנגדות הרוטור לריאקטנס הרוטור. כאשר התנגדות הרוטור נעשית שווה לריאקטנס הרוטור, החלקת הפריצה היא יחידה. במקרה זה, המנוע מפתח את המומנט המקסימלי בהתנעה.

הביטוי המקורב למומנט הפריצה, משוואה (GU9.30), הופך ל:

כדי להשתמש במשוואה (GU9.32), מנוע האינדוקציה חייב לפעול בהחלקה נמוכה מאוד. למעשה, רוב מנועי האינדוקציה התלת-פאזיים פועלים מתחת להחלקה של , והיחס המקורב יכול לשמש להערכת המומנט המקסימלי המפותח על ידי המנוע.

זרם הרוטור בכל מהירות כאשר אימפידנס הסטטור מוזנח הוא:

המומנט המפותח על ידי המנוע בכל החלקה הוא:

היחס של המומנט המפותח בכל החלקה למומנט הפריצה הוא:

זהו יחס שימושי מאוד, אם כי מקורב, שניתן להשתמש בו כדי לקבוע את המומנט המפותח בכל החלקה ברגע שמומנט הפריצה והחלקת הפריצה ידועים.

דוגמה:

למנוע אינדוקציה תלת-פאזי רוטור מלופף בעל 8 קטבים, , , מחובר , יש אימפידנס סטטור זניח ואימפידנס רוטור של לפאזה במנוחה. קבעו את החלקת הפריצה ואת מומנט הפריצה. מהו מומנט ההתנעה המפותח על ידי המנוע? אם מומנט ההתנעה של המנוע צריך להיות מהמומנט המקסימלי, קבעו את ההתנגדות החיצונית שיש להוסיף בסדרה עם הרוטור.

פתרון:

מהירות המנוע:

ממשוואה (GU9.32):

ממשוואה (GU9.35), מומנט ההתנעה () במונחים של המומנט המקסימלי הוא:

מכיוון שמומנט ההתנעה הוא רק מהמומנט המקסימלי, עלינו להוסיף התנגדות למעגל הרוטור. כאשר התנגדות הרוטור גדלה, החלקת הפריצה גם גדלה. אם היא החלקת הפריצה החדשה, אז:

מכיוון ש- בהתנעה ו-, המשוואה לעיל נותנת:

או:

שני השורשים של המשוואה הריבועית לעיל הם ו-. לכן, החלקת הפריצה החדשה חייבת להיות . הערך המתאים של התנגדות הרוטור, ממשוואה (GU9.31), הוא:

לפיכך, ההתנגדות החיצונית שיש להוסיף בכל פאזה בסדרה עם התנגדות הרוטור היא .

קריטריון יעילות מקסימלית

כאשר הפסד הליבה נחשב כחלק מההפסד הסיבובי, הספק הכניסה למנוע באמצעות המעגל השקול המקורב הוא:

כאשר הוא זווית מקדם ההספק בין המתח המופעל וזרם הרוטור .

הספק הפלט הוא:

יעילות המנוע היא:

על ידי גזירת ביחס ל- והשוואת הנגזרת לאפס, אנו מקבלים:

כקריטריון ליעילות המקסימלית של מנוע אינדוקציה. זה פשוט קובע שהיעילות של מנוע אינדוקציה היא מקסימלית כאשר סכום הפסדי הנחושת של הסטטור והרוטור שווה להפסד הסיבובי.

מסקנות חשובות

לפני שנמשיך הלאה, בואו נעצור ונבצע את ההערות הבאות לגבי המומנט המפותח, זרם הרוטור ויעילות המנוע.

המומנט המפותח

כאשר המנוע פועל בהחלקה הנקובה או קרוב אליה, שהיא בדרך כלל פחות מ-, ההתנגדות ההיפותטית של הרוטור גדולה במידה ניכרת מריאקטנס הזליגה של הרוטור. כלומר, . לכן, אנו יכולים לקרב את משוואה (GU9.34) כ:

מכאן:

1. המומנט המפותח על ידי המנוע פרופורציונלי להחלקה כאשר המתח המופעל והתנגדות הרוטור נשמרים קבועים. בטווח הליניארי הזה, יחס המומנטים המפותחים שווה ליחס ההחלקות.

2. המומנט המפותח פרופורציונלי הפוך להתנגדות הרוטור בהחלקה נתונה כאשר המתח המופעל נשמר זהה. במילים אחרות, המומנט המפותח בכל החלקה ניתן להתאמה על ידי שינוי התנגדות הרוטור. זה יכול להתבצע בקלות במנוע רוטור מלופף.

3. בערך מוחלט של החלקה והתנגדות הרוטור, המומנט המפותח על ידי המנוע פרופורציונלי ישירות לריבוע המתח המופעל.

4. עבור פעולת מומנט קבוע תחת מתח מופעל קבוע, החלקת המנוע פרופורציונלית ישירות להתנגדות הרוטור.

זרם הרוטור

ממשוואה (GU9.33) ברור שזרם הרוטור פרופורציונלי ישירות למתח המופעל כל עוד התנגדות הרוטור וההחלקה נשמרים זהים. כאשר , זרם הרוטור ניתן לקירוב כ:

מכאן:

1. זרם הרוטור משתנה ליניארית עם ההחלקה כאשר המנוע פועל בהחלקה נמוכה.

2. זרם הרוטור משתנה הפוך עם התנגדות הרוטור.

יעילות המנוע

עבור מנוע אידיאלי אנו יכולים להניח ש-(א) הפסד הנחושת של הסטטור זניח ו-(ב) ההפסד הסיבובי הוא אפס. במקרה זה, הספק רווח האוויר שווה להספק הכניסה. כלומר, . עם זאת, ההספק המפותח הוא , כאשר היא המהירות ביחידה. מכיוון שההפסד הסיבובי הוא אפס, הספק הפלט שווה להספק המפותח. לכן, יעילות המנוע תחת התנאים האידיאליים היא:

המשוואה לעיל מציבה גבול מקסימלי על היעילות של מנוע אינדוקציה תלת-פאזי. משוואה זו מדגישה את העובדה שאם מנוע פועל ב- מהמהירות הסינכרונית שלו, היעילות המקסימלית תחת התנאים האידיאליים (התיאורטית האפשרית) היא . לכן, ככל שמהירות הפעולה גבוהה יותר, כך היעילות גבוהה יותר. לדוגמה, מנוע הפועל בהחלקה של יכול תיאורטית להיות בעל יעילות של .

יחסי הספק במנועי אינדוקציה תלת-פאזיים

יחסי הספק תלת-פאזיים

עבור מנוע אינדוקציה תלת-פאזי מאוזן, לפי הספק פעיל הגבי ונדמה:
הספק נדמה:

הספק פעיל:

הספק הגבי (כניסה):

קביעת מספר הקטבים

כאשר מספר הקטבים אינו נתון, ניתן להעריך אותו מהמהירות הנומינלית ותדירות הרשת:

ממשוואה (GU9.1a):

מכיוון ש- (תמיד יש החלקה), אנו מעריכים:

לאחר מכן מחשבים את ההחלקה לפי משוואה (GU9.3):

תרגילים

שאלה 1

נתון מנוע השראה תלת פאזי בעל:

• הספק נומינלי
• מתח נומינלי
• מהירות סיבוב נומינלית
• מקדם הספק נומינלי
• נצילות נומינלית

המנוע מחובר לרשת במתח הנומינלי ותדירות , חשבו:

1. הספק פעיל מדומה והגבי הנדרש להפעלת המנוע.
2. הזרם הנצרך על ידי המנוע.
3. מומנט יציאה.
4. החלקה.

פתרון:

1. חישוב הספקי הכניסה:
   הספק הכניסה הפעיל מוגדר כ:
   $$
   P_{\text{in},n} = \frac{P_n}{\eta_n} = \frac{75}{0.9} = \pu{83.3 kW} הספקנדמהלפימשוואה

S_{\text{in},n} = \frac{P_{\text{in},n}}{\cos(\theta_n)} = \frac{83.33}{0.8} = \pu{104.2 kVA}

הספקהגבילפימשוואה

Q_{\text{in},n} = \sqrt{{S_{\text{in},n}}^2 - {P_{\text{in},n}}^2} = \sqrt{104.16^2 - 83.33^2} = \pu{62.5 kVAr}

2. **חישוב הזרם:** מ[[ELM1_002 הספק פעיל, הגבי ונדמה#הספק-נדמה|יחסי הספק תלת-פאזיים]] ומשוואה $\text{(EX9.1)}$:

S_{\text{in},n} = 3V_nI_n

ולכן

I_n = \frac{S_{in,n}}{3V_n} = \frac{104.16 \times 10^3}{3 \times 230} = \pu{151 A}

חישובמומנטהפלטהמומנטהנומינליהואפשוט

T_n = \frac{P_n}{\omega_n} = \frac{60P_n}{2\pi N_n} = \frac{60 \times 75 \times 10^3}{2\pi \times 1480} = \pu{483.9 N.m}

חישובההחלקהתחילהנקבעאתמספרהקטביםמכיווןשמספרהקטביםאינונתוןנשתמשבמשוואה

P = \frac{120f}{N_s} \cong \frac{120f}{N_n} = \frac{120 \times 50}{1480} = 4.054

מכיווןשחייבלהיותמספרשלםותמידישהחלקהנבחר

P = 4

המהירותהסינכרוניתלפימשוואה

N_s = \frac{120f}{P} = \frac{120 \times 50}{4} = \pu{1500 rpm}

ההחלקהלפימשוואה

s = 1 - \frac{N_n}{N_s} = 1 - \frac{1480}{1500} = 0.013 \quad \text{ or }\quad 1.3%

## שאלה 2 נתון מנוע השראה תלת פאזי מסוג טבעות החלקה: - הספק נומינלי $P_n = \pu{60 kW}$ - מתח נומינלי $V_n = \pu{380 V}$ - מהירות סיבוב נומינלית $N_n = \pu{557 rpm}$ - זרם הרוטור הנומינלי $I_{2,n} = \pu{160 A}$ - יחס מומנט מקסימלי לנומינלי $T_{\max}/T_n = 2.9$ המנוע מחובר לרשת במתח הנומינלי ותדירות $f = \pu{50 Hz}$. העומס המחובר לציר המנוע בשילוב עם ההפסדים המכאניים ממודל על ידי:

T_{L} = \frac{20 \times 10^5}{750 + 3N}

חשבו את: 1. האופיין המכאני של המנוע על פי נוסחת קלוס. 2. התנגדות נוספת הדרושה לחיבור בטור למעגל הרוטור על מנת לאפשר התנעה. 3. מהירות הסיבוב במצב מתמיד בעת החיבור לנגד הנוסף. 4. מהירות הסיבוב במצב מתמיד בעת הורדת הנגד (מקוצר). 5. הפסדי ההספק והזרם ברוטור עבור סעיפים 3 ו-4. **פתרון:** 1. **האופיין המכאני של המנוע על פי נוסחת קלוס:** נחשב את מספר הקטבים $P$ ואת המהירות הסינכרונית. מ[[#עקרון-הפעולה|משוואה]] $\text{(GU9.1a)}$, נשתמש בהערכה:

P \approx \frac{120f}{N_n} = \frac{120 \times 50}{557} = 10.8

ולכן

P = 10

המהירותהסינכרוניתלפימשוואה

N_s = \frac{120f}{P} = \frac{120 \times 50}{10} = \pu{600 rpm}

ההחלקההנומינלית

s_n = \frac{N_s - N_n}{N_s} = \frac{600 - 557}{600} = 0.0717

נשתמשבנתוניםהנומינליםובמשוואהלחישובהחלקתהפריצה

\frac{T_n}{T_{dm}} = \frac{2s_n s_b}{s_b^2 + s_n^2}

מהיחסהנתוןנקבל

\frac{1}{2.9} = \frac{2s_n s_b}{s_b^2 + s_n^2}

פתרוןהמשוואההריבועית

s_b^2 - 2 \times 2.9 \times s_n \cdot s_b + s_n^2 = 0

s_b = s_n \times 2.9 \pm \sqrt{(2.9)^2 - 1} \times s_n = 0.0149,, 0.345

מכיווןשהחלקתהפריצהגדולהמהנומינלית

s_b = 0.345

המומנטהנומינלי

T_n = \frac{P_n}{\omega_n} = \frac{\pu{60000}}{557 \times(2\pi /60)} = \pu{1028 N.m}

המומנטהמקסימלי

T_{dm} = 2.9T_n = \pu{2981 N.m}

האופייןהמכאנילפימשוואה

\boxed{\frac{T_d}{T_{dm}} = \frac{2ss_b}{s^2 + s_b^2} = \frac{0.69s}{s^2 + 0.119}}

הנגדהנוסףהדרושלחיבורבטורלמעגלהרוטורעלמנתלאפשרהתנעהבהתנעהמומנטההתנעהשלהמנועלפימשוואה

T_{st} = T_{dm} \cdot \frac{2 \times 1 \times s_b}{1^2 + s_b^2} = 2981 \times \frac{2 \times 0.345}{1 + 0.119} = \pu{1839 N.m}

מומנטההתנעההדרושעלידימודלהעומס

T_{L} = \frac{20 \times 10^5}{750} = \pu{2667 N.m}

לכן המנוע אינו יכול להתניע. על פי [[#קריטריון-מומנט-מקסימלי|משוואה]] $\text{(GU9.31)}$:

s_b = \frac{R_2}{X_2}

אםנוסיףנגדבטורלמעגלהרוטורהחלקתהפריצההחדשהתהיה

s_{b,\text{new}} = \frac{R_2 + R_{adx}}{X_2} = s_b\left(1 + \frac{R_{adx}}{R_2}\right)

ההחלקההדרושהעלמנתלאפשרהתנעה

\begin{gathered}
T_{st} = T_{dm} \cdot \frac{2 \times 1 \times s_{b,\text{new}}}{1^2 + s_{b,\text{new}}^2} = T_{L} \[1ex]
\frac{2s_{b,new}}{1 + s_{b,\text{new}}^2} = \frac{{T}{L}}{T{dm}} \[1ex]
\frac{2s_{b,new}}{1 + s_{b,\text{new}}^2} = 0.895
\end{gathered}

פתרוןהמשוואההריבועית

s_{b,\text{new}} = \frac{T_{dm}}{T_{L}} \pm \sqrt{\left(\frac{T_{dm}}{T_{L}}\right)^2 - 1} = 0.664,, 1.506

מכיווןשההחלקהחייבתלהיותקטנהמ

s_{b,\text{new}} = 0.664

חישוב התנגדות הרוטור מהנתונים הנומינלים. מ[[#יחסי-הספק|משוואה]] $\text{(GU9.14)}$:

P_{rc\ell,n} = 3{I_{2,n}}^2R_2 = s_n \cdot T_n\omega_s

ולכן

R_2 = \frac{s_n \cdot T_n\omega_s}{3{I_{2,n}}^2} = \frac{0.0717 \times 1028 \times 62.83}{3 \times 160^2} = \pu{0.0607 \Omega}

הנגדהדרוש

\begin{gathered}
R_{adx} = R_2\left(\frac{s_{b,\text{new}}}{s_b} - 1\right) = 0.0607 \times \left(\frac{0.664}{0.345} - 1\right) \[1ex]
\boxed {
R_{adx}=\pu{0.056 \Omega}
}
\end{gathered}

מהירותהסיבובבמצבמתמידבעתהחיבורלנגדהנוסףמודלהעומסבהצבתהקשרביןמהירותלהחלקה

T_{L} = \frac{20 \times 10^5}{750 + 3N} = \frac{2 \times 10^6}{750 + 3N_s(1-s)}

במצבמתמידהמומנטהמפותחשווהלדרישתהעומסלפימשוואה

T_{dm} \cdot \frac{2ss_{b,\text{new}}}{s^2 + s_{b,\text{new}}^2} = \frac{2 \times 10^6}{750 + 3N_s(1-s)}

הצבתהנתונים

2981 \times \frac{2s \times 0.664}{s^2 + 0.441} = \frac{2 \times 10^6}{750 + 1800(1-s)}

פתרוןהמשוואהנותן

s = 0.1 \quad \text{or} \quad s = 0.99

בוחריםאתהפתרוןהפיזיקליהחלקהיציבה

s = 0.1

נקבל

\begin{gathered}
N_{\text{with resistor}} = N_s(1-s) \[1ex]
\boxed {
{N}_{\text{with resistor}}= \pu{540 rpm}
}
\end{gathered}

מהירותהסיבובבמצבמתמידבעתהורדתהנגדמקוצרבאופןדומהעם

2981 \times \frac{2s \times 0.345}{s^2 + 0.119} = \frac{2 \times 10^6}{750 + 1800(1-s)}

פתרוןהמשוואהנותן

s = 0.033 \quad \text{םר} \quad s = 0.72

בוחריםאתהפתרוןהפיזיקלי

s = 0.033

ואז

\boxed{N_{\text{without resistor}} = \pu{580 rpm}}

הפסדיההספקוהזרםברוטורעבורסעיפיםוהמומנטבעבודהבמצבמתמיד

T_d = T_{L} = \frac{20 \times 10^5}{750 + 3N}

הפסדי הנחושת ברוטור מ[[#יחסי-הספק|משוואה]] $\text{(GU9.14)}$:

P_{rc\ell} = s \cdot P_{ag} = s \cdot T_d\omega_s

הספק רווח האוויר מ[[#יחסי-הספק|משוואה]] $\text{(GU9.16)}$:

P_{ag} = T_d\omega_s = T_d \times \frac{2\pi N_s}{60}

זרם הרוטור מ[[#יחסי-הספק|משוואה]] $\text{(GU9.14)}$:

\begin{gathered}
P_{rc\ell} = 3{I_2}^2(R_2 + R_{add}) \[1ex]
I_2 = \sqrt{\frac{P_{rc\ell}}{3(R_2 + R_{add})}}
\end{gathered}

החישובים מניבים: | | **ללא נגד נוסף** | **עם נגד נוסף** | | ------------------------- | ------------ | ----------- | | $R_{adx}[\Omega]$ | $0$ | $0.056$ | | $N[\mathrm{rpm}]$ | $580$ | $540$ | | $s$ | $0.033$ | $0.1$ | | $T_d[\pu{N.m}]$ | $802$ | $844$ | | $P_{rc\ell}[\mathrm{kW}]$ | $1.66$ | $5.30$ | | $I_2[\mathrm{A}]$ | $159$ | $136$ | הוספת הנגד מגבירה את המומנט אך מגבירה גם את ההפסדים ומפחיתה את המהירות במצב מתמיד. רוטור טבעות החלקה הינו יקר יותר ובעל בלאי גבוה יותר. היום משתמשים בעיקר ב-Variable Frequency Drive (VFD) לשליטה במומנט על ידי שינוי תדירות מקור המתח. מ[[#קריטריון-מומנט-מקסימלי|משוואה]] $\text{(GU9.30)}$:

T_{dm} \sim \frac{{V_1}^2}{f}

→ קודם: ELM1_007