תרגיל בית 2

קורס	הנע חשמלי
מספר קורס	00340034

	סטודנט א’	סטודנט ב’	סטודנט ג’
שם	עידו פנג בנטוב	ניר קרל	יובל הנדל
ת”ז	CLASSIFIED	CLASSIFIED	CLASSIFIED
דואר אלקטרוני	CLASSIFIED	CLASSIFIED	CLASSIFIED

---

---

שאלה 1

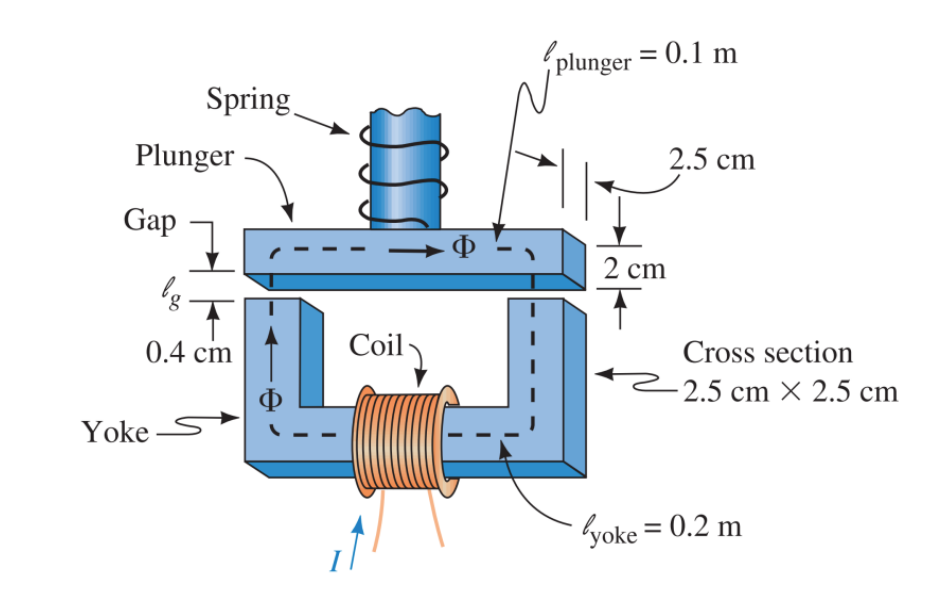
סולנואיד.

נתון:

סעיף א’

נבנה אנלוגיה חשמלית שקולה.

מעגל חשמלי שקול. הוא רילקטנס הליבה בכל צד, הוא רילקטנס כל אחד מהמרווחים ו- הוא רילקטנס החלק העליון.

מהגדרת הרילקטנס, ומסימטריה, הרילקטנס של שני המרווחים הוא:

כאשר ו- . בנוסף, הרילקטנסים האחרים:

כאשר , , ו- . לפיכך, ההתנגדות השקולה לפי חיבור נגדים בטור:

נשים לב שגם:

לפי כוח במערכת אלקטרומגנטית:

נתון כי במצב הנתון החלק העליון בשיווי משקל ולכן כאשר :

מאחר ו- , נוכל לרשום:

נעביר אגפים:

נציב ערכים ונקבל:

סעיף ב’

מאחר ואנו יודעים את , ו- (נתון ):

נשים לב שלאחר הצבת ערכים (עם ו- ) ולכן:

שאלה 2

נבנה מעגל שקול לבעיה הנתונה (לפי מנוע טורי).

מעגל שקול למנוע בעירור טורי.

נתונים:

סעיף א’

מ-KVL:

אנו יודעים מכא”מ במכונות DC ש:

נשווה בין שתי המשוואות:

ולכן:

ההספק המפותח הוא:

נציב ערכים (נשים לב ש- ונקבל:

סעיף ב’

נחשב את :

סעיף ג’

ניקח בחשבון את ההפסדים בליפופי השדה וההפסדים ברוטור:

בטור מתקיים . נציב את הערכים הידועים ונקבל:

סעיף ד’

הנצילות היא פשוט:

מאחר ואין הפסדים קבועים, מתקיים , ולכן:

סעיף ה’

נתון כי , ולכן כאשר , מתקיים . לפיכך ההספק החדש הוא:

הכא”מ הנגדי:

ולכן:

נציב ערכים ונקבל:

סעיף ו’

כבר חושב כי: