תרגיל בית 2

קורס	אלמנטים סופיים לאנליזה הנדסית
מספר קורס	00350022

	סטודנט א’
שם	עידו פנג בנטוב
ת”ז	CLASSIFIED
דואר אלקטרוני	CLASSIFIED

---

---

בעיה 1

מוט חד-ממדי עם מעבר חום.

נתונים עבור החישובים ב-MATLAB:

בעיית התנאי שפה היא:

שאלה 1

נפתור את הבעיה אנליטית; נתחיל מהעברת אגפים, כאשר נסמן :

נבצע אינטגרציה:

ועוד אחת:

נציב תנאי שפה:

נקבל:

לאחר סידור:

שאלה 2

נכפיל את (HW1.1) ב- ובפונקציית בוחן ונבצע אינטגרציה לאורך התחום:

נבצע אינטגרציה בחלקים על האינטגרל הראשון:

נציב בחזרה:

נעביר אגפים:

פונקציית הבוחן קינמטית קבילה ולכן, מאחר ויש תנאי דיריכלה ב- , מתקיים . כלומר, נישאר עם:

נציב גם את תנאי נוימן בקצה ():

שאלה 3

בהנחה ואנו מקרבים את הפתרון ע”י :

נגדיר את מטריצת הקשיחות ווקטור העומס:

ולכן נוכל לרשום את המשוואה באופן מטריצי:

נקרב את האינטגרציה ע”י פונקציות בסיס לינאריות, כאשר המיפוי שלנו לתחום האינטגרציה של אינטגרציית גאוס יהיה:

נרצה למצוא את , כלומר, את עבור אלמנט מסוים. לפי משוואה (ZT3.26):

כאשר .
לחישובים בהמשך, נצטרך לחשב עוד ערכים; היעקוביאן:

הנגזרת לפי :

נשים לב ש:

לפי (HW1.2):

נוציא מהאינטגרל ונקבל:

שאלה 4

לפי אינטגרציית גאוס על (HW1.5) עם נקודה אחת - ו-:

נקבל:

בחירת אינטגרציה בנקודה אחת היא לא הבחירה הכי נכונה כאן, אבל היא נעשה למען פישוט החישוב על הדפוס. כעיקרון, כדאי לבחור באינטגרציה בשתי נקודות כי האינטגרנד כולל פולינום ממעלה שנייה (כל הוא פולינום ממעלה ראשונה - מה שרלוונטי עבור מטריצת המסה בהמשך). בנוסף, הוא אקספוננט, אז יש לשקול אם לבצע אפילו אינטגרציה ביותר נקודות.

שאלה 5

משוואה (HW1.3):

נבצע אינטרפולציה על לפי הפונקציות בסיס (תאכלס, אנחנו יודעים ש- קבוע, אבל למען ההכללה, נתייחס לרגע כאילו הוא לא):

נציב בחזרה ונקבל:

נגדיר:

כך שנוכל לרשום:

שאלה 6

נחשב את מטריצת המסה. נפרק לאלמנטים:

בעזרת אותו המיפוי, נשים לב ש:

לפי אינטגרציית גאוס בנקודה אחת:

נקבל:

שאלה 7

עבור שני אלמנטים, , ואז:

מבחינת מטריצת המסה המקומית:

לכן המטריצות הגלובליות:

נציב במערכת המשוואות:

נציב:

נציב את תנאי דיריכלה :

נוכל כעת “להתעלם” מהשורה והעמודה הראשונה:

פתרון מערכת משוואות זו תיתן לנו את ו-.

שאלה 8, 9, 10

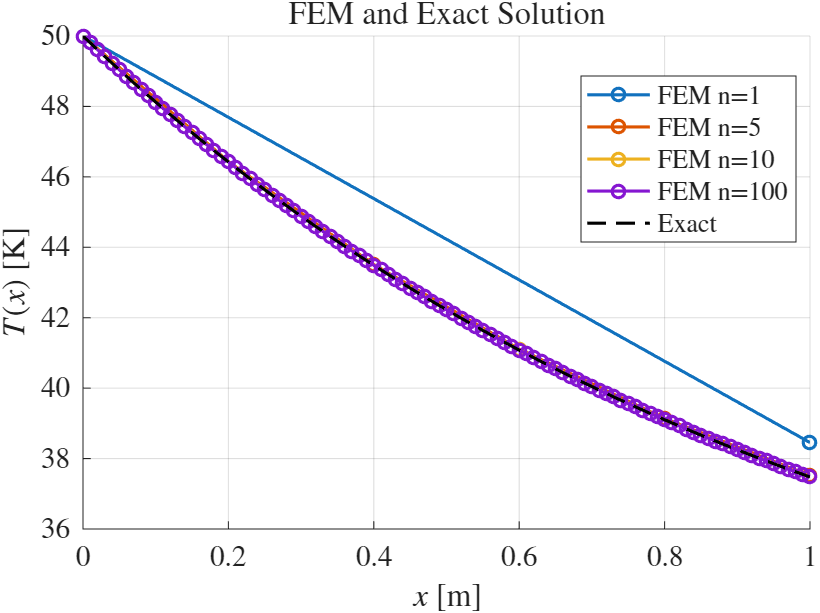
השוואה בין פתרון אנליטי (מדויק) לפתרון נומרי בשיטת האלמנטים הסופיים.

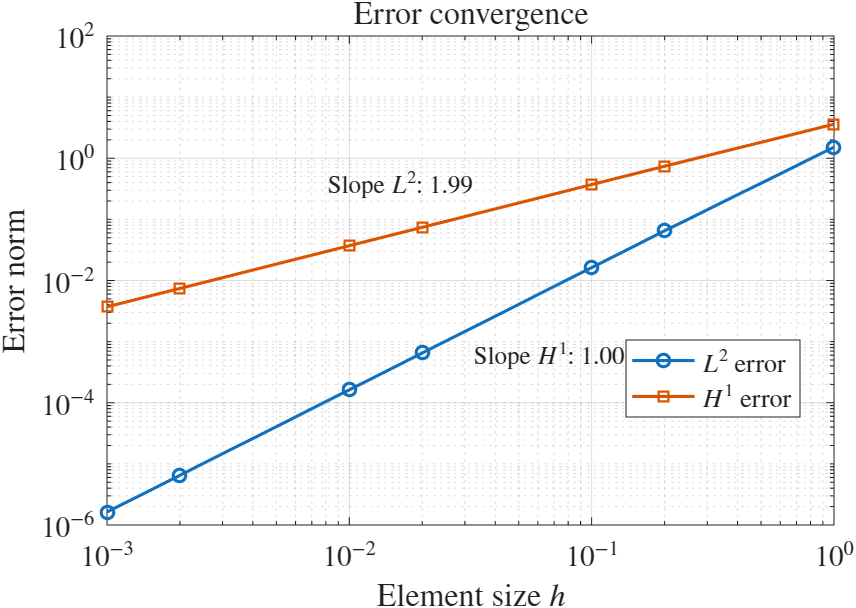
התכנסות השגיאה ( ו-) של פתרון האלמנטים הסופיים כפונקציה של גודל האלמנט .