מבוא
שיטות קלאסיות לפתרון בשיטת גלרקין בונות קירובים מפונקציות קבילות קינמטית (kinematically admissible functions), שהן פונקציות שמקיימות את תנאי השפה על הזזה (דהיינו תנאי דיריכלה) מלכתחילה. שתי בעיות מרכזיות עולות:
- לפעמים זה די קשה למצוא פונקציות קבילות קינמטית בכל המרחב הרלוונטי.
- אם כן מצאנו פונקציות כאלה, הן מובילות למערכת משוואות מצומדות ומסובכות.
ניתן להתעלות על בעיות מסוג זה בעזרת העובדה שקירובים מקומיים יכולים לספק פתרונות בדיוק גבוה, ובאותו הזמן להוביל למערכת משוואות שיש להן מבנים מתמטיים נוחים לחישוב, גם בממדים גבוהים. קירובים חלקיים אלו, או “אלמנטיים” אלו, כבר הוכרו לפני לפחות 60 שנה ע”י קורנט (Courant). היה מגוון של שיטות קירוב דומות לפתרון משוואות פיזיקליות. הכי נפוצה ביניהן היא שיטת האלמנטים הסופיים, FEM. המאפיין המרכזי של שיטה זו היא חילוק המרחב באופן שיטתי להרכבה של תת-תחומים בדידים, או, “אלמנטים”, ואז לקרב את הפתרון של כל אחד מחלקים אלו באופן שמצמד אותם כדי ליצור פתרון גלובלי תקף לאורך כל התחום. התהליך פותח באופן כזה שהמשוואות האלגבריות יהיו ניתנות לחישוב (במחשב), ויעילות מבחינת הזיכרון שהן משתמשות בו.
קירוב אלמנט סופי
נביט בצורה החלשה של הבעיה שראינו בפרק קודם (משוואה (ZT2.13)):
עלינו למצוא
אנו מקרבים את
כאשר הסימון את
אם נבחר
אז אנו יכולים לרשום:
מאחר וה-
כאשר:
את (ZT3.5) אנו יכולים גם לרשום בצורה מטריציונית:
כאשר
הערה:
בתרגול אנו מפרקים את וקטור העומס
למטריצת המסה (mass matrix) ווקטור הכוח (force vector). אנו עושים זאת על קירוב בעזרת אותם הפונקציות בסיס: לכן במקרה שבו תנאי השפה נוימן הוא הומוגני, אנו מקבלים:
ל-
אנו קוראים וקטור הכוח (force vector) ולאינטגרל אנו קוראים מטריצת המסה (mass matrix).
פירוק זה עשוי להיות יקר חישובית בבעיות סטטיות, אך בבעיות דינמיות הוא מתבצע באופן טבעי מתוך פיתוח המשוואות.
בניית פונקציות בסיס של FEM
שיטת אלמנטים סופיים מגדירה פונקציות בסיס (למטרת הקירוב) באופן מקוטע (piecewise) לאורך תת-תחום, ה”אלמנטים הסופיים”, של כלל התחום. פונקציות הבסיס הן לרוב פולינומים פשוטים מסדר נמוך. אנו מקפידים שמתקיים:
- פונקציות הבסיס חלקות מספיק כך שהן חלק מ-
- פונקציות הבסיס הן פולינומים פשוטים למקוטעין, המוגדרות אלמנט-אלמנט.
- פונקציות הבסיס יוצרות בסיס בו
קבוצה של פונקציות אפשריות לבסיס מוגדרות כ:
כאשר
אחרת,
וגם
הפונקציות מסודרות כך שה-”פסגה” של הפונקציה ה-
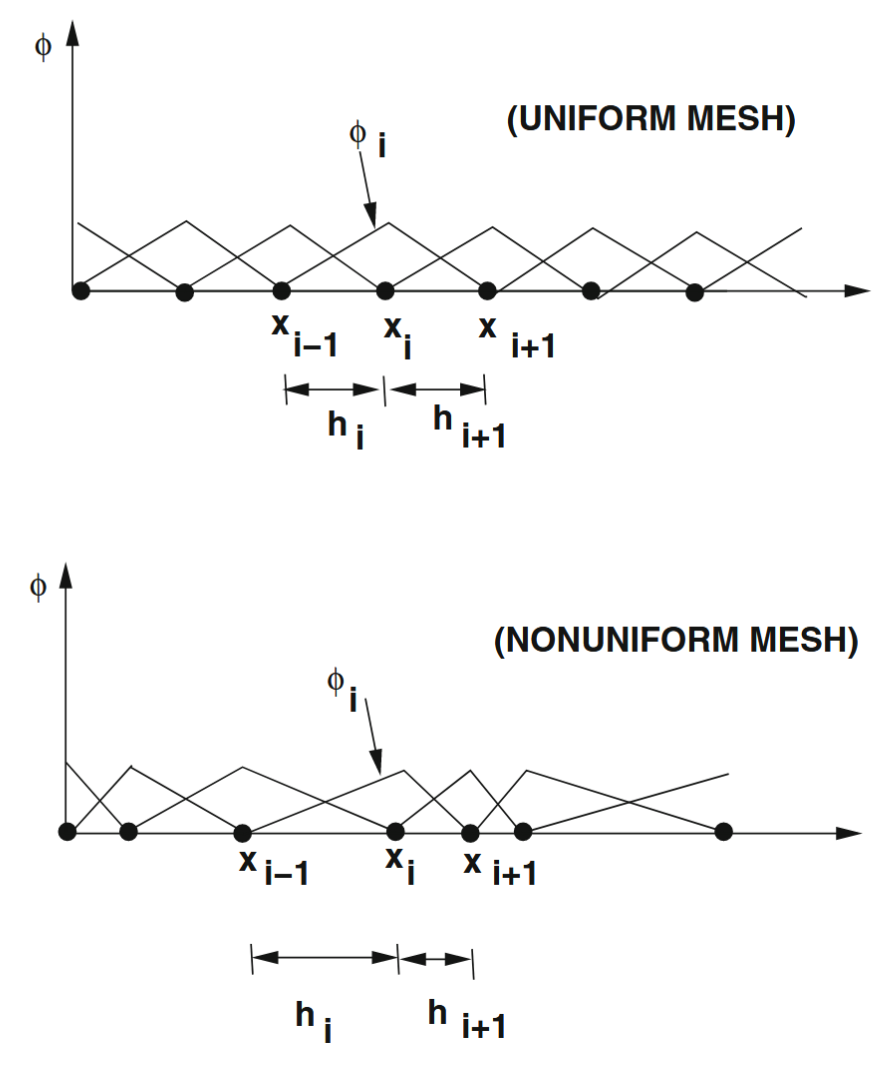
בסיס לאלמנט סופי חד-ממדי. למעלה, דוגמה לרשת אחידה. למטה, דוגמה לרשת לא אחידה. (Zohdi, 2018).
הערה:
- התחום
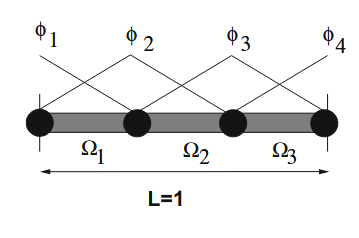
ל- הוא מה שאנו קוראים לו אלמנט סופי (finite element). - אם אנו מחלקים את התחום ל-
אלמנטים, ולכל אלמנט אנו מבצעים קירוב לינארי (linear approximation), אז יש לנו צמתים (nodes) לאורך התחום.
אינטגרציית גאוס
נחזור טיפה על אינטגרציית גאוס. גאוס שם לב שניתן לבצע אינטגרציה על פולינום מסדר
כאשר
- עבור סדר שלישי
- עבור סדר שני
- עבור ביטוי לינארי
- עבור קבוע (
אינטגרציית גאוס. (Zohdi, 2018).
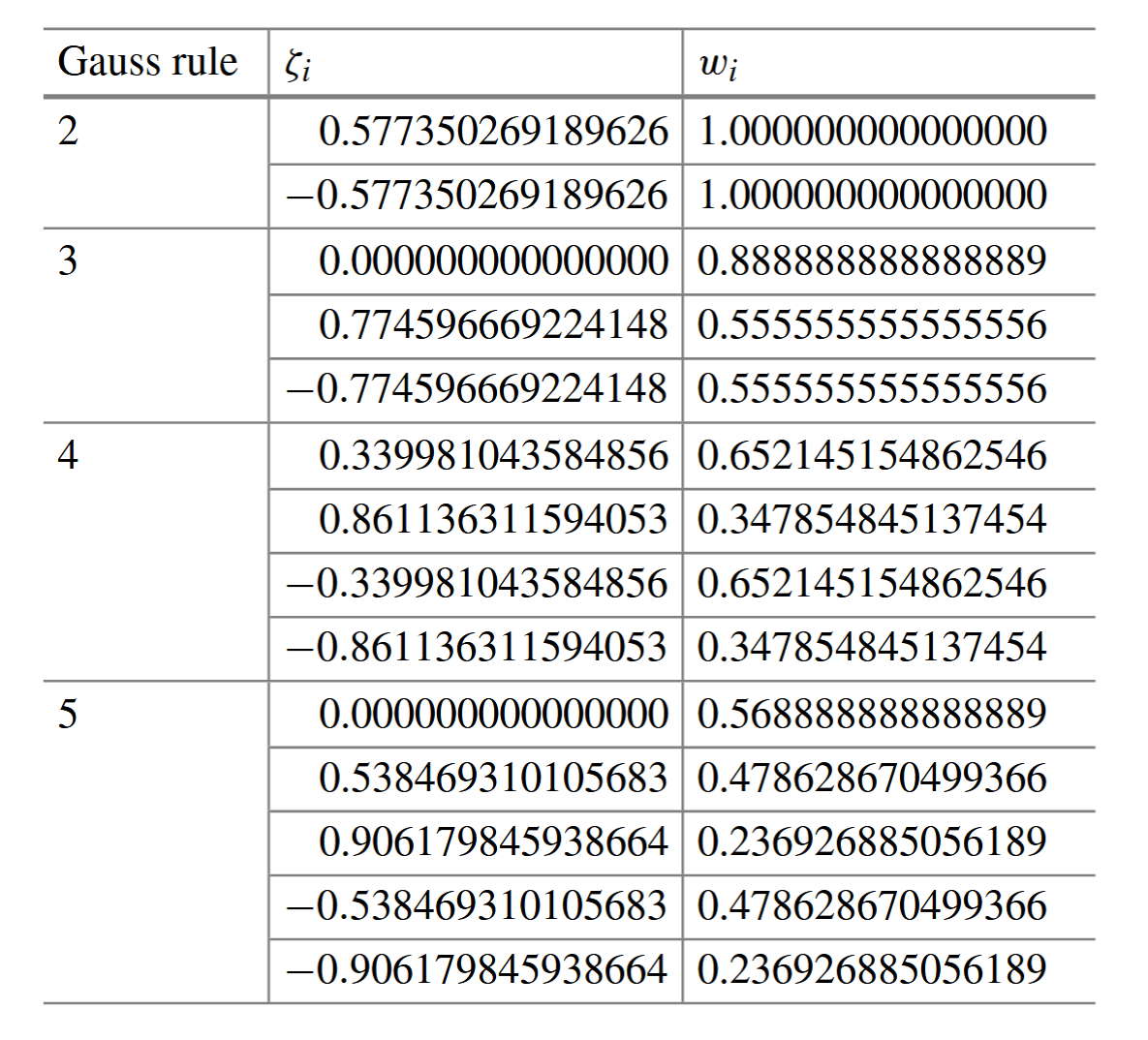
טבלה לאינטגרציית גאוס. (Zohdi, 2018).
דוגמה:
נביט באינטגרל הבא:
האינטגרל הוא מהצורה:
עם הטרנספורמציה
כאשר נבצע את טרנספורמציה זו נקבל
כאשר
. באינטגרציה בשלוש נקודות, נקבל (הפתרון המדויק הוא ):
טרנספורמציה גלובלית/מקומית
אחד מהיתרונות של שיטת אלמנטים סופיים הוא שהחישוב ניתן לביצוע אלמנט-אלמנט. את מטריצת הקשיחות
ופונקציית העומס:
אנו מחלקים את התחום
וגם:
כאשר
דוגמה:
כדי לבצע את החישובים באופן שיטתי, אנו רוצים להמיר את הקואורדינטות של כל אלמנט לתחום
כאשר
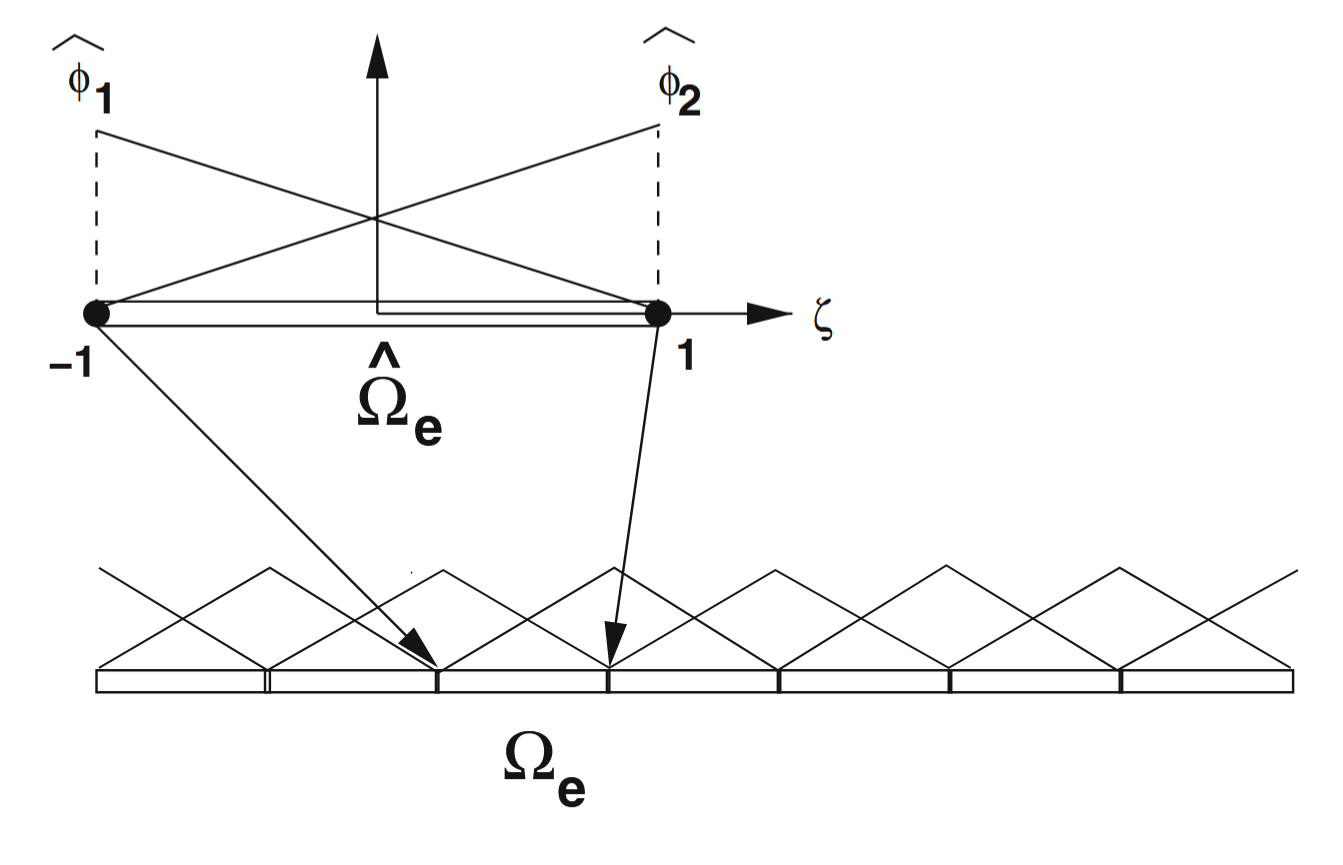
טרנספורמציה לאלמנט סופי חד-ממדי. (Zohdi, 2018).
שיטות מיפוי אלו (הטרנספורמציות) לרוב נקראים מפות “פרמטריות”. אם סדר הפולינום של פונקציות הצורה גבוהות כמו קירוב גלרקין על האלמנט, הוא נקרא מפה איזו-פרמטרית. אם הוא נמוך יותר, אז סאב-פרמטרי, ואם הוא גבוה יותר אז הוא נקרא סופר-פרמטרי.
מאפיינים דיפרנציאליים של פונקציות צורה
לקירוב לינארי, פונקציות הצורה המקומיות הן מהצורה:
יש להם את התכונות הבאות:
- לאלמנטים לינאריים יש לנו בסיס הכולל שני צמתים, ולכן שתי דרגות חופש.
- פונקציות הצורה (
הערה:
אנו לא באמת מחשבים את הפונקציות
; אנחנו למעשה מתחילים מ- ואז ממפים (transform) אותם לתחום של הבעיה האמיתית. לכן במטריצת הקשיחות או במטריצת המסה שנראה בהמשך, כל הביטויים חייבים להיות מוגדרים במונחים של קואורדינטות מקומיות (local coordinates).
כעת נגדיר מספר ביטויים בסיסיים שיעזרו לנו בחישוב הערכים המקומיים כמו
ונשים לב גם ש:
כעת נוכל לפתח ביטוי לנגזרת של
נציב ב-(ZT3.24), ונקבל בעזרת אינטגרציית גאוס:
וגם:
דוגמה:
פיתוח הצורה החלשה:
נתונה הבעיה הבאה:צורתה החלשה היא (לאחר אינטגרציה בחלקים):
נפרק את התחום לשלושה אלמנטים, ולכן נקבל ארבעה צמתים:
על אלמנט
, מתקיים ו- וגם: על אלמנט
, מתקיים ו- וגם: על אלמנט
, מתקיים ו- וגם: אנו מבצעים את החישובים אלמנט-אלמנט. כל החישובים ב-
שייכים לאלמנט , בעוד כל החישובים ב- שייכים לאלמנט , וכל החישובים ב- שייכים לאלמנט .
בניית המערכת הדיסקרטית:
עבור אלמנט, כדי לחשב את , נביט בביטוי הבא עבור ערכי : ספציפית עבור
, הביטוי הוא: כאשר אנו מקבלים המון ביטויים (כמו השלישי) שמתאפסים כי פונקציות הבסיס שם הן
בתחום האלמנט הראשון. הביטויים כמו מכפילים את הביטויים , המגדירים את המיקום שלהם בתוך מטריצת הקשיחות הגלובלית. אם נחזור על הפעולה עבור עם , נקבל את הערכים הבאים בתוך מטריצת הקשיחות הגלובלית (שהיא מטריצה מסדר כי יש צמתים): כלומר, מטריצת הקשיחות המקומית היא רק:
באותו אופן, וקטור העומס המקומי של אלמנט
הוא כך שבאופן וקטורי:
נחזור על תהליך זה על כל שלושת האלמנטים ונקבל את מטריצת הקשיחות ווקטור העומס הגלובליים:
נשים לב שבאלמנט האחרון יש לנו גם תנאי שפה שאנו חייבים להתייחס אליו בוקטור העומס:
כמובן שאת כל האינטגרלים נחשב בעזרת אינטגרציית גאוס - כלומר, נשתמש ב- (ZT3.32) ו-(ZT3.33).
אלמנטים ממעלה גבוהה
בהמון מקרים, אם אנו יודעים שהפתרון האמיתי הוא חלק, נעדיף לבצע קירוב ממעלה גבוה יותר. בכללי, אם הפתרון המדויק לבעיה הוא חלק, עבור רשת סבוכה מספיק (

שלושה אלמנטים ממעלה גבוהה עם
צמתים. (Zohdi, 2018).
כדי לבנות קירוב ממעלה שנייה לכל אלמנט, אנו נצטרך כעת
- לצומת
- לצומת
- לצומת
הקשר בין
בנוסף, למערכת המשוואות שנבנית מפונקציות אלו עדיין יש את הצורה הלינארית:
כאשר
עבור אלמנט
מה שנותן:
בצד ימין של (ZT3.51), עבור
ולכן
נחזור זאת על
נחזור זאת על אלמנטים
תרגילים
שאלה 1
הביטו במוט חד-ממדי תחת הכוח המפורש (הצירי)
סכמת הבעיה.
סעיף א’
רשמו את המשוואות השולטות בבעיה.
פתרון:
לפי משוואה (ZT2.14), או לפי משוואות תנועה של מוט במתיחה:
סעיף ב’
הגדירו את השאריות על התחום ועל תנאי השפה נוימן.
פתרון:
נסמן את הפתרון המשוער ב-
בנוימן:
סעיף ג’
מצאו את הצורה החלשה של הבעיה.
פתרון:
לפי שיטת גלרקין על המשוואה ועל התנאי שפה:
נרשום את הצורה החלשה (אינטגרציה בחלקים):
נפתח את הביטוי השני כדי לראות שיש ביטויים שמתבטלים:
התנאי שפה ב-
תנאי שפה נוימן הומוגניים תמיד מבטלים אחד את השני בצורה החלשה. לכן קוראים להם לפעמים תנאי שפה טבעיים, והם מתקיימים באופן טבעי. לפיכך, אם למשל אנו לא דורשים תנאי שפה דיריכלה מסוימים, אז זה כאילו אנחנו מניחים תנאי שפה נוימן.
תנאי השפה ב-
נישאר עם:
נשים לב שבצד שמאל מופיע מטריצת הקשיחות ובצד ימין וקטור העומס, כמו במשוואה (ZT3.5b).
נרצה כעת לדון בפונקציות הקירוב/בסיס. כאן
כאשר
האינטגרל שקיבלנו נקרא מטריצת המסה. נציב בחזרה ב-(E2.1):
כאשר
כאשר
סעיף ד’
בחרו פונקציות בסיס לשיטת אלמנטים סופיים.
פתרון:
נבחר בפונקציות בסיס שהן רציפות למקוטעין כפי שמוסבר בבניית פונקציות בסיס של FEM:
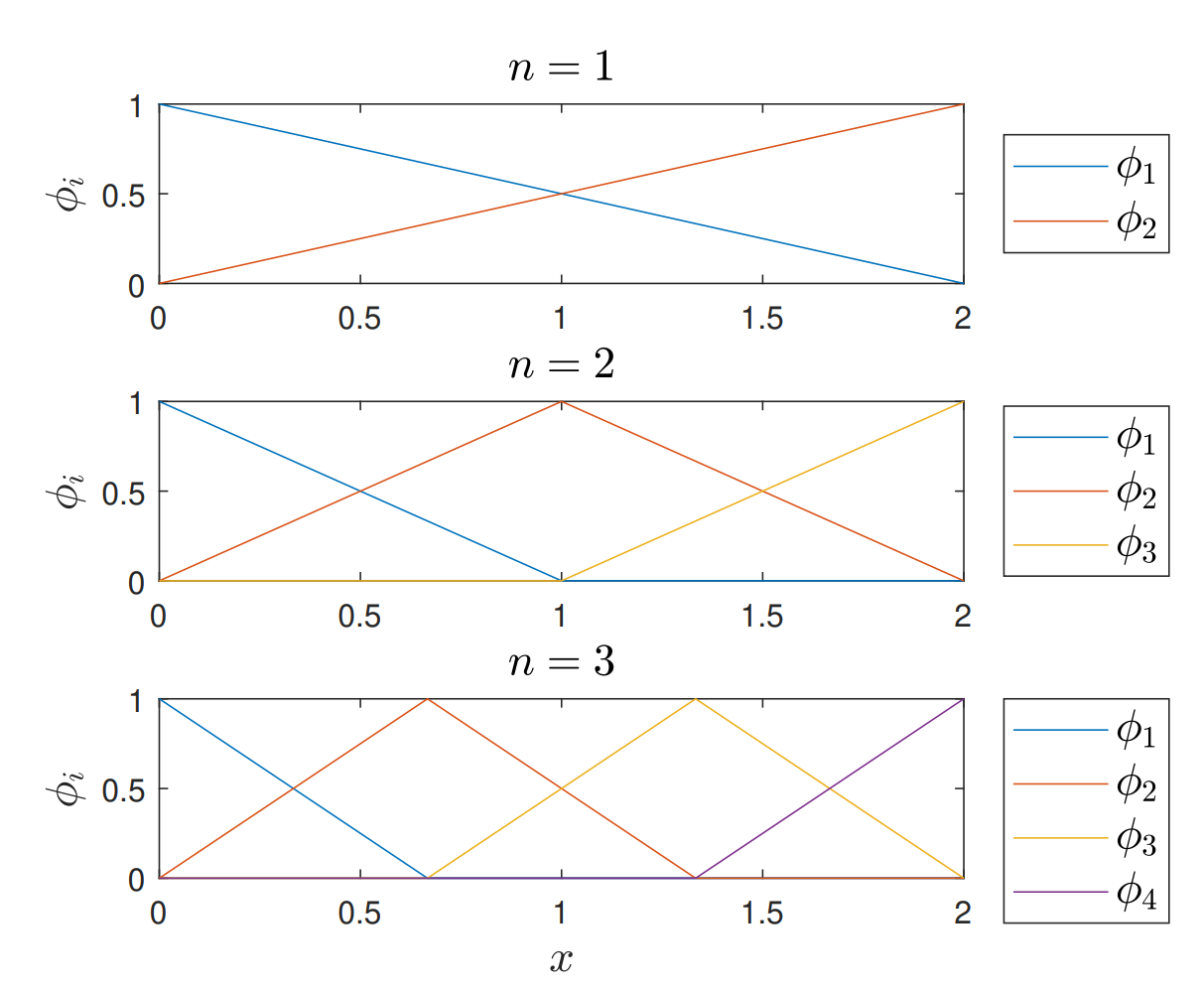
פונקציות הבסיס שאנו בוחרים בשאלה.
למשל עבור
זהו פיתוח גלובלי, כדי לפתח באופן כללי נבחן עבור אלמנט כללי - כלומר באופן מקומי.
סעיף ה’
פתחו את הטרנספורמציה/מיפוי למערכת קואורדינטות מקומיות.
פתרון:
בעצם מה שאנחנו עושים זה לקחת כל אלמנט ולבצע עליו טרנספורמציה:
טרנספורמציה מקומית של אלמנט.
במקרה שלנו:
נרצה למצוא את
כאשר
לחישובים בהמשך, נצטרך לחשב עוד ערכים; היעקוביאן:
כאשר אנו קוראים את
נסמן את הנגזרת לפי
הנגזרת לפי
סעיף ו’
מצאו את הקשיחות ה-מקומית ומטריצת המסה ה-מקומית של כל אלמנט.
פתרון:
לפי משוואות (ZT3.32):
ולכן:
מטריצת המסה:
לכן:
נבחר לחלק ל-
על כל אחד מהם אנו יכולים לבצע אינטגרציית גאוס עם נקודה אחת (האינטגרנד לינארי) עם
לכן המטריצות המקומיות (נציב
סעיף ז’
פתחו ביטוי לקשיחות ה-גלובלית ומטריצת המסה ה-גלובלית.
פתרון:
חילקנו ל-
סעיף ח’
מצאו את הקירוב לפתרון בשיטת אלמנטים סופיים.
פתרון
מבחינת וקטור הכוח, הוא פשוט
נתחיל לחשב:
כאן אנחנו כבר צריכים להיזהר ולזכור שיש לנו תנאי שפה מסוג דיריכלה ב-
לפיכך, נישאר עם מערכת המשוואות המצומצמת:
נקבל ש-:
כעת אנו יודעים את הערכים של הפתרון בצמתים, ונוכל לבצע אינטרפולציה כדי לקבל את הפתרון המקורב. נשים לב שלפי סעיף ד’:
ולכן הקירוב:
נציב ערכים ונקבל:
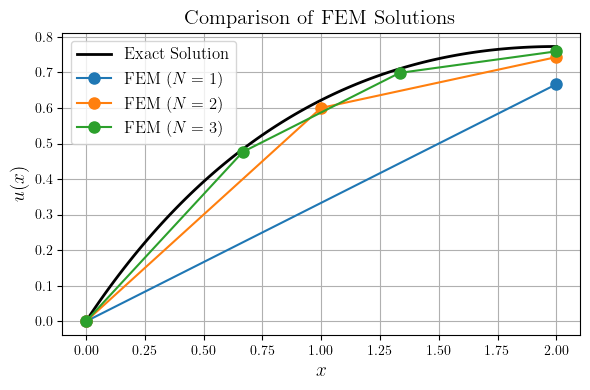
פתרון מדויק ופתרונות בשיטת אלמנטים סופיים עם מספר אלמנטים שונים.
שאלה 2
הביטו בצלע קירור הבאה:
צלע קירור הנתונה להסעה ושטף חום.
סעיף א’
רשמו את משוואות החום השולטות בצלע.
פתרון:
חתך דיפרנציאלי על הצלע.
בהנחה והשטף הנכנס הוא חיובי, שטף היציאה הוא שלילי. נרשום את מאזן החום:
לפי חוק פורייה, מתקיים
מבחינת תנאי שפה, יש לנו שטף חום מצד שמאל:
מצד ימין יש גם שטף חום וגם הסעה:
לפי פורייה בקצה, זה גם:
ננרמל כי למה לא:
נקבל את הבעיה הבאה:
סעיף ב’
הגדירו את השאריות של המשוואה ושל תנאי השפה.
פתרון:
נניח שהפתרון המקורב הוא מהצורה
השאריות של תנאי השפה:
סעיף ג’
הפעילו את שיטת גלרקין ומצאו את הנוסח החלש.
פתרון:
מעכשיו נרשום
לפי שיטת גלרקין:
לאחר אינטגרציה בחלקים נקבל את הנוסח החלש (וחלק מהאיברים יצטמצמו):
ניתן לרשום את ביטוי זה באופן מטריצה הבא:
כאשר:
סעיף ד’
מצאו ביטויים כלליים לאברי המטריצות והוקטורים המקומיים.
פתרון:
נבחר פונקציות בסיס לינאריות מקומיות:
נסמן:
לפי משוואה (ZT3.26):
בנוסף:
לגבי
סעיף ה’
פתרו את הבעיה עבור שני אלמנטים.
פתרון:
עבור שני אלמנטים מתקיים
בהנחה ו-
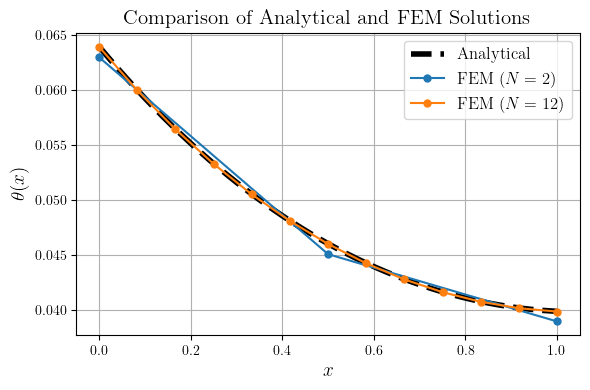
פתרון מדויק ופתרונות בשיטת אלמנטים סופיים עם מספר אלמנטים שונה.