FLD1_E2021WB 2021 חורף מועד ב'

שאלה 1

זהה לשאלה ממבחן.

שאלה 2

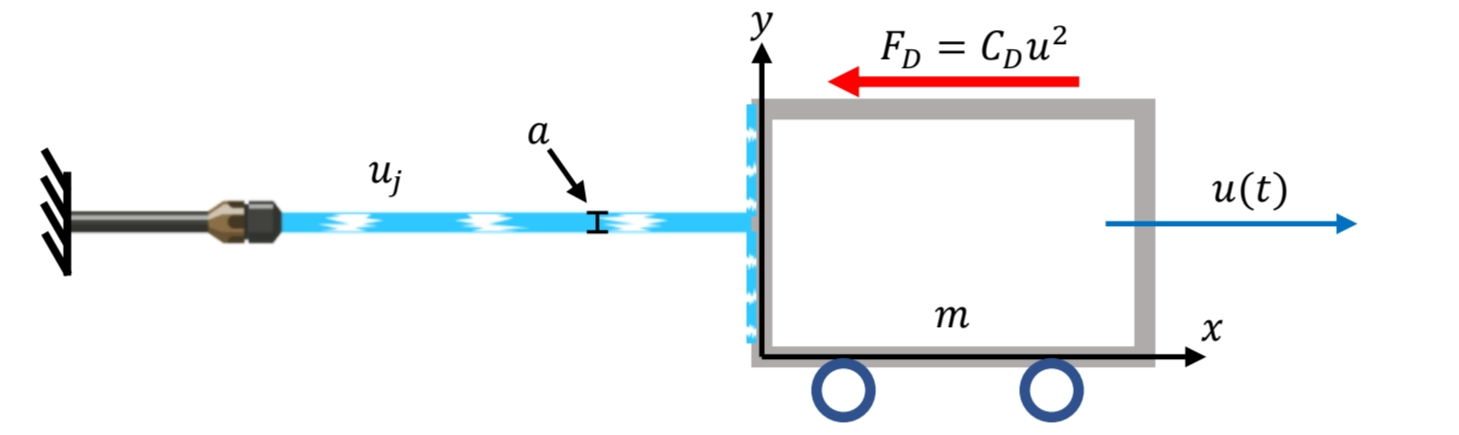
סכמת העגלה

סעיף א’

נמצא את הכוחות הפועלים על העגלה:

דג”ח על העגלה, מערכת צירים קבועה. נתייחס רק לכוחות האופקיים. הוא הכוח שהנוזל מפעיל על העגלה.

מהדג”ח וחוק שני של ניוטון, נסיק כי שתאוצת העגלה היא:

הערה:

נסמן את הוא שטח החתך של הזרם (בשונה מהסימון בשרטוט, כדי לא לבלבל עם התאוצה ).

כדי למצוא את , נבצע שימור תנע אינטגרלי. נבחר נפח בקרה על הזרם הנכנס ושפוגע בעגלה, כאשר נניח שהזרם מתפצל לזרמים בניצב לזרם הנכנס. בנוסף, נניח שלזרם פרופיל מהירות אחיד.

בחירת נפח הבקרה. נשים לב שמאחר והעגלה זזה, נפח הבקרה זז ביחד איתו.

נפח הבקרה שבחרנו והמהירות קבועה, כך שצד שמאל מתאפס. בנוסף, מייצג את הכוחות שפועלים על הזורם, ומחוק שלישי של ניוטון, זה שהגדרנו בדג”ח על המוצק. נישאר עם:

נסיק מסימטריה שאין תנע בכיוון , כך שבצד ימין נישאר רק עם הזרם בכניסה, שהוא בכיוון :

מהירות הזורם ביחס למערכת הצירים הקבועה היא , ביחס לנפח הבקרה היא , והנורמל לנפח הבקרה בכניסה הוא . נציב:

נציב בחזרה חוק השני של ניוטון עבור המוצק (העגלה):

עכשיו קלטתי שהם הגדירו את פעמיים, פעם בשרטוט ופעם במלל, בעזרת שתי הגדרות שונות. גם קלטתי מהפתרון הרשמי שאמיר ממש אבל ממש אוהב מערכות צירים לא אינרציאליות. אז נזרום עם תובנות אלו, ונרשום את הפתרון שלנו מחדש:

סעיף ב’

במצב מתמיד, . נציב בפתרון של הסעיף הקודם (במערכת צירים הלא אינרציאלית):

נפתור בעזרת נוסחת השורשים:

פיזיקלית, לא יכל להיות שמהירות העגלה גדולה יותר ממהירות הזרם, ולכן . לכן:

סעיף ג’

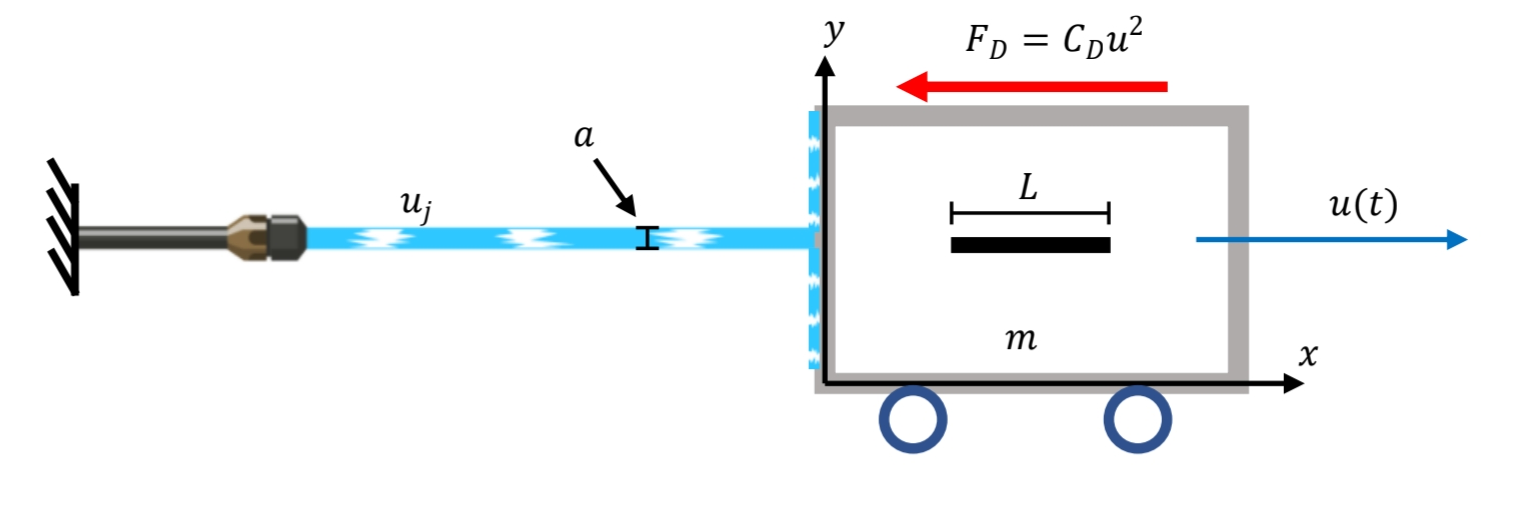
לפי בלסיוס, מאמץ הגזירה על הכנף נתון ע”י:

כוח הגרר יהיה סכימה של מאמץ זה לאורך שתי הכנפיים, מלמעלה ומלמטה:

ולכן:

סעיף ד’

בדומה לסעיף ב’, רק הפעם נתייחס גם ל-:

נדרוש :

שאלה 3

סכימת הצינור

סעיף א’

נניח כי:

1. הבעיה אקסיסימטרית - .
2. מצב מתמיד - .
3. כבידה זניחה.

ננרמל את המשוואות לפי:

נסמן גם , כך שבעצם נוכל לנרמל את האורכים לפי:

ממשוואת הרצף:

נציב את ערכי הנרמול:

מאחר ו- ו- בערך מסדר גודל , נסיק כי גם המקדמים בערך מאותו הסדר גודל:

ממשוואות נאוויה-סטוקס בכיוון הארוך:

נשים לב ש- , כך שנישאר עם:

נציב את ערכי הנרמול:

נציב גם :

נחלק ב- :

נוכל לסדר טיפה את החלק של הצמיגות:

מאחר ו- נוכל להזניח את מה שמוכפל ב- :

סעיף ב’

לפי סעיף קודם, נשים לב מצאנו ביטוי לריינולדס המוקטן במערכת הנתונה:

כאשר , נשים לב שכל הביטויים עם האינרציה במשוואה המנורמלת נופלים, כך שנישאר רק עם:

כדי לתאר את הבעיה הנתונה, אנו יודעים שפיזיקלית גם הצמיגות, גם הלחץ, וגם כוח הגוף משחקים תפקיד דומיננטי בזורם, כך שנוכל להניח שהמקדמים שלהם מאותו הסדר גודל:

מהשוואת הביטוי הראשון והשלישי:

מהשוואת הביטוי השני והשלישי:

סעיף ג’

אם נציב את הגדלים האופיינים שמצאנו בחזרה במשוואה שקיבלנו בסעיף א’ נקבל:

ולכן המשוואה הלא מנרומלת היא (נשים לב להחזיר את כל הגדלים שלא נרמלנו, בינהם ):

נניח שהזרימה מפותחת, כך שמתקיים . לכן, צד ימין של המשוואה שקיבלנו תלויה רק ב-, וצד שמאל תלוי רק ב- (נניח גם ש- , נובע ממשוואת נאוויה-סטוקס בכיוון ), כך ששני הביטויים שווים לקבוע:

נתחיל מהביטוי השמאלי - נבצע עליו אינטגרציה לפי :

נציב תנאי שפה:

ולכן פילוג הלחץ הוא:

סעיף ד’

מסעיף קודם:

תנאי השפה שלנו הם תנאי אי-חדירה ותנאי אי-החלקה על דפנות הצינור- נקבל פרופיל זרימת האגן-פואזיי:

נציב את מסעיף קודם ונקבל:

פרופיל המהירות והלחץ - ניתן לשנות את .

שאלה 4

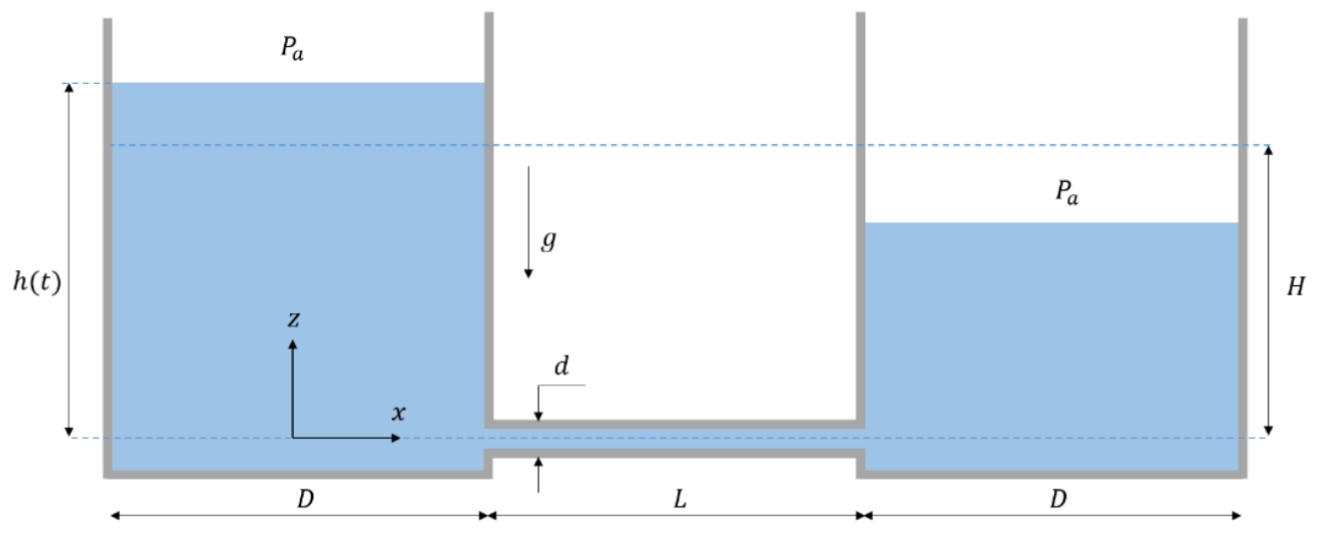
סכימת המיכלים

סעיף א’

נבצע שימור מסה אינטגרלי. נבחר נפח בקרה משתנה עם הזמן שגבולותיו הם המיכל והפתח לצינור, כאשר הגובה שלנו נקבע לפי גובה מפלס הזורם.

בחירת הנפח בקרה ומערכת הצירים.

מאחר ו- קבוע לאורך כל הנפח הבקרה, נוכל לחלק בו כדי לקבל:

נוכל להזניח את נפח הפתח לצינור, כך שהנפח של נפח הבקרה הוא:

כאשר הוא שטח המיכל. נסיק ש- .
בנוסף, הפתח היחיד לנפח הבקרה הוא לצינור (מחלקו העליון של נפח הבקרה לא נכנס ולא יוצא זורם) כך שנוכל לפשט את האינטגרל על הספיקה:

נניח פרופיל מהירות אחיד , ונשים לב ש- . נקבל:

גם שטח המיכל הוא מעגלי, כך ש- . נציב ונקבל כי:

סעיף ב’

מאחר ואנו מזניחים צמיגות ובמיכל מניחים שהזרימה חד-ממדית בכיוון , משוואות נאוויה-סטוקס בכיוון יהיו:

נניח שהזרימה מפותחת (לא יודע איך אחרת לפתור את זה, אבל זה גם נשמע הגיוני) - . נישאר עם:

צד ימין תלוי רק ב-, ולכן כאשר נבצע אינטגרציה לפי , נוכל להתייחס לביטוי בצד ימין כקבוע.

נציב תנאי שפה:

ולכן:

כאשר נשים לב ש:

סעיף ג’

באותו אופן כמו סעיף קודם, נקבל כי:

מאחר ולמיכלים גאומטריות זהות, נסיק שקצב שינוי הגובה במיכל אחד הוא מינוס קצב שינוי הגובה במיכל השני:

ולכן פילוג הלחצים הוא:

נציב תנאי שפה ונקבל ש:

כאשר נשים לב ש:

סעיף ד’

בצינור, נניח:

1. זרימה חד-ממדית - .
2. הזרימה מפותחת, כך ש- .
3. כבידה זניחה.
4. צמיגות זניחה.

לכן, משוואות נאוויה-סטוקס בכיוון יהיו:

צד שמאל של המשוואה תלוי רק ב-, כך שנוכל להתייחס אליו כקבוע כאשר נבצע אינטגרציה לפי :

מסעיפים קודמים, נסיק שתנאי השפה הם:

נשווה בין ה- שקיבלנו:

מסעיף א’ אנו יודעים ש- . ולכן:

בנוסף, מהנתונים נסיק כי . נציב:

או, כמו שכתוב בפתרון הרשמי:

הערה:

מאמין שיש טעות בפתרון הרשמי - החישוב של צריך להיות בסימן הפוך.

סעיף ה’

ברוכים הבאים לקורס מד”ר. נוכל להגדיר משתנה שיהפוך את המד”ר להומוגנית - :

אם נסמן:

אז נוכל לרשום את המד”ר בצורה הבאה:

רק בזכות יזהר אני זוכר שהפתרון למד”ר הזה הוא:

נחזור בחזרה לביטוי עבור :

לפי הנתונים, תנאי ההתחלה הם ו- . לכן:

נציב בחזרה:

אין לי שמץ של מושג למה שגובה המים ישתנה באופן הרמוני עם הזמן.