FLD1_006 צמיגות

→ קודם: FLD1_005הבא: FLD1_007 ←

גבול הצמיגות ומשוואות סטוקס

גבול הצמיגות

נביט במשוואות נאוויה-סטוקס המנורמלות:

נאמר שאנחנו תחת גבול הצמיגות כאשר הצמיגות של הנוזל יותר דומיננטית מהאינרציה:

ואז נוכל להזניח את ביטוי האינרציה .

אם מתקיים גם שהצמיגות יותר דומיננטית מהכוחות גוף:

אז נוכל אפילו להזניח גם את ביטוי הכוחות גוף .

נסיק שכדי לקיים את שני התנאים, צריך לקיים:

כאשר אנו תחת הגבול הצמיגי והכבידה זניחה, משוואות נאוויה-סטוקס הופכות להיות מהצורה:

נשווה את המקדמים:

נקבל ביטוי עבור הגודל האופייני של הלחץ:

לגודל זה אנו קוראים הלחץ האופייני של הגבול הצמיגי.

דוגמה:

חרק בתוך דבש באורך זז במהירות כאשר:

תחת איזה גבול נוכל לתאר את הבעיה, ומהו הלחץ האופייני?
פתרון:
כדי לקיים את גבול הצמיגות, וכבידה זניחה.

נציב נתונים:

ואכן מקיים את תנאים אלו.
נמצא את הלחץ האופייני:

משוואות סטוקס

תחת הגבול הצמיגי, אנו יכולים להניח שצמיגות הנוזל היא הדומיננטית בתיאור התנועה שלו.

משפט:

משוואות סטוקס קובעות כי עבור נוזל תחת הגבול הצמיגי מתקיים:

כאשר הוא גרדיאנט הלחץ; הוא צמיגות הנוזל; הוא שדה המהירות.

פיתוח:
כאשר אנו תחת הגבול הצמיגי, והכבידה זניחה, משוואות נאוויה-סטוקס הופכות להיות מהצורה:

מהשוואת הוקטורים המנורמלים:

והמשוואה הממדית היא:

למה ה- חזר?

התהליך של נרמול “מוציא” את הממדים הפיזיקליים (מטרים, שניות, ניוטון…) מהמשוואה, כך שאנו נשארים עם משוואות חסרות ממד. נשים לב שאת אנחנו לא מנרמלים (וגם את למשל). כאשר אנו רוצים להחזיר בחזרה את הממדים, הצמיגות חייבת לחזור כדי להציג בצורה נכונה את הממדים הפיזיקליים של הנוזל.

הנחת גופים דקים

כל הפיתוחים עד כה בעזרת נרמולי משוואות נאוויה-סטוקס נעשו בהנחה שנרמלנו את גדלי המרחב כולם באותו אורך . אבל, אם היינו מנרמלים את הגדלים באופן שונה בכל כיוון, יכל להיות שנקבל עוד מידע על הבעיה שלנו.
שיטה זו מאוד שימושית עבור אנליזת גופים דקים:

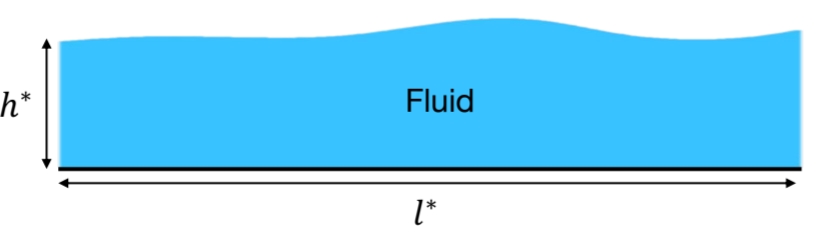
גוף דק באורכים אופייניים ו-.

בגוף דק, כאשר חלקו הארוך בכיוון ואורך אופייני , וחלקו הצר בכיוון ואורך אופייני , נוכל להגדיר את היחס בינהם:

עבור גוף דק, אנו מניחים ש- .
במקרה הדו-ממדי הנתון, אנו מבצעים את הנרמולים הבאים:

נבצע כעת נרמול של חוק שימור המסה הדיפרנציאלי:

מאחר והגדלים הם מנורמלים (בסדר גודל ), נוכל להניח ש:

נציב את ביטוי זה ואת כל הנרמולים למשוואות נאוויה-סטוקס. לאחר מספר פיתוחים נקבל משוואות מאוד דומות למשוואות נאוויה-סטוקס המנורמלות:

כאשר הפעם, מופיע מספר ריינולדס המוקטן:

הערה:

יש כמה דרכים שונות לרשום את ריינולדס המוקטן ביחס לריינולדס הרגיל:

כאשר ו- . אמיר אוהב לרשום עם , וישראל מעדיף לרשום עם , שזה למעשה אותו הדבר.

נשים לב שכל הביטויים שמופיעים עם ניתנים להזנחה - הרי אנו מניחים ש-. נישאר עם:

קירוב הלובריקציה

כאשר נדרוש גם את הנחת גופים דקים, וגם את גבול הצמיגות, נאמר שאנו בגבול הלובריקציה.

משפט:

תחת גבול הלובריקציה, משוואות סטוקס הופכות להיות:

כאשר הוא הכיוון הארוך, ו- הוא הכיוון הקצר.
במקרה של שני ממדים ארוכים וממד אחד קצר , נקבל:

במקרה של גאומטרייה גלילית ארוכה, כך ששני הממדים הקצרים הם , והממד הארוך הוא , נקבל:

או, בקואורדינטות פולאריות (כאשר הוא הממד הארוך):

פיתוח:
נפתח רק עבור המקרה הדו-ממדי.
בכיוון , משוואות גופים דקים הופכות להיות:

מהשוואות סדרי גודל ומקדמים, נסיק כי במקרה הלא מנורמל:

בכיוון , משוואות גופים דקים הופכות להיות:

זרימות נפוצות

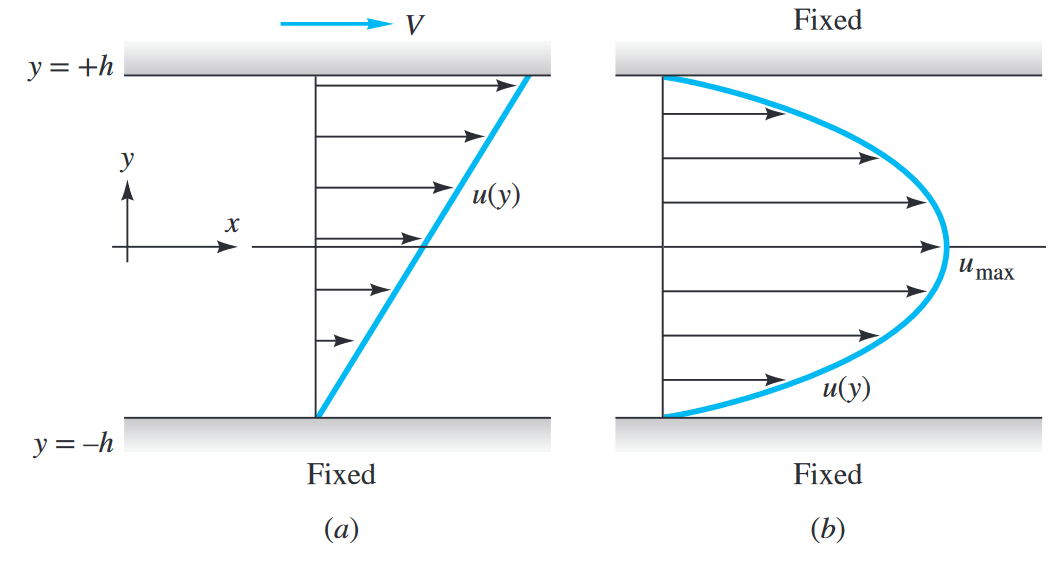
זרימה בין שתי פלטות

נביט בזרימה הבאה:

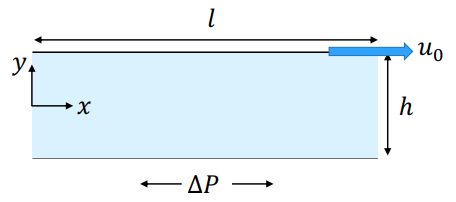
זרימה דו ממדית של נוזל בלתי דחיס, ניוטוני, בגוף דק המקיים את הנחות הלובריקציה.

לפי קירוב הלובריקציה ומשוואת הרצף:

כדי לפתור בעיה כזאת, נצטרך גם להגדיר תנאי שפה.
בהתחלה ובסוף המסלול, נגדיר את הלחצים:

הנוזל לא חודר את הפלטות, ולכן:

נניח את תנאי אי-ההחלקה:

מאחר ו- , נוכל לומר ש- לא תלוי ב-. כלומר, . לכן לא נסתבך כאשר נבצע אינטגרציה ל- פעמיים:

ולכן:

נציב תנאי התחלה ו- :

נציב בחזרה:

ניתן להראות מחוק שימור המסה האינטגרלי שאם קבוע, אז גם קבוע, ולכן:

נציב תנאי התחלה ונקבל:

לכן . נציב ב- ונקבל:

הספיקה הנפחית, שהיא פשוט אינטגרציה על המהירות , תהיה נתונה ע”י:

תוצאה זו היא למעשה סופרפוזיציה של שני סוגי זרימה בסיסיים:

1. זרימת קואט .
2. זרימת פואזיי .

נבחן כל אחת מהזרימות בנפרד.

זרימת קואט (Couette)

כאשר אין שינוי בלחץ לאורך (), נקבל שפרופיל המהירות הוא:

פרופיל המהירות לינארי

זרימת פואזיי (Poiseuille)

כאשר הפלטות לא זזות אחת ביחס לשנייה (), נקבל שפרופיל המהירות הוא:

פרופיל המהירות פרבולי

זרימה בין שתי פלטות; (a) זרימת קואט; (b) זרימת פואזיי. (Fox & Mitchell, 2019).

זרימת האגן-פואזיי

סימולציה של זרימת האגן-פואזיי (Laminar Pipe Flow (Hagen Poiseuille) | Validation Case, n.d.)

נביט בזרימה של נוזל ניוטוני, אקסיסימטרי, בצינור דק, כך שנוכל להשתמש בקירוב הלובריקציה. לפי קירוב הלובריקציה ומשוואת הרצף בקואורדינטות פולאריות:

מהצבת תנאי שפה (אי חדירה ואי החלקה) נקבל:

זרימת טיילור-קואט

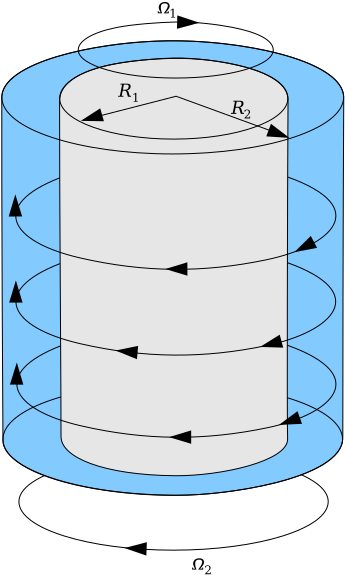
מערכת זרימת טיילור-קואט

פיתוח של פרופיל המהירות נמצא בשאלה 2.

לינאריות משוואות סטוקס

ניזכר במשוואות סטוקס:

נשים לב שזוהי מערכת מד”ח לינארית, גם כאשר נתחשב במשוואת הרצף. לתכונה זו של משוואות סטוקס משמעות עצומה להתנהגות בעיות תחת הגבול הצמיגות.

נביט למשל בבעיה הבאה (תחת הגבול הצמיגי):

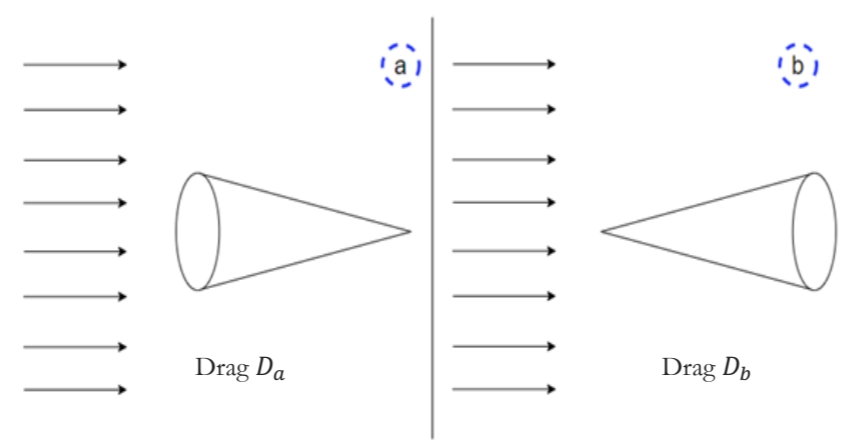
שתי זרימות הפוכות עבור אותה הגאומטרייה.

מה נוכל להסיק מלינאריות משוואות סטוקס על הפרש כוח הגרר (הכוח שהנוזל מפעיל על המוצק) ?

מאינטואיציה, נוכל לנחש שעל גוף יפעל יותר כוח גרר כי הוא פחות “אווירודינמי”. אבל, בגבול הצמיגי אנחנו בעולם אחר - עולם שבו האינטואיציה שלנו נשברת כי אנחנו לא רואים הרבה תנועות צמיגיות ביום-יום.

למעשה, מה שיקרה הוא שכוח הגרר זהה - , ומסקנה זו נובעת מהלינאריות של משוואות סטוקס. הרי ממשוואות סטוקס יש קשר לינארי בין כוח הגרר למהירות הזורם:

לפיכך, אם פשוט נחליף את סימן המהירות ל- , נקבל כוח גרר הפוך - . במקרה שלנו גם הפכנו את כיוון הבעיה, שלילי על שלילי הוא חיובי, ונקבל .

משוואות ריינולדס

משפט:

משוואת ריינולדס הכללית לנוזל ניוטוני בלתי דחיס, תחת גבול הצמיגות, ובגוף דק כך ש- הוא הממד הקצר שלו ו- הוא גובה ממד זה:

במקרה הדו-ממדי:

פיתוח:
נתחיל ממשוואות הלובריקציה, כאשר המידה הקצרה היא בכיוון , והמידות הארוכות הן :

לאחר אינטגרציה פעמיים לפי של שתי המשוואות הראשונות, שימוש במשפט היסודי של החדוא, הצבת תנאי שפה והצבה במשוואת הרצף:

ריינולדס לבעיות אקסיסימטריות

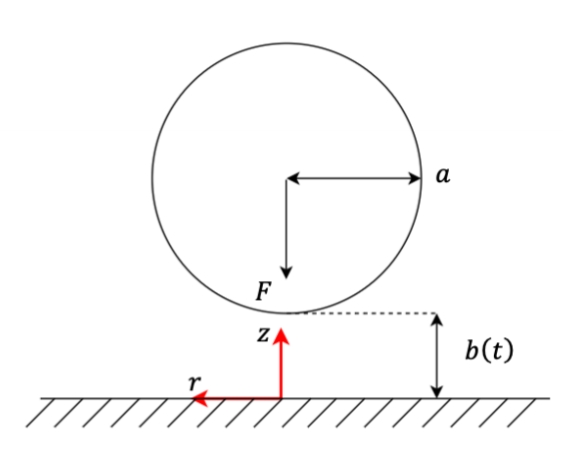
במקרה אקסיסימטרי אין הבדל בכיוון , ולכן . נקבל שמשוואת ריינולדס הופכת להיות מהצורה:

ריינולדס לבעיות מסתובבות

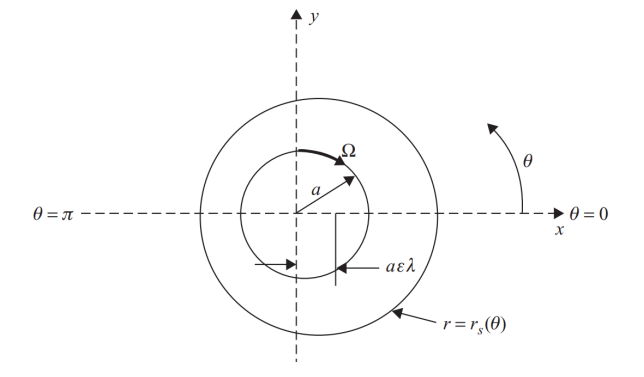
במקרה פולארי, אבל לא אקסיסימטרי (גופים מסתובבים -מיסב), כאשר הגוף הפנימי מסתובב במהירות זוויתית , והגוף החיצוני נמצא בהטיה שגודלה ממרכז הגוף הפנימי, משוואת ריינולדס הופכת להיות מהצורה:

תרגילים

שאלה 1

זורם בעל צפיפות ועובי נע במורד מישור ארוך, הנטוי בזווית בהשפעת הכבידה כפי שמתואר באיור. ידוע כי , כאשר הוא אורך האופייני של המישור.

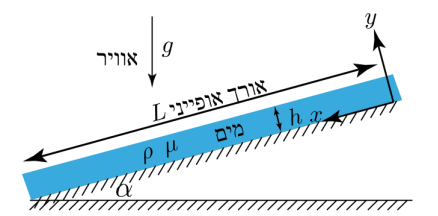
סכימת המישור

סעיף א’

מצאו את פילוג המהירות בשכבת הזורם.

פתרון:
נניח את ההנחות הבאות:

1. הצפיפות קבועה -
2. הבעיה בדו-ממד.
3. מצב מתמיד - .
4. הזרימה מפותחת - . במקרה הדו-ממדי:

נתחיל מחוק שימור המסה הדיפרנציאלי (לדו-ממד):

אנו הנחנו שהזרימה מפותחת, כך שהאיבר הראשון מתאפס. נשארנו עם:

במערכת צירים הצמודה למשטח, הנוזל לא יכל לחדור את המישור המוצק - כלומר, מתקיים . נסיק ש- .

נוכל כעת לחשב את משוואות נאוויה-סטוקס בכיוון :

כאשר איפסנו את כל האיברים הנ”ל על בסיס ההנחות והמסקנות שהגענו אליהן. למשל, כי אנו במצב מתמיד.
נישאר עם:

במקרה שלנו, מדג”ח זריז, מתקיים . לכן:

אינטגרציה לפי :

כל החלק העליון של הנוזל נמצא בלחץ אטמוספרי. לפיכך, נוכל להציב את התנאי שפה , ונסיק גם ש- בכלל לא תלוי ב-, הוא פשוט קבוע:

נציב בחזרה בביטוי עבור :

נעבור למשוואות נאוויה-סטוקס בכיוון :

כאשר איפסנו את כל האיברים הנ”ל על בסיס ההנחות והמסקנות שהגענו אליהן. ביטלנו גם את כי מצאנו ש- לא תלוי ב-.
נשארנו עם:

מדג”ח זריז, אנו יודעים ש- . נציב, ונקבל מד”ר:

לאחר פתירת המד”ר נקבל:

נותר למצוא תנאי שפה.

1. מתנאי אי-החלקה, אנו יודעים ש- .
2. על שפת הנוזל קיימת שפה חופשית - לא פועלים עליה כוחות. בנוזל ניוטוני בדו-ממד, ראינו כי המאמץ שפה על נוזל מוגדר ע”י: במקרה שלנו, אנו יודעים ש-, וגם ש- . נסיק ש:

עם שני תנאי שפה אלו, נוכל למצוא את הקבועים , ונקבל:

סעיף ב’

מצאו את הספיקה הנפחית (ליחידת עומק) במקרה זה.

פתרון:
ספיקה נפחית ניתן למצוא מאינטגרציה על המהירות:

שאלה 2

שני גלילים קונצנטריים מכילים במרווח ביניהם זורם בעל צפיפות . הגליל הפנימי בעל רדיוס מסתובב במהירות זוויתית קבועה , והגליל החיצוני בעל רדיוס מסתובב במהירות זוויתית קבועה .

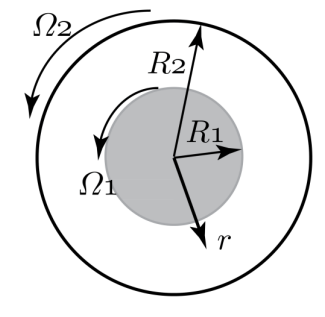
סכימת הגלילים

סעיף א’

מצאו את פילוג המהירות של הזורם.

פתרון:
נניח את ההנחות הבאות:

1. הצפיפות קבועה -
2. הזרימה דו-ממדית
3. אקסיסימטריה -
4. כבידה זניחה
5. מצב מתמיד -

לפי חוק שימור המסה הדיפרנציאלי (בקואורדינטות פולאריות):

כאשר איפסנו את הביטויים לפי ההנחות (שמספרם תואם לביטול). נשארנו עם:

כדי למצוא את הקבוע, נוכל מתנאי השפה של אי-חדירה למצוא כי:

ולכן . נסיק כי:

לפי משוואות נאוויה-סטוקס בכיוון (במקרה הדו-ממדי):

נשארנו עם מד”ר:

נפתור ונקבל:

את תנאי השפה נוכל למצוא מהנתונים על מהירויות השפות:

נקבל כי:

סעיף ב’

עבור ו-, מצאו את הביטוי לגרדיאנט הלחץ במערכת.

פתרון:
נרשום את משוואות נאוויה-סטוקס בכיוון :

כאשר איפסנו את הביטויים לפי ההנחות (שמספרם תואם לביטול). נשארנו עם:

שאלה 3

נתונה תעלה דו ממדית בעלת אורך וגובה הנמצאת בסביבה אטמוספרית ומכילה נוזל פרו-מגנטי בעל צמיגות וצפיפות .
נתמקד במקרה בו השדה המגנטי יוצר כוח גוף לינארי מהצורה בכיוון ציר כאשר הינו עוצמת השדה המגנטי ו- קבוע יחידות תואמות.

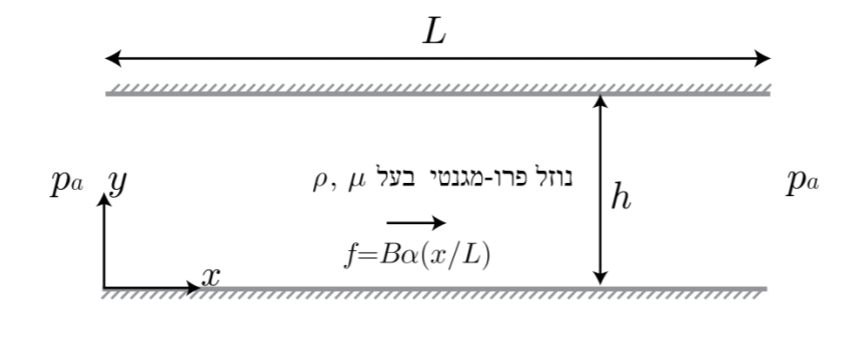
סכימת התעלה

סעיף א’

בהנחה כי אינרציית הזורם זניחה:

1. מצאו את המשוואה המנורמלת השולטת במהירות בין הפלטות.
2. מצאו ביטויים למהירות וללחץ האופייניים במערכת.

פתרון:
נתחיל ממשוואת הרצף:

ננרמל ע”י הגדלים האופייניים הנתונים:

נציב במשוואת הרצף:

שני האיברים המנורמלים (חסרי ממד) הם בסדר גודל , כך שנוכל לבצע “השוואת מקדמים”:

ולכן:

נשים לב שמהנתונים מתקיים , כך שבעצם מתקיים:

מבחינת האיברים החסרי ממד:

נעבור למשוואות נאוויה-סטוקס למקרה הדו-ממדי, בכיוון :

מאחר והאינרציה זניחה, כל אגף שמאל מתבטל. בנוסף, נשים לב ש- :

ננרמל באותו אופן:

אנו כבר יודעים ש-, ומאחר ו- , נוכל לבטל את הביטוי של :

כיוון שאנו מנורמלים, לכל איברי המשוואה סדר גודל , כך שלמעשה מתקיים שכל המקדמים שווים (בערך):

לא כל כך הבנתי? איך אפשר לומר שהם כולם בערך שווים?

תאכלס, מבחינה מתמטית, אי אפשר באמת לומר את זה. אבל, בכל זאת, נוכל להסיק זאת מפיזיקליות הבעיה.
אם המשוואה הייתה יותר פשוטה, למשל מהצורה:

אז היינו יכולים לומר שהמקדמים בערך מאותו סדר גודל, אחרת המשוואה לא הייתה מתקיימת:

הבעיה היא שבמקרה שלנו ישנם שלושה ביטויים, ואז המשוואה יכולה להתקיים גם אם כל המקדמים בערך באותו הסדר גודל, אבל גם אם אחד מהמקדמים זניח ביחס לאחרים. למשל, אם . אז שוב, איך אנחנו יכולים לומר שכל המקדמים למעשה בערך באותו הסדר גודל?
הסיבה היא פיזיקלית. אנו יודעים שאם זניח, אז המהירות של הזורם גם כן אפסית. אנו גם יודעים שאם יש הפרש לחצים, אז יש מהירות. כלומר, כל שלושת האיברים בוודאות משחקים כאן תפקיד במשוואה, ואי אפשר להזניח את אחד מהם, כי אז הבעיה פשוט לא תהיה פיזיקלית.

ולכן:

בנוסף, מבחינת הערכים המנורמלים:

סעיף ב’

רשמו את התנאי על עוצמת השדה המגנטי על מנת שההנחה מסעיף א’ (אינרציה זניחה) תהיה נכונה.

פתרון:
כדי שהאינרציה תהיה זניחה, נדרוש שמספר ריינולדס המוקטן יקיים :

נציב את המהירות האופיינית כדי לקבל:

סעיף ג’

בהנחה כי , הראו כי .

פתרון:
מפתרון סעיף א’, מבחינת הערכים המנורמלים (לצורך פשטות, נעבור לסימון של , למרות שהכוונה היא עדיין לערכים מנורמלים).

אם אנו מניחים ש- , אז כל אגף שמאל תלוי רק ב- ונוכל לסמן . כלומר:

לאחר אינטגרציה פעמיים:

מתנאי אי החלקה:

נציב את התנאים:

נציב בחזרה ונקבל:

עדיין לא נפטרנו מה-. נבחר נפח בקרה כללי בתוך הצינור.

בחירת נפח בקרה קבוע.

לפי חוק שימור המסה האינטגרלי (כאשר נשים לב שנפח הבקרה קבוע):

מאחר ובחרנו כלליים, נוכל להסיק ש:

נציב את הביטוי שמצאנו ל-:

נסמן , ונקבל כי:

שאלה 4

נתונה תעלה צרה וארוכה שמורכבת משני מסועים בעלי 4 גלגלים ברדיוס המסתובבים במהירות זוויתית כמתואר בציור. הודות לסיבוב, האוויר מהסביבה (שנמצאת בלחץ אטמוספרי) נשאב אל תוך התעלה. ניתן להניח כי גובה התעלה, , קטן משמעותית מאורך התעלה . האוויר בעל צמיגות וצפיפות . ניתן להזניח אפקטי קצוות וכבידה.
ניתן גם להניח שהאינרציה זניחה.

סכימת המסועים

סעיף א’

מצאו את פילוג המהירות בתעלה.

פתרון:
ממשוואת הרצף:

נבצע את הנרמולים הבאים:

נשים לב ש , ונציב:

מסדרי גודל, נוכל לומר ש:

נעבור למשוואות נאוויה-סטוקס למקרה הדו-ממדי, בכיוון :

האינרציה זניחה, כך שאגף שמאל מתבטל. בנוסף, נתון כי אין כוחות גוף:

נציב נרמולים ונקבל:

כיוון ש- , נוכל להזניח את :

נשווה מקדמים ונקבל כי הלחץ האופייני:

מבחינת הגדלים המנורמלים:

לכן והמשוואה הלא מנורמלת היא:

כאשר נבצע נרמול גם עבור משוואות נאוויה-סטוקס בכיוון , נקבל:

כלומר, אנחנו מבצעים כאן את קירוב הלובריקציה.

הערה:

זהו בדיוק אותו התהליך שעשינו בקירוב הלובריקציה. הוא מופיע כאן שוב כי חשוב לתרגל את זה… אולי? לא מרגיש שיש תיאום בין המרצה למתרגלים.

כעת נעבוד כמו בזרימה בין שתי פלטות, כאשר הפעם התנאי שפה שלנו הם:

• תנאי שפה של לחצים זהים:
• תנאי שפה של אי החלקה:

כמו בפיתוח בזרימה בין שתי פלטות, פרופיל הלחצים נתון ע”י:

ובמקרה שלנו:

כך שבעצם מתקיים . לכן המהירות (שוב, מביטוי שפיתחנו לאחר אינטגרציה פעמיים בזרימה בין שתי פלטות):

נציב תנאי שפה:

כלומר, המהירות קבועה:

סעיף ב’

מוסיפים שני קירות נייחים בעלי אורך בקצה של התעלת מסועים. מצאו את פילוג המהירות בכל אחד מחלקי התעלה.

סכימת המסועים ושני הקירות

פתרון:
בשני האזורים, עדיין מתקיים:

ולכן המד”רים מסעיף קודם עדיין מתקיימים:

נסמן את הלחץ בין שני האזורים ב-.

• עבור אזור שני הקירות הנייחים:
  תנאי ההתחלה:

  נציב ונקבל כי (לפי זרימת פואזיי):

• באזור של המסועה:
  תנאי ההתחלה:

  נקבל שהפתרון הוא:

הערה:

העובדה שקיבלנו ו- מאוד דומים לא מפתיעה. ה- שקיבלנו סעיף קודם () הוא כאשר רק התנאי שפה על הומוגניים. הוא כאשר רק התנאי שפה על הומוגניים. אז , שהוא מגיע מסכום של שני תנאי השפה של ו-, יהיה פשוט הסכום של ו-.

נותר למצוא מהו . מחוק שימור המסה האינטגרלי (נפח בקרה קבוע על היציאה והכניסה):

נקבל שהלחץ :

סעיף ג’

עתה, מכניסים “פקק” ביציאה הימנית של שני קירות (נייחים). מצאו את פילוג המהירות החדש במצב מתמיד בכל אחד מחלקי התעלה.

פתרון:
משימור מסה (אינטגרלי) על האזור של הקירות, קל לראות כי:

נבין שכעת באזור של הקירות אין מהירות. אבל הפתרון שלנו עבור האזור של התעלת מסועים, , עדיין תקף:

רק הפעם שונה.
משימור מסה על אזור של התעלת מסועים:

נציב את ונקבל:

→ קודם: FLD1_005הבא: FLD1_007 ←