FLD1_HW002 תרגיל בית 2

	סטודנט א’
שם	עידו פנג בנטוב
ת”ז	CLASSIFIED
דואר אלקטרוני	CLASSIFIED

שאלה 1

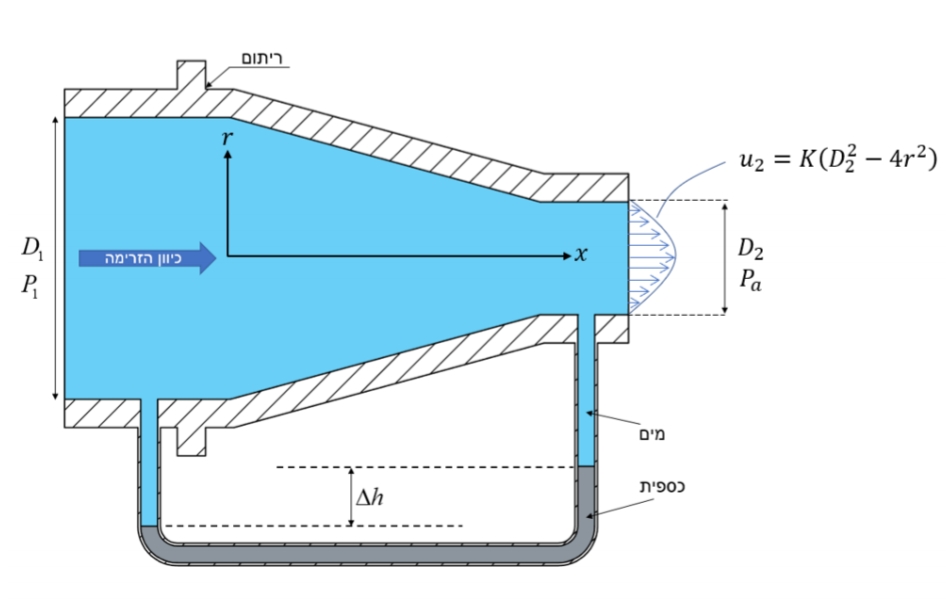
סכימת הצינור

סעיף א’

נבחר כנפח בקרה את נפח הצינור. לפי חוק שימור המסה האינטגרלי:

נבחין כי הנפח בקרה לא משתנה עם הזמן, וצפיפות המים אחידה לאורך הנפח, כך שהאינטגרל הראשון מתאפס. בנוסף, ישנה כניסה ויציאה אחת עם מהירויות ונורמלים ידועים:

נחלק ב-, ונציב את המהירויות הנתונות:

מגאומטריית הכניסות:

סעיף ב’

לפי חוק שימור התנע האינטגרלי:

נפח הבקרה קבוע עם הזמן, וצפיפותו אחידה, כך שהאינטגרל בצד שמאל מתאפס:

נפרק את לכוחות שפה וכוחות גוף. נשים לב שלא קיימים כוחות גוף בכיוון , ולכן נוכל להישאר רק עם כוחות שפה:

מבחינת המהירויות בכניסה וביציאה, הם נתונות, ושתיהן בכיוון :

נציב את הפתרון מסעיף קודם:

נציב בשימור התנע האינטגרלי ונקבל:

מבחינת כוחות על השפה, אנו יכולים לפרק ללחצים בכניסה וביציאה, ולכוח שהמוצק מפעיל על הנוזל, שנסמן :

נרצה כעת למצוא את .

דג”ח אופקי על הנפח בקרה

למה שרטט את הכוחות ככה?

את הדג”ח אנחנו עושים על מוצק - אף פעם לא על הנוזל, כי זה די מסובך להגדיר דג”ח על נוזל. לפיכך, הלחץ בכניסה, , לא מופיע בדג”ח, וגם הלחץ ביציאה, פועל רק איפה שיש מוצק.
כדי להבין למה אני לא משרטט את הלחץ האטמוספרי כנורמלי למשטח, ולמה בכלל אני מכפיל אותו בשטח של טבעת בהמשך, קראו את משטחים טבולים.

משקול כוחות (הצינור לא זז בגלל הריתום):

כאשר הוא הכוח שהנוזל מפעיל על המוצק. נשים לב שהוא נגדי לסך הכוח שהמוצק מפעיל על הנוזל:

הסבר יותר מפורט על סכימת הלחץ לאורך הצינור נמצא במשטחים טבולים.
נציב בשימור תנע:

נרצה לחשב את . נמצא את הלחצים לאורך תחתית המיכל בעזרת משוואות ההידרוסטטיקה (נוכל לעשות זאת כי נתון שבתחתית המיכל המהירות אפסית).

למה לא לבחור פשוט קו זרם בחלק העליון של הנפח בקרה?

בעייתי. לא נתון לנו שום דבר על שדה הזרימה בתוך הצינור - מבחינתנו הוא חור שחור. אבל, בתחתית הצינור נתון לנו שאין זרימה כמעט (במנומנטר). הכניסה והיציאה של המנומטר מספיק קרובים ליציאה ולכניסה כך שנוכל לשרטט שם קווי זרימה.
עוד סיבה היא שלא נתון שצמיגות הזורם זניחה, ולכן לא נוכל להשתמש בכלל במשוואת ברנולי.

עבור הפרשי הגבהים במים נבנה את פילוג הלחץ הנ”ל (לפי הידרוסטטיקה):

כלומר, בכל נקודה במים, הסכום הוא קבוע, כך שנוכל להשוות בין כל שתי נקודות במים.
עבור גבהים :

עבור גבהים :

באותו אופן עבור , רק שהפעם מדובר בצפיפות :

נסכום את כל שלושת המשוואות:

נשים לב ש- . מבחינת המידות הנתונות, יוצא ש- קטן משמעותית מהגודל . לכן, נוכל להזניח אותו בחישוב שלנו.

נישאר עם:

נציב בביטוי שקיבלנו עבור , כאשר נשים לב שבביטוי זה ה- שרשמנו מתייחס ל-:

בשאלה שואלים לא על הריאקציה שפועלת על הצינור, אלא על הריאקציה שפועלת על הריתום, שזה הפוך מה- שקיבלנו:

אם נציב נתונים, נקבל:

שאלה 2

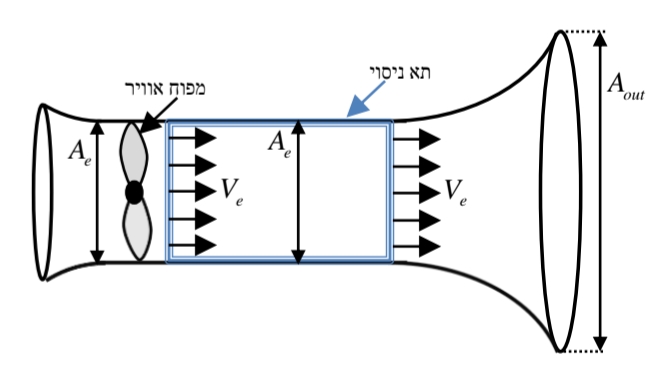
סכימת המנהרת רוח

נבחר את האזור סביב המפוח כנפח בקרה.

בחירת נפח הבקרה. ו- הם הלחצים בכניסה והיציאה, ו- הוא הכוח שמפעיל המפוח.

לפי חוק שימור התנע האינטגרלי:

נפח הבקרה קבוע עם הזמן, וצפיפותו אחידה (הזרימה בלתי דחיסה), כך שהאינטגרל בצד שמאל מתאפס. בנוסף, נשים לב שלפי שימור מסה זריז, קל לראות שאם הנוזל ביציאה במהירות , אז גם המהירות בכניסה הוא . לפיכך, האינטגרל הימני בצד ימין גם כן מתאפס. בכיוון , נשארנו עם:

את בכיוון נוכל לפרק לכוח שמפעילים הלחצים בכניסה וביציאה, וגם לכוח שמפעיל המפוח על הנוזל:

את הפרש לחצים זה נוכל למצוא ממשוואת ברנולי על כל חלק נפרד של המנהרה. עבור הכניסה למנהרה והכניסה למפוח:

נניח גם שמהירות האוויר בכניסה למנהרה “עומדת”, כלומר, זניחה, כך ש- :

ברנולי עבור היציאה מהמפוח עד ליציאה מהמנהרה:

משימור מסה זריז מהיציאה מהמפוח עד ליציאה מהמנהרה ניתן למצוא ש:

נציב בחזרה בברנולי ונקבל:

נהפוך את הצדדים של המשוואה:

כעת נוכל לחסר בין (3) ל-(2):

נציב ב-(1):

שאלה 3

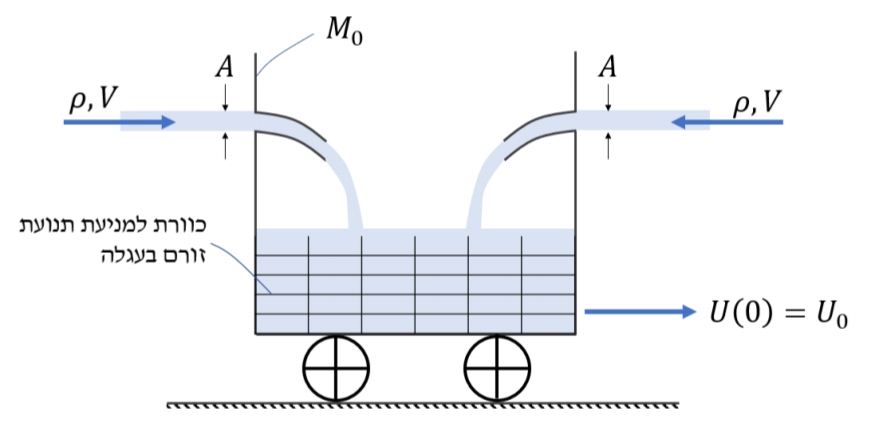
סכימת העגלה

נבחר בעגלה כנפח הבקרה, ואת מערכת הצירים צמודה לעגלה. לפי חוק שימור התנע האינטגרלי:

המהירות של הנוזל בנפח הבקרה, ביחס למערכת הצירים, היא זניחה (נתון מקיום הכוורת בעגלה). לכן, האינטגרל בצד שמאל מתאפס:

ישנן שתי כניסות לנפח הבקרה, עם מהירויות נתונות. נשים לב שהן נתונות במהירותן ביחס למערכת צירים קבועה, אז נצטרך לתקן אותם למערכת צירים הנעה. בנוסף, נשים לב שהתנועה של הנפח בקרה הוא רק בכיוון , כך ש-.

לפי חוק שני של ניוטון (במערכת צירים לא אינרציאלית):

המערכת צירים שלנו צמודה לנפח בקרה, ולכן מבחינתה, . לכן:

נשים לב שהמסה כעת משתנה עם הזמן. לפי חוק שימור המסה האינטגרלי:

הביטוי בצד שמאל הוא למעשה ספיקת המסה - . בנוסף, ישנן שתי כניסות לנפח בקרה עם מהירויות נתונות (ביחס לנפח בקרה):

נבצע אינטגרציה, כאשר נשים לב ש- :

נציב בחוק שני:

נציב בשימור תנע:

סעיף ב’

נסדר את הפתרון הקודם:

זוהי משוואה פרידה:

נציב תנאי התחלה :

נציב ונקבל:

סעיף ג’

נחזור על אותם השלבים מסעיפים קודמים. עבור שימור תנע:

נתון שהספיקה היוצאת מהעגלת ע”י המשאבה זניחה יחסית לספיקה הנכנסת דרך הזרנוקים, כך שמסת העגלה כתלות בזמן היא עדיין:

ולכן חוק שני עדיין:

נציב בשימור תנע:

זוהי כבר לא משוואה פרידה. נעבור לשיטת גורם אינטגרציה. הג”א:

נכפיל במד”ר:

נציב את התנאי התחלה :

ולכן:

שאלה 4

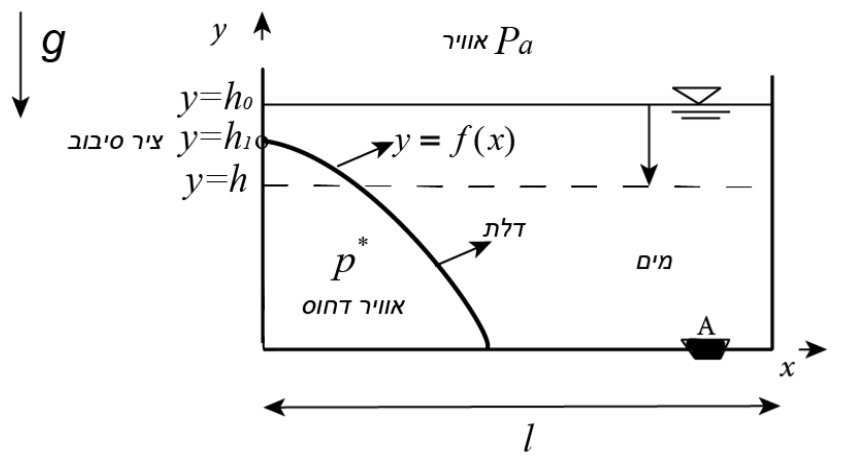
סכימת המיכל

סעיף א’

מצב הנוזל במיכל הוא הידרוסטטי, ולכן לפי מערכת הצירים שנבחרה, עבור גובה כללי בנוזל מתקיים:

כאשר את נוכל למצוא מהתנאי שפה על גובה מפלס המים - :

לכן, בנוזל:

סעיף ב’

נשים לב שעל הדלת פועלים לחצים משני הכיוונים - לכיוון החיובי, ו- לכיוון השלילי. לפי משטחים טבולים:

נציב את שמצאנו בסעיף קודם, כאשר אנו מניחים ש- :

נתון כי הדלת בעלת צורה פרבולית . נסיק מכך ומגאומטריית שגבולות האינטגרציה שלנו צריכים להיות ו- :

לכן, ליחידת עומק :

סעיף ג’

באותו אופן כמו סעיף קודם:

נרצה למצוא את גבולות האינטגרציה. כלומר, נרצה למצוא את החיתוך עם ציר ה- של :

מגאומטריית הדלת, אכפת לנו מ- . נסיק כי:

ממשוואת הדלת אנו יודעים שלאורך הדלת . נציב:

לכן ליחידת עומק :

סעיף ד’

סכימת הדלת

כדי שהדלת תפתח, שקול המומנטים סביב הציר צריך להיות גדול מאפס (עבור מומנט שלילי הדלת גם לא תפתח - הרצפה מונעת ממנו). נמצא מתי מומנט זה שווה לאפס:

כאשר הוא הכוח המפורס הפועל במרחק מהציר.

תיאור הכוח המפורס כסכום הלחצים בכיוון הנורמל למשטח.

במקרה שלנו, הכוח המפורס הוא:

כאשר הוא הכיוון הניצב ל-.

נציב ונקבל:

נוכל כעת להתעלם מהכיוון ולהסיק ש:

נשים לב שהאינטגרציה מתבצעת מ- ל-, ולכן:

הגודל הוא קבוע ולכן נוכל לפתור אותו קודם:

נציב את הביטוי עבור מסעיף א’, כאשר נניח שגובה מפלס המים שווה ל- :

נשים לב ש- לאורך גאומטריית הדלת. נציב:

סעיף ה’

נפתור בצורה דומה לשאלה 3 בחוקי שימור אינטגרליים.
נבחר נפח בקרה צמוד לגובה מפלס המים, אבל חסום ע”י פתח הפקק:

בחירת נפח הבקרה

לפי חוק שימור המסה האינטגרלי:

נפח הבקרה משתנה עם הזמן, כך שבין ל-:

כיוון שבחרנו בנפח בקרה צמוד לגובה מפלס המים, אין כניסה מלמעלה. כלומר, ישנה רק יציאה אחת - מהפתח:

נציב בחזרה בשימור מסה:

נוכל למצוא את ממשוואת ברנולי. נבחר שתי נקודות באותו קו זרם, אחת על מפלס המים והשנייה ביציאה. נקבל:

בפתח אנו יודעים ש- . בנוסף, מהירות מפלס המים זניחה. לכן:

נציב בחזרה בשימור מסה:

זוהי משוואה פרידה:

נציב תנאי התחלה :

נסיק כי:

סעיף ו

נחזור על אותם השלבים, רק הפעם נשים לב שפרופיל נפח הבקרה שלנו שונה.
לפי חוק שימור המסה האינטגרלי:

קצב שינוי נפח הבקרה:

מגאומטריית נפח הבקרה ניתן לראות ש:

נציב ונקבל:

כמו בסעיף קודם, ישנה רק יציאה אחת - מהפתח:

מהירות היציאה לא השתנתה:

נציב בחזרה בשימור מסה:

שוב קיבלנו משוואה פרידה:

נציב תנאי התחלה :

נציב בחזרה:

נרצה לדעת מתי :