| קורס | מכניקת מיקרו-מערכות |
|---|---|
| מספר קורס | 00350041 |
| עידו פנג בנטוב |
|---|
| CLASSIFIED |
| CLASSIFIED |
חלק א’
נתון משפעל זוויתי בעל אלקטרודה תחתונה מקובעת בזווית
איור HW2.1: סכמה של המשפעל הזוויתי הנתון.
נוסחה לחישוב הקיבול:
שאלה 1
תחת הפעלת מתח
סעיף א’
רשום את האנרגיה הפוטנציאלית הכוללת של המערכת.
פתרון:
האנרגיה הפוטנציאלית של המערכת היא:
לכן:
נחשב את
ולכן:
נציב ב-(HW2.2):
סעיף ב’
מצאו את הכוח הריאקטיבי (גזרו את האנרגיה לפי דרגת החופש).
פתרון:
סעיף ג’
רשמו את תנאי שיווי המשקל.
פתרון:
סעיף ד’
מצאו את קשיחות המערכת.
פתרון:
סעיף ה’
מהי הקשיחות במצב ש”מ. האם יש ערך קריטי בו המערכת מאבדת יציבות?
פתרון:
נחזור לתנאי ש”מ שמצאנו - (HW2.6):
נציב ב-(HW2.7):
או פשוט:
סעיף ו’
מה קורה כאשר
פתרון:
כאשר
TODO: לוודא
שאלה 2
תחת הפעלת מטען
סעיף א’
רשום את האנרגיה הפוטנציאלית הכוללת של המערכת.
פתרון:
האנרגיה הפוטנציאלית של המערכת היא:
ראינו ב-(HW2.3) ש:
נציב ב-(HW2.9):
סעיף ב’
מצאו את הכוח הריאקטיבי (גזרו את האנרגיה לפי דרגת החופש).
פתרון:
נחשב:
סעיף ג’
רשמו את תנאי שיווי המשקל.
פתרון:
סעיף ד’
מצאו את קשיחות המערכת.
פתרון:
סעיף ה’
מהי הקשיחות במצב ש”מ. האם יש ערך קריטי בו המערכת מאבדת יציבות?
פתרון:
קיבלנו כי הקשיחות קבועה וחיובית, ולכן במצב ש”מ המערכת תמיד יציבה.
סעיף ו’
מה קורה כאשר
פתרון:
כאשר
המטען שנמצא על האלקטרודה העליונה מתפרס באופן אחיד עם המטען באלקטרודה התחתונה - כעיקרון יש מגע חשמלי.
שאלה 3
מה הקשר בין התרגיל הזה למשפעל קבל לוחות מקבילי רגיל?
פתרון:
המשפעלים שקולים לחלוטין! קיבלנו את אותם התוצאות, אך פעם מדובר בדרגת חופש קווית, ופעם זוויתית.
שאלה 4
אם לא היינו מתעלמים משדות קצה האם התוצאה הייתה משתנה?
פתרון:
עבור לוחות ארוכים מספיק, התוצאה לא הייתה משתנה - האפקטים של שדות הקצה היו משנים במעט את הערכים המספריים שהתקבלו, אבל הם לא משנים מהותית את
חלק ב’
נתון משפעל לוחות לינארי, כאשר האלקטרודה התחתונה שטחה
יש להניח כי השדה החשמלי בחלק הימני אחיד וניצב לאלקטרודות והשדה החשמלי בחלק השמאלי אחיד וניצב לאלקטרודות.
סכמת המשפעל הנתון.
שאלה 5
כאשר האלקטרודה העליונה נמצאת תחת הפעלת מתח
סעיף א’
רשמו את האנרגיה הפוטנציאלית הכוללת של המערכת.
פתרון:
נוכל להיעזר ב-(HW2.2):
אף הפעם
לכן הקבל השקול:
נקבל:
נציב ב-(HW2.2):
נקבל:
סעיף ב’
מצאו את הכוח הריאקטיבי.
פתרון:
לכן:
סעיף ג’
רשמו את תנאי שיווי המשקל.
פתרון:
סעיף ד’
מצאו את קשיחות המערכת.
פתרון:
לכן:
סעיף ה’
מהי הקשיחות במצב ש”מ? האם יש ערך קריטי בו המערכת מאבדת יציבות?
פתרון:
ננרמל את הגדלים:
כך שמתקבל:
ולכן האנרגיה, הכוח והקשיחות הופכים לפונקציות של
שיווי המשקל מתקבל מ-
והצבה של (HW2.20) בביטוי לקשיחות נותנת:
בגדלים ממדיים נקבל:
חיפוש שורש עבור (HW2.21) נותן
עבור
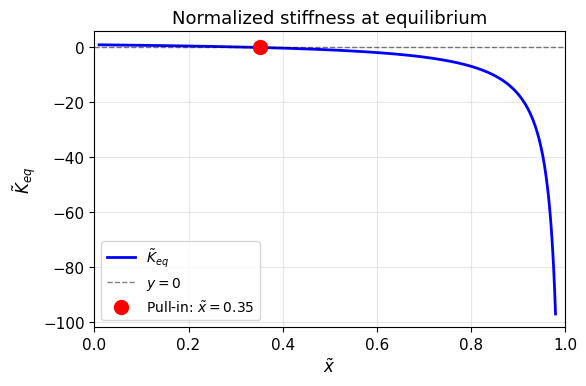
איור HW2.2: הקשיחות המנורמלת
מתאפסת עבור .
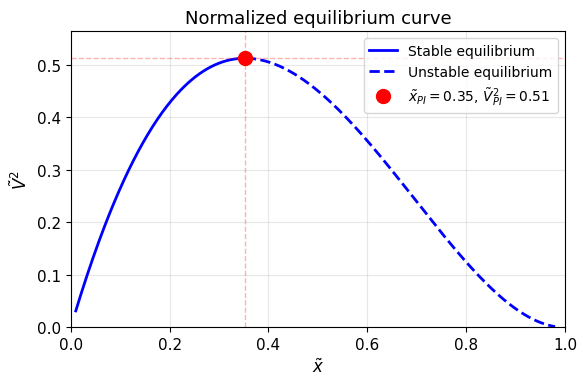
איור HW2.3: עקומת שיווי המשקל
: הקטע המוצק מייצג פתרונות יציבים והמקווקו פתרונות לא יציבים.
שאלה 6
כאשר האלקטרודה העליונה נמצאת תחת הפעלת מטען
סעיף א’
רשמו את האנרגיה הפוטנציאלית הכוללת של המערכת.
פתרון:
ניעזר בביטוי הכללי (HW2.9) עם הקיבול
קיבלנו:
סעיף ב’
מצאו את הכוח הריאקטיבי.
פתרון:
נגזור את (HW2.23) ביחס ל-
ולכן:
סעיף ג’
רשמו את תנאי שיווי המשקל.
פתרון:
סעיף ד’
מצאו את קשיחות המערכת.
פתרון:
ולכן:
סעיף ה’
מהי הקשיחות במצב ש”מ? האם יש ערך קריטי בו המערכת מאבדת יציבות?
פתרון:
נגדיר גדלים מנורמלים:
כמו קודם נקבל:
ומכאן:
משיווי משקל
והצבה בביטוי לקשיחות נותנת:
כך ש-
מתקבל
כלומר, בהפעלת מטען מתקבלת נקודת pull-in בשל אי-אחידות הקיבול.
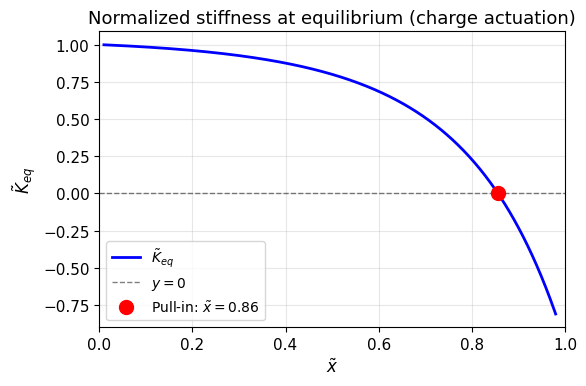
איור HW2.4: הקשיחות המנורמלת
מתאפסת עבור .
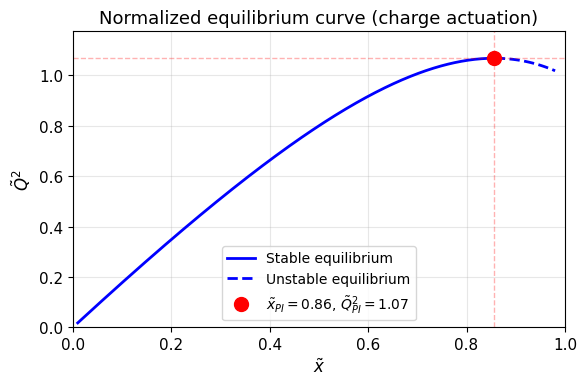
איור HW2.5: עקומת שיווי המשקל
: הקטע המוצק יציב והמקווקו לא יציב.
