NUM1_012 אופטימיזציה

→ קודם: NUM1_011

אופטימיזציה לא מוגבלת

בפרק זה נעסוק במציאת מינימום של פונקציה ב- משתנים. כלומר, עבור פונקציה , ומשתנה , נרצה למצוא את:

לבעיה זו קוראים בעיית מינימיזציה/אופטימיזציה.

דוגמה:

להלן מקרה פשוט בו , , והפונקציה נתונה:

קל לראות שלפונקציה הזאת יש ערך מינימלי בנקודה :

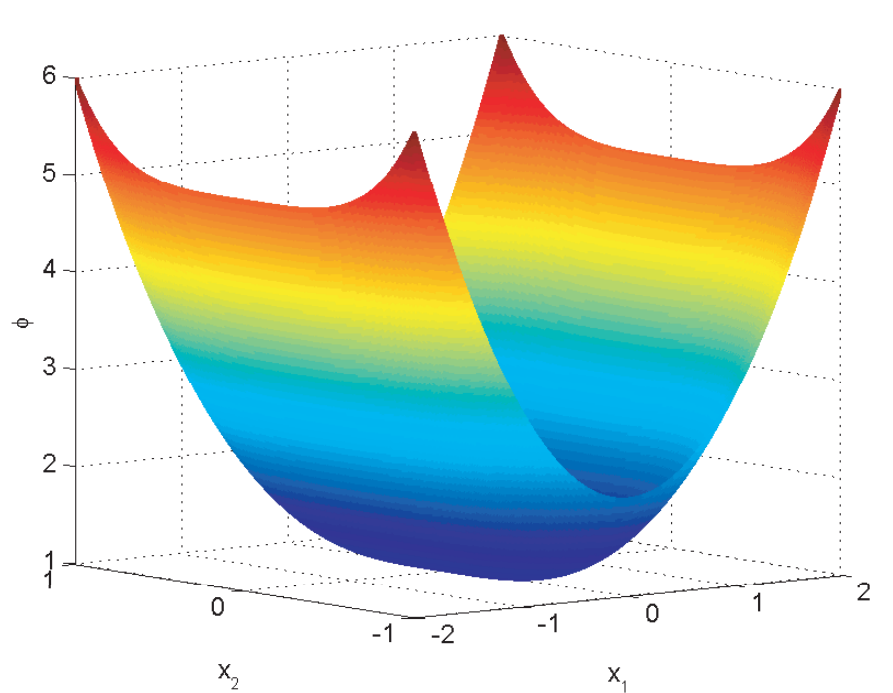
הפונקציה בעלת ערך מינימלי מוחלט בראשית הצירים, ואין לה מקסימום. אם נהפוך אותה, נקבל את הפונקציה . לפונקציה זאת יהיה מקסימום מוחלט בראשית הצירים, ולא יהיה מינימום.

בבעיות אמיתיות ללא פתרון טריוויאלי, אנו לרוב לא יכולים למצוא את הנקודות מינימום רק מלהסתכל על הבעיה. למעשה, לרוב גם לא נדע כמה נקודות מינימום מקומיות יש, ואם הנקודה שהגענו אליה היא בכלל הנקודת מינימום הגלובלית.

כדי לפתור בעיות מינימיזציה, נוכל להמיר אותם לבעיית מערכת משוואות לא לינארית, ומשם לפתור בעזרת שיטת ניוטון. כדי לבצע את המרה זאת, נדרש כמו מקודם לפתח טור טיילור, רק הפעם מסדר :

משפט:

יהי ו-, ונניח כי בעל נגזרות מסדר שלישי לפחות. אזי, לוקטור כיוון , הקירוב טיילור לכל פונקציה בכל רכיב הוא:

כאשר הוא הגרדיאנט של , ו- הוא ההסיין של :

השארית תלויה בנגזרות של מסדר שלישי ומעלה.

פיתוח שיטת ניוטון

נניח של- נגזרת רציפות מסדר שני (). לכן, נוכל לפתח לה את הטור טיילור כפי שראינו מקודם. נזכור מחדו”א 2 שכדי למצוא את המינימום של פונקציה רב משתנית, עלינו למצוא קודם נקודות חשודות, ואז למצוא אם ההסיין בנקודות אילו מוגדר חיובית.

הערה:

שיטת ניוטון כאן רק יודעת למצוא לנו את הנקודות החשודות, אבל היא לא יודעת להבטיח לנו שהנקודות שנמצא הן נקודות מינימום.

כדי למצוא נקודות חשודות, נרצה לפתור את מערכת המשוואות הבאה:

כלומר, אנו מחפשים מתי הנגזרת הראשונה של מתאפסת. את מערכת משוואות זו נוכל לפתור בעזרת שיטת ניוטון למערכת משוואות.

נסמן את ההסיין של ב-:

נשים לב ש- הוא בעצם היעקוביאן של . כלומר ש- . כעת נוכל לרשום את האלגוריתם של שיטת ניוטון במונחים של הבעיית אופטימזציה שלנו:

אלגוריתם: שיטת ניוטון לאופטימיזציה לא מוגבלת

בהינתן בעיית מינימיזציה של מעל , יהי ניחוש התחלתי.
עבור עד שנגיע להתכנסות:

• נפתור כדי למצוא את .
• נציב .

דוגמה:

נביט בפונקציה:

נמצא את הנקודות הקריטיות ע”י המערכת משוואות:

כאשר:

מבחינת הפתרון האנליטי, נקבל שיש לפונקציה מינימום ב- , בו ערך הפונקציה הוא . בנוסף, יש גם נקודת אוכף ב- , כך שגם בו הגרדיאנט מתאפס, ואז .

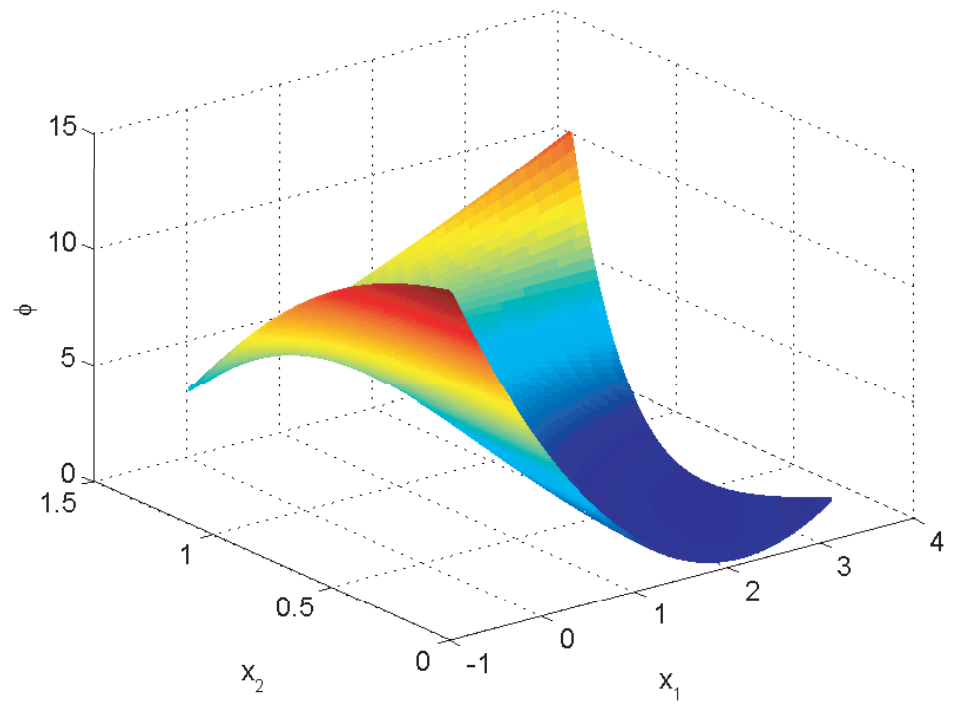
הפונקציה הנתונה בדוגמה. יש לה מינימום ב- וגם נקודת אוכף ב-.

אם נפעיל את שיטת ניוטון עם ניחוש התחלתי , נקבל את האיטרציות עם השגיאות הבאות:

קיבלנו התכנסות יחסית מהירה אל הפתרון .
אם היינו מתחילים מניחוש התחלתי נקבל את האיטרציות עם השגיאות הבאות:

הפעם הפתרון שלנו יתכנס לנקודת אוכף, ולא לנקודת מינימום!

שיטות ירידת גרדיאנט וחזרה לאחור

ראינו מהדוגמה האחרונה שלפתור את בעיית המינימיזציה של פונקציה מסוימת יכולה להיות טיפה בעייתית.
נשים לב שלכל כיוון בנקודה בו הנגזרת לא מתאפסת (, אם קטן מספיק, אז כדי לקבל , נדרש שהנגזרת עצמה תהיה שלילית:

וקטור שמקיים תנאי זה נקרא כיוון ירידה בנקודה . אם חושבים על הפונקציה במובן התלת ממדי (כמשטח), כזה בנקודה מסוימת מתאר את הכיוון בו כדור המונח בנקודה יתגלגל על המשטח (ניזכר בקשר בין גרדיאנט לנגזרת מכוונת מחדו”א 2).

לשיטת ניוטון שראינו יש מספר יתרונות כמו התכנסות ריבועית. אבל, יש לה גם המון חסרונות:

1. נדרש הקיום של ההסיין.
2. נדרש חישוב של ההסיין.
3. נדרש לפתור מערכת משוואות לינארית בכל איטרציה.
4. לא ניתן לדעת אם השיטה תתכנס בכלל לנקודת מינימום, מקסימום או אפילו אוכף.

נביט בשיטה הבאה לטיפול בחסרונות אלו:

ירידת גרדיאנט (gradient descent)

במקום לפתור את המערכת משוואות כדי למצוא את , נבחר במקום זאת את להיות:

בחירת זה מבטיחה שנתקדם בכיוון הירידה. בנוסף, נמנעו מלפתור מערכת משוואות לינארית!
מצד שני, אנו נאלצים לבחור גודל צעד . מעבר לכך, שיטה זו מתכנסת מאוד לאט.

חיפוש קווי וחזרה לאחור

שיטות חיפוש קווי (line search) הן שיטות המתייחסות למציאת גודל צעד מתאים עבור העדכון של האיטרציה שלנו:

בשיטת ניוטון עבור מערכת משוואות לא לינאריות, מאחורי הקלעים כבר בחרנו . הבעיה, שאנו לא בהכרח נוכל לדעת האם עם בחירה זו השיטה שלנו תתכנס.
לפיכך, בהינתן וכיוון ירידה , אנו נחפש לאורך הקו את הערך עבורו מתקיים:

כאשר הוא קבוע שנותן לנו את תנאי העצירה, למשל . בדרך כלל, נתחיל מערך מקסימלי כלשהו, וננמיך אותו אם יש צורך.
שיטה פשוטה הנקראת חזרה לאחור (backtracking) היא לבדוק את השיפור שלנו בין בחירת -ות שונות:

נעצור כאשר קיבלנו את התנאי עצירה לעיל.

---

תרגיל:
חברת חלב רוצה לייצר חמאה. היא רוצה לדעת מהו המחיר האופטימלי שיאפשר לה להרוויח הכי הרבה. החברה חושבת שהיא יכולה לייצר יחידות למחיר הבא:

בנוסף, לאחר סקר שוק, הם מצאו את הנוסחה הבאה שמייצגת את הביקוש כתלות המחיר :

לכן, כמות החמאה שהם יכולים למכור היא , וההכנסה שלהם תהיה:

לבסוף, החברה יכולה לבנות את פונקציית הרווח:

בעזרת ירידת גרדיאנט, מצאו את המחיר האופטימלי. התחילו מ- ובצעו איטרציות עבור צעד קבוע:

איזה צעד מתכנס הכי מהר לפתרון?

פתרון:
נרצה למקסמם את הרווח, ולכן נשים מינוס על הפונקציה, כך שנהפוך את הבעיה למציאת מינימום של הפונקציה:

נמצא כי הגרדיאנט של הפונקציה:

הכיוון שלנו הוא . נציב בביטוי שלנו עבור :

עבור :

באותו אופן עבור ה--ות האחרות, נקבל אחרי איטרציות:

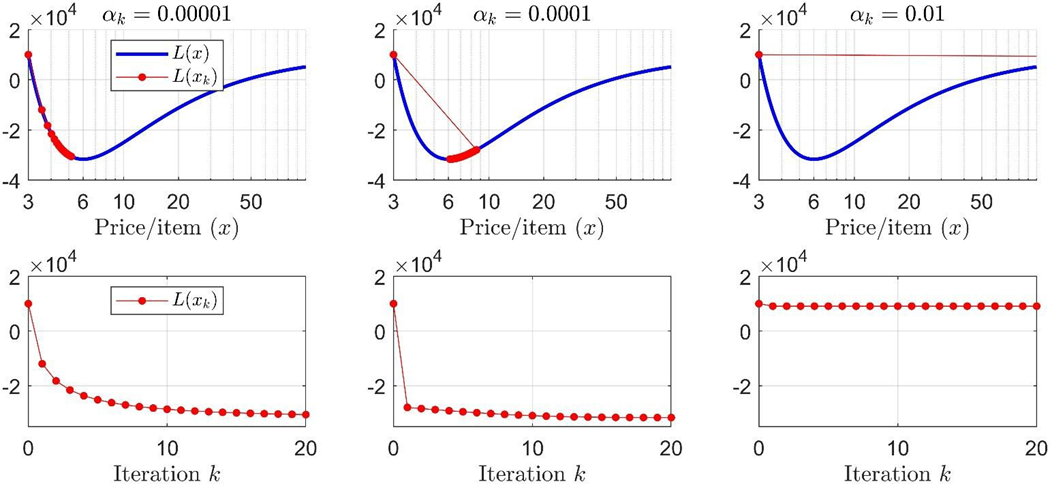
עבור שני הצעדים הקטנים, השיטה מתכנסת למינימום של פונקציית המחיר, - כלומר המקסימום של הרווח.
עם השיטה קודם “קופצת” מעבר לפתרון, אבל היא עדיין מתכנסת יותר מהר מהשיטה עם . לעומת זאת, אנו רואים שעבור השיטה לא מתכנסת.
לסיכום, אפשר לומר שהשיטה מתכנסת הכי מהר עבור .

---

→ קודם: NUM1_011