שיטת ניוטון למערכת משוואות לא לינאריות
נביט במערכת של
כאשר:
בכתיב אינקדסי:
זוהי הכללה של המקרה:
דוגמה:
יהיו
ו- שתי פונקציות המקיימות: המשוואה
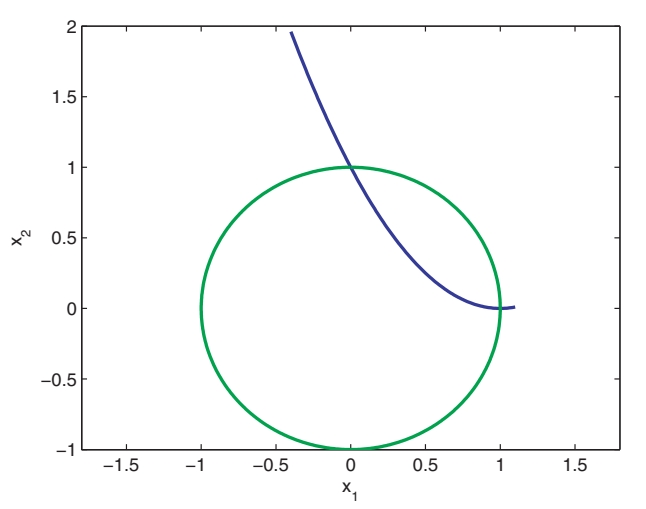
מתארת פרבולה, והמשוואה מתארת עיגול:
ישנם שורשים למערכת המשוואות:שורשים אלה הם נקודות החיתוך
ו-
נניח של-
נתחיל מניחוש
מערכת משוואות לא לינאריות יכולות להיות הרבה יותר מסובכות לפתרון מאשר משוואה לא לינארית אחת במשתנה אחד. בכל זאת, הרבה שיטות כמו שיטת ניוטון, ניתנות להכללה למקרה שאנו עוסקים בו.
הבעיה היא ששיטת ניוטון המוכללת תעבוד לנו עבור
טור טיילור לפונקציות וקטוריות
כדי להתחיל בהכללה לשיטת ניוטון, נצטרך הכללה לטור טיילור, כאשר נשים לב שאנחנו נעסוק במקרה בו
ניזכר בטיילור בשני משתנים. נוכל להכליל אותו עוד יותר עבור מערכת עם
משפט:
יהי
ו- , ונניח כי בעל נגזרות מסדר שני לפחות. אזי, לוקטור כיוון , הקירוב טיילור לכל פונקציה בכל רכיב היא: כאשר
הוא היעקוביאן של : לכן, נקבל בכתיב אינדקסי:
נשים לב שלא רשמנו את הביטוי לשארית החלק מהנגזרת השנייה, ופשוט הסתפקנו בקיצור
כדי לקבל טיפה יותר אינטואיציה לנוסחה שרשמנו, נצייר את
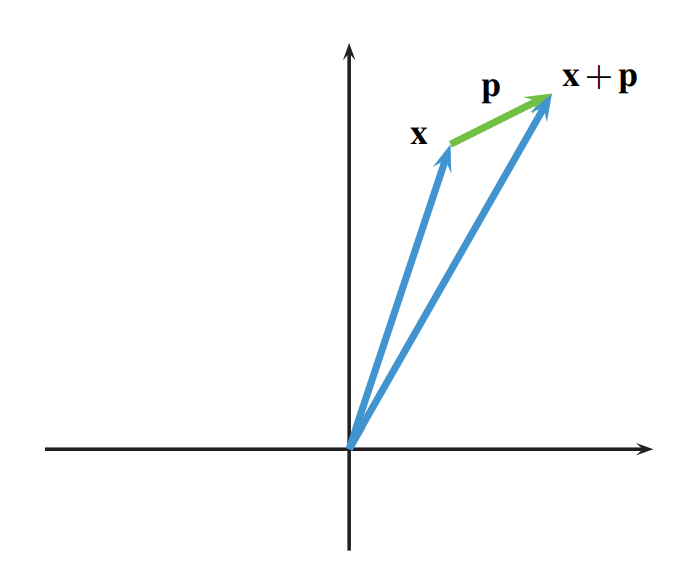
פיתוח טיילור שרשמנו נותן לנו קירוב יחסית די טוב למהו ערך
פיתוח שיטת ניוטון
נחזור למערכת משוואות לא לינאריות:
נתחיל מניחוש התחלתי
ברור שאנחנו לא יודעים מהו
לפיכך, נקבל את האלגוריתם הבא:
אלגוריתם: שיטת ניוטון למערכת משוואות לא לינאריות
עבור
- נפתור
- נציב
ב-MATLAB:
% function [x,k] = newtons(f,x,tol,nmax)
%
% This function returns in x a column vector x_k such that
% || x_k - x_{k-1} || < tol (1 + ||x_k||)
% and in k the number of iterations (Jacobian evaluations) required.
% On entry, x contains an initial guess.
% If k equals nmax then no convergence has been reached.
%
% The iterates ||f(x_k)|| are recorded. This option
% can be easily turned off
function [x,k] = newtons(f,x,tol,nmax)
%Initialize
x = x(:); % ensure x is a column vector
fprintf ('k ||f(x_k)|| \n')
format long g
%Newton
for k=1:nmax
[fx,Jx] = feval(f,x);
fprintf ('%d %e \n',k-1,norm(fx) )
p = -Jx \ fx;
x = x + p;
if norm(p) < tol*(1+norm(x))
fx = feval(f,x);
fprintf ('%d %e \n',k,norm(fx) )
return
end
end
k = nmax;
end