פנגייה

PDE1_004 משוואת הגלים

• זמן קריאה: 18 דק'

משוואת הגלים החד-ממדית

משוואת הגלים ההומוגנית בתחום אינסופי

הגדרה:

משוואת הגלים ההומוגנית החד-ממדית היא:

כאשר הוא קבוע חיובי הנקרא מהירות הגל.

המשתנים הם בעל המשמעות של מרחב, ו- בעל המשמעות של זמן. זוהי משוואה היפרבולית שנוכל לפתור אותה ע”י מעבר לצורתה הקנונית. נגדיר את החילוף משתנים הבא:

לפי כלל השרשרת:

נציב במשוואה ונקבל:

קיבלנו כי הצורה הקנונית היא:

אינטגרציה לפי ואז לפי תביא אותנו לפתרון:

נחזר למשתנים המקוריים כדי שהפתרון הכללי הוא:

כלומר אם הוא פתרון למשוואת הגלים, אז קיימות שתי פונקציות כך שמתקיים המד”ח.
עבור צורת גרף הפונקציה היא כצורת הגרף של , אלא שהגרף מוזז יחידות ימינה. כלומר מתאר גל מתקדם (ימינה) במהירות , ואלו הפונקציה מתארת גל נסוג באותה מהירות. מהירות זו נקראת לכן מהירות הגל.

המשמעות הפיזיקלית של פתרון זה היא ש- הוא סופרפוזיציה של שני גלים, אחד מתקדם ואחד נסוג:
book

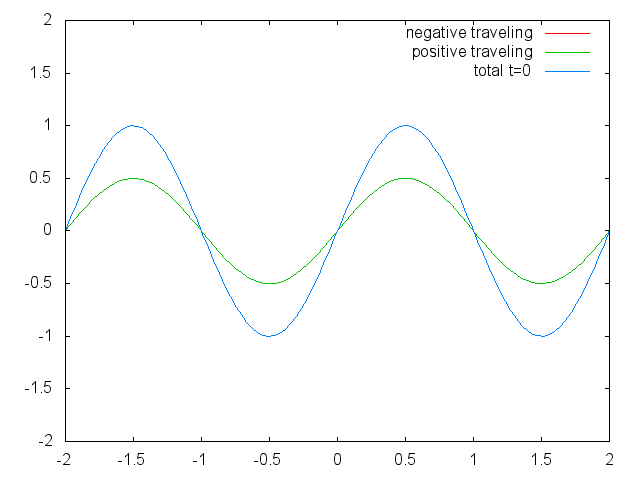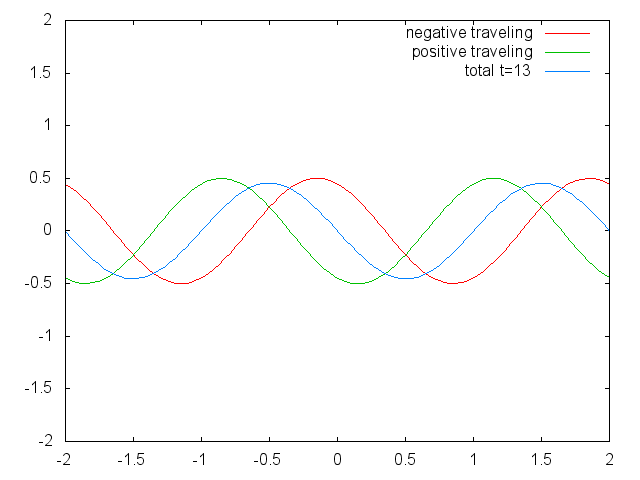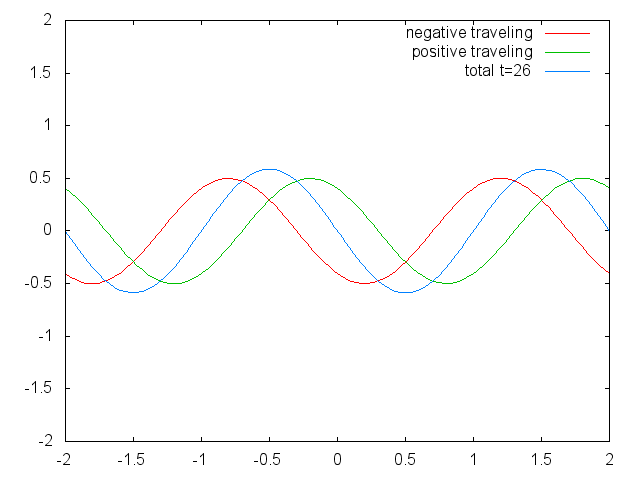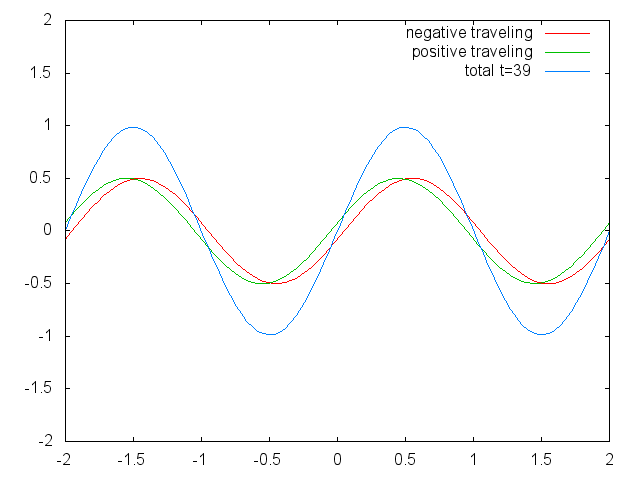
גל חד-ממדי כסופרפוזיציה של שני גלים שמתקדמים בכיוונים שונים.

הערה:

פתרון מצורה זו עבור גזירות פעמיים ברציפות למקוטעין יקרא פתרון מוכלל של משוואת הגלים.

משפחת הקווים האופייניים של משוואת הגלים

הגדרה:

נרכז את מבטינו למישור . שתי משפחות הישרים:

נקראות משפחת הקווים האופייניים של משוואת הגלים. קווים אלו הם קווים ישרים בעלי שיפוע .

נניח כי עבור זמן כלשהו הפתרון הוא פונקציה חלקה פרט לנקודה . ברור אז כי אינה חלקה בנקודה ו/או אינה חלקה בנקודה . מהנקודה הנתונה יוצאים שני קווים אופייניים:

לכן, בכל זמן הפתרון הוא פונקציה חלקה פרט לאחת או שתי הנקודות המקיימות:

כלומר, האי-חלקות מתקדמת אך ורק לאורך קווים אופייניים במהירות הגל . זו תופעה אופיינית למשוואות היפרבוליות, האי חלקות אינה נעלמת והיא מתקדמת במהירות סופית.

דוגמה:

יהי פתרון בכל המישור של משוואת הגלים:

נתון כי קבועה לאורך הישר . עלינו להראות כי .
פתרון:
נציג את הפתרון כסכום של גל נסוג וגל מתקדם:

נתון ולכן:

נסמן ונקבל כי . נציב בחזרה בפתרון הכללי ונקבל:

כאשר “בלענו” את הקבוע ב-. נציב עתה את שמצאנו בשווין שאנו רוצים להוכיח ונקבל:

נוסחת דלמבר

נביט בבעיית קושי הבאה עבור משוואת גלים חד-ממדית בתחום האינסופי:

כדי למצוא פתרון לבעיה, נתחיל מהפיתרון הכללי שמצאנו כבר:

נחפש פונקציות כך שהפתרון יקיים את תנאי ההתחלה. נציב ב- וב-:

אינטגרציה על המשוואה השנייה:

נציב במשוואה הראשונה ונקבל בסוף:

נציב בפתרון הכללי:

נוסחה זו נקראת נוסחת דלמבר.

הערה:

הראינו כי אם קיים פתרון אז הוא נתון ע”י נוסחת דלמבר, ולכן הוא יחיד. ניתן להראות שפתרון דלמבר הוא פתרון אמיתי כאשר , ולכן יש לבעיה זו קיום ויחידות.

תחום התלות

נשוב ונתבונן בבעיית קושי:

אנו מעוניינים לבדוק איזה מידע נדרש כדי לקבוע את הערך של הפתרון בנקודה כלשהי. נרכז את מבטינו למישור . מהנקודה הנתונה יוצאים שני קווים אופייניים

החותכים את ציר ה- בנקודות ו- בהתאמה.

נוצר לנו משולש אשר קודקודיו הם נקודות אלה והנקודה . משולש זה נקרא המשולש האופייני.

מנוסחת דלמבר אנו יכולים להסיק כי ערך הפתרון בנקודה נקבע אך ורק באמצעות ערכי בקודקודי הבסיס האופייני וערכי לאורך הבסיס. כלומר, תלוי רק בערכי ההתחלה הנתונים לאורך הקטע:

הנקרא לכן תחום התלות של הנקודה . שינוי שנבצע בערכי ההתחלה מחוץ לקטע זה לא ישנה את ערך הפתרון .

מבחינה פיזיקלית, אם חושבים על מיתר שכל נקודה בו יכולה לזוז למעלה/למטה, אז אם נתונים לנו הנתונים ההתחלתיים - שהיא מיקום כל נקודה במיתר בהתחלה, ו- שהיא המהירות של כל נקודה בהתחלה, הפתרון שלנו מתאר לנו את המיתר לאורך זמן. אז למשל עבור , לפי תחום התלות, הערך של (הגובה שלו) תלוי בגובה ההתחלתי שלו , ובמהירות ההתחלתית של כל הנקודות בסביבה - שזה נתון ע”י .

עבור כל נקודה בתוך המשולש האופייני, ערך הפתרון נקבע רק ע”פ תנאי ההתחלה הנתונים על (חלק מ-) בסיס המשולש. מכאן נובע שאם תנאי ההתחלה על הבסיס חלקים, אז הפתרון חלק בתוך המשולש האופייני. כלומר:

לא רציפה בכל הנקודות בהן:

בנוסף, לא גזירה בכל הנקודות בהן:

תרגיל:
נתונה הבעיה:

  1. חשב את .
    פתרון:
    לפי נוסחת דלמבר: כאשר .
    נציב:
  2. חשב את .
    פתרון:
    נציב שוב בנוסחת דלמבר: מאחר וכאשר מתקיים: אז נסיק כי: נציב בחזרה ב-(1):
  3. האם הפתרון האמיתי?
    פתרון:
    מאחר ו-, אז הוא פתרון לא אמיתי (פתרון מוכלל).
    נשים לב כי רציפות וגזירות תלוי ב-. במקרה שלנו, אינה רציפה: בנוסף, היא לא גזירה בנקודות אלו מאחר ורציפות הוא תנאי לגזירות.

תרגיל:
נתון:

מצא גל נסוג/מתקדם. שרטט את בזמן . מצא נקודות בהן איזה גזירה.
פתרון:
פתרון כללי של משוואת הגלים:

לפי הפיתוח של דלמבר, הפונקציות נתונות ע”י:

נפרק את האינטגרל שלנו למקרים:

לכן:

כאשר נתעלם מ- כי נראה שהוא יצטמצם לנו.
עכשיו נוכל לשרטט את בזמן :
עבור :

באותו אופן, עבור :

נמצא נקודות בהן איזה גזירה:

נקבל כי:

גם מהגרף וגם מהביטוי ל- ניתן לראות כי לא גזירה כאשר:

משוואת הגלים האי הומוגנית

נתבונן במשוואת גלים אי הומוגנית:

המתארת למשל תנודה של מיתר אינסופי הנתון תחת השפעתו של כוח נתון . כמו במקרה ההומוגני (), תנאי ההתחלה הם פונקציות נתונות המייצגות את משרעת המיתר , ומהירות התנודה בזמן .

נוסחת דלמבר למשוואה אי הומוגנית

כאשר נבצע אינטגרציה כפולה על המד”ח האי הומוגנית, ונפעיל משפט גרין על המשולש האופייני, נקבל שעבור נקודה כלשהי נקבל את הנוסחה הבאה לפתרון הבעיה:

הערה:

ערכי הפתרון בנקודה תלויים בערכי נתוני הבעיה בכל המשולש האופייני שקודקודו העליון בנקודה זו (לעומת רק בסיס המשולש במשוואה הומוגנית). זהו תחום התלות לבעיית קושי האי הומוגנית.

יחידות הבעיה האי הומוגנית

בכל בעיה לינארית, היחידות עבור הבעיה ההומוגנית גוררת את היחידות עבור הבעיה האי-הומוגנית.

טענה:

לבעיית הגלים האי הומוגנית יש לכל היותר פתרון יחיד.

הוכחה:
נניח כי הם פתרונות של בעיית הגלים האי הומוגנית. קל לראות כי הפונקציה פותרת את הבעיה ההומוגנית:

נשים לב כי גם הפונקציה היא פתרון לבעיה הומוגנית זו. לכן, לפי יחידות הפתרון לבעיה ההומוגנית, מתקיים . כלומר, .

אלגוריתם: פתרון בעזרת ניחוש

נוכל לפתור משוואת גלים אי הומוגנית גם בעזרת ניחוש פתרון פרטי:

נניח פתרון פרטי של המשוואה. אז נגדיר:

כעת, נבנה את הבעיה מחדש עבור :

נציב תנאי התחלה:

קיבלנו משוואת גלים הומוגנית.

עכשיו, נותר לנו לפתור את ע”י נוסחת דלמבר למשוואה הומגונית ולמצוא את , כך שנוכל לפתור את המד”ח המקורית:

כדי למצוא פתרון פרטי כלשהו, נראה מספר מקרים:

  1. אם יש לנו מד”ח מהצורה: אז ננחש פתרון מהצורה: למשל, עבור: ננחש ונציב בחזרה במד”ח. מאחר ו- תלוי רק ב- נוכל להגיע לתוצאה:
  2. אם יש לנו מד”ח מהצורה: נציע פתרון: למשל עבור: ננחש , ונקבל כי: ולכן:
  3. אם יש לנו מד”ח מהצורה: נציע פתרון מהצורה: למשל, עבור: ננסה פתרון מהצורה: נציב אותו: זה די מסובך לפתור. אז ננסה: נציב: ונקבל כי: שזהו כבר מד”ר שאנו יודעים לפתור.
    עוד אפשרות היא לנחש פתרון מהצורה: נציב: נקבל כי ואז: והגענו לפתרון הרבה יותר מהר, בלי לפתור מד”ר.

תרגיל:
נזכיר קצת מה זה פונקציות היפרבוליות:

בנוסף:

נתונה הבעיה הבאה:

פתרון:
נשים לב כי פתרון המד”ח הוא מהצורה:

אז ננחש פתרון פרטי מהצורה:

נציב:

כעת, עלינו למצוא את הפתרון של החלק ההומוגני, אז נגדיר:

ולכן:

נציב את התנאי הראשון שלנו:

נציב בנוסחת דלמבר:

לכן הפתרון הוא:

פתרון לפי נוסחת דלמבר למשוואה אי הומוגניות:

משוואת הגלים בתחום חצי אינסופי

בהינתן משואת גלים אי הומוגנית בתחום חצי אינסופי, אנחנו נצטרך עוד תנאי שפה. אז למשל עם תנאי דיריכלה:

כדי לפתור בעיות מסוג זה ניעזר בטענה הבאה, שנובעת מנוסחת דלמבר:

טענה:

  1. אם הן פונקציות אי זוגיות לפי אז גם הפתרון של משוואת הגלים בתחום חצי אינסופי הוא פונקציה אי-זוגית לפי .
  2. באותו אופן, אם זוגיות זוגית.
  3. באותו אופן, אם מחזוריות מחזורית.

נעשה את השלבים הבאים:
ננסח בעיה שקולה עבור , כדי שהתנאי שפה האחרון ייתאפס:

נגדיר הרחבה אי זוגית של במשתנה :

וכעת נפתור כמו בעיה בתחום אינסופי, כדי לקבל פתרון עבור . לפי הטענה, מאחר ו- אי זוגיים לפי , גם אי זוגי לפי . אם היינו מנסים לפתור את הבעיה המקורית בלי להמיר אותה ל-, היינו מקבלים כאן סתירה כי בפונקציה אי זוגית חייב להתקיים . כלומר, זוהי הסיבה למה המרנו לבעיה עם שבה תנאי השפה האחרון מתאפס.

כעת, נותר להציב בחזרה את כדי לקבל את , ולצמצם את הפתרון לחצי המישור:

תרגיל:
פתרו את הבעיה הבאה:

נגדיר תיקון למשוואה, כך שיהיה לנו תנאי בסוף שמתאפס:

נגזור אותו:

ולכן הבעיה החדשה שלנו:

כעת נבצע הרחבה אי-זוגית:

לאחר ההרחבה, הבעיה שלנו נראית כך:

נפתור בעזרת דלמבר למשוואה אי הומוגנית:

ואז אחרי שתיאורתית פתרנו את האינטגרל המסובך הזה, נציב בחזרה ב-.

תחום התלות בתחום חצי אינסופי

נרצה לדעת כיצד הפתרון בנקודה תלוי בפונקציות .
לפי הפתרון הסופי שקיבלנו:

נסיק כי:

  • אם :

    הפתרון שקיבלנו נתון ע”י נוסחת דלמבר, אפילו בלי ה-.

  • אם :

    נצטרך כבר להפריד למקרים - לאם בחרנו הרחבה זוגית או הרחבה אי זוגית:

    1. אם ההרחבה אי זוגית:
    2. אם ההרחבה זוגית:

תנאים לאמיתיות הפתרון בתחום חצי אינסופי

נפרק למקרים:

  1. אם עשינו הרחבה אי-זוגית, אז צריך שיתקיים: מאחר ואנחנו רוצים שלא תהיה קפיצה ב-, והפונקציות הינם אי זוגיות, נדרוש גם כי: כאשר את התנאי הוספנו כדי שגם הנגזרת השנייה של תהיה רציפה ב-.
  2. אם עשינו הרחבה זוגית, אז צריך שיתקיים: בנוסף נדרוש גם שלא תהיה קפיצה בנגזרות של :

תרגיל:
פתרו את הבעית נוימן הבאה:

פתרון:
נבצע הרחבה זוגית. נפרק לתחומים:

משוואת הגלים בתחום סופי

נביט במשוואת גלים הומוגנית בתחום סופי:

עם שני התנאי דיריכלה:

דוגמה:

הבעיה הבאה:

היא בעיית משוואת גלים בתחום סופי (וגם הומוגנית).

אלגוריתם : שיטת הפרדת משתנים

נחפש פתרון מהצורה:

כאשר ו- הן פונקציות של משתנה אחד, ו- בהתאמה. בינתיים אנחנו לא מתחשבים בתנאי ההתחלה. כמובן שאאיננו מעוניינים בפתרון הטרוויאלי . כלומר, אנחנו מחפשים פונקציות ו- שאינן פונקציות האפס.

נגזור את הפתרון:

נציב במשוואה ונקבל:

כמו במד”ר, נבצע הפרדת משתנים כך שנקבל:

בצד שמאל יש לנו פונקציה של בלבד, ובצד ימין ישנה פונקציה של בלבד. מאחר ויש שוויון בינהם, והמשתנים הם בלתי תלויים, נסיק כי הם שווים לקבוע כלשהו:

(הוא במינוס מטעמי נוחות).
קיבלנו כאן מערכת משוואות דיפרנציאליות רגילות:

כדי שהפתרון יקיים את תנאי השפה צריך להתקיים:

מכיוון ש- אינו הפתרון הטריוויאלי, נובע כי:

קיבלנו בעיית שטורם-ליוביל (הגדרה יותר כללית תגיע בהמשך):

נחפש ערך שעבורו יש שהוא לא זהותית אפס שפותר את הבעיה. ייקרא ערך עצמי, ו- ייקרא פונקציה עצמית (כן, זה אנלוגי לערך עצמי מאלגברה לינארית).

מפתרון של המד”ר (כמו במד”ר עם מקדמים קבועים), התחשבות בתנאי התחלה, והתעלמות מפתרונות טריוויאליים, נקבל כי:

  1. אם , אז .
  2. אם , אז .
  3. אם , אז .

כאשר הם מספרים ממשיים כלשהם. נדון בכל מקרה לגופו:

ערך עצמי שלילי (): תנאי השפה הראשון גורר ש-, ותנאי השפה גורר ש- .לפיכך, וקיבלנו רק את הפתרון הטריוויאלי. כלומר, במקרה זה אין למערכת ערך עצמי שלילי.

ערך עצמי אפס (): אנו טוענים כי גם אינו ערך עצמי. כפי שראינו, במקרה זה הפתרון הכללי הוא פונקציה לינארית שמתאפסת לכל היותר בנקודה אחת ולכן לא יכולה לקיים את שני תנאי השפה (אלא אם כן , שבו אנחנו לא מעוניינים).

ערך עצמי חיובי (): הפתרון הכללי עבור הוא:

נציב את תנאי השפה ונקבל . תנאי השפה גורר ש- . על כן, כאשר מספר שלם חיובי.
אין צורך לטפל במקרה כי מקבלים את אותם ערכים עצמיים ופונקציות עצמיות. לפיכך, תנאי הכרחי ומספיק ש- הינו ערך עצמי הוא:

הפונקציות העצמיות שלנו:

כאשר הוספנו את הנוטציה כי ישנם מספר פתרונות.

תרגיל:
פתרו את הבעיה:

פתרון:
ננחש פתרון מהצורה:

נציב במשוואה:

נחלק ב- ונקבל:

נשים לב שחילקנו ב-, שזה בעצם . כלומר כביכל איבדנו פתרון אפשרי - הפתרון הטריוויאלי. אבל, אם נציב בתנאי התחלה, נראה כי הוא לא פתרון של הבעיה.

נפתור את הבעיה עבור , כאשר נשים לב כי:

המד”ר שלנו:

מהתנאי שפה של הבעיה, נסיק כי התנאי התחלה על המד”ר:

נרצה למצוא את כל הפתרונות הלא טריוויאלים שלה. נשים לב שלבעית מד”ר זו לא מתקיים מק”י. למעשה, נראה כי לבעיה זו, ישנם אינסוף פתרונות:

עבור שקיבלנו נפתור את הבעיה עבור :

עבור נקבל ש:

עבור :

פולינום אופייני:

ולכן:

קיבלנו זוגות של פונקציות שמכפלתן הן פתרונות לבעיה. הפתרון הכללי יהיה צירוף לינארי של כל הפתרונות:

נציב תנאי התחלה כדי למצוא את :

בעזרת זהות אנו רואים כי:

נבצע השוואות מקדמים ונקבל:

ולכל שאר ה--ים:

נציב את התנאי התחלה השני:

אחרי כמה חישובים כיפיים עם זהויות נקבל ש:

נבצע השוואת מקדמים:

ולכל שאר ה--ים:

לכן הפתרון הפרטי של הבעיה:

עמודים המציינים את העמוד הזה