ממד
ממדים פיזיקליים
| ממד | סימון | יחידה סטנדרטית |
|---|---|---|
| אורך | ||
| מסה | ||
| זמן |
קיצורים
| קיצור | סימון | ערך |
|---|---|---|
חוקים לגבי ממדים פיסיקליים
- בשוויון, בשני האגפים יש את אותם הממדים.
- במכפלה/במנה של גדלים, הגודל שמתקבל הוא בעל ממד שהוא מכפלה/מנה של הממדים המקוריים.
- מותר לחבר/לחסר רק גדלים בעלי אותו ממד.
- פונקציות מתמטיות מוציאות מספר טהור (חסר ממד) והארגומנט שלהן מספר טהור.
דוגמאות:
- עבור המשוואה הבאה, קבע את היחידות של
- מציאת נוסחה לזמן מחזור של מטוטלת מתמטית.
פתרון:
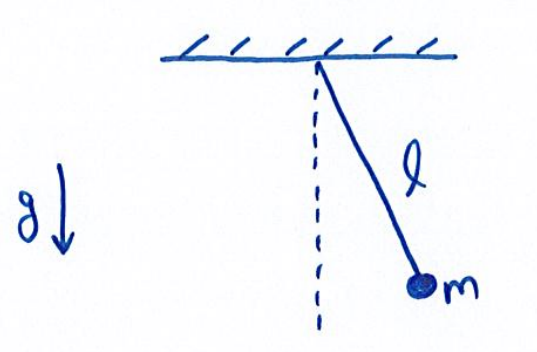
פרמטרים שאולי רלוונטים:
- זווית סטייה התחלתית
- מסה של הכדור
- אורך החוט
- חיכוף עם האוויר
- אלסטיות החוט
- תאוצת הכובד
- מהירות התחלתית
- רדיוס הכדור
- מסה של החוט
מה נוכל להזניח?
נשים לב כי אם באמת נבצע את הניסוי, המטוטלת ממשיכה לנוע גם לאחר זמן רב. אז נזניח את החיכוך עם האוויר. בנוסף, מסת הכדור גם כן גדולה ממש ממסת החוט, ולכן נזניח גם אותה. באותו היגיון נזניח פרמטרים אחרים, ולבסוף נישאר עם: - מסת הכדור -
- אורך החוט -
- תאוצת הכובד -
גדלים פיזיקליים אלו לא בעלי אותו ממד. נוכל להכפילן אחד בשני, או אפילו בעצמן (ואולי להכניסן לפונקציות כמו
הממדים:
נוכל כעת להשוות בין הממדים ונסיק כי:
נפתור ונקבל:
ונסיק כי:
בהמשך נלמד כי אכן:
- עבור המשוואה הבאה, קבע את היחידות של
וקטורים
סימונים:
- וקטור:
- אורך הוקטור:
- שוויון בין וקטורים:
- חיבור וחיסור - חיבור וחיסור וקטורים.
- כפל וקטור בסקלר - כפל וקטור בסקלר.
הערות:
- נשים לב כוקטורי יחידה חסרי ממד:
אבל:
כלומר, וקטור היחידה מתאר את הכיוון בלבד.
נגזרות
סימונים:
לא נשתמש בסימון המקובל לנגזרת -
סימון זה נותן לנו יותר מידע - הוא אומר לנו לפי מה גזרנו את
עבור נגזרת של וקטור:
נגזרת של גודל של וקטור
נבצע “טריק”:
נבצע גזירה לפי כלל השרשרת לאגף הכי שמאלי:
נשווה ונפשט:
קיבלנו כי:
משפט:
יהי וקטור
גזיר לפי . אזי:
