PHY1_002 קינמטיקה

→ קודם: PHY1_001הבא: PHY1_003 ←

קינמטיקה

קינמטיקה - תיאור תנועתם של גופים.

קינמטיקה חד-ממדית

בעולם חד-ממדי, מיקום/העתק של גוף מסוים בזמן נתאר ע”י פונקציה . את המהירות הממוצעת נגדיר ונסמן ע”י:

את המהירות הרגעית:

ולכן מהירות היא נגזרת של מיקום:

תאוצה רגעית:

ולכן תאוצה היא נגזרת של מהירות:

קינמטיקה תלת ממדית

סימונים:
מיקום:
מהירות:
תאוצה:

דוגמאות:

1. גוף נמצא ברגע בנקודה .
   תאוצתו .
   נתון שמהירות הגוף ברגע שניות הייתה . מה מיקום הגוף כתלות ב-?
   פתרון:
   נבצע אינטגרל על כדי לקבל את , ומשם נבצע אינטגרל שוב כדי לקבל את .
   נבצע אינטגרל מסוים:

דרך אחרת להגיע ל היא לחשב אינטגרל לא מסוים, להציב את ולקבל את קבוע האינטגרציה .
כעת נבצע אינטגרל שוב על המהירות, כדי למצוא את המיקום כתלות בזמן:

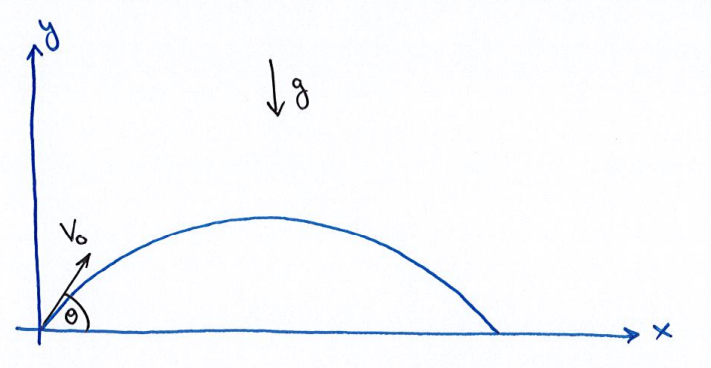
תנועה בליסטית

גוף שנזרק מ- ברגע במהירות שכיוונה בזווית מעל האופק על פני כדה”א (כלומר, תאוצת הכבידה היא ).

• מהו טווח הזריקה?
  פתרון:
  
  נדרוש ש .
  ידוע שהתאוצה בכיוון ציר היא קבועה ושווה ל- (כי בחרנו בציר כלפי מעלה, לעומת הכוח שפועל לכיוון מטה). נסיק כי: כוקטור: נמצא מתי רכיב ה- מתאפס: נציב בחזרה בוקטור את ה- השני שקיבלנו כדי לקבל את טווח הזריקה: נשים לב כי הטווח המקסימלי מתקבל כאשר , כלומר כאשר .
• מהו הגובה המקסימלי אלו מגיע הגוף?
  פתרון:
  נדרוש ש- (שיא הגובה). לכן: נמצא את הגובה המקסימלי ע”י הצבת הזמן ברכיב ה- של המקום:

לסיכום:

נוסחה:

טווח הזריקה:

גובה מקסימלי:

תנועה מעגלית

גוף נע במסלול בעל רדיוס קבוע נגד כיוון השעון.
לתיאור תנועה מעגלית נוח להשתמש בקואורדינטות פולריות (קוטביות):

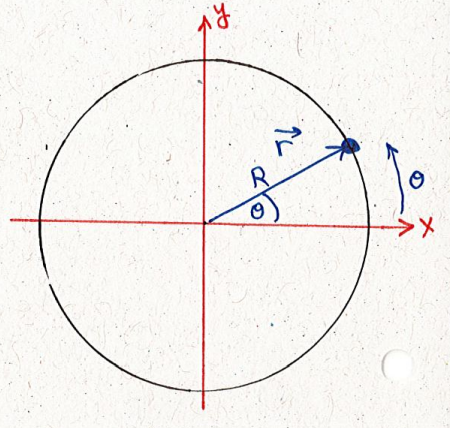
כאשר - הוא המרחק מראשית הצירים, ו- היא הזווית היחסית לכיוון החיובי של ציר ה- נגד כיוון השעון.
תיאור תנועה מעגלית בקואורדינטות קוטביות:

כאשר הוא וקטור יחידה רדיאלי - הוא תלוי בזמן: .

ניתן להמיר ו- נתונים לקואורדינטות :

נמצא את המהירות:

כאשר סימנו , אשר נקרא גם מהירות זוויתית.
קיבלנו כי:

משפט:

בהינתן גוף הנע במסלול בעל רדיוס קבוע ומהירות זוויתית , וקטור המהירות שלו נתון ע”י:

הערות:

1. וקטור היחידה הוא וקטור יחידה רדיאלי.
2. וקטור היחידה הוא וקטור יחידה משיק למעגל, בכיוון החיובי של , כלומר נגד כיוון השעון.
3. הקשר בין ו-:

כי רדיוס לנקודה והמשיק לנקודה במעגל מאונכים זה לזה.
נימוק אלגברי:

5. בתנועה מעגלית תמיד יש תאוצה! המהירות משתנה כל רגע, ולכן בהכרח יש תאוצה:

דוגמאות:

1. האם הביטויים הבאים מתארים תנועה מעגלית?

• הביטוי:

מתקיים ולכן זוהי לא תנועה מעגלית ().

• הביטוי:

נשים לב כי יש לנו את אותה הזווית ואת אותו מקדם ולכן זוהי תנועה מעגלית.

נמצא את התאוצה (הקווית):

חישוב עזר:

נציב בחזרה ב-(1) ונקבל כי:

נוסחה:

הערות:

1. אם המהירות הזוויתית היא קבועה, נשים לב כי זה אומר ש:

בנוסף, לפי , נסיק כי . נציב בנוסחה:

2. את ערך ה- נוכל לחלק לשתי תאוצות:

• תאוצה רדיאלית:

• תאוצה משיקית:

→ קודם: PHY1_001הבא: PHY1_003 ←