DEQ1_007 משוואות לא הומוגניות

→ קודם: DEQ1_006הבא: DEQ1_008 ←

משוואות לא הומוגניות עם מקדמים קבועים

אלגוריתם: שיטת השוואת המקדמים

עבור המד”ר:

נפתור את המשוואה ההומוגנית, ואז כפתרון פרטי, נציע פתרון בצורה הדומה ל- באופן הבא:

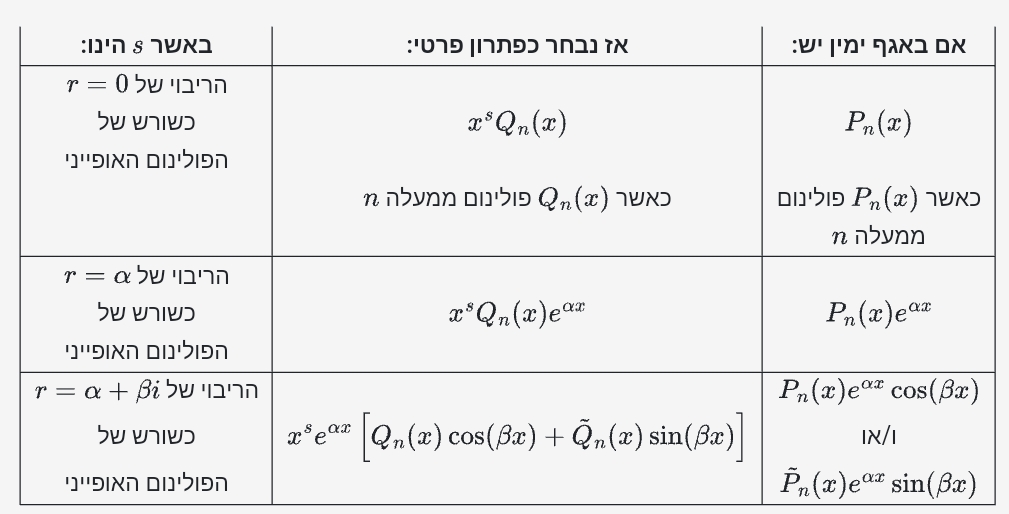
תרגילים:

1. המד”ר:

   פתרון:
   פתרון של החלק ההומוגני:

   ולכן:

   עבור החלק הלא הומוגני, נציע פתרון מהצורה הבאה:

2. המד”ר:

   פתרון:
   נפתור את החלק ההומוגני:

   ולכן:

   נציע פתרון מהצורה:

   נגזור:

   נציב במשוואה המקורית:

   השוואת מקדמים:

   לסיכום, הפתרון הכללי של המד”ר:

3. המד”ר:

   פתרון:
   חלק הומוגני:

   ולכן:

   חלק לא הומוגני:
   נציע פתרון מהצורה:

   נגזור:

   נציב במד”ר:

   נשווה מקדמים:

   קיבלנו:

   לכן הפתרון הכללי:

4. המד”ר:

   פתרון:
   חלק הומוגני:

   ולכן:

   את החלק הלא הומוגני, נפצל לשלושה מקרים. מקרה ראשון:

   נציב במד”ר:

   נשווה מקדמים:

   קיבלנו:

   מקרה שני:

   נציב במד”ר:

   נשווה:

   ולכן:

   מקרה שלישי:

   נציע פתרון:

   נציב במד”ר:

   נקבל:

   נסיק כי:

   הפתרון הכללי:

אלגוריתם: שיטת וריאציית הפרמטר

עבור מד”ר מהצורה:

נמצא פתרון כללי לחלק ההומוגני:

נציע פתרון למד”ר הלא הומוגנית מהצורה:

נפתור את מערכת המשוואות:

תרגילים:

1. המד”ר: בתחום .
   פתרון:
   חלק הומוגני: ולכן: חלק לא הומוגני:
   נציע פתרון: נפתור את המשוואות: נחבר את ו-: כדי למצוא את , ניעזר בכלל קרמר: מתקיים: ולכן בעזרת כלל קרמר: ולכן: אם לא נרצה להשתמש בכלל קרמר, נוכל לעשות פשוט לשחק עם המשוואות כדי לקבל את . נדגים זאת על :
   נכפיל את ב- ואת ב- ונסכום אותם. נקבל: ולכן:

משוואת אויילר

הגדרה:

מד”ר מהצורה:

נקראת משוואת אויילר.

אלגוריתם: פתירת משוואת אויילר הומוגנית

ע”מ לפתור אותה נבצע את הטרנספורמציה:

ואז נוכל לעבור למשוואה עם מקדמים קבועים.
הפתרונות של המשוואה ההומוגונית המתאימה הם כאשר הם שורשי הפ”א. בניית הפ”א האופייני תעשה באופן הבא - עבור ביטוי מהצורה (או הנגזרת ה--ית של ), נציב:

למה? כך ש:

נגדיר פונקציה

ולכן:

ואז כשמציבים בחזרה במד”ר:

קיבלנו מד”ר עם מקדמים קבועים, כאשר הפ”א הוא:

הערות:

1. המעבר בין פתרון של משוואה במקדמים קבועים למשוואת אויילר הוא:

תרגילים:

1. המד”ר: הפ”א: ולכן הפתרון הוא:

אלגוריתם: פתירת אויילר לא הומוגנית

1. פתרון של החלק ההומוגני.
2. נבצע את הטרנספורמציה כך ש-.
   נציע פתרון המתאים ל- מהטבלה של משוואה עם מקדמים קבועים.
3. חוזרים ל-.
4. נציב במשוואה ונמצא את המקדמים של הפתרון הפרטי.

דרך נוספת היא להישאר במשוואה עם מקדמים קבועים. מהפ”א נבנה את החלק עם המקדמים הקבועים של המשוואה.

תרגילים

1. המד”ר: פתרון:
   חלק הומוגני: ולכן: חלק לא הומוגני: נציב פתרון מהצורה: נחזור ל-: נגזור: נציב במשוואה: לכן: ולכן הפתרון הכללי: לפי הדרך הנוספת, כדי לחשב את הפתרון הפרטי היינו יכולים: נציע: נציב במד”ר: ואז היינו חוזרים ל-.
2. המד”ר: פתרון:
   חלק הומוגני: לכן: חלק לא הומוגני: נגזור: נציב במשוואה: ולכן:

→ קודם: DEQ1_006הבא: DEQ1_008 ←