DVI1_007 רטט עקב עירור עצמי

→ קודם: DVI1_006הבא: DVI1_008 ←

מבוא

ראינו שבמערכות מרוסנות, הריסון יכול לעזור למערכת להתכנס לשיווי משקל, ובכך להשיג יציבות. אבל, ישנם מערכות בהם סימן הריסון יכול להיות שלילי, כלומר המערכת תהיה מהצורה:

כאשר .
במקרים אלו המערכת לא יציבה, ואנו קוראים לאי-יציבות מסוג זה רטט עקב עירור עצמי (self excited vibration), או אי-יציבות מסוג פרפור (flutter instability).

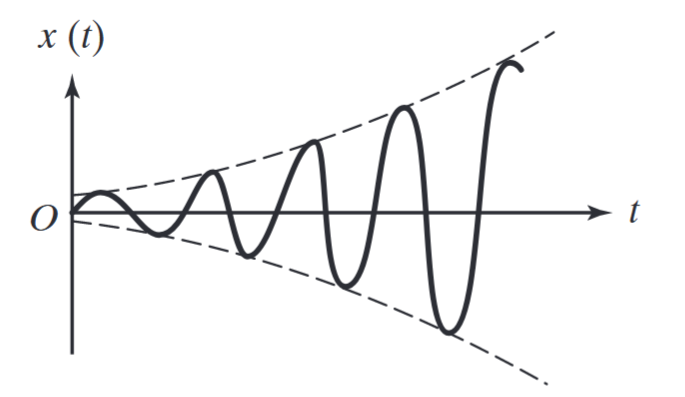
אי-יציבות מסוג פרפור. (Rao, 2018).

ללא עירור חיצוני, כמו ברטט חופשי, נוכל לנחש פתרון מהצורה:

רק הפעם נשים לב שיש לנו באקספוננט ולא , מהסיבה שאנו מכירים בעובדה שהאקספוננט יכול להיות מרוכב. כאשר אנו מציבים את פתרון זה בחזרה במשוואות התנועה, נקבל בעיית ערכים עצמיים:

או למשל במערכת מרובת דרגות חופש:

לביטוי בסוגריים קוראים הפולינום האופייני, ופתרונו (השורשים ) יודע לומר לנו אם המערכת יציבה, ואיך היא יציבה, בדיוק לפי רטט חופשי במערכת בדרגת חופש אחת. שם השתמשנו ב- במקום , אין הבדל ממש במשמעות של הסימון.

פרפור של סכין מחרטה

הערה:

הנושא הבא לקוח מ-(Applied Delay Differential Equations, 2009). לכן הסימונים באיורים שונים מהסימונים שלנו בקורס. במקום זמן מחזור מסומן , ובמקום נרמול בזמן רשום במאמר . נדבוק בסימונים של הקורס עד כה.

מהרגע שהתחילו להשתמש במחרטה מכונאים היו צריכים להתמודד עם בעיית הפרפור של סכין המחרטה:

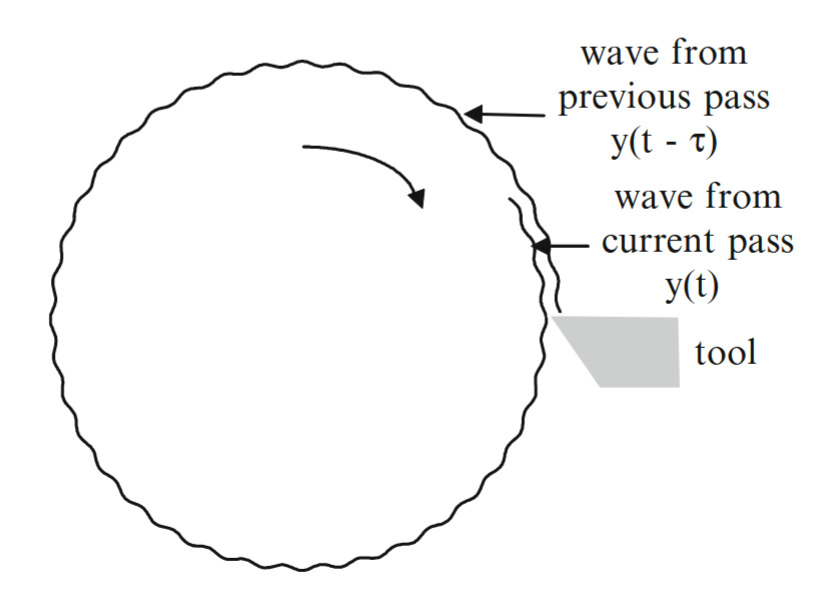
עֻבָּד תחת עיבוד שבבי. הסכין רוטטת כי משטח הדוגמה לא בהכרח ישר בהתחלה, אבל רטט הסכין גורם בעצמו לחיתוך משטח לא ישר. (Applied Delay Differential Equations, 2009).

מהאיור לעיל ניתן להבין שהכוח על הסכין ממשטח העובד תלויה בערך האמיתי, והערך בהשהיה של מיקום הסכין והעובד. ההשהיה שווה בדיוק לזמן המחזור של העובד והוא המקור העיקרי בפרפור פעולת הסכין.

כדי להבין את האי יציבות במערכת, אנו מניחים שהבעיה היא חד ממדית, ושהסכין ניצבת למישור הרצוי לחיתוך.

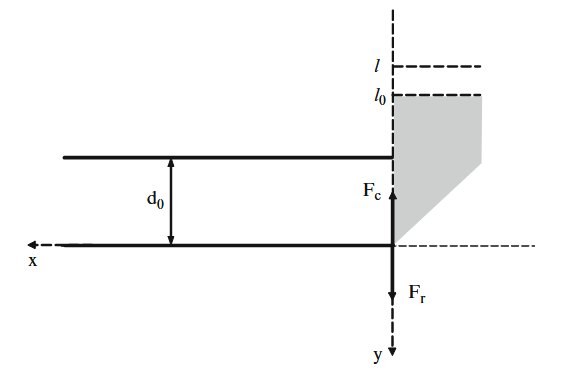
חיתוך במצב מתמיד.

נסמן את מסת הסכין ב-, ואת תכונותיה לחיבור למכונה נתאר ע”י קפיץ וריסון . הערך האפסי של מיקום הסכין מוגרת מוגדר כך שכוח החיתוך נמצא באיזון עם כוח הקפיץ כאשר עובי השבב הוא בדיוק עובי החומר אותו אנו רוצים להוריד, .

כוח הקפיץ של הסכין הוא:

כאשר ו- מתייחסים לאורך ולאורך החופשי של הקפיץ בהתאמה. אנו מניחים שכוח החיתוך הוא פונקציה של עובי השבב בלבד. בחיתוך בשיווי משקל:

משוואות התנועה הן:

בעזרת משוואה (7.100) נוכל לרשום את המשוואה לעיל בצורה הבאה:

נחלק ב-:

כאשר:

כוח החיתוך הוא פונקציה לא לינארית של , ומניסויים נמצא כי:

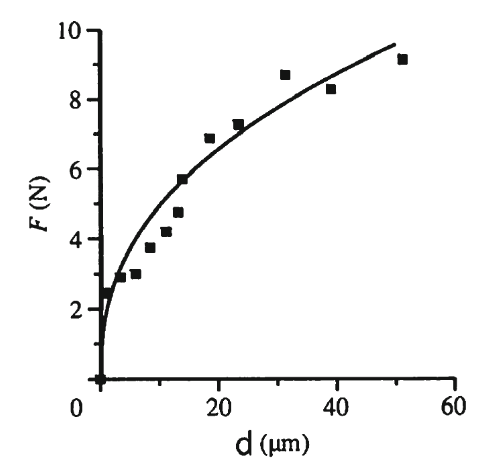
כוח החיתוך בסכין על אלומיניום.

אם ההפרש קטן מספיק, נוכל לבצע קירוב לינארי:

נרצה כעת לקשר בין ו-.

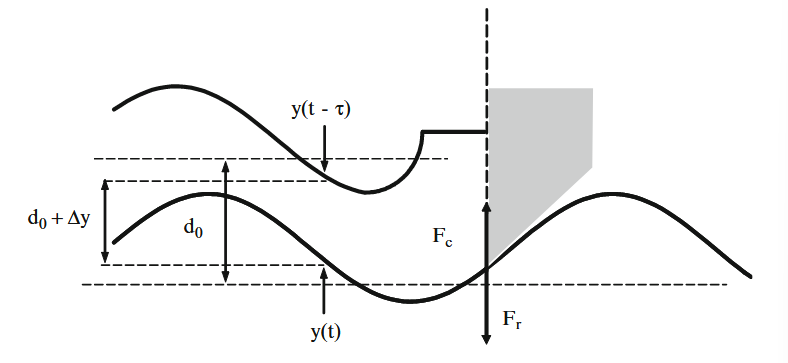
חיתוך עם עובי שבב . במציאות, העובי משתנה עם הזמן והוא פונקציה של המיקום בהווה והמיקום הקודם של הסכין: , כאשר .

כפי שמתואר באיור לעיל:

כאשר ו- הם הזמן מחזור והתדירות הזוויתית של העובד הסובב (במאמר רושמים במקום , ולכן כך משורטט באיורים), בהתאמה. משוואת התנועה שלנו היא כעת:

ננרמל בזמן, :

כאשר:

שוב, הוא זמן המחזור של העובד, לא של הסכין.
נרצה כעת לנתח את יציבות המערכת סביב . נציע פתרון מהצורה . מהצבה ב-(7.109) נקבל את המשוואה האופיינית:

ניתן להראות ש-סף היציבות מתרחש ב- , כאשר . נרצה רק לדעת מהו, או מהם, אלו. נציב במשוואה האופיינית ונקבל:

בעזרת זהויות טריגונומטריות ניתן לפתור את מערכת משוואות זו ולקבל ש:

כאשר . נשים לב שההשהיה (המנורמלת) היא פרופורציונית הפוכה למהירות הזוויתית (המנורמלת) .
משוואות (7.113) ו-(7.116) מספרות פתרון פרמטרי ל- :

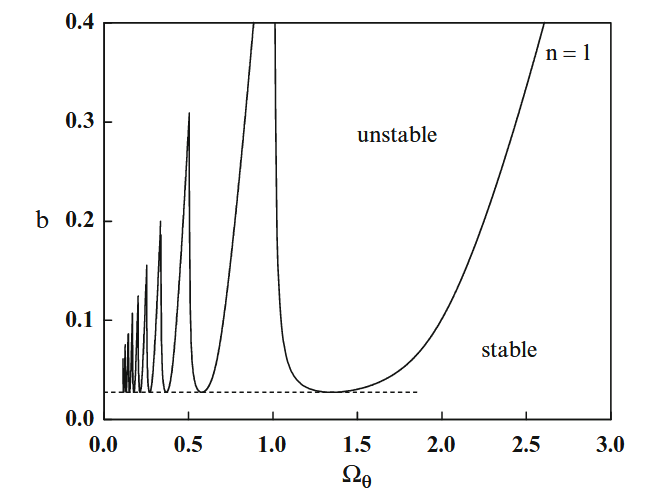
גבולות יציבות המערכת.

כדי להבין מה קורה בגרף זה, נזכור כי:

כאשר הוא התדירות הטבעית של הקפיץ, ו- הוא זמן המחזור של סיבוב העובד. לכן, אם אנו שמים לב לפרפור בסכין, נוכל להעלות את מהירות סיבוב העובד, או שנשנה את הדינמיקה של הסכין (נעלה את התדירות הטבעית , ובכך נוריד את ).

משוואת ריילי ומחזורי גבול

משוואת ריילי (Rayleigh) היא משוואה מהצורה הבאה:

כאשר .
ניתן לחשוב על הריסון בסימן השלילי, , כמקור ש-מכניס אנרגיה למערכת - גורם לה להתבדר. לעומת זאת, על הריסון בסימן החיובי, , ניתן לחשוב כמקור ש-מוציא אנרגיה מהמערכת.
נשים לב שבמהירויות קטנות, הריסון השלילי יותר דומיננטי מהריסון החיובי, ולכן הוא יגרום למערכת להתבדר, ובכך להגביר את המהירות. אבל, במהירויות גבוהות, הריסון החיובי יותר דומיננטי, ויגרום למערכת להתכנס.

את השאר ניתן להבין מהתרגיל.

תרגילים

תרגיל 1

המערכת הבאה מורכבת משני מוטות חסרי מסה ומסות נקודתיות בסוף כל מוט, לכל קצה מוט מחובר קפיץ ומרסן פיתול לינאריים כמתואר באיור. פונקציית הדיסיפציה של ריילי נתונה:

סכמת המערכת. הוא קבוע הריסון פיתול ו- הוא קבוע הקפיץ פיתול.

חקרו את תחומי היציבות וקבע את היציבות עבור המקרה הלא מרוסן.

פתרון:
מיקומי המסות:

לכן המהירות שלהן:

האנרגיה הקינטית:

תחת הנחת זוויות קטנות (שזה תאכלס לינאריזציה סביב ), מתקיים . לכן:

האנרגיה הפוטנציאלית:

לכן הלגראנז’יאן:

את הכוח העוקב על כל חלקיק נוכל לתאר כ:

ולכן הכוחות המוכללים:

נקבל כי משוואות התנועה הן:

ננרמל בעזרת:

לאחר נרמול, כולל נרמול זמן, נקבל:

נעבר למרחב הפאזה - נגדיר וקטור מצב:

והמטריצה:

הפולינום האופייני שלה:

בתרגיל, ביקשו לבדוק את היציבות של המערכת הלא מרוסנת. במקרה זה הפולינום האופייני הוא פשוט:

נסמן . נוכל לרשום:

לפי רטט חופשי אפשר להראות שכאשר התגובה תהיה יציבה, עבור נקבל פרפור, ועבור נקבל התבדרות:

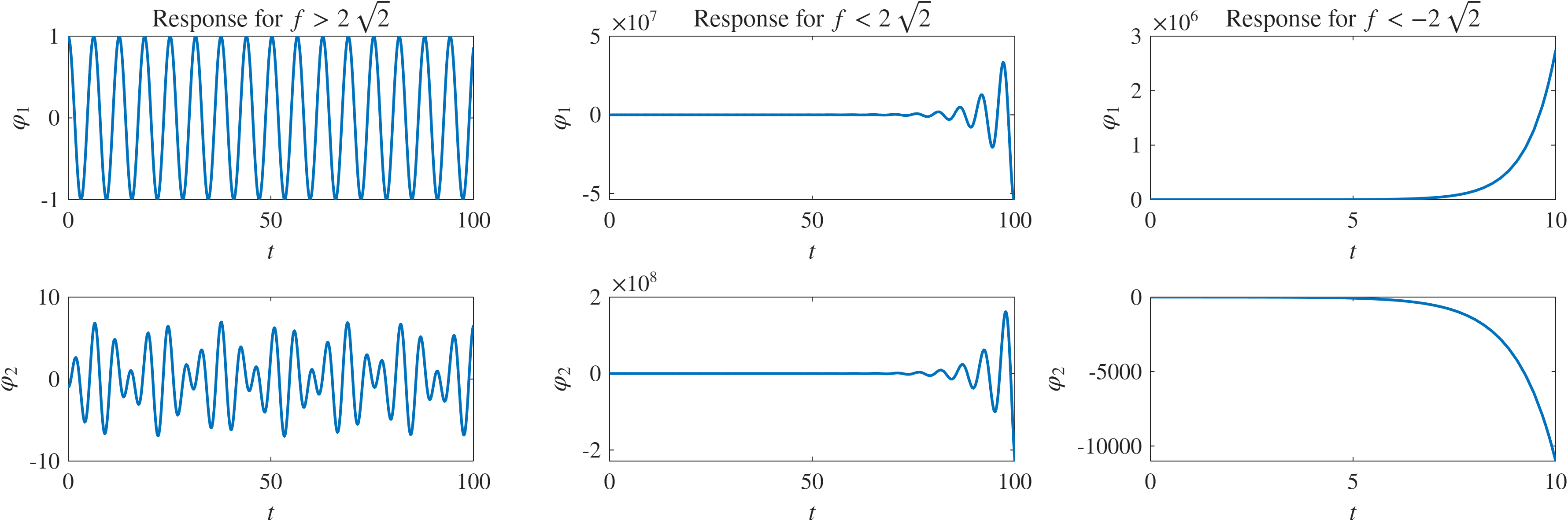
רטט חופשי של המערכת ללא ריסון עבור ערכי שונים.

הקוד לגרף ב-MATLAB נמצא בGitHub.

תרגיל 2

נתונה המערכת הבאה:

מצאו וחקרו את מחזורי הגבול של מערכת.

תזכורת:

על מנת לקבל מחזור גבול (תגובה סטציונרית) נדרוש מאזן בין הכוח שמכניס אנרגיה למערכת לבין האנרגיה שיוצאת בדיסיפציה ע”י הכוח הדיסיפטיבי.

פתרון:
נניח פתרון מהצורה הבאה:

העבודה שעושים הכוחות (הכוח שמבדר והכוח שמכנס אותה):

נבצע הצבה :

נשים לב שהכוח במקרה זה הוא:

נציב באינטגרל ונקבל:

אנו רוצים לדעת מהו סף המעבר בין מעברי האנרגיות, כלומר, אנו רוצים לדעת מתי . כאשר נבצע דרישה זו על הביטוי ל- לעיל נקבל את הפתרון:

כדי לבדוק האם מחזור הגבול שקיבלנו יציב, עלינו לשרטט את האנרגיות שנכנסות ויוצאות מהמערכת כתלות ב- , שהן:

למשל, עבור אנרגיות כלליות:

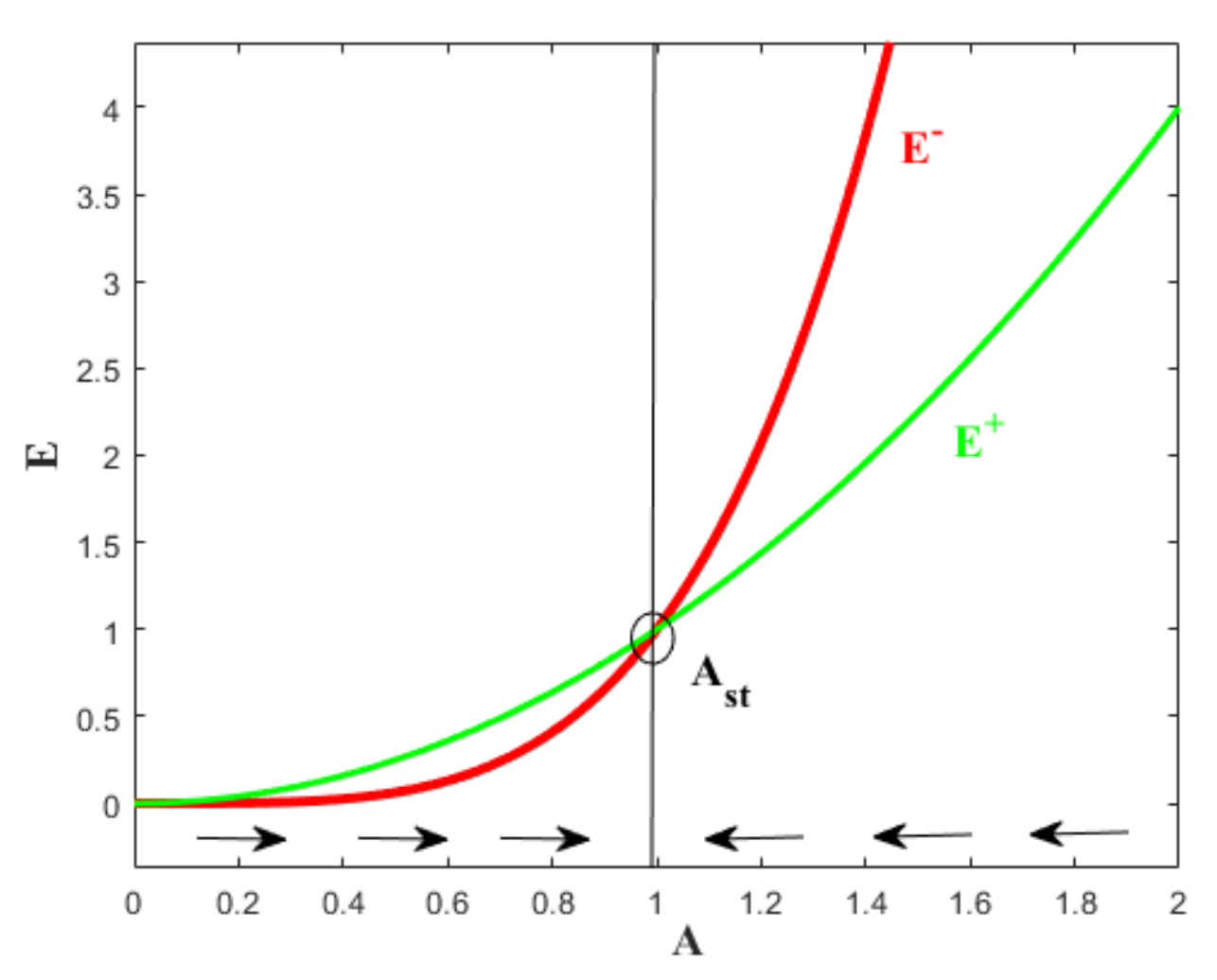
האנרגיות השונות הנכנסות ויוצאות מהמערכת כתלות באמפליטודה.

→ קודם: DVI1_006הבא: DVI1_008 ←