האינטגרל המסוים
הקדמה:
בהינתן פונקציה חיובית קטע
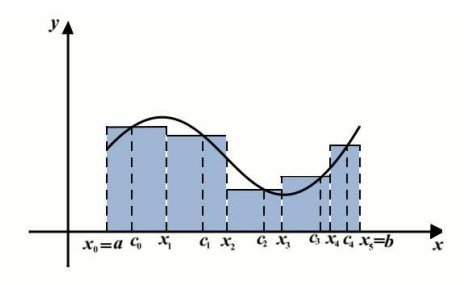
לפי הסימונים בגרף, השטח של כל המלבנים הוא סכומם:
(גובה המלבן נקבע ע”י
ככל שנוסיף עוד
הערות:
- כאשר הפונקציה שלילית, נגדיר את השטח בינה לבין ציר ה-
שלילי.
נניח כיפונקצייה חסומה ב- . חלוקה של היא: שנותן תתי קטעים:
נסמן:
ונסמן:
והוא נקרא הפרמטר של החלוקה
.
ניקח בחירה של נקודות:כלומר ניקח איזשהו
בין .
נרחיב לעוד:
סכום רימן
הגדרה:
סכום רימן (שהוא סכום המלבנים) המתאים לחלוקה
ולבחירת הנקודות הוא:
אינטגרביליות והאינטגרל המסוים
הגדרה:
תהי
פונקצייה חסומה ב- . נאמר כי אינטגרבילית ב- אם קיים מספר כך שלכל קיים כך שלכל חלוקה המקיימת ולכל בחירה של נקודות מתקיים: נסמן:
ערך זה נקרא האינטגרל המסוים של
בקטע .
הערות:
- אם
לכל אז לכל חלוקה ולכל בחירה מתאימה של נקודות: ולכן:
תכונות האינטגרל המסוים
משפט:
- לינאריות: אם
אינטגרביליות ב- אזי גם אינטגריבילית ב- ומתקיים: ולכן:
(למעשה, גם האינטגרל המסוים הוא ט”ל).
2. אדיטיביות: תהיחסומה ב- ויהי . אינטגרבילית ב- אמ”ם אינטגרבילית בקטעים , ובמקרה זה:
- אם
אינטגרביליות ב- אז גם אינטגרבילית ב- . - מונוטוניות: אם
אינטגרביליות בקטע וגם לכל אז:
בפרט, אםלכל אז:
בפרט אםלכל אז והוא מוגדר להיות השטח של: באופן כללי יותר, השטח הכלוא בין הגרפים של שתי פונקציות
מעל קטע הוא:
5. אי שוויון המשולש האינטגרלי:
אםאינטגרבילית ב- אז : לפי סכום רימן:
- נניח כי
מוגדרת ב- פרט למספר סופי של נקודות. נגדיר: כאשר
מוגדרת ב- .
נאמר כיאינטגרבילית ב- ובמקרה זה נגדיר:
למשל:אז אם נגדיר:
ואז נוכל לומר כי:
תנאים לפונקציה אינטגרבילית
משפט:
רציפות למקוטעין
הגדרה:
נאמר כי
רציפה למקוטעין ב- אם קיימות בה מספר סופי של נקודות אי רציפות מסוג סליקה או קפיצה.
המשפט היסודי של החדו”א
פונקצייה צוברת שטח
הגדרה:
תהי
מוגדרת בקטע ואינטגרבילית בכל תת קטע חסום וסגור . ניקח ואז לכל נגדיר: זוהי פונקצייה צוברת שטח.
הערות:
- אם
רציפה בקטע אז היא רציפה בכל ולכן אינטגרבילית ב- .
פונקצייה צוברת שטח רציפה
משפט:
הפונקצייה הצוברת שטח
רציפה בקטע .
הוכחה:
למקרה ש-
הפונקציה
יהי
(לפי אי שוויון המשולש האינטגרלי).
כאשר ב-(1) לפי מונוטוניות האינטגרל.
לכן לפי סנדוויץ’:
שנותן לנו כי:
(כמובן צריך להוכיח גם עבור
מסקנה:
תהי
פונקציה צוברת שטח. אם פונקציות רציפות בקטע , ונגדיר: אז
רציפה בקטע .
הוכחה:
שני הגורמים שקיבלנו בסוף הם רציפים, הרי
דוגמאות:
- מתקיים:
המשפט היסודי של החדו”א
משפט:
נניח כי
מוגדרת בקטע אינטגרבילית בכל תת קטע חסום וסגור של . יהי ונגדיר לכל : אם
רציפה ב- אז גזירה ב- ומתקיים:
הוכחה:
נוכיח עבור
יהי
מכיוון ש-
ניקח
ולכן
ולכן:
כאשר ב-(5) לפי מונוטוניות
לכן,
באותו אופן,
לפונקצייה רציפה יש לפונקציה קדומה
מסקנה:
אם
רציפה ב- אז יש לה פונקציה קדומה של ב- .
תהי. הפונקציה רציפה בכל נקודה, ולכן לכל .
הכללה של המשפט היסודי
מסקנה:
הוכחה:
ראינו כי אם
נוסחת ניוטון-לייבניץ
משפט:
נוסחת ניוטון-לייבניץ: אם
רציפה ב- ו- פונקצייה קדומה של ב- אז: נהוג גם לסמן:
הוכחה:
נגדיר
דוגמאות:
אלגוריתם : אינטגרצייה בחלקים עבור האינטגרל המסוים
נניח כי
הערות:
- אינטגרל לא מסויים:
- אינטגרל מסויים:
וזה נכון כאשר
רציפה. נשים לב כי יש מצבים בהם היא אינה חסומה, ולכן הוא אינו מוגדר.
דוגמאות:
- עבור:
נסמן:
נציב:
אלגוריתם: שיטת ההצבה באינטגרל מסויים
נניח כי
הסבר:
נגדיר
בנוסף:
אז:
הפונקצייה
דוגמאות:
- עבור:
נסמן:
ולכן:
תרגילים:
- חשבו את שטח מעגל היחידה:
פתרון: - הוכיחו כי אינטגרל של פונקציה אינטגרבילית אי זוגית על קטע סימטרי שווה ל-
פתרון:
מתקיים - חשבו:
תרגילים:
- גזרו את
- חשבו את הגבול הבא:
- הוכיחו כי למשוואה הבאה יש לכל היותר פתרון אחד.
- הראו כי:
פתרון: הגבול קיים במובן הרחב.
לכל
לפי מונוטוניות של האינטגרל המסוים:
