מבוא
עד כה עסקנו במערכות בדרגת חופש יחידה, המוגדרות כמערכות שהתנהגותן ניתנות לתיאור ע”י קואורדינטה יחידה. בעוד ישנן מערכות המתאימות לתיאור זה, ועוד הרבה ניתנות לקירוב למערכות כאלו, רוב המערכות צריכות מודל יותר מדויק - מערכות מרובות דרגות חופש.
מערכת לא מרוסנת מסדר ראשון הנתונה לרטט חופשי מגיבה ברטט טבעי, כלומר היא תונדת בתדירות הטבעית שלה. לעומת זאת, במערכות מרובות דרגות חופש, הקיום של רטט חופשי לא רק מעיד על תדירות טבעית מסוימת, אלא גם על תצורת תזוזות טבעית (natural displacement configuration) מסוים של מסות המערכת בזמן תנועה. נרחיב עוד בהמשך.
בנוסף, למערכת מרובת דרגות חופש אין רק תדירות טבעית אחת, אלא מספר סופי שלהם. למעשה, למערכת יש מספר תדירויות עצמיות ותצורות טבעיות, מה שנקרא האופני תנועה (natural modes) של מערכת, כמספר הדרגות חופש שלה. כתלות בעירור ההתחלתי, המערכת יכולה לרטוט בכל אחד מהאופנים האלו עצמאית, בגלל תכונה מיוחדת הנקראת אורתוגונליות.
תצורת המערכת
התנהגות מערכת מרובת דרגות חופש הרבה יותר מסובכת מהתנהגות מערכת בדרגת חופש אחת. כדי לנתח את התנהגותה עלינו להציג עקרונות חדשים. אחת מהשאלות היא איך להציג את תגובת המערכת. במקרה של מערכת בדרגת חופש אחת, הצגנו פשוט את
לכן, עבור מערכות ב-
וקטור זה נקרא הוקטור מצב של המערכת, כאשר
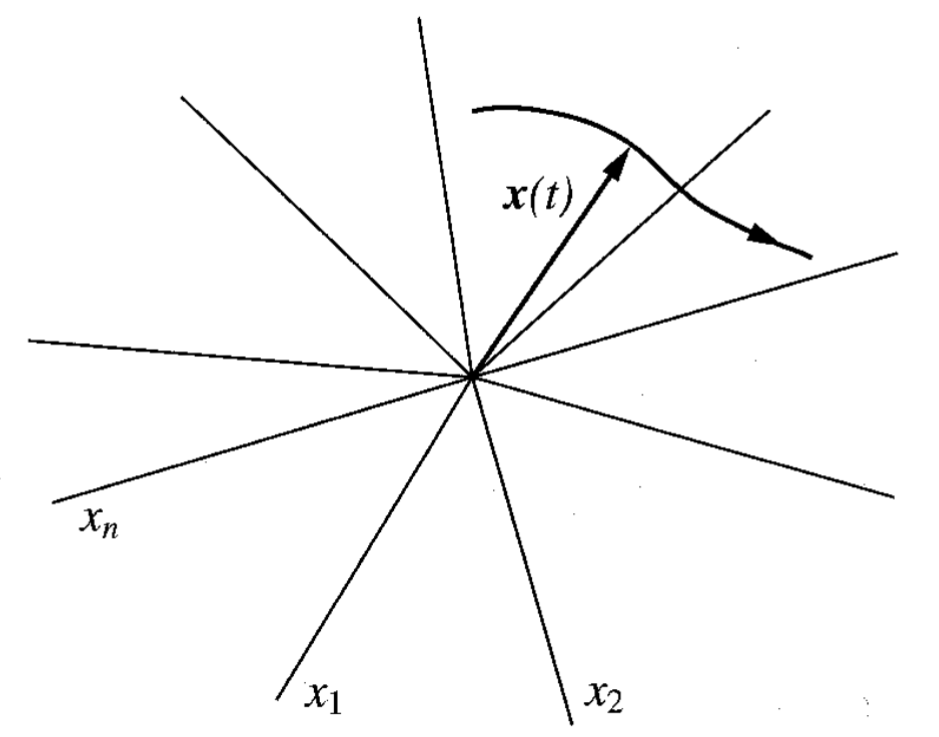
הצגה גאומטרית של התנועה במישור המצב. (Meirovitch, 2001).
הבעיה בייצוג זה שבעוד והיא מעניינת עבור ייצוג כללי של אופן פעולת המערכת, הוא לא מניב שום ערך פרקטי לאפיון המערכת. עוד דרך לייצג את המערכת מובאת לידי ביטוי כאשר נביט למשל במודל של מכונית:
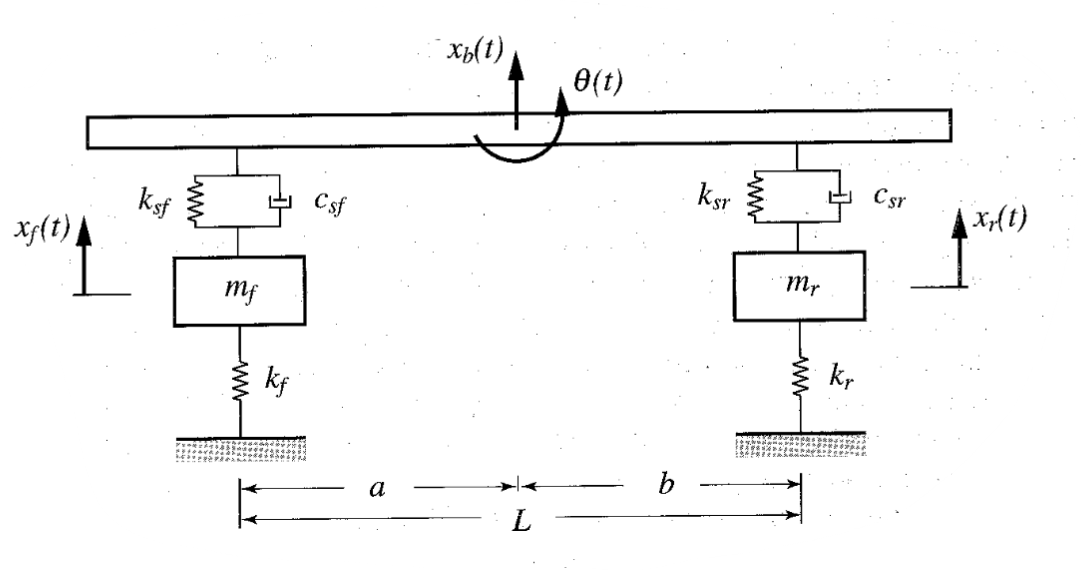
מודל של מכונית. (Meirovitch, 2001).
עבור מערכת זו, נוכל לייצג את וקטור המצב שלנו בעזרת איור מהצורה הבאה:
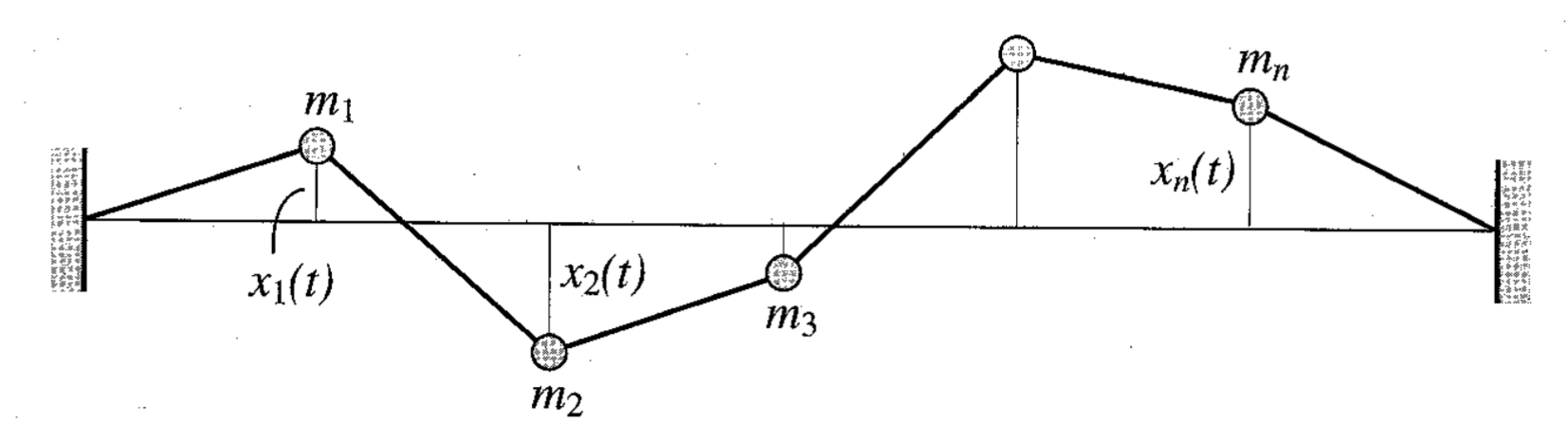
תצורת תזוזות של מערכת ב-
דרגות חופש בזמן כלשהו. (Meirovitch, 2001).
איור זה מתאר דרך הרבה יותר פרקטית לתיאור וקטור המצב
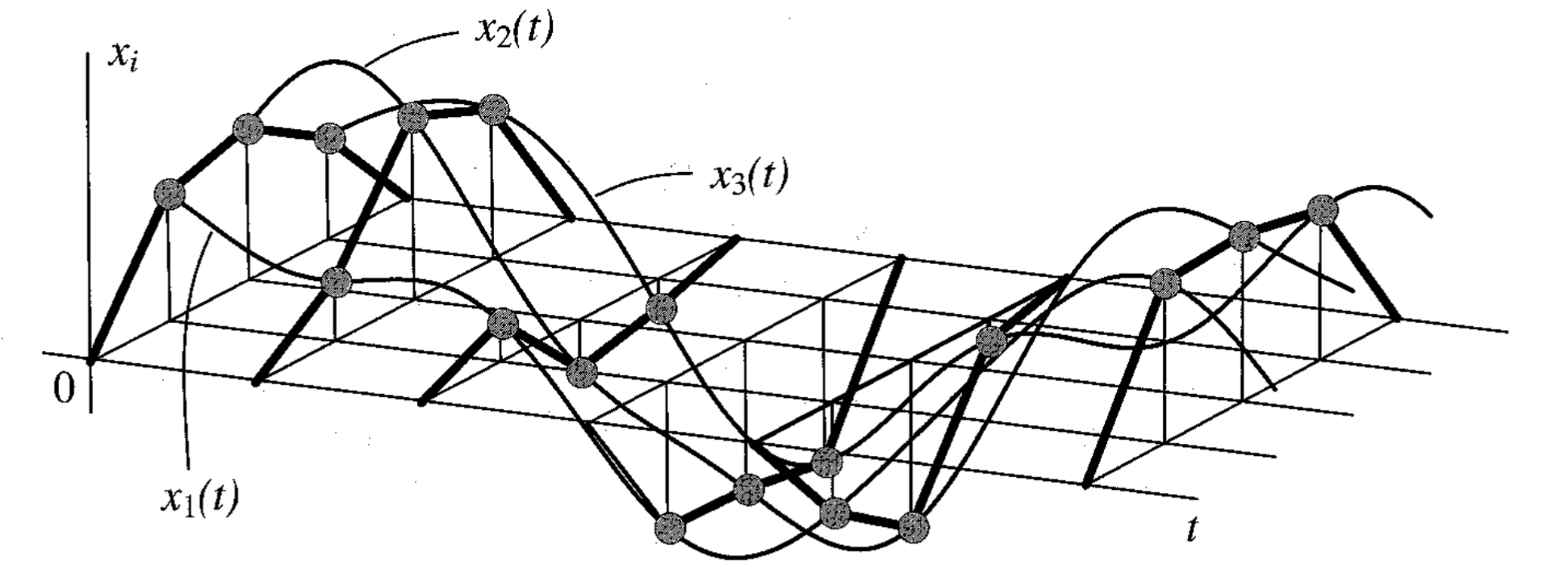
אופן שינוי התצורת תזוזות עם הזמן. (Meirovitch, 2001).
משוואות התנועה של מערכת בשתי דרגות חופש
נציג כעת מספר מערכות בשתי דרגות חופש שונות, נבנה (לא באמת, אין לי כוח להראות את הדרך) את המשוואות תנועה שלהן, ונרשום צורה כללית שלהן שנוכל לאחר מכן לנתח עבור מקרים שונים.
נתחיל ממערכת הכוללת שתי מסות
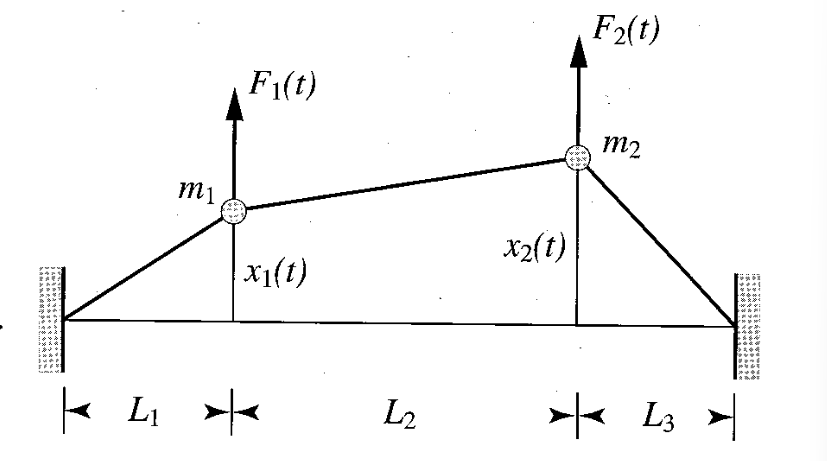
שתי מסות על חוט. (Meirovitch, 2001).
אנו מודדים את התזוזות
עוד מערכת מעניינת היא מערכת של לוח הנתמך ע”י שני קפיצים:
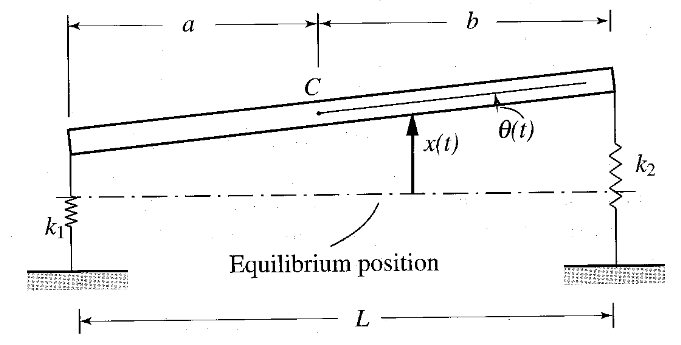
מודל מפושט של מכונית. (Meirovitch, 2001).
משוואות התנועה של מערכת זו:
עבור מערכת המכילה שתי מסות הנתמכות ע”י קפיצים ומרסנים:
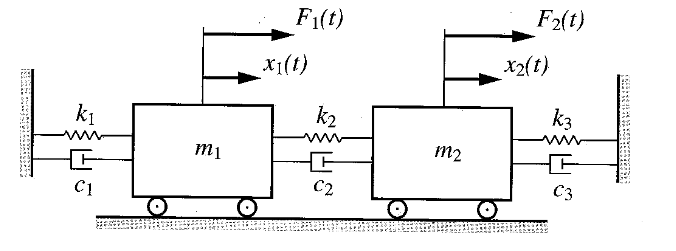
מערכת מרוסנת בשתי דרגות חופש עם ריסון אופקי. (Meirovitch, 2001).
משוואות התנועה:
בפתרון בעיות רטט, חייבים בשלב מסוים לעבור לייצוג מטריצי, ולחזור לאלגברה לינארית, כי אי אפשר בלי. את כל המערכות לעיל ניתן לרשום בכללי בצורה:
למשל עבור (ME5.8), מתקיים:
הנקראים מטריצת הריסון ומטריצת הקשיחות בהתאמה. איכשהו תמיד חוזרים למוצקים 1. המטריצה
והיא נקראת מטריצת המסה, לא יודע למה. הוקטור
רטט חופשי של מערכות לא מרוסנות
בפרק זה אנחנו בעצם מסבירים את ההיגיון מאחורי ניתוח מודלי של מערכת פיזיקליות.
בחקר רטט, יש עניין עצום ב-מערכות משמרות - מערכות שלא פולטות אנרגיה ולא קולטות אנרגיה. המסקנה היא שמערכות משמרות לא נתונות לכוחות מרסנים או כוחות חיצוניים. תחת תנאים אלו, משוואות התנועה של מערכות בשתי דרגות חופש הן:
כאשר
משוואה (ME5.21) מייצגת שתי משוואות דיפרנציאליות רגילות הומוגניות מסדר שני והפתרון שלהן נתון לארבעה תנאי התחלה,
בחקר הרטט מעניינים אותנו פתרונות מיוחדים בהם כל המערכת נעה באותה התנועה בזמן. אנו קוראים לתנועות כאלו תנועות סינכרוניות. המשמעות של תנועה סינכרונית במקרה של מערכות בשתי דרגות חופש לעיל היא שהקואורדינטות
כאשר
מהצבה של (ME5.23) ל-(ME5.21) נקבל:
נכפיל משמאל ב-
כאשר נשים לב ש-
ונקבל:
כאשר נציב את משוואה זו לתוך (ME5.24) נקבל בסוף:
לכן, האמפליטודה התלויה בזמן
ישנן מספר שאלות הנוגעות לטבע וחשיבות התנועות הסינכרוניות. ראשית, קיימת השאלה לגבי סוג התנועות שהמערכת מבצעת בזמן. שנית, כמה תצורות תזוזה יש למערכת?
התשובה לשאלה הראשונה חבויה במשוואה (ME5.27), שהיא משוואת דיפרנציאלית הומוגנית לינארית. לפי משוואה (ME5.26),
כך שנוכל לרשום את (ME5.27) באופן הבא:
נשים לב ש-
כאשר
הקבועים
בכללי, בעיית הערכים העצמיים האלגברית ניתנת לפתירה אך ורק נומרית. היוצא דופן היחיד הוא במקרה של מערכת בשתי דרגות חופש, שבו אנו עוסקים. במקרה זה, המטריצות
משוואות אלו מתארות שתי משוואות הומוגניות עבור ערכים לא ידועים
כאשר
הפתרונות:
שהם למעשה הערכים העצמיים.
נציב את התדירויות במשוואה (ME5.31) ונקבל ש:
כעת כשמצאנו שישנם שתי תנועות הרמוניות סינכרוניות, אחת בתדירות
נציב במשוואה (ME5.32) כדי לקבל:
משוואות (ME5.37) מתארות שתי מערכות משוואות אלגבריות הומוגניות, אחת ל-
היחסים
כאשר
הערה:
בהמשך נסמן את וקטורים אלו עם (
) למעלה, כלומר, נסמן אותם כדי להעיד על כך שהם לא מנורמלים לפי מה שנקרא מסה מודלית, שזהו גם כן מושג שנבקר בהמשך. על כן, בעתיד נקרא לוקטורים אלו וקטורי מודל לא מנורמלים , בעוד לאלה שכן ננרמל נקרא פשוט וקטורי מודל .
התדירות הטבעית
נקבל את התנועות הסינכרוניות כאשר נציב לתוך (ME5.23) את (ME5.36) ו-
שזה תאכלס מה שקיבלנו בניתוח מודלי.
אנו קוראים ל-
כאשר האמפליטודות
תגובה לעירורים התחלתיים
משוואה (ME5.41) מתארת את התגובה החופשית למערכות משמרות בשתי דרגות חופש כקומבינציה לינארית של תנועות טבעיות, המוגדרות כמכפלה של וקטורי המודל
כדי לחשב את התגובה לתנאי התחלה, נצטרך למצוא את ערכי הקבועים
כעת כאשר נציב את תנאים אלו במשוואה (ME5.41), נקבל מערכת משוואות אלגבריות, שנוכל לפתור ואז להציב בחזרה ב-(ME5.41). לטובת תהליך זה, נוח לנו להגדיר את המטריצה המודלית
טרנספורמציית קואורדינטות
משוואות התנועה של מערכת בשתי דרגות חופש משמרת הנתונה ע”י משוואות (ME5.21) מאופיינות בעובדה שמטריצת המסה שלהן אלכסונית, שזה די נפוץ למערכות דינמיות שהקואורדינטות שלהן מתארות את התזוזות של המסות. לעומת זאת, מטריצת הקשיחות לא אלכסונית. אם היא הייתה אלכסונית, שתי משוואות התנועה היו בלתי תלויות, שזהו מקרה אידיאלי כי אז קל יותר לפתור ולהבין אותן. כאשר מטריצת הקשיחות לא אלכסונית, נאמר ששתי המשוואות מצומדות - שינוי בתזוזה של אחת משפיעה על השנייה.
נביט למשל במערכת הבאה:
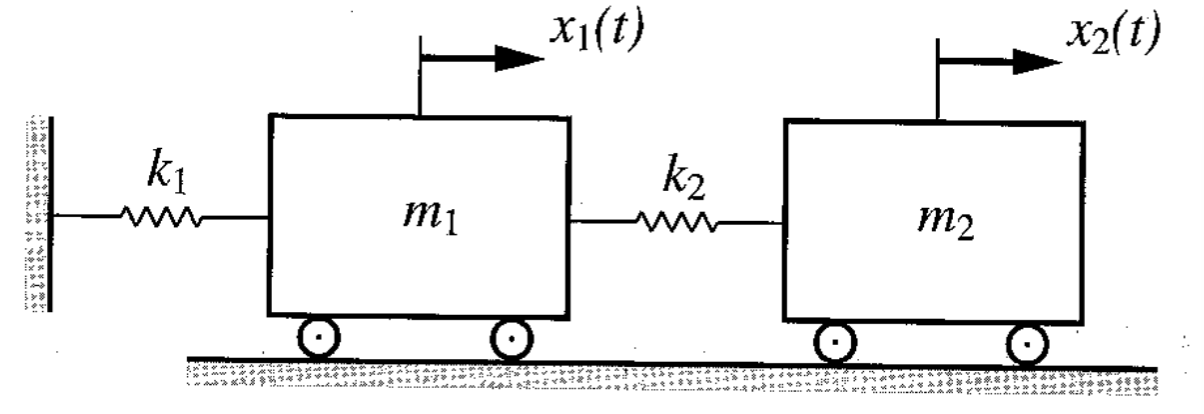
מערכת בשתי דרגות חופש תת-מרוסנת. (Meirovitch, 2001).
משוואות התנועה שלה:
כאשר
כעת נשאלת השאלה האם אנו יכולים ללכסן את
או, בצורה מטריצית:
כאשר:
נפעיל את הטרנספורמציה הזאת על משוואות התנועה:
כאשר:
למקרה זה בו מטריצת המסה לא מלוכסנת ומטריצת הקשיחות כן, אנו קוראים צימוד אינרציאלי, בעוד למקרה ההפוך שהיה לנו בהתחלה אנו קוראים צימוד אלסטי. בשתי מערכות הקואורדינטות לא פשוט לפתור את משוואות התנועה, אבל הראנו עיקרון חשוב - צימוד הוא לא מאפיין של המערכת, אלא של הקואורדינטות בהן השתמשנו כדי לתאר את המערכת. כדי שטרנספורמציית קואורדינטות תעזור לנו לפתור את מערכת המשוואות, עליה להוריד גם את הצימוד האלסטי וגם את הצימוד האינרציאלי. בחלק הבא נדון בטרנספורמציה זו.
אורתוגונליות של מודים
חשיבות וקטורי המודים שהצגנו במשוואות התנועה של מערכת בשתי דרגות חופש, מודגשת כאשר אנו רוצים לפתור משוואות תנועה של מערכות מרובות דרגות חופש. הסיבה לכך היא שלוקטורים המודלים יש תכונה חשובה הנקראת אורתוגונליות. ישנם קבוצות של וקטורים אורתוגונליים, אבל רק רק הוקטורים המודלים אורתוגונליים גם ביחס למטריצת המסה וגם ביחס למטריצת הקשיחות, מה שנקרא בי-אורתוגונליות. כתוצאה מכך, טרנספורמציית קואורדינטות ע”י הוקטורים המודליים יכולה ללכסן את שתי המטריצות.
ממשוואות (ME5.38) ו-(ME5.39), וקטורי המודל של מערכות בשתי דרגות חופש המוגדרת ע”י משוואה (ME5.21) ניתנים לביטוי כ:
כאשר
שהיא סקלר.
אבל, ממשוואה (ME5.35) אנו יכולים גם לרשום:
נציב את (ME5.62) לתוך (ME5.61) ונסיק כי:
משוואה זו קובעת שוקטורי המודלים
כעת, נציב את משוואה (5.29) לתוך-(ME5.28) ונרשום את הפתרונות לבעיית הערכים העצמיים בצורה:
נכפול את שתי המשוואות משמאל ב-
נהוג להציג את הסימונים:
כאשר נשים לב שנוכל עכשיו לרשום:
נרצה גם לעבוד עם וקטורים מודליים מנורמלי מסה
כאשר
הערה:
הסימון
מעיד על כך שמדובר בוקטור/גודל ש-לא מנורמל מסה. ככה שתאכלס עד עכשיו הייתי צריך לרשום על כל .
מה שאומר ש:
כלומר, כל מוד מחלקים ב-
נשים לב ש:
וגם:
לכן נוכל לרשום בכללי, בעזרת הדלתא של קרונקר:
כעת, בעזרת המטריצה המודלית הטבעית אנו יכולים לבצע מעבר בסיס למשוואות התנועה כדי לקבל משוואות תנועה שהן לא מצומדות. אנו עושים זאת בעזרת קואורדינטות מודליות
כלומר, אנו מתארים את הקואורדינטות המוכללות כקומבינציה לינארית של עמודות
נכפיל ב-
נישאר עם:
קיבלנו 2 משוואות לא מצומדות:
ניסוח יותר כללי של משוואות התנועה
הגדרה יותר כללית למטריצת המסה והקשיחות היא (בהנחה והמערכת לינארית):
כאשר
המטריצה
כעת נוכל לרשום את משוואות התנועה באופן:
כאשר
תופעת הפעימות
כאשר שתי מערכות בדרגת חופש אחת מחוברות ע”י קפיץ חלש, המערכת בשתי דרגות חופש המתקבלת מאופיינת בתדירויות טבעיות שמאוד קרובות אחת לשנייה. התגובה של מערכת בשתי דרגות חופש לעירור התחלתי מסוים חווה תופעה מוכרת הידועה בשם תופעת הפעימות (beat phenomenon).
כאשר לתאר את תופעה זו, נביט במערכת המכילה שתי מטוטלות המחוברות בקפיץ, כפי שמוצג באיור הבא:
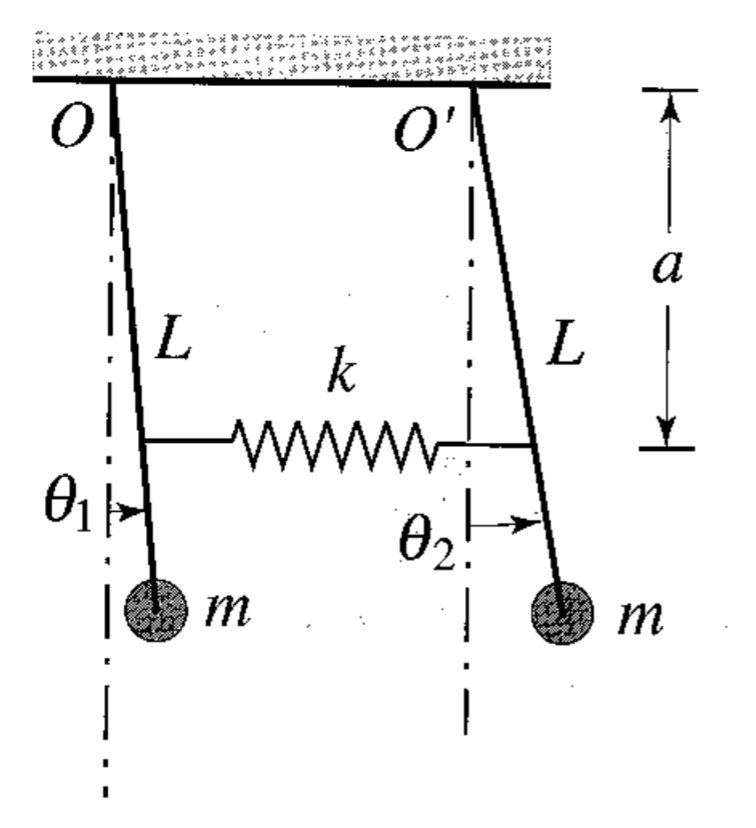
שתי מטוטלות זהות המחוברות בקפיץ. (Meirovitch, 2001).
ללא שום הנחות על קבוע הקפיץ, משוואות התנועה של המערכת הן:
שניתן לסדר בצורה המטריצית:
נשים לב שככל ש-
כעת, נזכור שעבור עירור חופשי תגובת המערכת הרמונית, ולכן נוכל להניח פתרון מהצורה:
כאשר
מה שמוביל למשוואה האופיינית:
ולכן התדירויות הטבעיות הן:
נקבל את המודים הטבעיים ע”י הצבת
כך שבמוד הטבעי הראשון שתי המטוטלות נעות כמטוטלת אחת עם קבוע
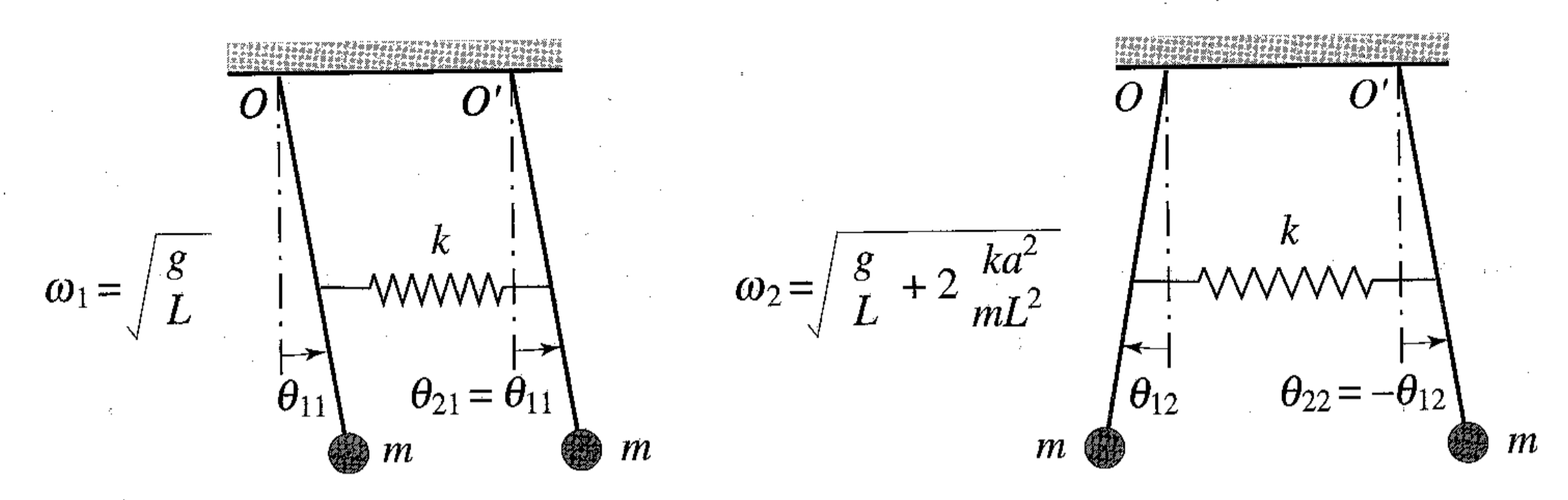
שני המודים הטבעיים של המערכת. (Meirovitch, 2001).
כפי שהוצג באורתוגונליות של מודים, הרטט החופשי של מערכת משמרת בשתי דרגות חופש היא סופרפוזיציה של שני מודים טבעיים המוכפלים בקואורדינטות הטבעיות, או פשוט:
נוכל שרירותית לבחור
אם ניקח למשל את תנאי ההתחלה:
בעזרת זהויות טריגונומטריות נקבל:
בהנחה וקבוע הקפיץ מקיים
נציב ב-(ME5.88):
לכן, במקרה הספציפי הזה, עם תנאי ההתחלה האלו, וקבוע קפיץ חלש זה, נוכל להתייחס לפונקציות
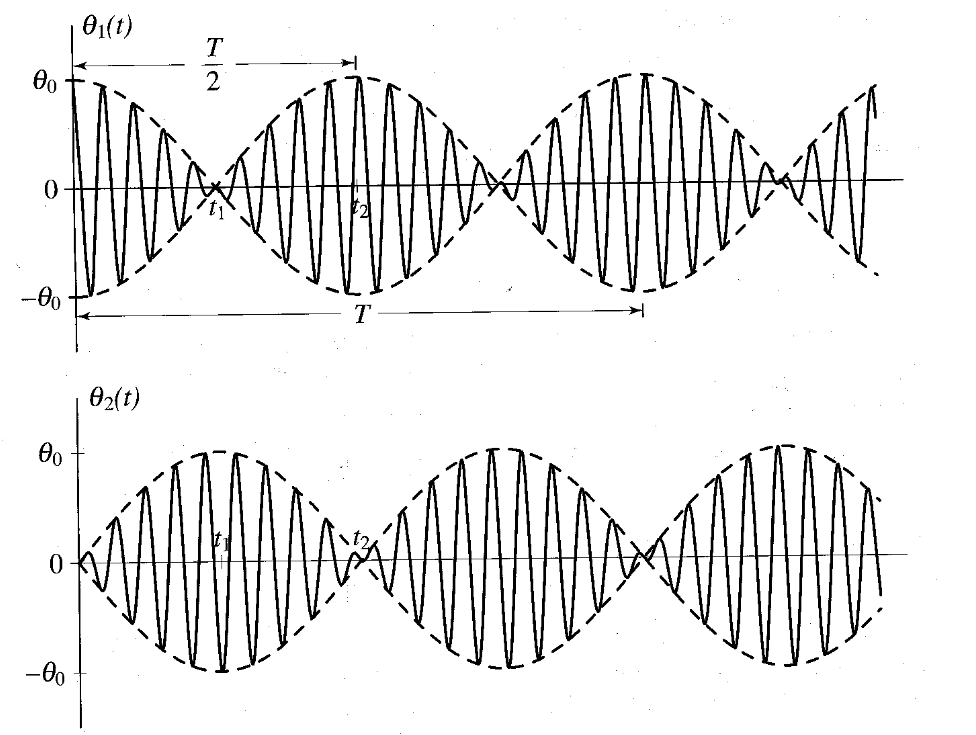
תגובה של המטוטלות - תופעת הפעימות. (Meirovitch, 2001).
עירורים הרמוניים
משוואות התנועה של מערכת בשתי דרגות חופש הן מהצורה:
כאשר:
אנו מעוניינים במקרה שהעירור החיצוני הוא הרמוני. נוכל לרשום את העירור בצורה:
כאשר
כעת, כמו במערכת בדרגת חופש אחת, תגובת המצב מתמיד היא:
בו
כאשר:
היא מטריצת האימפידנס עם הערכים:
הפתרון של (5.96) הוא פשוט העברת אגף של
למטריצה
בהצבת ביטוי זה ל-(ME5.99) נקבל:
במקרה של מערכות לא מרוסנות, פונקציות האימפידנס הן ממשיות:
כאשר נציב אותם לתוך (ME5.101), נקבל:

תגובת תדירות למערכת לא מרוסנת בשתי דרגות חופש. (Meirovitch, 2001).
סופגי רטט לא מרוסנים
כאשר מכונה סובבת פועלת בתדירות הקרובה לרזוננס של הרכיבים המרכיבים אותה, אנו מקבלים רטט עצום כתוצאה מאותו הרזוננס. בהנחה ונוכל לתאר את המערכת בעזרת דרגת חופש אחת הנתונה לעירור הרמוני, נוכל להנמיך את רטט המערכת ע”י שינוי המסה או קבוע הקפיץ. אבל, ישנם מצבים בהם זה לא אפשרי. במקרים אלו, ניתן להוסיף עוד מסה וקפיץ למערכת, כאשר המסה הנוספת והקפיץ מתוכננים כך שהם יוצרים מערכת בשתי דרגות חופש שתגובת התדירות שלה היא אפס בתדירות העירור. נשים לב בגרף לעיל שתגובת תדירות שההגבר שלה הוא אפס באמת קיים. למערכת בשתי דרגות חופש החדשה יש שתי תדירויות רזוננס, אבל תדירויות אלו לא מהוות בעיה כי הן יהיו מספיק רחוקות מתדירות העירור.
נתאר את המערכת החדשה בעזרת שתי מסות וקפיצים, כפי שמוצג באיור הבא:
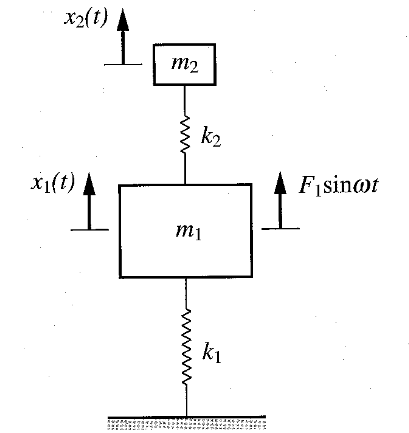
סופג רטט. (Meirovitch, 2001).
כאשר
משוואות התנועה של המערכת לעיל הן:
נשים לב שמכיוון שהמערכת לא מרוסנת, לא נצטרך להשתמש בסימונים מרוכבים, והפתרון יהיה פשוט:
בעזרת החלק הקודם, נוכל למצוא את
בעוד סופג רטט מתוכנן לספוג תדירות מסוימת
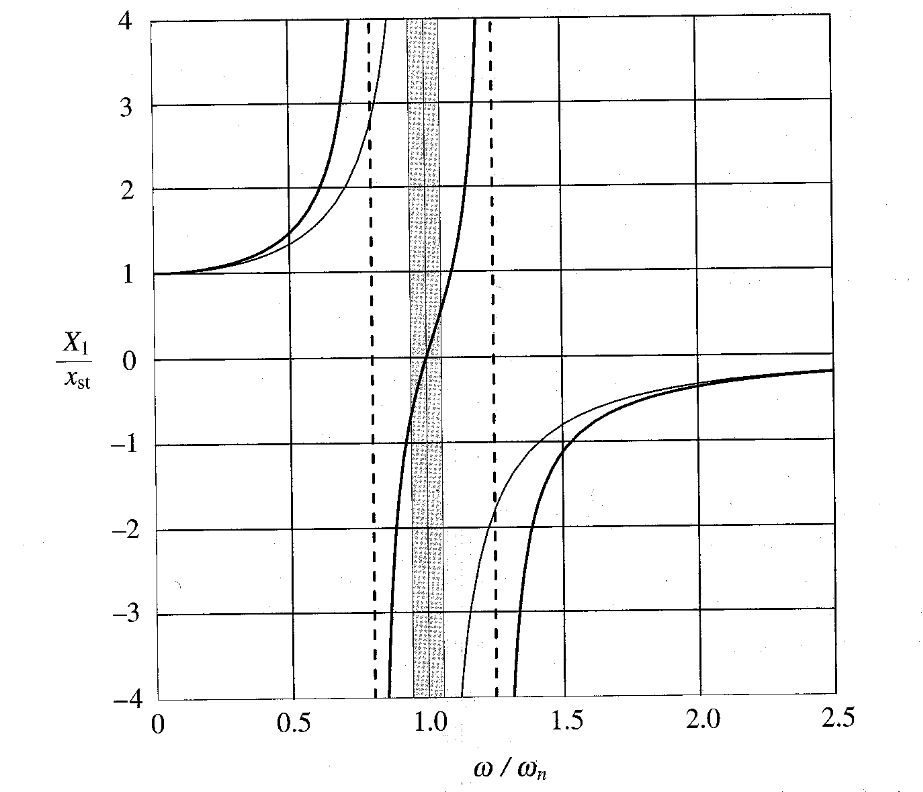
תגובת תדירות למסה הראשית.
הוא תדירות המערכת המקורית (בלי הסופג רטט), ו- הוא - התזוזה/אמפליטודה של המערכת המקורית. (Meirovitch, 2001).
האזור המוצלל בגרף נחשב כהאזור בו תפקוד הסופג רטט נחשב מספיק טוב. נשים לב שאחת מהבעיות בסופג רטט, כפי שמוצג בגרף, הוא שהוא מוסיף עוד תדירות רזוננס.
תרגילים
תרגיל 1
נתונה המערכת הבאה:
סכמת המערכת.
המערכת מורכבת מקפיצי פיתול
הערה:
העובדה שהמערכת סימטרית גאומטרית לא אומר שהיא תהיה סימטרית קינמטית!
נתון:
סעיף א’
נסחו את משוואת התנועה של המערכת.
פתרון:
מספר דרגות החופש בשאלה הוא 5:
ולכן יש 5 דרגות חופש.
מבחינת האנרגיה הקינטית, עבור מסה בודדת יש:
על כל מוט יש שתי מסות ולכן נקבל שסך האנרגיה הקינטית:
או בקיצור:
נגזור לקבלת מטריצת המסה:
מבחינת האנרגיה הפוטנציאלית:
נגזור לקבלת מטריצת הקשיחות:
מבחינת כוחות, במקרה הכללי, פועל מומנט
כך שמשוואת התנועה שלנו היא מהצורה:
נשים לב שמאחר ו-
סעיף ב’
חשבו את קשיחות הקפיצים
פתרון:
על מנת למצוא תדרים עצמיים נפתור בעיית ערכים עצמיים מוכללת של הצמד
ונדרוש פתרון לא טריוויאלי. נדרוש גם, לפי השאלה, שהתדרים העצמיים יהיו מהצורה MATLAB:
סעיף ג’
חשבו את אופני התנודה ותארו אותם גרפית.
פתרון:
על למצוא את המודים נציב את התדירויות במשוואת הערכים העצמיים המוכללת ונפתור מערכת משוואות. נקבל את הוקטורים העצמיים:
הערה:
הסימון (
) מעיד על כך שמדובר בוקטור/גודל ש-לא* מנורמל מסה.
קיבלנו 5 מודים (לכל תדירות עצמית). שלושה סימטריים ושניים אנטי-סימטריים. נוכל לנסח את המטריצה המודלית:
סעיף ד’
חשבו את המודים מנורמלי המסה ומשוואות תנועה בקואורדינטות מודליות.
פתרון:
ניעזר בתכונות האורתוגונליות של המודים:
כאשר
נחשב מסה מודלית לכל מוד (נציב כל פעם מוד אחר). נקבל:
וקטור עצמי (מוד עצמי)
כאשר
מה שאומר ש:
כלומר, כל מוד מחלקים ב-
נשים לב ש:
וגם:
כעת, בעזרת המטריצה המודלית אנו יכולים לבצע מעבר בסיס למשוואות התנועה כדי לקבל משוואות תנועה שהן לא מצומדות. אנו עושים זאת בעזרת קואורדינטות מודליות טבעיות
כלומר, אנו מתארים את הקואורדינטות המוכללות כקומבינציה לינארית של עמודות
נכפיל ב-
נישאר עם:
קיבלנו 5 משוואות לא מצומדות:
להלן אנימציה של 5 המודים. כלומר, בכל גרף מעורר רק אחד מהמודים. בנוסף, כל האנימציות מנורמלות לקצב של תדירות אחידה כדי שהאנימציה תהיה ברורה. במציאות, האנימציה החמישית למשל תהיה פי 5 יותר מהירה מהאנימציה הראשונה.
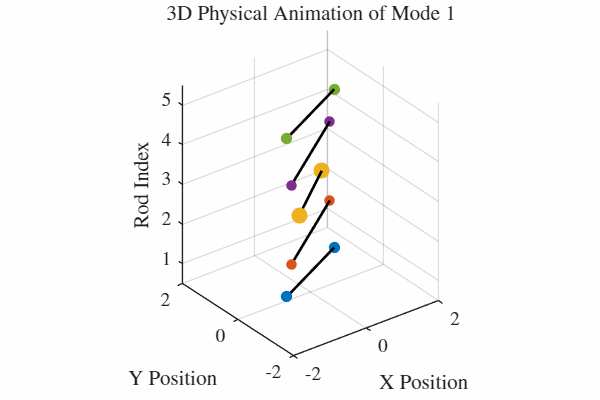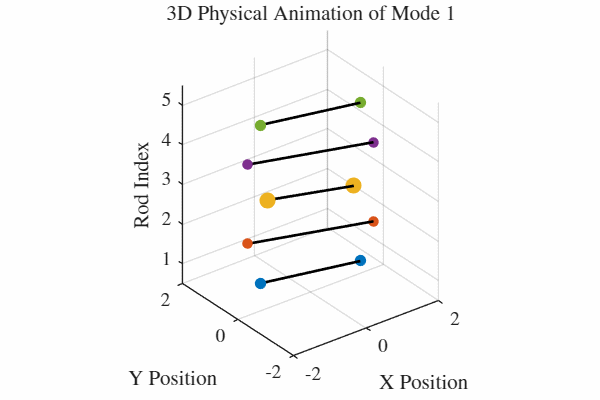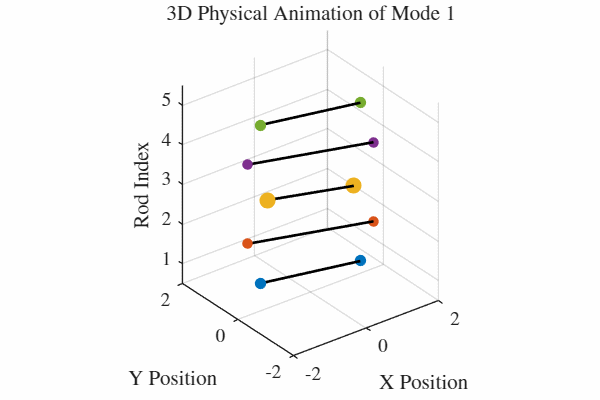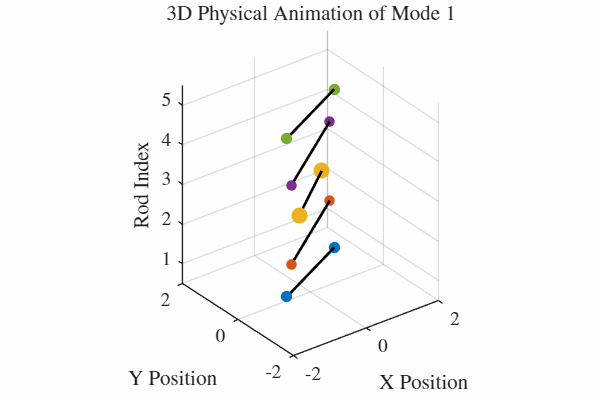
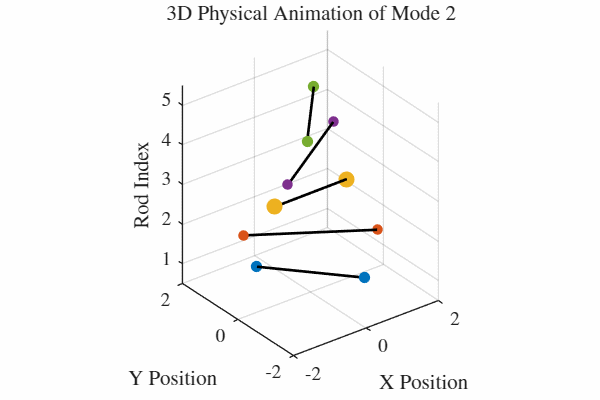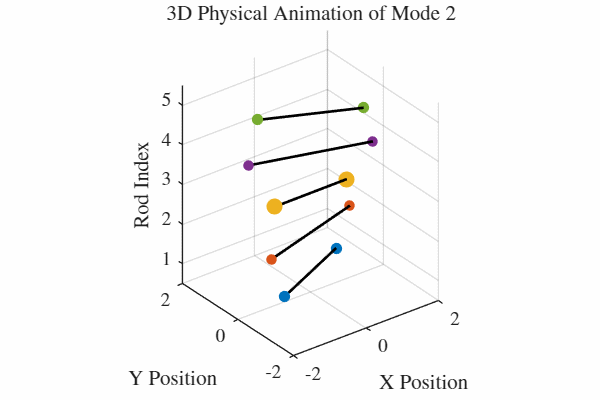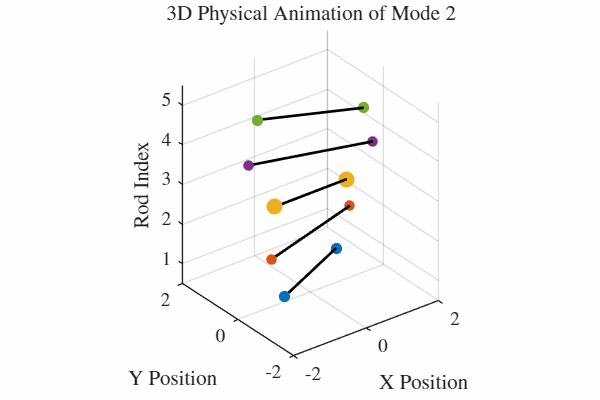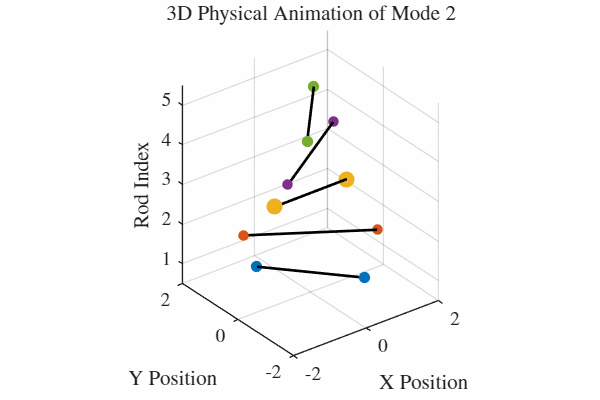
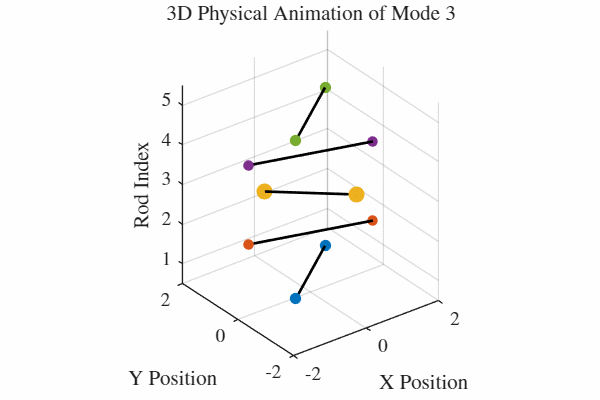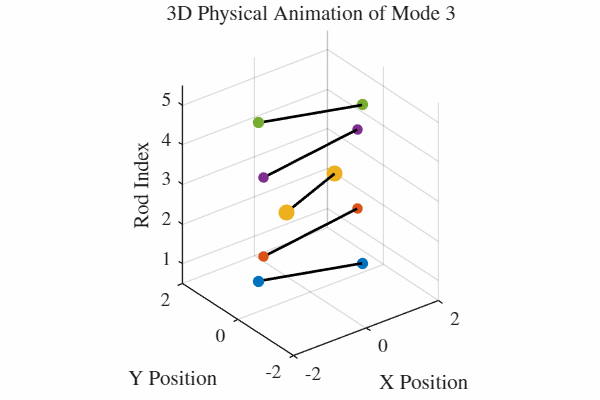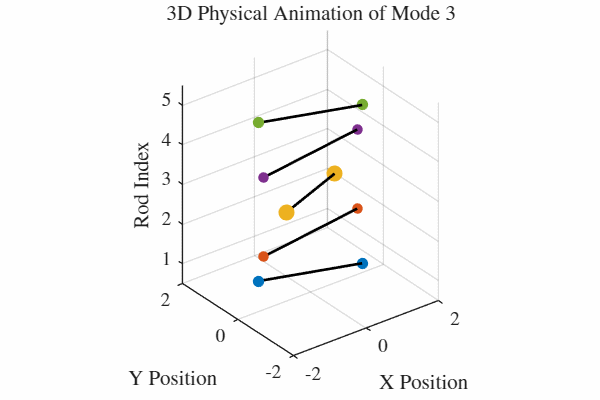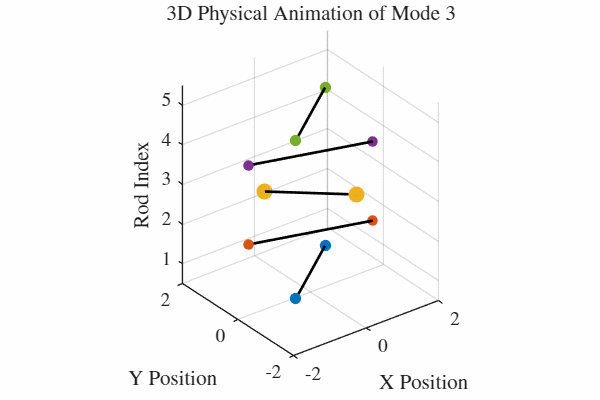
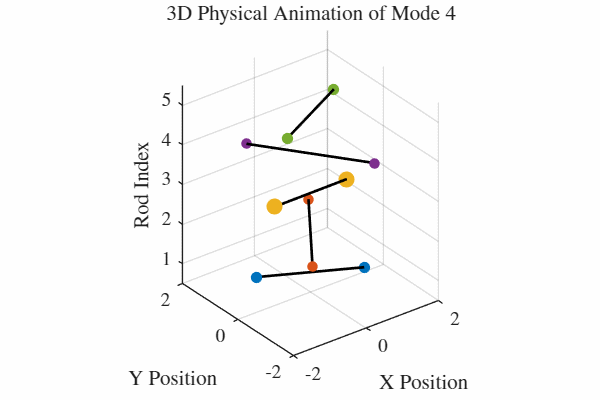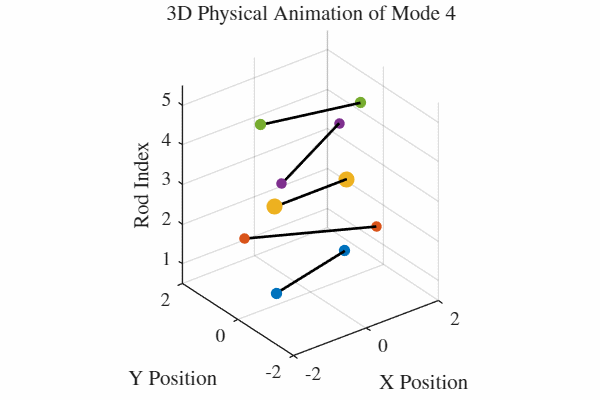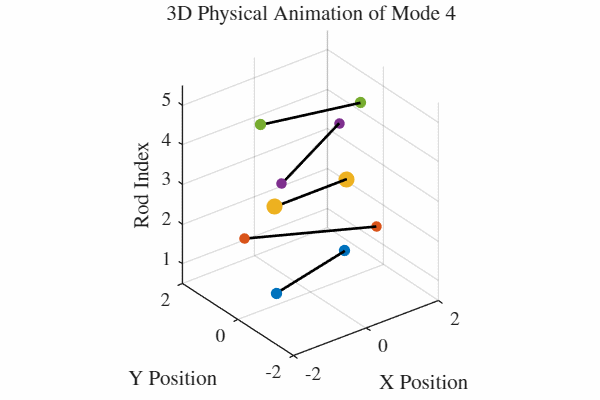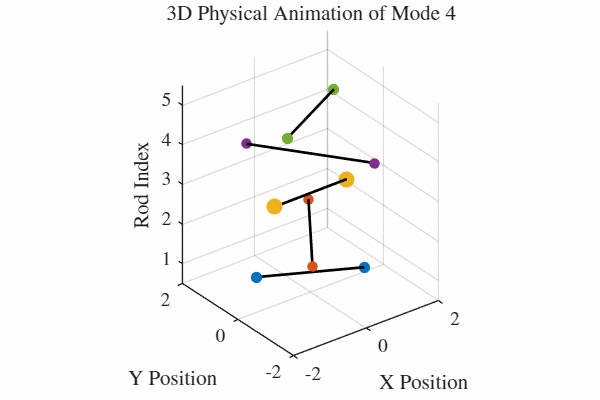
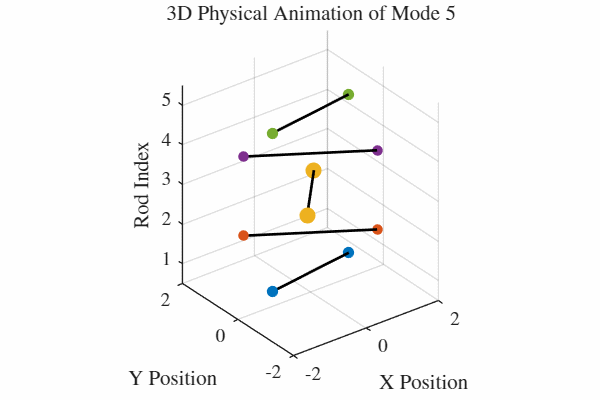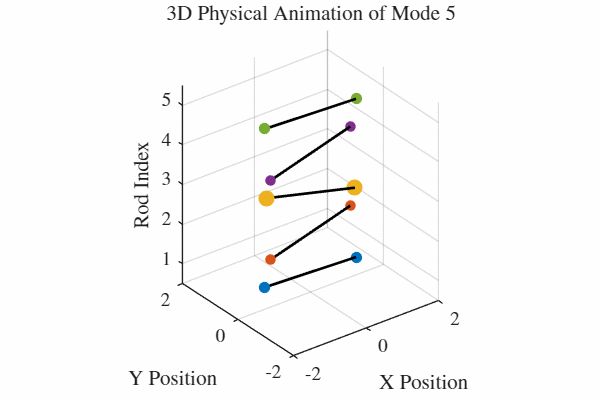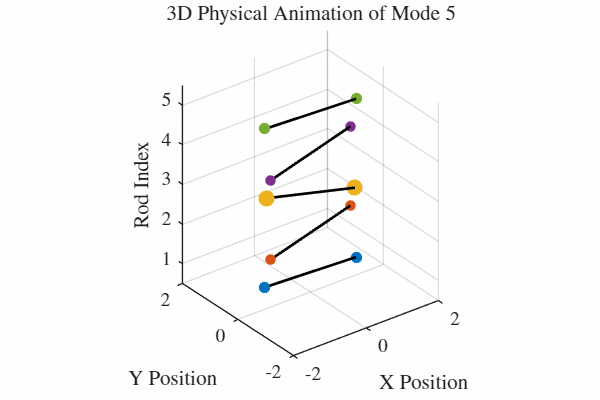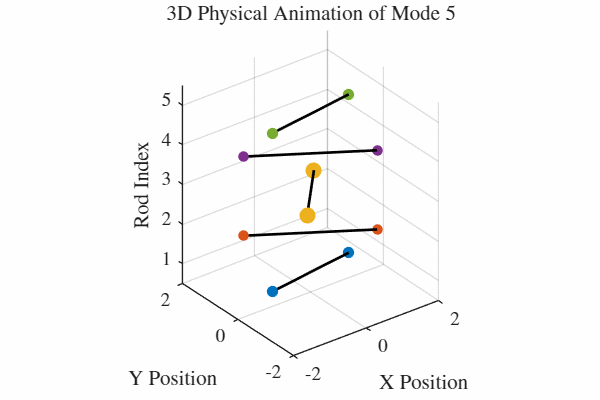
הקוד לאנימציה ב-MATLAB נמצא בGitHub.
תרגיל 2
עם אותה המערכת מתרגיל קודם, ואותם התנודות, ננתח שוב את המערכת רק הפעם עם ריסון
סעיף א’
רשמו את משוואות התנועה של המערכת בקואורדינטות פיזיקליות.
פתרון:
כעת, כיוון שיש ריסון:
בהינתן ריסון מודלי, המערכת הלא מצומדת (בקואורדינטות מודליות) תהיה מהצורה הבאה:
כאשר:
כדי למצוא את
כיוון שאנו לא אוהבים לחשב הופכיות של מטריצה, נוכל במקום זאת להשתמש באורתוגונליות:
מבחינה מספרית, זה יוצא:
נשים לב שאף איבר הוא לא אפס! יש צימוד מלא בין כל דרגות החופש בריסון.
סעיף ב’
חשבו את תגובת המערכת לתנאי ההתחלה:
פתרון:
משוואות התנועה שאנו יודעים לפתור הן:
נמצא את תנאי ההתחלה בקואורדינטות המודליות, בהינתן ת”ה בקואורדינטות פיזיקליות:
נרצה לרשום את מערכת המשוואות במרחב המצב. אם נסמן:
ואז מרחב המצב שלנו הוא:
כאשר זוהי מטריצה שמורכבת מבלוקים - מטריצות אחרות. זו תהיה מטריצה מסדר
נקבל תגובת מערכת עם ריסון - התגובה תדעך:
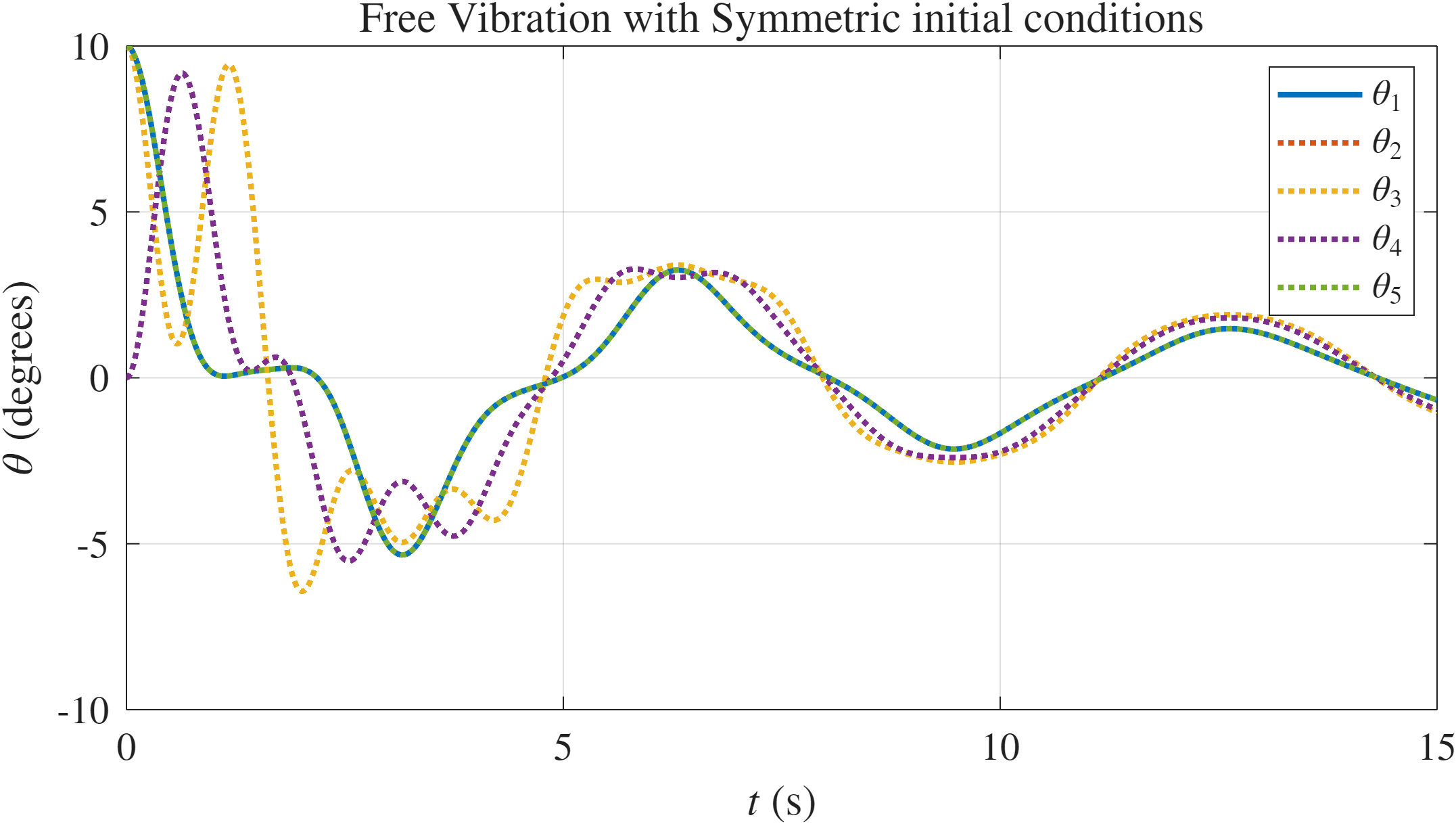
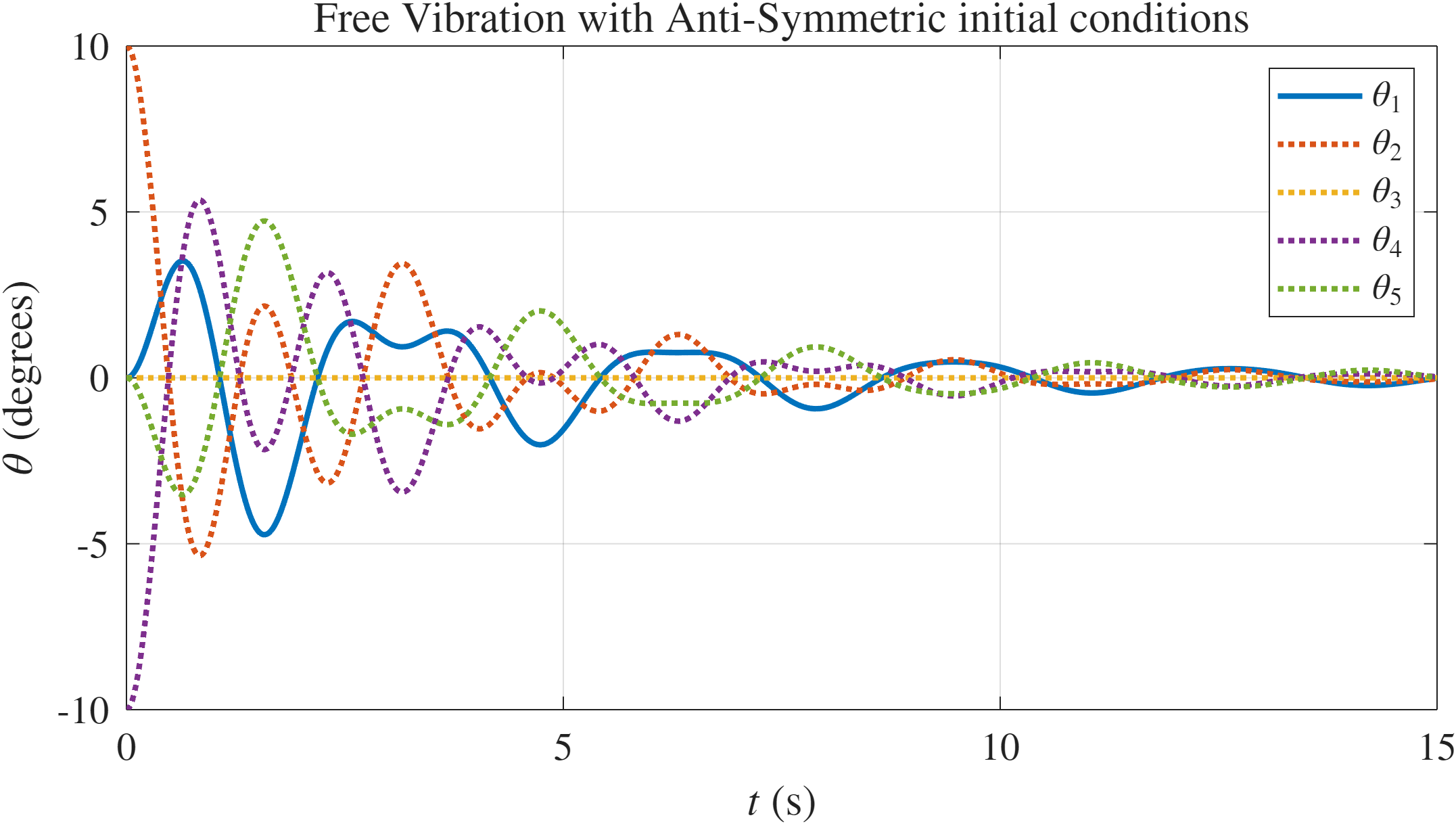
תגובת המערכת לשני תנאי ההתחלה. נשים לב שהמודים המהירים (עם תדר גבוה) דועכים מהר יותר.
הקוד לגרף ב-MATLAB נמצא בGitHub.
סעיף ג’
רשמו ביטוי כללי לתגובת התדירות של המערכת, פעם באמצעות היפוך ישיר ופעם באמצעות סכום מודאלי - סכום תרומות חמשת המודים.
פתרון:
באמצעות היפוך ישיר:
לפי עירורים הרמוניים, או פשוט לפי משפט תגובת התדירות, התגובה של המערכת במצב מתמיד לכוח חיצוני תונד
היא מהצורה:
הערה:
כאן
הוא אמפליטודת המומנט - אין שום קשר למטריצת המסה .
נציב את
נקבל (לאחר חילוק ב-
נעביר אגף:
הביטוי בתוך הסוגריים הוא מטריצת תגובת התדירות
הפונקציה
הבעיה בחישוב מטריצה זו היא שהיא מאוד קרובה לסינגולריות - כמעט בלתי הפיכה. אנו מכירים מנומרית שמאוד קשה לנו לחשב את ההופכי של מטריצות כמעט סינגולריות, בייחוד אם הם מטריצות מסדר גדול. לכן, לרוב נפתור בשיטה הבאה:
פתרון בעזרת סכום מודאלי:
נעבוד באותו האופן רק עם המרחב המודלי:
נציב במשוואות התנועה המודליות ונקבל (לאחר חילוק ב-
נעביר אגף:
שוב יש לנו הפיכת מטריצה, אבל הפעם זו מטריצה אלכסונית לחלוטין! נעבור לקואורדינטות פיזיקליות. כיוון ש-
היפוך של מטריצה אלכסונית הוא פשוט
שימו לב!
נוכל לבצע סכימה מודלית רק עם ריסון מודלי - ריסון שמתלכסן תחת אותו בסיס כמו
ו- !
סעיף ד’
בהנחה ואין ריסון במערכת, אילו מודים משתתפים כאשר המדידה מתבצעת על
פתרון:
נתחיל מ-מדידה על
תגובת התדירות היא:
מאחר ואין ריסון:
נציב מודלים:
נשים לב שתגובה על
כעת, כאשר ה-עירור הוא על
נקבל בסכום המודלי ש-
המודים שמשתתפים הם רק מודים אנטי-סימטריים.
טיפים: המשמעות הפיזיקלית
- אם מתבוננים בדרגת החופש האמצעית לא ניתן לדעת אם מודים
מתעוררים! קוראים לזה non-observable. - אם מפעילים מומנט רק על דרגת חופש אמצעי לא ניתן לעורר את מודים
. קוראים לזה non-controllable.
סעיף ה’
אם העירור פועל על המסה האמצעית, האם קיימים תדרים בהם המסה האמצעית לא תנוע כלל (במצב מתמיד)?
פתרון:
ניעזר בביטוי מסעיף קודם לתגובת המסה האמצעית תחת עירור
נדרוש שביטוי זה,
אם נפתור את המשוואה נקבל 4 פתרונות:
רק
סעיף ו’
שרטטו את תגובת התדירות למסה
פתרון:
נביט בביטוי
נשרטט את הגדלים
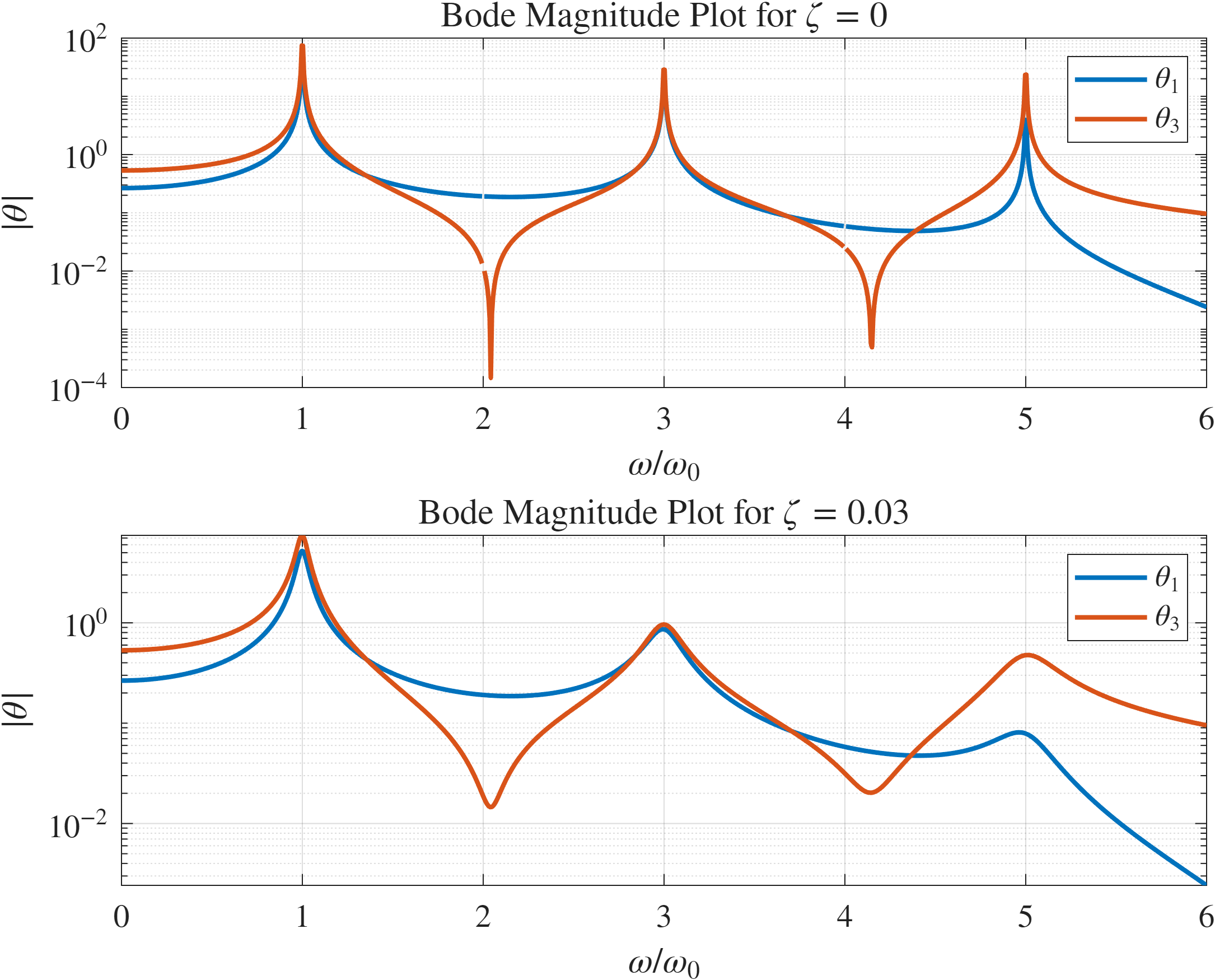
תגובות
ו- בערכי ריסון שונים, במצב מתמיד.
הקוד לגרף ב-MATLAB נמצא בGitHub.
נראה שהביטוי של
