DYN1_HW007 תרגיל בית 7

	סטודנט א’	סטודנט ב’
שם	עידו פנג בנטוב	ניר קרל
ת”ז	CLASSIFIED	CLASSIFIED
דואר אלקטרוני	CLASSIFIED	CLASSIFIED

תרגיל 1

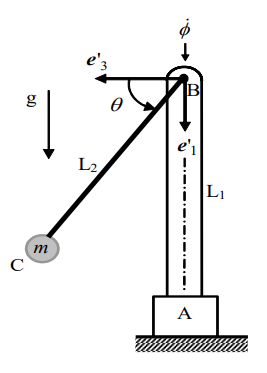
סכימת המוטות

מהגדרת מערכת הצירים:

סעיף א’

וקטור המיקום של המסה:

נגזור פעמיים לפי כלל האופרטור, כאשר נשים לב ש- :

לכן:

סעיף ב’

נמצא את הכוחות שפועלים על :

דג”ח על המסה

לכן השקול כוחות:

לפי מאזן תנע קווי:

סעיף ג’

חתך בקצה המוט

כמו במוצקים 1, נבנה דג”ח על חתך בקצה המוט, ונחשב את כוח הגזירה (הכוח שניצב לכיוון המוט:

נסמן את כיוון ב-, כך ש:

נכפיל את (1) ב-:

מאחר ו- ניצב ל- ו- בכיוון שלו, נקבל:

נציב בחזרה ב-(1) ונקבל:

תרגיל 2

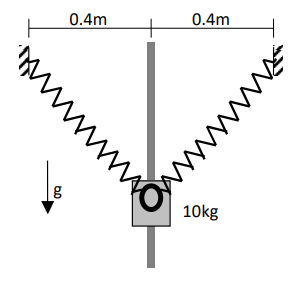
סכימת המסה על המוט

סעיף א’

נשים לב שהכוחות היחידים הפועלים במערכת (פנימיים וחיצוניים) הם כוחות כבידה וכוחות הקפיצים. לפיכך, מתקיים שימור אנרגיה:

בתחילת התהליך, האנרגיה הקינטית:

והאנרגיה הפוטנציאלית:

כאשר הוא האורך ההתחלתי של הקפיצים, ו- הוא האורך הרפוי שלהם.
נציב בשימור אנרגיה:

המרחק המקסימלי אליו תגיע המסה יתקבל כאשר מהירותו מתאפסת (כי ברגע זה מהירותו משנה סימן). נסמן רגע זה ב-, כך שנוכל לומר כי :

כדי לבודד את , נצטרך גם למצוא מהו .

גאומטריית המסה והקפיצים.

ניתן לראות מהגאומטרייה ש- תמיד מקיים:

נציב בשימור אנרגיה:

נציב פרמטרים:

נסמן :

נקבל רק פתרון יחיד פיזיקלי:

סעיף ב’

נסמן את הרגע הדרוש ב-, כך:

שוב, לפי שימור אנרגיה:

נציב פרמטרים:

תרגיל 3

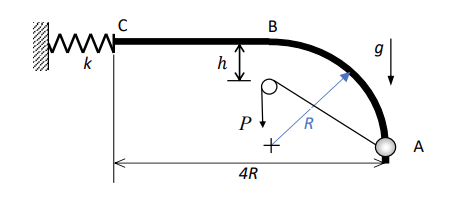
סכימת החרוז

סעיף א’

הכוח מכוון תמיד לנקודה .

נשים לב ש- הוא למעשה כוח מרכזי, שתמיד בכיוון . לפי דוגמה על כוח מרכזי, אנו יודעים שהעבודה שהוא מבצע (השינוי באנרגיה הפוטנציאלית) נתון ע”י:

כאשר הוא שינוי המרחק בין ו-. כלומר:

נשים לב שבהתחלה, מפיתגורס זריז:

נציב נתונים ונקבל:

בסוף, נתון כי . נסיק כי:

כלומר:

סעיף ב’

על החרוז פועלים כוח נורמלי וכוח . הכוח הנורמלי תמיד ניצב למהירות הכדור ולכן הוא לא מבצע עבודה (הוא תמיד ניצב ל-). הכוחות היחידים שנותרו שמבצעים עבודה הם - שהוא כוח מרכזי ולפיכך משמר, וגם כוח הכבידה, שמשמר. קיבלנו שימור אנרגיה:

כאשר הוא מהירות החרוז ב-, ובאותו אופן עבור . נתון כי , ואת מצאנו כבר בסעיף קודם. נציב פרמטרים:

סעיף ג’

דג”ח על החרוז

מעצם הגדרת מקדם החיכוך, מתקיים:

כאשר במקרה הפשוט הנתון, . בנוסף, אנו לא במקרה הסטטי, ולכן נסיק כי בעצם מתקיים שוויון:

כוח זה מופעל לאורך כל המרחק :

ל- ו- כיוונים הפוכים, ולכן:

כאשר המרחק הוא פשוט :

נציב פרמטרים ונקבל:

סעיף ד’

נבצע מאזן האנרגיה הכללי:

הכוח הלא משמר היחיד שביצע עבודה לאורך המסלול מהנקודה ל- הוא כוח החיכוך, ולכן . נפתח גם את שאר ביטויי האנרגיה:

כאשר היא מהירות החרוז בהתכווצות המקסימלית, ו- הם אורכי הקפיץ בזמנים המתאימים ( ברגע שהחרוז היה ב-, ברגע שהחרוז הגיע להתכווצות מקסימלית).
אין הפרשי גובה, ולכן הביטוי המתאים מתאפס. בנוסף, ההתכווצות המקסימלית מתקבלת כאשר מהירות החרוז היא אפס, ולכן .
נניח שבהתחלה אורך הקפיץ הוא אורכו הרפוי, ולכן . נקבל:

נציב ופרמטרים נתונים:

תרגיל 4

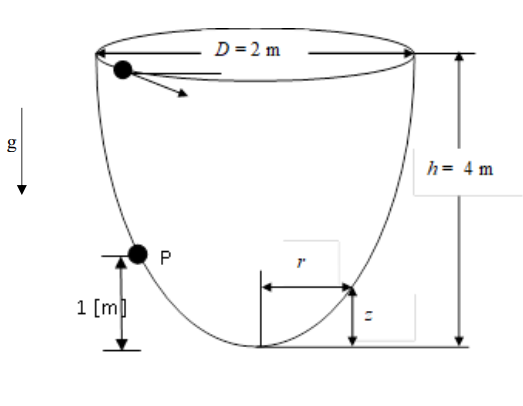
סכימת הקערה

סעיף א’

על החלקיק פועל כוח הכבידה, שהוא כוח משמר, וכוח נורמלי למשטח, שתמיד ניצב למהירותו ולכן לא מבצע עבודה. לפיכך, מתקיים שימור אנרגיה:

נתון ש- וגם . עבור , נתון כי החלקיק נזרק מהחלק העליון של הקערה, ומתיאור פונקציית הקערה וקוטר הקערה ניתן למצוא כי גובה זה הוא:

נציב בשימור אנרגיה ונקבל:

סעיף ב’

נרצה למצוא את וקטור המהירות של החלקיק בנקודה . בקואורדינטות גליליות:

את נוכל פשוט למצוא מהנתון כי גובה הנקודה היא , ופונקציית הקערה היא :

נרצה למצוא את . נבצע זאת ע”י מאזן תנע זוויתי. נשים לב כי הכוחות החיצוניים הפועלים על החלקיק הם כוח נורמלי , שפועל בניצב למישור המשיק לפרבולה, וכוח כבידה .
כיוון הכוח הנורמלי הוא רק ב- ו-, כך שנוכל לרשום . לכן סכום המומנטים סביב , מרכז הקערה:

נשים לב כי המומנט סביב הציר הקבוע מתאפס:

לפיכך, מתקיים שימור תנ”ז סביב בכיוון . כלומר:

נציב את הגדרת התנ”ז:

כלומר, נוכל לומר כי:

בהתחלה, , והמהירות הזוויתית היא . נציב ונקבל:

כדי לקבל את , נוכל לגזור את :

נציב הכל בביטוי ל-:

אנו גם יודעים מהו גודל מסעיף קודם:

כעת אנו יודעים במפורשות את כל אחד מהרכיבים של :

תיאור הוקטור ביחס למישור האופקי

נסיק מהאיור כי:

נציב פרמטרים ונקבל:

סעיף ג’

גודל הכוח שמפעיל החלקיק על הקערה הוא גודל הכוח הנורמלי. כלומר, אנו רוצים למצוא את . נבצע מאזן תנע קווי.

דג”ח על המסה בנקודה

לפי האיור:

נשים לב כי בכלל לא פועל ב-, ולכן נוכל לרשום:

עבור הצד השני של המאזן תנע קווי, עלינו לחשב את התאוצה. בקואורדינטות גליליות:

ממאזן תנע קווי, נקבל שלושה משוואות:

נשים לב ש:

נתמקד רק בכיוונים . נציב פרמטרים:

נסדר כך שנוכל להשוות בין :

נשווה:

נותר לנו למצוא את .

גאומטריית הזווית

מהאיור נסיק כי:

ולכן בנקודה :

נציב בביטוי ל- ונקבל:

סעיף ד’

נרשום מד”ר ע”פ שימור אנרגיה. ראינו בסעיף א’ שמתקיים שימור אנרגיה:

נסמן את צד ימין של המשוואה כהאנרגיה המכנית ההתחלתית:

ולכן:

נציב כללי במערכת קואורדינטות גליליות:

ניזכר כי הוא גודל שמור, כך ש- . לכן:

קיבלנו מד”ר עבור . ניתן לפתור אותה, להציב , וכך למצוא את הזמן.

תרגיל 5

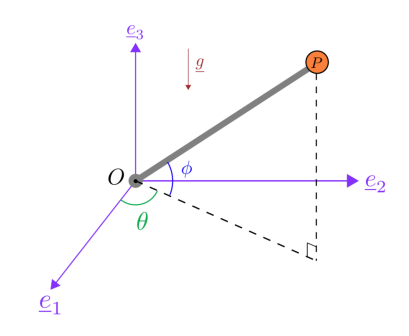
סכימת החלקיק

סעיף א’

מערכת צירים הדרושה היא פשוט מערכת צירים כדורית:

האתגר הוא כעת למצוא את הטרנספורמציה ההפוכה:

סעיף ב’

לפי הגדרת :

ולכן:

כאשר הביטוי בכיוון שלילי כי מוגדר כך ששינוי חיובי ב- הוא סיבוב הפוך בכיוון .
נרשום את הטרנספורמציה ההפוכה, מ- ל-.

מישור והוקטורי יחידה שנמצאים בו

נציב בביטוי ל-:

סעיף ג’

אנחנו נקבל פשוט את הביטויים למהירות ותאוצה בקואורדינטות כדוריות, ללא הביטויים של שינוי אורך . בכל זאת, נבצע לפי כלל האופרטור. וקטור המיקום:

נבנה טבלה:

ולכן:

סעיף ד’

דג”ח על החלקיק והמוט

סעיף ה’

דג”ח על המוט

נסיק כי כיוון הכוח שמפעיל המוט על החלקיק פועל בכיוון המוט - כוח מרכזי בכיוון , כלומר .

סעיף ו’

דג”ח על המסה

נסיק שסך הכוחות הפועלים על החלקיק:

ממאזן תנע קווי:

מפתרון סעיף ג’, קיבלנו שלושה משוואות:

נבודד את הביטויים שאנו מעוניינים בהם:

סעיף ז’

סביב , פועל כוח הכבידה במרחק ממנו:

כלומר:

כדי לבדוק שימור תנע זוויתי, נעבור למערכת צירים קבועה:

כלומר, קיבלנו כי . לפיכך, מתקיים שימור תנע זוויתי בכיוון .

סעיף ח’

נחשב את התנע זוויתי סביב :

מסעיף קודם, אנו יודעים ש- :

כיוון ש- :

אנו יודעים ש- קבוע, ולכן:

סעיף ט’

הכוחות הפועלים במערכת הם כוח הכבידה, וכוח פנימי מרכזי הפועל בין המוט והחלקיק. ניתן גם להחשיב את כוח הריאקציה הפועל . כוח הכבידה והכוח המרכזי הינם כוחות משמרים (כאשר הכוח המרכזי אפילו לא מבצע עבודה), וכוח הריאקציה לא מבצע עבודה כי נקודה קבועה.
לפיכך, מתקיים שימור אנרגיה:

סעיף י’

הכוח המשמר היחיד שמבצע עבודה הוא כוח הכבידה, ולכן:

כאשר הוא גובה המסה בכיוון . מתנאי ההתחלה, נוכל להסיק כי :

בנוסף, :

מבחינת אנרגיה קינטית:

נציב את תנאי ההתחלה במהירות שקיבלנו בסעיף ג’:

ולכן:

נציב בשימור אנרגיה:

אנו יודעים כי . בנוסף, נתון שבהתחלה , ולכן:

נציב:

נוכיח כי :

כיוון ש-, נסיק כי החזקה הרביעית קטנה מהחזקה השנייה, ולכן:

נביט בחזרה בביטוי ל-:

נסיק כי . לפיכך:

נשים לב שב-, מתקיים , אבל נתון כי , כך שהמערכת לא יכולה להגיע למצב בו . המערכת גם לא יכולה לקפוץ בין זוויות שונות - זוהי תכונה רציפה. לכן, נוכל אפילו לומר ש: