DYN1_001 קינמטיקה של חלקיק - מבוא

→ קודם: DYN1_000הבא: DYN1_002 ←

מבוא

סימונים ומוסכמות

נמשיך עם אותם הסימונים ממוצקים 2, כולל ההדלתא של קרונקר ועיקרון הסכימה של איינשטיין.
לעומת זאת, נעבור להדגשת הוקטורים והמטריצות, במקום סימון קו תחתון:

את וקטור המיקום של נקודה ביחס לנקודה סימנו בעבר ב-. כעת, נוריד את הסימן '', ונרשום את האותיות למטה:

טרנספורמציה בין מערכות של וקטורי בסיס

כמו במוצקים 2, נרצה לעבור בין מערכות צירים שונות. אז למשל, עבור שתי מערכות צירים ו-, נוכל לייצג וקטור בעזרת רכיביו בשני המערכות:

כאשר את הרכיבים במערכת נחשב לפי:

את הסקלרים נסמן ב- כך שהקשר בין רכיבי הוקטור בשתי המערכות מוגדר לפי:

תנועה עקמומית במישור

כדי לבנות שפה משותפת לבעיות דינמיקה, אחד מהכלים הבסיסיים שנרצה לפתח הוא תיאור תנועה של חלקיק, שלרוב יהיה לאורך עקומה (במישור או במרחב).

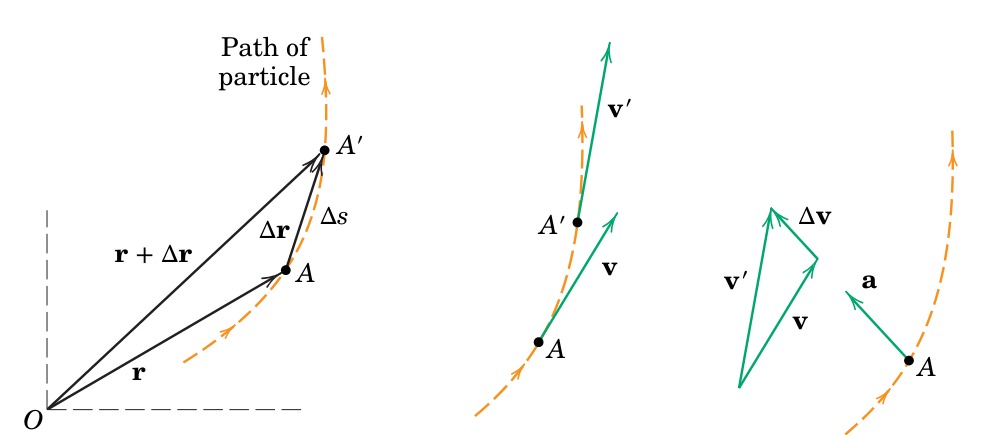
תנועה של חלקיק לאורך עקומה מישורית (Meriam et al., 2018).

בזמן , החלקיק בנקודה , שממוקמת ע”י וקטור המיקום , הנמדד מראשית הצירים . בזמן , החלקיק ב-, הממוקם ע”י .
האורך האמיתי שהחלקיק עבר הוא הסקלר שנמדד לאורך העקומה. לפיכך, נבדיל בין ההעתק למרחק הסקלרי .

בתנועה בליסטית ותנועה מעגלית בפיזיקה ראינו את הנוסחאות המתפתחות עבור חלקיק הנמצא תחת תנאים מסוימים, ועשינו זאת בעזרת הקשרים הדיפרנציאליים:

וגם לפעמים בעזרת שימוש במערכת צירים שונה.

הערה:

הכיוון של שואף לכיוון המשיק לעקומה ככל ש- שואף לאפס. לכן, המהירות תמיד תשיק לעקומה. לגבי התאוצה , נשים לב שהיא לא בהכרח בכיוון המשיק לעקומה, או הנורמלי אליו. אבל, הרכיב הנורמלי שלו תמיד ייפנה למרכז העקמומיות של העקומה.

נביא דוגמאות לשימוש בקואורדינטות שונות.

קואורדינטות נורמליות ומשיקיות

השימוש בקואורדינטות נורמליות ומשיקות לתיאור תנועה של חלקיק היא מאוד נפוצה. קואורדינטות אלו מאפשרות תיאור טבעי לתנועה העקמומית של חלקיק, ולרוב הכי ישירות ופשוטות לשימוש.

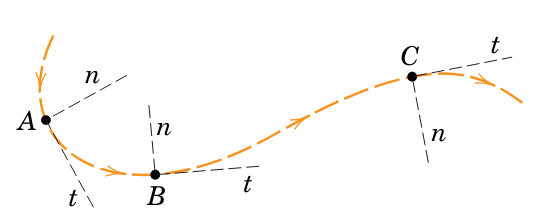
תנועה של חלקיק לאורך עקומה מישורית, והכיוונים של הנורמל והמשיק בנקודות לאורך העקומה. הכיוון החיובי של בכל נקודה תמיד ייבחר לתוך אמצע העקמומיות. לכן, לאורך העקומה הוא עשוי לשנות כיוון (Meriam et al., 2018).

נרצה כעת להשתמש בקואורדינטות ו- כדי לתאר את המהירות והתאוצה . לכן, נסמן וקטורי יחידה בכיוון ו- בכיוון .

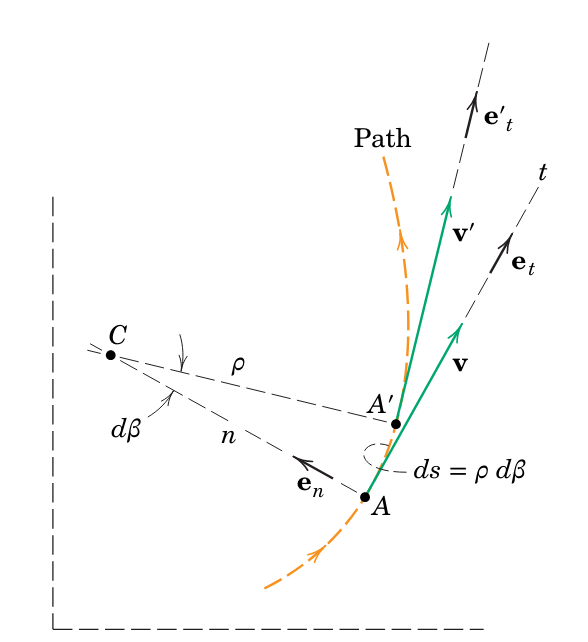
תנועה של חלקיק בפרק זמן (Meriam et al., 2018).

לאחר פרק זמן , החלקיק נע תזוזה לאורך העקומה, מ- ל-. נסמן את רדיוס העקמומיות ב-, ונקבל לפי חישוב אורך קשת במעגל שמתקיים (אין צורך להתייחס לשינוי ב- מ- ל-, ההשפעה שלו זניחה בפרק זמן אינפיניטסימלי ).
לפיכך, גודל המהירות נתון ע”י .
לכן, נוכל לרשום את המהירות של החלקיק באופן הבא:

התאוצה של החלקיק נתונה ע”י:

תאוצה זו מתארת גם השינוי בגודל המהירות וגם השינוי בכיוונו. נגזור את , כאשר נשים לב שגם הגודל שלו וגם הכיוון שלו תלויים ב-, כך שנצטרך לבצע נגזרת של מכפלה:

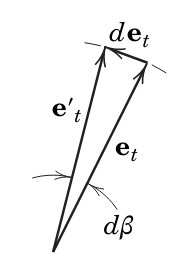
לוקטור היחידה יש נגזרת לא אפסית כי הכיוון שלו משתנה (Meriam et al., 2018).

הוקטור בעל גודל השווה לאורך הקשת - . מאחר ו- הוא וקטור יחידה, נסיק שהגודל של הוא פשוט . הכיוון של הוא פשוט הכיוון הנורמלי, . לכן, אנו יכולים לרשום:

נחלק ב-, ונקבל ביטוי ל-:

הערה:

נשים לב שהנגזרת (לפי זמן) של וקטור יחידה היא לא בהכרח גם וקטור יחידה. הדבר היחיד שאנו יודעים לומר עליה הוא שהיא ניצבת אליו.

נציב בביטוי שקיבלנו עבור התאוצה, כאשר נשים לב ש- :

כאשר:

נוכל לסכם זאת בצורה הבאה:

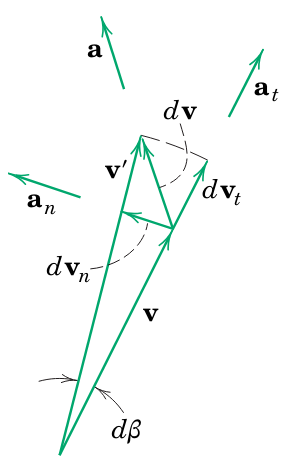
פירוק הוקטורים לרכיב הנורמליים והמשיקים (Meriam et al., 2018).

באיור אנו יכולים לראות את וקטור המהירות כאשר החלקיק נמצא ב-, ו- כאשר הוא נמצא ב-. השינוי בוקטור המהירות הוא , שהוא קובע את כיוון התאוצה .

הערה:

שוב, הרכיב הנורמלי של התאוצה תמיד לכיוון מרכז העקמומיות.

תנועה מעגלית

תנועה מעגלית היא מקרה פרטי של תנועה עקמומית, בו רדיוס העקמומיות קבוע, ונהוג לסמנו ב-. את הזווית נהוג לסמן במקום זאת ב-:

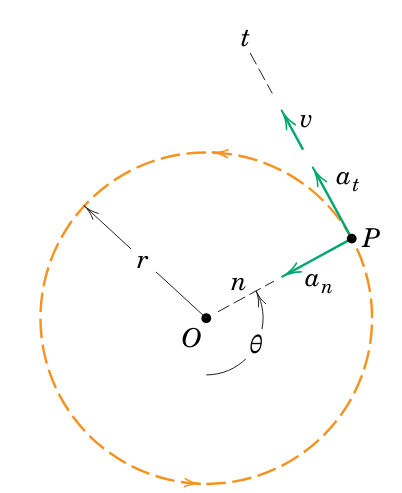
חלקיק הנמצא בתנועה מעגלית (Meriam et al., 2018).

בתנועה זו, גדלי המהירות והתאוצה יהיו נתונים ע”י:

מהירות זוויתית

הביטוי חוזר על עצמו הרבה בפיזיקה, ולכן נהוג לתת לו שם - מהירות זוויתית, כפי שכבר הוגדר בתנועה מעגלית. הכיוון של מהירות זאת מסומן ב- (binormal) והוא מוגדר כהוקטור הניצב גם ל- וגם ל-:

הגדרה:

מהירות זוויתית היא קצב שינוי המיקום הזוויתי של גוף מסוים. היא מסומנת ב- ומוגדרת באופן הבא:

קואורדינטות פולאריות

בקואורדינטות פולאריות החלקיק ממוקם במרחק מנקודה קבועה, ובזווית לקו הרדיאלי.

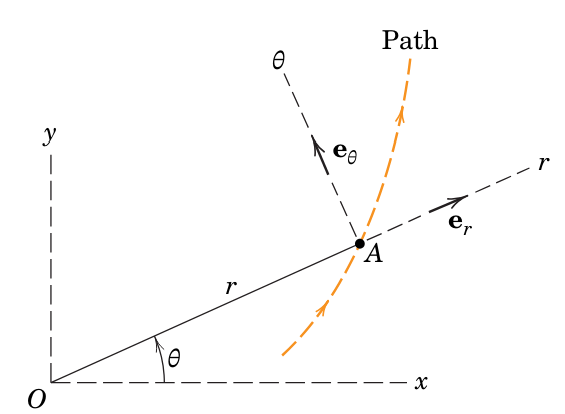
הקואורדינטות ו- הממקמות חלקיק הנע לאורך עקומה (Meriam et al., 2018).

קו שרירותי קבוע, כמו ציר , משומש למדידת הזווית . וקטורי יחידה ו- מוגדרים בכיוונים החיוביים של ו-, בהתאמה. וקטור המיקום אל החלקיק בנקודה בעל גודל השווה למרחק , ובכיוון הנתון ע”י וקטור היחידה . לכן, נוכל לתאר את המיקום של החלקיק ב- ע”י הוקטור:

נרצה לגזור את הביטוי הזה לפי כדי שנוכל לקבל ביטויים עבור ו-. כדי לעשות זאת נצטרך למצוא את הנגזרות ו-. נוכל לעשות זאת כמו שעשינו בפרק הקודם עם .

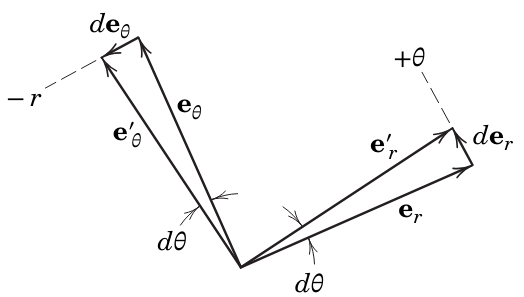
איור עזר לחישוב הנגזרות של וקטורי היחידה ו- (Meriam et al., 2018).

בזמן , כיווני הקואורדינטות מסתובבים בגודל , מ- ו- ל- ו- בהתאמה.
נשים לב שהשינוי בוקטור הוא בכיוון החיובי של ושהשינוי ב- הוא בכיוון השלילי של .
הגודל של השינויים הוא פשוט אורך הקשת (בפרק זמן אינפיניטסימלי), שהוא כי גודל וקטור יחידה הוא . לכן:

נחלק ב-:

או, בצורה השקולה:

כעת נוכל לגזור את לפי :

נציב את שקיבלנו:

כאשר:

הרכיב של מתאר רק את הקצב בו הוקטור נמתח. הרכיב של הוא כתוצאה מהסיבוב של .

נוכל גם לרשום זאת במונחים של מהירות זוויתית:

כדי לקבל את התאוצה, נגזור את לפי , כאשר נשים לב שהנגזרת של תניב שלושה ביטויים, כי כל אחד מהגורמים במכפלה תלוי ב-:

נציב את ו- שקיבלנו:

כאשר:

ניתן גם לרשום את רכיב ה- בצורה:

נוכל לסכם זאת בצורה הבאה:

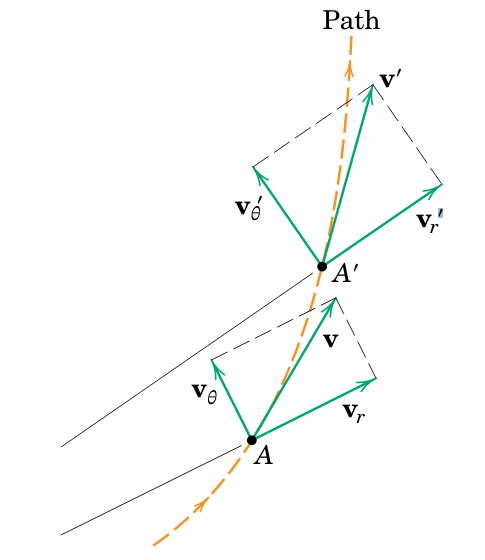
וקטורי המהירות ורכיביהם בנקודה ובנקודה לאחר תזוזה אינפיניטסימלית (Meriam et al., 2018).

כל אחד מרכיבים אלו עובר שינוי בגודל ובכיוון:

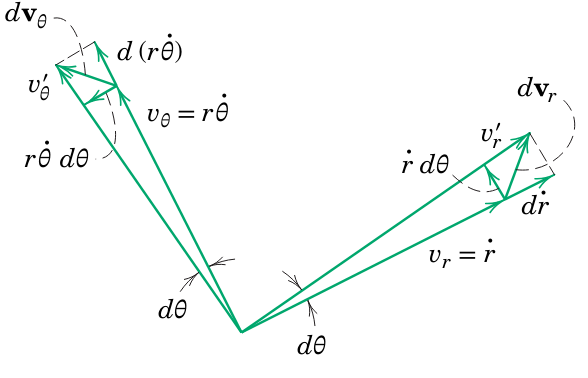
שינויים בגדלים ובכיוונים של רכיבי וקטורי המהירות (Meriam et al., 2018).

• שינוי בגודל של : השינוי הזה הוא פשוט הגדלת האורך של , או . הביטוי לתאוצה המתאים הוא בכיוון החיובי של .
• שינוי בכיוון : מהאיור ניתן לראות שגודל השינוי הוא . התרומה שלו לתאוצה הופכת להיות בכיוון החיובי של .
• שינוי בגודל של : הביטוי הוא השינוי באורך של או , ותרומתו לתאוצה הוא והוא בכיוון החיובי של .
• שינוי בכיוון של : גודל השינוי הוא , ותרומתו לתאוצה היא בכיוון השלילי של .

הערה:

עבור תנועה מעגלית, הוא קבוע. נקבל:

שזה מה שקיבלנו עבור תנועה מעגלית בקואורדינטות ו-, אבל הכיוון החיובי של הוא בכיוון השלילי של . לכן, עבור תנועה מעגלית שמרכזה בראשית הצירים הפולארית.

תנועה עקמומית במרחב

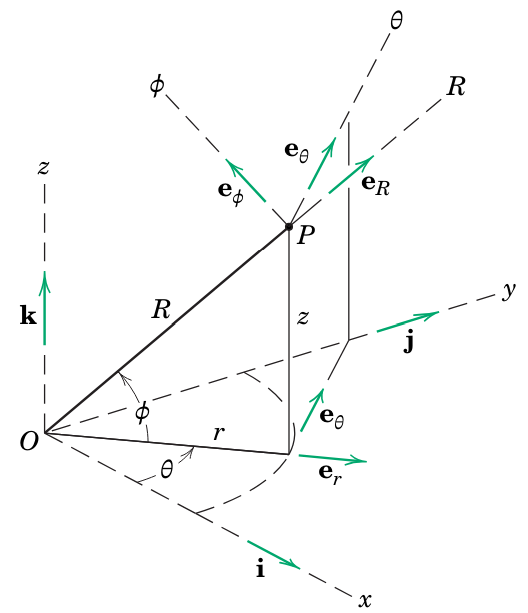
תיאור מיקום של חלקיק בעזרת שלושה סוגים שונים של קואורדינטות (Meriam et al., 2018).

הערה:

בספרות משתמשים בסימונים:

לכן יהיה הבדל בין הסימונים בתרגילים לסימונים בסיכומים.

נעסוק בשלושה סוגים שונים של מערכות צירים במרחב - קרטזית (), גלילית (), וכדורית (), שהם כולם הרחבה של מערכות צירים מישוריות.
השימוש בקואורדינטות הנורמליות משיקיות () במרחב הוא בעייתי - הוקטורים אמנם נמצאים כולם על אותו המישור, אבל מישור זה כל הזמן משתנה.

קואורדינטות קרטזיות

בקואורדינטות קרטזיות, הכיוונים לא תלויים ב-, כך שהנגזרת שלהם אפסית (לא נצטרך לבצע נגזרת של מכפלה). אם וקטור המיקום של החלקיק הוא , אז המהירות והתאוצה נתונים ע”י:

קואורדינטות גליליות

לעומת הקואורדינטות פולאריות, נידרש הפעם להוסיף את הקואורדינטה לוקטור המיקום :

הכיוון לא תלוי בזמן ולכן:

כאשר:

התאוצה תהיה נתונה ע”י:

כאשר:

קואורדינטות כדוריות

בקואורדינטות כדוריות מיקום החלקיק מוגדר ע”י מרחק מראשית הצירים, ושתי זוויות ו- מצירים שרירותיים.

הערה:

כאן מגדירים את כהזווית מהמישור לוקטור הרדיאלי , בשונה מחדו”א 2 בו הגדרנו אותו מהציר לוקטור הרדיאלי (ראו איור בתחילת הנושא).

נגדיר וקטורי יחידה . הביטוי עבור די פשוט לפיתוח, אבל עבור יש כבר טיפה סיבוך, אז לא נראה אותו כאן. נקבל:

כאשר:

וגם:

כאשר:

תנועה יחסית

תנועה יחסית בין שני חלקיקים

לעיתים נוח לתאר מיקום של נקודה במרחב יחסית לנקודה אחרת. וקטור המיקום של נקודה יחסית לנקודה יסומן ב- :

מגזירה בזמן של משוואה זו נובע כי המהירות והתאוצה היחסיות מקיימות את הקשר:

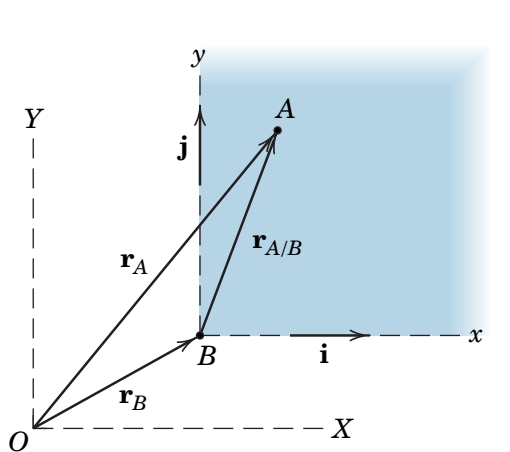
שתי נקודות ו- בעלות תנועות עקמומיות שונות במישור (Meriam et al., 2018).

קצב סיבוב יחסי בין שני חלקיקים

נתונים המיקום והמהירות של שתי נקודות , ודרוש למצוא את קצב הסיבוב של נקודה סביב נקודה . הראנו שקצב השינוי של וקטור נתון לפי:

כאשר הוא קצב הסיבוב של אותו אנו מחפשים. בכדי להיפטר מהאיבר במשוואה, נכפיל את המשוואה ב- ונקבל:

האיבר מתאפס, ומפתיחת המכפלה הוקטורית המשולשת נקבל:

לקצב הסיבוב היחסי לא יכול להיות רכיב בכיוון וקטור המיקום היחסי ולכן:

כדי להבהיר את התוצאה נרשום אותה באופן:

המכפלה מסננת את הרכיב של המקביל ל-, ומחלקת את הרכיב הניצב בגודלו של . מכפלה זו מחולקת בגודלו של . כיוון קצב הסיבוב היחסי נציב למיקום היחסי וניצב למהירות היחסית.

תרגילים

שאלה 1

חרוז נע במהירות קבועה על מוט קבוע במרחב . אל החרוז מחובר מוט קשיח אל חרוז החופשי לנוע על ציר . נתון:
אורך המוט הקשיח .
מיקום החרוז ביחס לנקודה הוא .
מיקום הנקודות ו- .
גודל מהירות החרוז הוא .

תיאור הבעיה הנתונה.

ענו על הסעיפים הבאים עבור :

סעיף א’

מהו ?
פתרון:
מוט קשיח, ולכן המרחק קבוע.

החרוז נע רק על ולכן:

נמצא גם את :

נציב הכל בשתי המשוואות שקיבלנו בהתחלה:

ולכן עבור :

סעיף ב’

מהו ?
פתרון:
נשתמש שוב בנתון שהמרחק בין החרוזים קבוע:

נגזור לפי הזמן:

מסעיף קודם, אנו יודעים ש:

בנוסף, אנו יודעים שהמהירות של היא:

לכן המהירות היחסית (מהירות יחסית ל- ):

אנו יודעים שהוא ניצב לוקטור המיקום, ולכן:

עבור ה- השונים שקיבלנו בסעיף קודם:

סעיף ג’

מהו ?
פתרון:
נתון כי נע במהירות קבועה גם בגודל וגם בכיוון (כי המוט מאלץ אותו) ולכן . לכן התאוצה היחסית הינה:

בסעיף קודם ראינו כי:

נגזור ביטוי זה שוב:

אנו גם יודעים שתנועת החרוז היא רק בכיוון , כך ש- . מכאן נציב את שאר הוקטורים:

נקבל:

נחלץ את :

נציב את זוגות הערכים מסעיפים קודמים:

סעיף ד’

מהו הגודל של התאוצה היחסית ?
פתרון:
התאוצה היחסית הדרושה:

מסעיף קודם, נסיק כי הגודל הוא פשוט:

סעיף ה’

מצאו את היטל המהירות היחסית על וקטור יחידה בכיוון המוט ?
פתרון:
יש למצוא את . נחשב את :

נזכור כי:

מכאן נקבל:

סעיף ו’

חשבו את .
פתרון:
אנו יודעים כי:

ולכן:

כמו כן:

ולכן:

כך שהמכפלה הוקטורית היא פשוט:

מכאן נקבל עבור שקיבלנו:

סעיף ז’

חשבו את הנגזרת בזמן של .
פתרון:
נוכל פשוט לגזור לפי כללי נגזרת של מכפלה:

כאשר:

נוכל כעת לחשב את המכפלה הוקטורית:

מכאן נקבל עבור שקיבלנו:

סעיף ח’

חשבו את .
פתרון:
נשתמש בזהות של מכפלה וקטורית משולשת (bac to cab):

נציב נתונים מסעיפים קודמים:

נציב בחזרה במכפלה המשולשת:

נציב את שני ה--ים השונים שלנו:

שאלה 2

חרוז ממקום בתוך צינור חלול . החרוז מחובר באמצעות חוט באורך לנקודה קבועה במישור. ברגע מתלכד כיוון המוט עם כיוון . המוט שאורכו והינו סובב במהירות זוויתית קבועה סביב ציר ה-.

תיאור הבעיה הנתונה.

באמצעות הנתונים והקואורדינטה חשבו:

סעיף א’

מהם וקטורי המהירות המוחלטת והתאוצה המוחלטת של החרוז ברכיבי המערכת הקוטבית?
פתרון:
נוכל לרשום את וקטור המיקום של החרוז בצורה הבאה (במערכת גלילית):

גאומטריית המצב.

מגאומטרייה, מאחר והמשולש שווה שוקיים והנתונים:

מטריגונומטריה:

נציב כדי לקבל:

נגזור:

נשים לב כי וגם .
כדי לקבל את המהירות, נגזור כאשר נשים לב שאנו בקואורדינטות גליליות:

באותו אופן עבור התאוצה:

סעיף ב’

מהו וקטור המהירות של החרוז ברכיבי המערכת הקבועה?
פתרון:
נוכל לבנות את הקשר בין המערכת צירים הקרטזית לגלילית:

כעת נציב בתוצאות מהסעיף הקודם:

לאחר פישוט של הפתרון ע”י זהויות טריגונומטריות, נקבל:

סעיף ג’

מהו וקטור התאוצה של החרוז ברכיבי המערכת הקבועה?
פתרון:
כמו בסעיף קודם, נציב את הקשרים בין מערכות הצירים בתוצאות שלנו מסעיף א’. נקבל:

סעיף ד’

מהו וקטור הכיוון של המהירות המוחלטת ברכיבי המערכת הקוטבית?
פתרון:
וקטור הכיוון של המהירות המוחלטת של החרוז, במערכת הצירים הגלילית:

שאלה 3

המוט מוחזק בזווית קבועה וסובב סביב ציר אנכי העובר דרך נקודת הקצה במהירות זוויתי קבועה ונתונה . החלקיק מחליק לאורך המוט בתנועה מחזורית ביחס למוט, כאשר מרחקו מנקודה הוא .

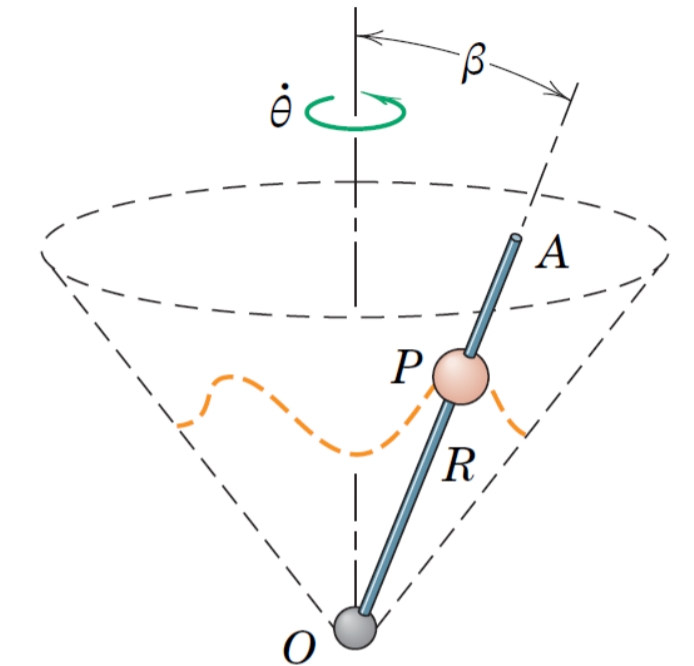
תיאור הבעיה הנתונה.

סעיף א’

בטאו את רכיבי המהירות המוחלטת והתאוצה המוחלטת של החלקיק כתלות בקואורדינטות ונגזרותיהן:

1. במערכת צירים כדורית.
2. במערכת צירים גלילית.
3. וודאו את התוצאות באמצעות מציאת גודל המיקום, גודל המהירות, וגודל התאוצה בשתי מערכת הצירים.

פתרון:
נשים לב שהקואורדינטות במערכת זו, ביחס למערכת כדורית הן:

לכן הנגזרות:

במערכת כדורית אנו יודעים כי מיקום החלקיק נתון ע”י:

לפי נוסחאות למהירות ותאוצה במערכת כדורית:

באותו אופן עבור התאוצה:

במערכת צירים גלילית, ביחס למערכת הצירים הכדורית:

נציב את כדי לקבל:

נציב במיקום מסעיף קודם כדי לקבל:

נשים לב כי:

נגזור:

נזכור כי ו- . לפי קואורדינטות גליליות:

נוודא שוויון בין שתי התוצאות שלנו ע”י השוואה של הגדלים .
במערכת כדורית:

באותו אופן עבור המערכת הגלילית, נקבל שהגלים שווים.

סעיף ב’

יש לחשב את גודל תאוצת החלקיק במצב בו מהירותו ביחס למוט היא מירבית. השתמשו בנתונים הבאים:

פתרון:
נגזור את הביטוי של פעמיים:

נקבל כי מקסימלי כאשר , כלומר:

במקרה זה וגם .
נציב את הערכים שקיבלנו:

ולכן:

→ קודם: DYN1_000הבא: DYN1_002 ←