FEM1_E2020SA 2020 אביב מועד א

שאלה 1

נתון:

סעיף א’

נבצע אינטגרציה:

נכפיל בפונקציית בוחן ממרחב הפונקציות הקבילות קינמטית:

נבצע אינטגרציה בחלקים על הביטוי השלישי בצד שמאל ונישאר עם:

נשים לב שיש לנו תנאי שפה דיריכלה בצד שמאל וימין. לפיכך, .

סעיף ב’

נבצע את הקירובים:

לפיכך, נוכל לרשום:

כאשר:

עבור שלושה אלמנטים לינאריים באורך שווה, כל אלמנט הוא באורך . נבחר את פונקציות הבסיס באלמנט המאסטר כ:

כך שהמיפוי הוא:

נסמן ונשים לב ש:

לפי פיתוחים שנראו בהרצאה, בעזרת אינטגרציית גאוס בנקודה אחת נוכל לרשום:

ולכן המטריצה הגלובלית:

באותו אופן עבור שאר המטריצות:

ולכן הגלובלית:

כך ש:

וגם:

מאחר ויש לנו תנאי שפה דיריכלה הומוגניים, המערכת המשוואות שלנו מצטמצמת לשתי משוואות (שורה שתיים ושלוש):

סעיף ג’

נתון:

נמצא את . לאחר הצבת תנאי השפה, היא מטריצה הפיכה, כך שנוכל לרשום:

לכן נוכל לרשום:

נציב ב-(E1.1) ו-(E1.2):

סעיף ד’

נשים לב שאנו כבר יודעים מתנאי ההתחלה ש:

כלומר:

כעת לפי (E1.3):

לפיכך:

נזכור כי הקרוב שלנו היה . לפיכך:

אין לי כוח לחשב את .

סעיף ה’

לא אם רוצים להבטיח יציבות בזמן.

סעיף ו’

כן כי שיטות סתומות יציבות בזמן ללא תנאי.

שאלה 2

נתון:

כאשר הוא טנזור אלכסוני המייצג את מוליכות החום.

הערה:

אני משתמש כאן בסימונים אחרים כי הסימונים שהם נותנים תמיד מבלבלים רצח ולא עקביים בכלל עם הסימונים שאנחנו מכירים ממעבר חום.

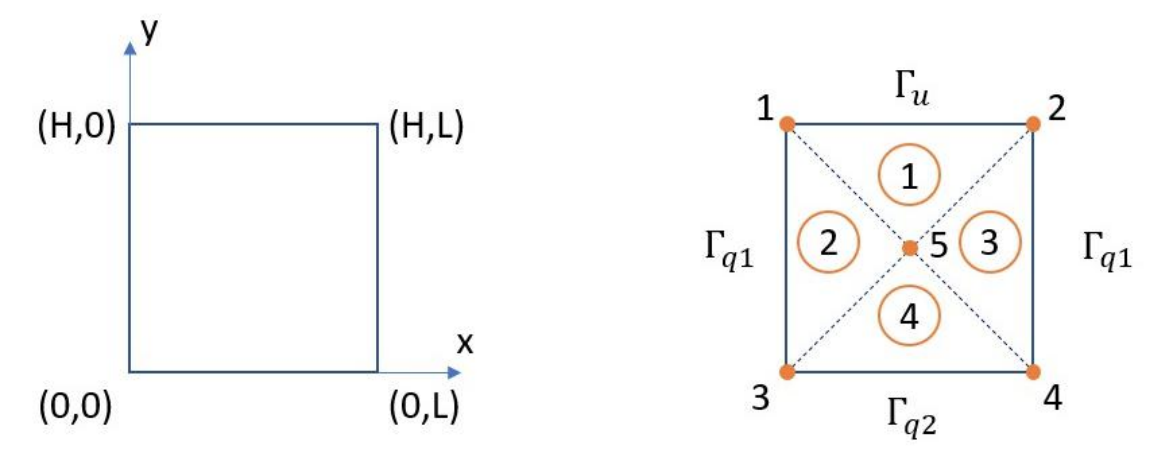
איור E2020.1: סכמת הבעיה ותחום הרישות.

סעיף א’

נבצע אינטגרציה על התחום:

נכפיל בפונקציית בוחן קבילה קינמטית:

נשתמש בזהות . או לאחר העברת אגפים:

נבחר ו-. נציב במאזן לעיל:

בעזרת משפט הדיברגנץ על הביטוי הראשון באגף שמאל:

מאחר ו- קבילה קינמטית, היא מתאפסת בקצוות בהם יש תנאי שפה דיריכלה . בנוסף, מתאפס בקצוות בהן יש תנאי שפה נוימן הומוגני . לפיכך, נישאר רק עם :

אנחנו יודעים שעל שפה זו:

ולכן:

לאחר טיפה העברת אגפים:

סעיף ב’

לפי השרטוט:

מיקום כל הצמתים:

תנאי שפה דיריכלה:

תנאי שפה נוימן:

סעיף ג’

דרגות החופש שאלמנט זה משפיע עליהן הן .
עבור המקרה של אלמנט משולש, אנו בוחרים את פונקציות הבסיס:

ואז מטריצת הקשיחות האלמנטרית היא:

כאשר:

כדי לחשב את נשים לב ש:

כך ש:

לכן:

נוכל כבר לחשב את:

נציב ב-(E2.1) ונבחר נקודת אינטגרציה אחת כך ש:

נקבל:

נחשב כעת את וקטור העומס. נתחיל ממטריצת המסה:

ולכן:

כאשר הם ערכי בצמתים המתאימים. לסיכום:

סעיף ד’

לפי הטבלה מסעיף ב’:

שאלה 3

סעיף א’

פשוט חישוב גודל רשת אופטימלי.

סעיף ב’

מתואר באינטגרציית גאוס.

סעיף ג’

בשלב הזה אני כבר מעתיק את הפתרון הרשמי כי למה לא:

עבור אלמנטים חד-ממדיים, תמיד יש צומת משותף אחד בין האלמנטים, ללא תלות בסדר האלמנט. רוחב פס המטריצה הינו הצר ביותר האפשרי (מטריצה תלת-אלכסונית עבור אלמנט ליניארי, מטריצה -אלכסונית עבור קוודרטי, וכן הלאה). עבור אלמנטים דו-ממדיים מרובעים, קיימות שתי אפשרויות: אם האלמנטים חולקים פינה ואינם חולקים צלע – במקרה כזה יהיה צומת משותף אחד ללא תלות בסדר האלמנט. אם האלמנטים חולקים צלע, אז עבור מרובע בי-ליניארי ( צמתים) נקבל צמתים משותפים, ועבור מרובע בי-קוודרטי או מרובע “סרנדיפיטי” נקבל צמתים משותפים. מבחינת רוחב הפס, לא ניתן להגיד ד בר בצורה חד משמעית, מפני שהדבר תלוי חזק במספור הגלובלי של הצמתים.

סעיף ד’

פתרון רשמי:

טטרהדר הינו פירמידה בעלת בסיסים משולשים, כלומר פאות, צלעות, ו- קודקודים. בטטרהדר ליניארי יהיה צומת בכל קודקוד, צמתים בסה”כ. עבור בעיה סקלרית (דרגת חופש אחת בכל צומת( האלמנט יקבל מטריצה ועבור בעיה וקוטרית ( דרגות חופש בכל צומת(. בטטרהדר קוודרטי יהיה צומת בכל אחד מהקודקודים, וצומת במרכז כל אחת מהצלעות, צמתים בסה”כ. לכן עבור בעיה סקלרית תתקבל מטריצה ועבור בעיה וקוטרית .