| קורס | אלמנטים סופיים לאנליזה הנדסית |
|---|---|
| מספר קורס | 00350022 |
| סטודנט א’ | |
|---|---|
| שם | עידו פנג בנטוב |
| ת”ז | CLASSIFIED |
| דואר אלקטרוני | CLASSIFIED |
שאלה 1
נביט בפונקציה:
סעיף א’
אנו יודעים שסביב
לכן נוכל לרשום:
אם ניקח רק את שלושת הביטויים הראשונים:
סעיף ב’
נדרש למצוא קירוב אינטרפולציה של
כאשר
כדי להגיע לשגיאת חיתוך מסדר
באופן כללי, עבור אינטרפולציית לגראנז’ עם
לכן, האורך של הווקטורים
פולינומי לגראנז’
כאשר
אם נפתח כל אחד מהפולינומים, נקבל:
לפי הגדרת הקרוב,
סעיף ג’
כתבנו קוד MATLAB שמחשב את האינטרפולציה ומשווה אותה לפונקציה המקורית. הקוד נמצא ב-GitHub.
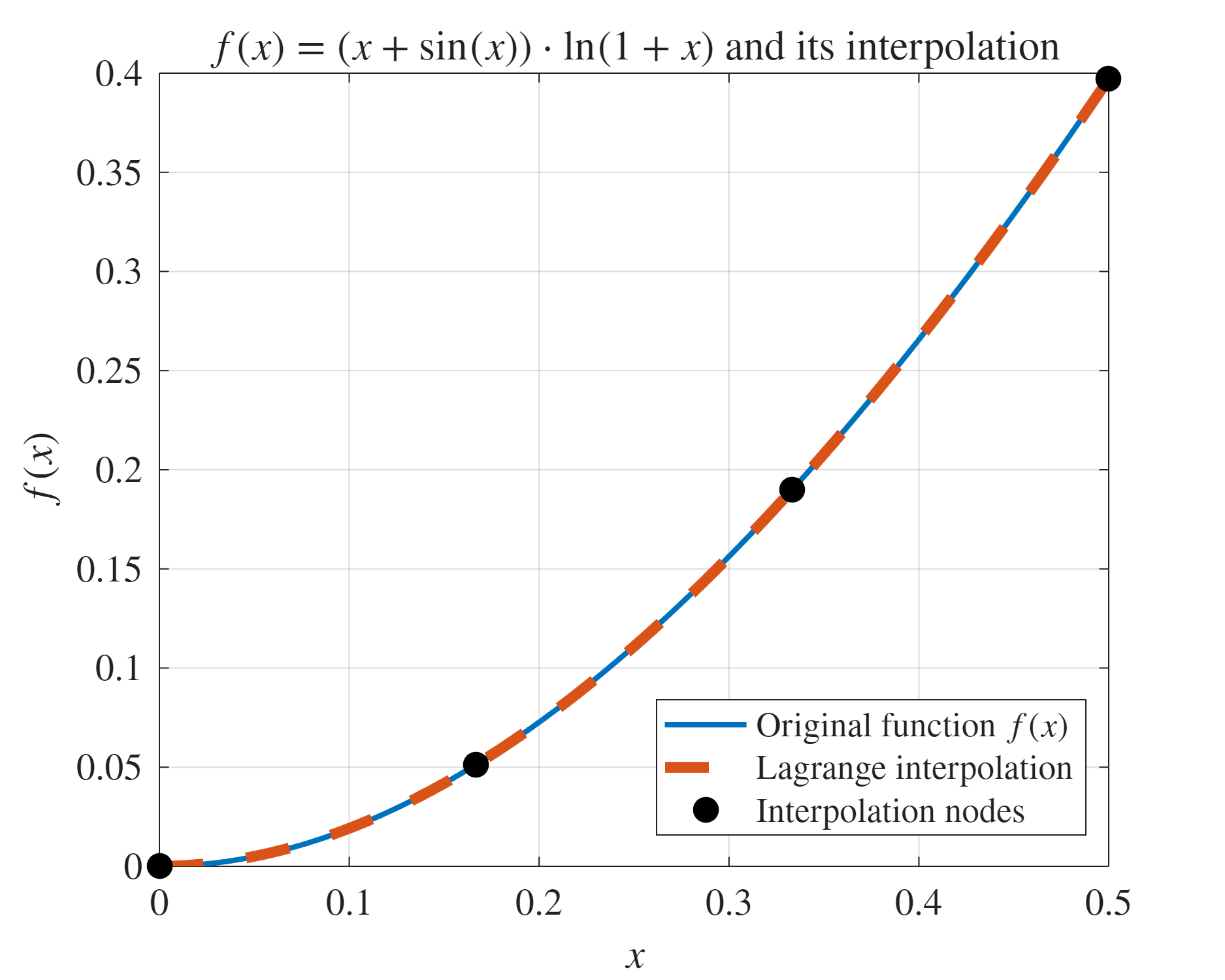
השוואת הפונקציה המקורית והקרוב שלה.
הקוד מחשב את ערכי הפונקציה בנקודות האינטרפולציה, ואז משתמש בפולינומי לגראנז’ כדי לחשב את הקירוב בכל נקודה ב-
התוצאות מראות שאינטרפולציה עם
Maximum interpolation error: 1.80e-04
Expected error order: O(h^4) = 7.72e-04
שאלה 2
הפונקציה המשלימה לפונקציית השגיאה מוגדרת באופן הבא:
נדרש לכתוב פונקציה שמקבלת
התמרת האינטגרל מקטע אינסופי לקטע סופי:
האינטגרל שאנו מחשבים הוא מ-
כדי לחשב אותו עם שיטת גאוס-לז’נדר, צריך להמיר אותו לאינטגרל על קטע סופי. נשתמש בהחלפת המשתנים:
שממפה את התחום
ולכן האינטגרל הופך להיות:
שיטת אינטגרציית גאוס:
באינטגרציית גאוס, האינטגרל מקורב כסכום משוקלל של ערכי הפונקציה בנקודות מסוימות:
עבור
- נקודה:
- משקל:
עבור
- נקודות:
- משקלים:
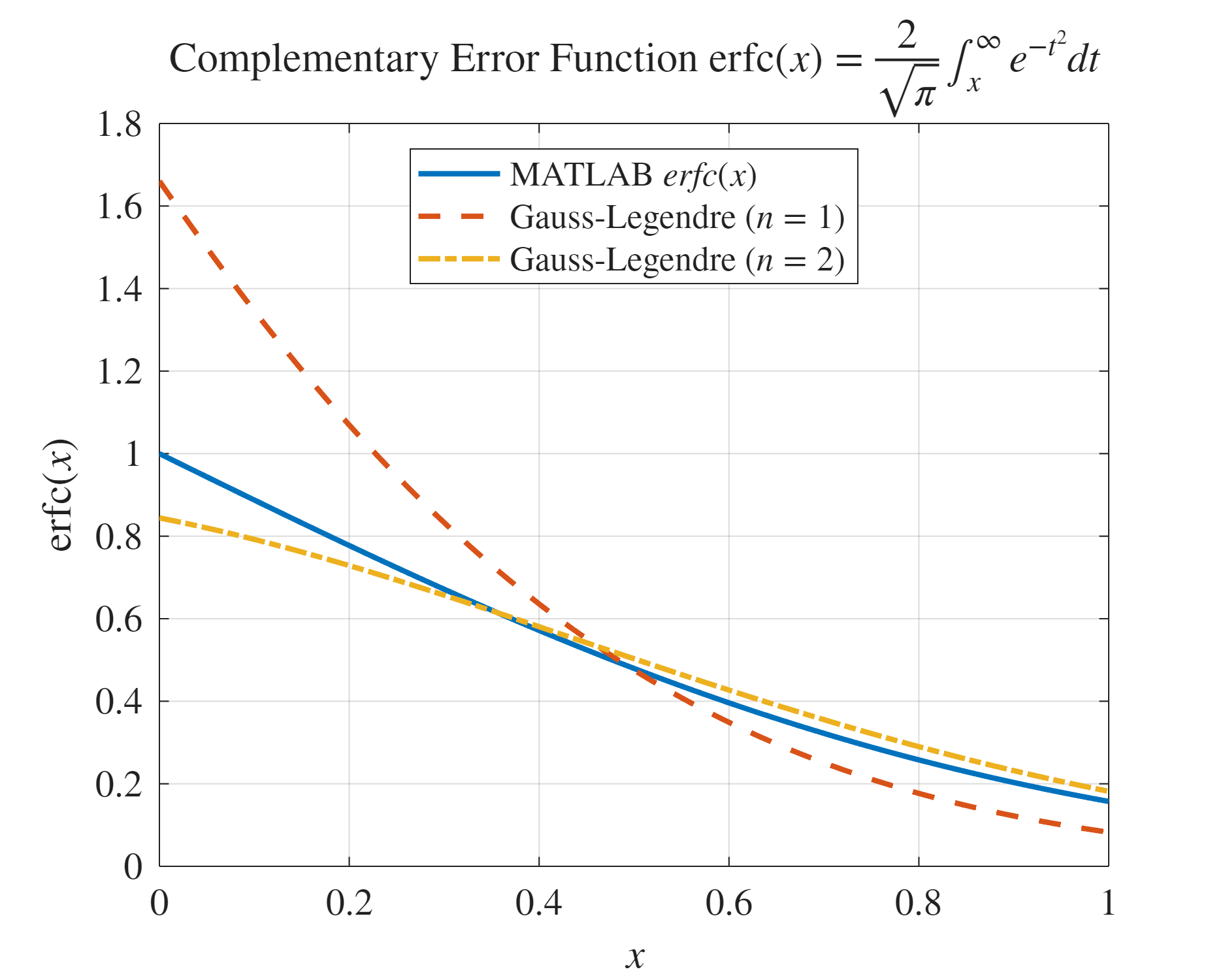
פונקציית השגיאה לעומת קרובים שלה לפי אינטגרציית גאוס.
קוד לחישוב פונקציית השגיאה המשלימה נמצא ב-GitHub.
