NUM1_007 אינטרפולציה פולינומית

→ קודם: NUM1_006הבא: NUM1_008 ←

מבוא

אינטרפולציה היא מקרה פרטי של קירוב. היא יודעת לתת לנו ערך שלא מדדנו (למשל מניסוי), בהינתן מדידות קרובות מספיק (כמו בבטבלאות קיטור. סוג אחר של אינטרפולציה יודעת לבצע קירובים של פונקציות מסובכות, כמו למשל טיילור.

אינטרפולציה פולינומית היא בסיס לאלגוריתמים יותר מסובכים בגזירה, אינטגרציה, פתרון משוואות דיפרנציאליות ותחומים אחרים. לכן, אינטרפולציה פולינומית היא פעולה חשובה שחוזרת שמופיעה המון.

קירוב כללי ואינטרפולציה

ניתן להבדיל שיטות קירוב לשני סוגי בעיות:

1. התאמת נתונים:
   בהינתן קבועה של נקודות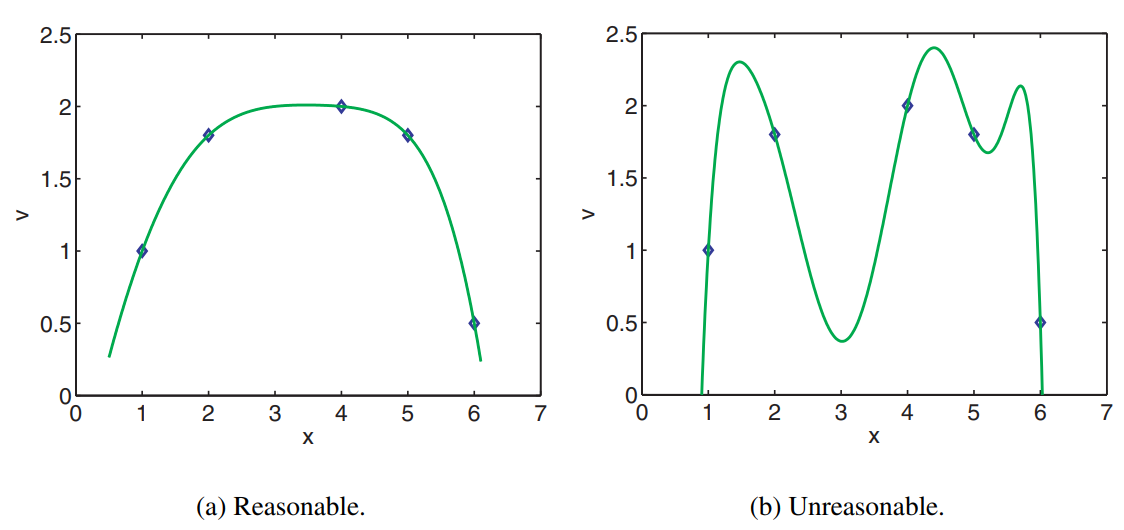 , מצאו פונקציה סבירה שמתאימה לנקודות אילו. אם הנקודות הנתונות הן נקודות מדויקות (ולא קירובים כלשהם), נדרוש ש- תהיה אינטרפולציה של הנתונים. כלומר, שהפונקציה תעבור בדיוק בנקודות:
2. קירובי פונקציות:
   עבור פונקציה מסובכת , מצאו פונקציה שמהווה קירוב ל-. למשל, אם נצטרך למצוא מהר קירוב טוב של הערך , רק עם מחשבון פרימיטיבי, האם יש פונקציה אחרת שנותנת ערך מספיק קרוב ל-?

אינטרפולנט והצגתו

לרוב, נניח צורה לינארית לכל הפונקציות אינטרפולציה . כלומר:

ל- אנו קוראים אינטרפולנט, הם מקדמים לא ידועים שנוכל לחשב מנתונים, ול- נקרא פונקציות בסיס.

בנוסף, אנו נניח כי פונקציית בסיס הן בלתי תלויות לינארית. לפיכך, אם , אז בהכרח לכל .
נשים לב כי אנו מניחים גם שמספר הפונקציות בסיס שווה למספר הנקודות הנתונות, . אם ישנם פחות פונקציות בסיס מנקודות נתונות, אנו נבצע את שיטת הריבועים הפחותים שנלמד בהמשך.

ככלל, נוכל לרשום את התנאים על האינטרפולציה בצורת מערכת משוואות לינארית:

הנה מספר סוגים שונים של אינטרפולנטים:

• אנו נעסוק באינטרפולציה פולינומית: כלומר, פונקציות הבסיס שלנו הן:
• עוד סוג הוא אינטרפולציה טריגונומטרית:

אינטרפולציה פולינומית

נסמן את האינטרפולנט הפולינומי עד סדר ב-:

עבור נקודות מידע:

אנו רוצים למצוא מקדמים כך ש:

בנוסף, נניח ש:

דוגמה:

יהי , והנקודות:

אנו רוצים למצוא פולינום מסדר לכל היותר מהצורה:

העובר בין שני הנקודות.
לכן, התנאים הם:

נוכל בקלות לפתור את המערכת המשוואות הזאת כדי לקבל:

לכן:

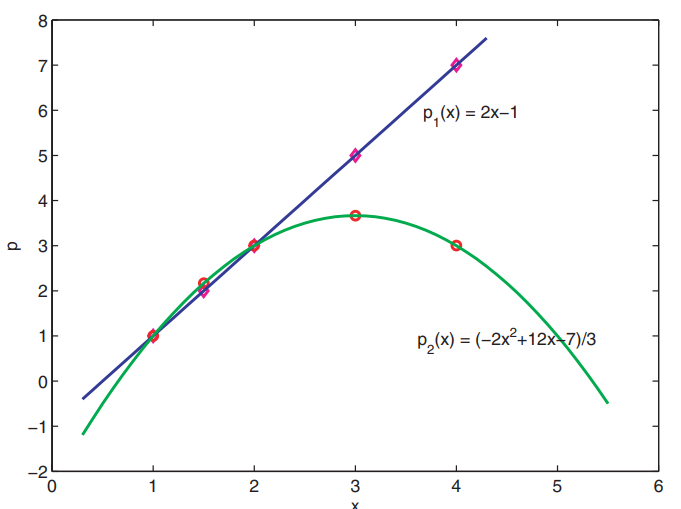
אם , והנקודות הן:

שתי הנקודות הראשונות הן אותן נקודות ממקודם. התנאים שלנו על האינטרפולנט:

הפתרון למערכת משוואות זו הוא:

ונקבל:

מטריצת ונדרמונד

נרשום את התנאים על האינטרפולנט הפולינומי בצורה מטריציונית:

המטריצה נקראת מטריצת ונדרמונד (), ויש לה דטרמיננטה מיוחדת:

ביטוי זה אומר שהדטרמיננטה של מטריצה זו הוא המכפלה של כל ההפרשים השונים ב-. לכן, כל עוד לכל , מתקיים . מכך נסיק שהמטריצה לא סינגולרית, יעני הפיכה. לפיכך, מתקיים המשפט הבא:

משפט:

לכל קבוצת נקודות כך ש- לכל , ישנו פולינום יחיד מסדר לכל היותר שמקיים את תנאי האינטרפולציה:

אינטרפולציית לגראנז’

נביט באינרפולנט שמקיים את התכונה הנחמדה . כלומר, המקדמים של הפולינום מקושרים ישירות לערכי הנקודות :

הפונקציות בסיס נתונות ע”י אינטרפולציית לגראנז’. באינטרפולציה זו אנו מגדירים את פולינומי לגראנז’ שהם פולינומים מסדר המקיימים:

כעת נוכל לרשום את האינטרפולנט:

אינטרפולנט זה אין מקיים את התנאים שמוצבים עליו:

דוגמה:

ניקח את אותם הנקודות מהדוגמה הקודמת:

נבנה את פולינומי לגראנז’ . לפי ההגדרה שלהם, נדרוש ש:

או בקיצור, נדרוש ש- ייתאפס בנקודות ו-. לכן הוא יהיה מהצורה:

נוסיף את הדרישה ש-. נקבל ש- , כלומר ש- . נציב:

באותו אופן נסיק ש:

אם נסכום את כל הפולינומי לגראנז’, נקבל את האינטרפולנט:

תכונות פולינומי לגראנז’

במקרה הכללי בו יש נקודות נתונות, הפולינומי לגראנז’ קיימים באופן יחיד, כי הם בעצמם אינטרפולציה פולינומית לנתונים מיוחדים. נוכל לרשום את הפולינום בצורה מפורשת:

קל יותר לראות למה זה נכון אם חוזרים על הדוגמה הקודמת ורואים שזה אחד לאחד הפעולות שביצענו.
במונה יש לנו פולינום ממעלה שמתאפס בכל הנקודות (מהנתונים) שמקיימות . במכנה, אנחנו בעצם מנרמלים את הפולינום הזה כך שנקבל

פולינום לגראנז’ כלשהו עבור .

חישוב האינטרפולנט

נראה כעת איך עלינו לחשב את האינטרפולנט בצורה אפקטיבית. נחשב ונסמן:

כאשר ל- אנו קוראים ערכי הנרמול. נשים לב שחישוב זה דורש פעולות.

עבור נקודה שלא נמצאת כחלק מהנתונים, נרצה לחשב את .
נסמן את המונה של כפונקציית עזר .

מה עם ?

ברור אז ש- הוא לא בדיוק המונה של . אל דאגה, אנחנו מתייחסים לזה. אנו עושים את זה כדי שנוכל להוציא את מסכימה שנראה בהמשך.

אז נוכל לרשום את פולינום לגראנז’ בצורה:

לפיכך, האינטרפולנט נתון ע”י:

חישוב זה הוא בסיבוכיות .

אלגוריתם: אינטרפולציית לגראנז’

1. בהינתן נתונים , נחשב את ערכי הנרמול: והמכפלות עבור .
2. בהינתן נקודה שאנו רוצים לחשב אותה, והיא לא חלק מהנתונים, נחשב:

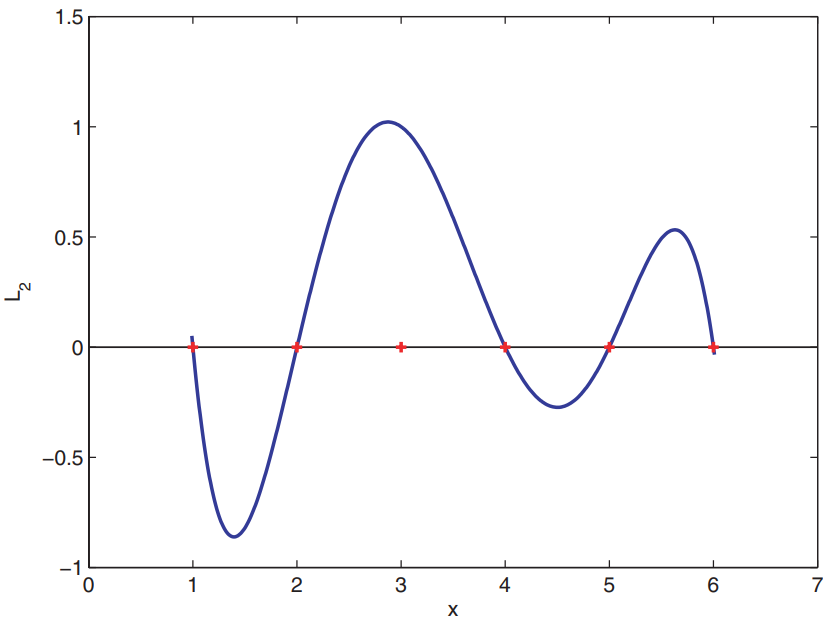
שגיאה באינטרפולציה פולינומית

נרצה לשער מהי השגיאה של ביחס לפונקציה האמיתית שמתארת את הנקודות . נבטא את השגיאה:

ניתן להראות כי השגיאה עבור אינטרפולציה כזאת היא שארית לגראנז’:

משפט:

אם היא אינטרפולציה של ב- נקודות , ול- יש נגזרות בקטע המכיל את נקודות אילו, אז לכל ישנה נקודה כך ש:

נשים לב כי אם המרווח שווה בין כל הנקודות:

אז מתקיים:

ולכן נקבל שהשגיאה שלנו חסומה:

---

תרגיל:
חשבו את פולינום האינטרפולציה של לגראנז’ מסדר שני עבור הנתונים:

הביאו את הפולינום לצורה:

פתרון:
לפי הנוסחה:

אז נחשב את פולינומי לגראנז’:

נקבל כי:

---

אינטרפולציה הפוכה

נרצה לפעמים לעשות את הפעולה ההפוכה מאינטרפולציה. כלומר, במקום למצוא את הערך עבור כלשהו, נרצה למצוא את הערך עבור מסוים.

למשל, עבור הנקודות:

נרצה לדעת עבור איזה נקבל ?
כל מה שעלינו לעשות זה להחליף בסימונים בין ל- בשיטת האינטרפולציה שלנו. אז עבור אינטפולציית לגראנז’:

הפולינומי לגראנז’ שלנו (נבחר ו-):

לכן:

→ קודם: NUM1_006הבא: NUM1_008 ←