| קורס | אלמנטים סופיים לאנליזה הנדסית |
|---|---|
| מספר קורס | 00350022 |
| סטודנט א’ | |
|---|---|
| שם | עידו פנג בנטוב |
| ת”ז | CLASSIFIED |
| דואר אלקטרוני | CLASSIFIED |
בעיה 1
שאלה 1
נתונה הבעיה:
כאשר:
לפי בעיות הולכה בזמן, לאחר טיפה העברת אגפים של (HW3.1):
נכפיל בפונקציית בוחן
נבצע אינטגרציה על כל התחום:
מאחר ויש לנו תנאי שפה מסוג דיריכלה בשתי הקצוות, מתקיים
נקרב את
הפרמטר
נוכל לרשום באופן מטריצי:
כאשר:
נקרב את האינטגרציה ע”י פונקציות בסיס לינאריות, כאשר המיפוי שלנו לתחום האינטגרציה
נרצה למצוא את
כאשר
לחישובים בהמשך, נצטרך לחשב עוד ערכים; היעקוביאן:
הנגזרת לפי
נשים לב ש:
לפי (HW3.4):
נקבל, באופן מטריצי:
באותו אופן על מטריצת המסה, מ- (HW3.3):
נבצע אינטגרציית גאוס בשתי נקודות. עבור התחום
לאחר הצבה נקבל:
שאלה 2
כמו ביישום לנוסח הרציף:
הקירוב עבור ההעתקה הדיסקרטית הוא:
כאשר
בסעיף קודם קיבלנו מערכת משוואות מהצורה:
לאחר העברת אגפים:
נרשום את אותה המשוואה לאחר צעד זמן
נכפיל את (HW3.5) במטריצת המסה מצד שמאל:
נציב ב-(HW3.8) את (HW3.6) ו-(HW3.7):
לאחר העברת אגפים:
נסמן:
ונסכם:
שאלה 3
ראינו כבר כי:
עבור כל אלמנט (נזכור כי
לכן המטריצות הגלובליות:
מאחר ויש לנו שני תנאי דיריכלה בשפות, אנחנו כבר יודעים ש-
פתרון עבור
נחשב את המטריצות
התנאי התחלה:
פתרון ב-
נקבל:
פתרון ב-
נקבל:
פתרון עבור
נחשב את המטריצות
פתרון ב-
נקבל:
פתרון ב-
נקבל:
פתרון עבור
עבור 4 אלמנטים, צעד הזמן הקריטי הוא
נחשב את המטריצות
פתרון ב-
פתרון ב-
שאלה 4 ו-5
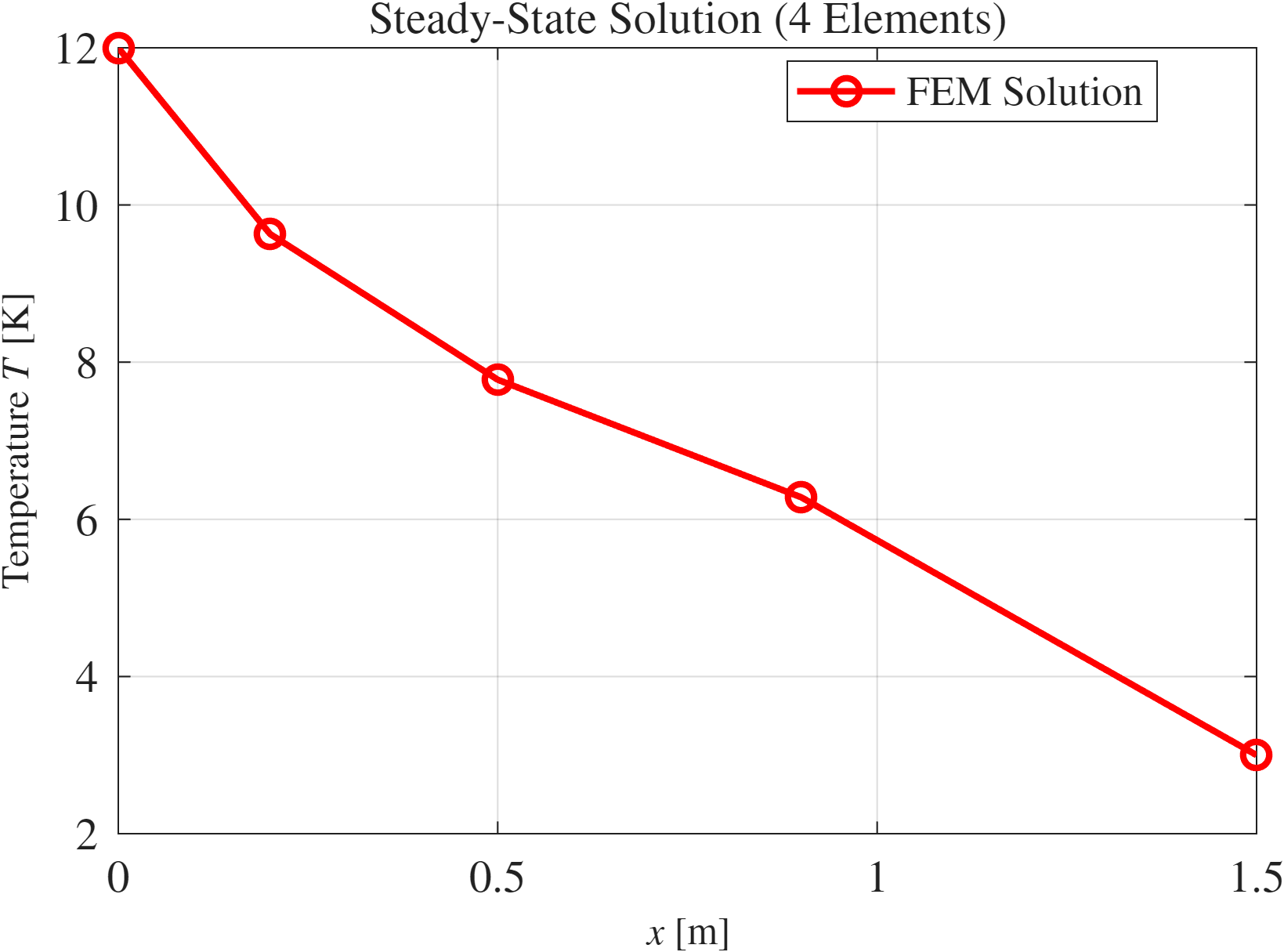
איור HW3.1: פתרון מצב מתמיד של בעיה (HW3.1) בארבעה אלמנטים.
שאלה 6
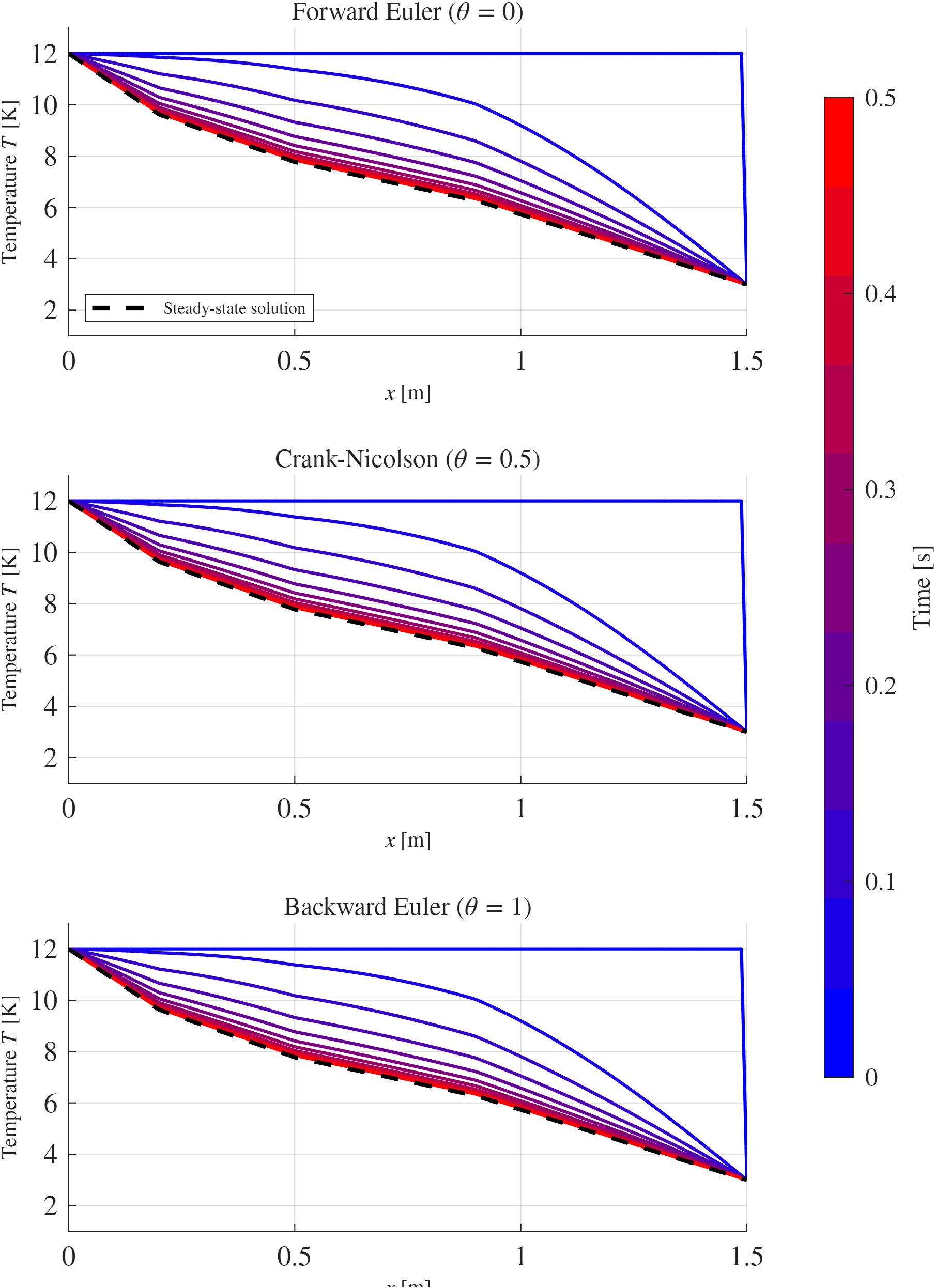
איור HW3.2: התפתחות בזמן של הפתרון עבור שיטות שונות עם
אלמנטים.
שאלה 7
נמצא כי צעד הזמן הקריטי הוא:
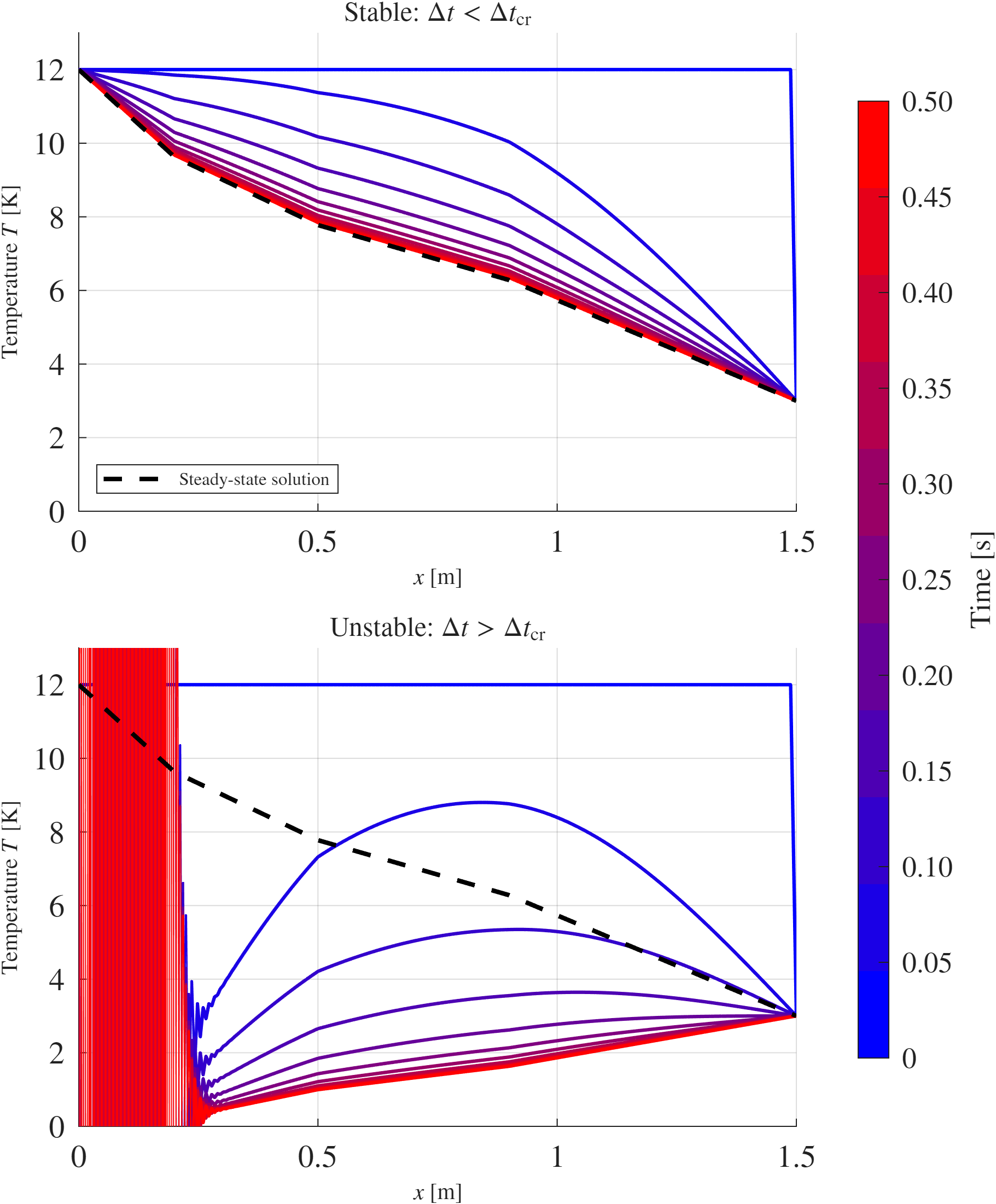
איור HW3.3: ניתוח יציבות עבור Forward Euler במקרה יציב ולא יציב.
