FLD1_010 ניתוק זרימה

→ קודם: FLD1_009

מבוא

תאוריית השכבת גבול בפרק הקודם נותנת פתרון יחסית מדויק כאשר מדובר בפלטה שטוחה, אבל היא לא עוסקת בתופעה מאוד חשובה: ניתוק זרימה.

זרימה סביב גליל בריינולדס (Van Dyke, 2008)

זרימה סביב גליל בריינולדס (Van Dyke, 2008)

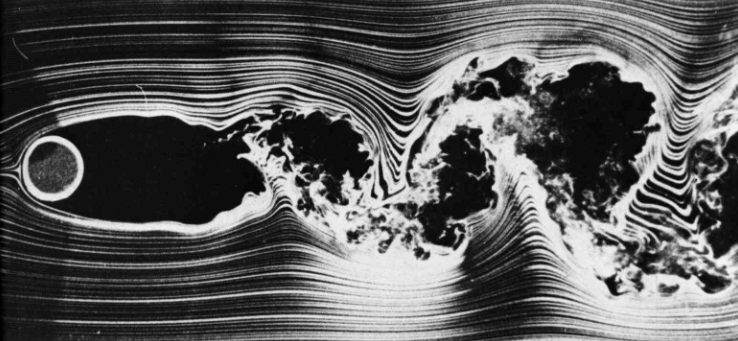
זרימה סביב גליל בריינולדס (Van Dyke, 2008)

פרנטל הראה שניתוק זרימה כזה נוצר כאשר הזורם מאבד הרבה מהמומנטום שלו בשכבת גבול והוא זורם כנגד לחץ עולה, . לגרדיאנט לחצים כזה נקרא גרדיאנט לחצים מנוגד (adverse pressure gradient) (הוא לא שלילי, ההפך!). למקרה ההפוך, בו , נקרא גרדיאנט לחצים רצוי (favorable pressure gradient).

הערה:

תרגומים שלי, לא מצאתי תרגום רשמי.

בזרימה צמיגה, כיוון הזרם הוא מלחץ גבוה ללחץ נמוך (גרדיאנט לחצים רצוי, שלילי), בעוד בזרימה פוטנציאלית הזרימה עשויה לזרום בכיוון ההפוך לגרדיאנט הלחץ. לכן, בעוד הזרימה הפוטנציאלית החיצונית תמשיך לזרום באותו הכיוון, בשכבת גבול תהיה התנגדות שנובעת מהצמיגות. בתנאים אלו, הזרימה בתוך השכבת גבול עלולה להאט, לעצור, או לשנות כיוון.

קריטריון להתנתקות

נוכל לקשר בין גרדיאנט הלחצים לנגזרת השנייה של לפי . ממשוואות שכבת הגבול, על הקיר (בו ):

נסדר ונקבל:

לכן, בגרדיאנט לחצים חיובי (בו תהיה התנתקות), הנגזרת השנייה של המהירות ליד הקיר חיובית. אנחנו גם יודעים שבקצה שכבת הגבול (), הנגזרת השנייה חייבת להיות שלילית כדי להתמזג בצורה חלקה עם הזרימה החיצונית .
לפיכך, אם הנגזרת השנייה עוברת דרך הערך אפס בשלב מסוים (נקודת פיתול) לאורך שכבת הגבול, אז באיזשהו גובה גרדיאנט הלחצים משנה סימן, ותהיה התנתקות.

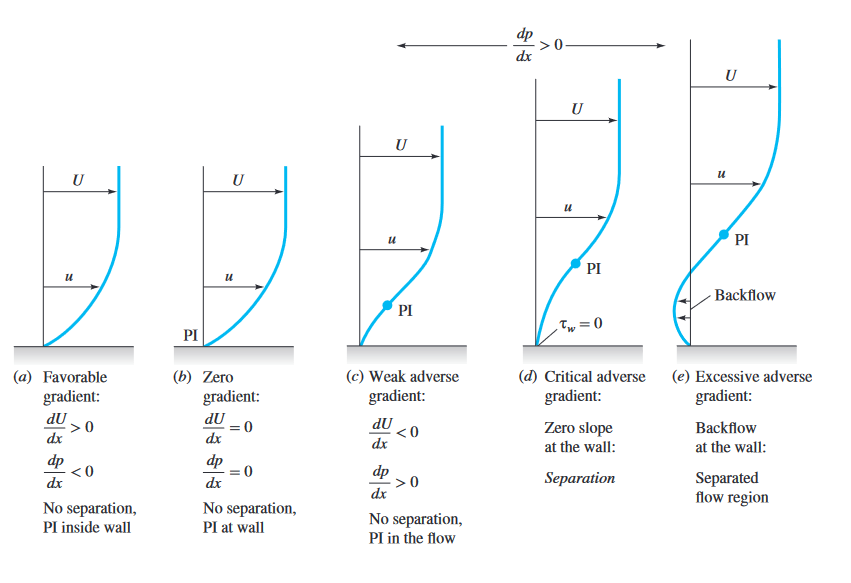
אפקט גרדיאנט הלחצים על פרופילי מהירות של שכבת גבול. (White & Xue, 2021)

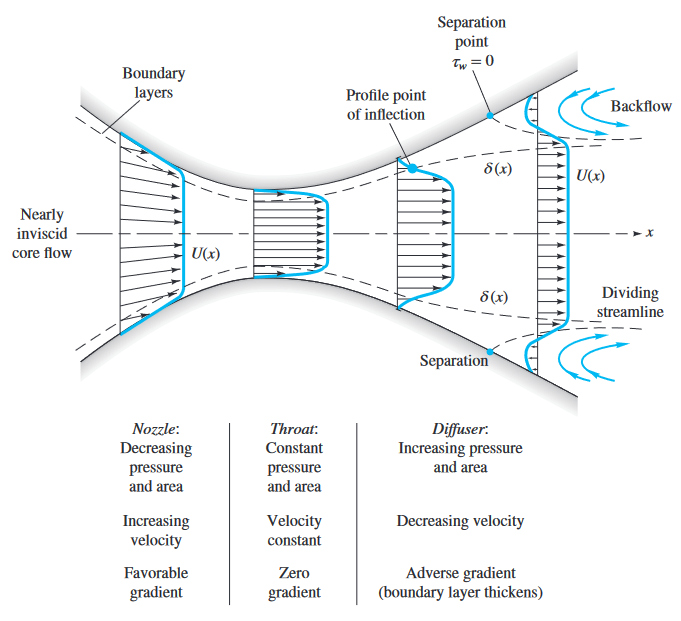
בנחיר ומאט למשל, גרדיאנט הלחצים שלילי בנחיר, וחיובי ליד הקיר במאט, מה שגורם לניתוק, ואפילו זרימה בכיוון ההפוך ליד הקיר.

בקורס זה, למען פשטות, הקריטריון שלנו להתנתקות מפושט ל:

כלומר, אם שינה סימן באיזשהו , אז ישנה התנתקות. יותר מכך, ב- בו שינוי סימן זה קורה ספציפית ב-, אז נקודה זו היא נקודת ההתנתקות - הנקודה בה ההתנתקות מתחילה:

שיטת פולהאוזן

לפני שנראה כיצד נוכל להפעיל את קריטריון זה על בעיות שונות, עלינו להכליל טיפה את התאוריית שכבת גבול שעסקנו בה. עד כה עסקנו בפלטה שטוחה, בה בחיים לא תתקיים התנתקות כי לא יתפתח בה גרדיאנט לחצים מנוגד. כדי לבחון גאומטריות יותר מסובכות, נצטרך למצוא קשר כללי יותר בין עובי שכבת הגבול לפרופיל המהירות החיצוני .

מאינטגרל פון קרמן, אנו יודעים ש:

אבל זה כשהנחנו שמדובר בפלטה שטוחה וזרימה מציפה קבועה (). אם לא היינו מניחים את הנחות אלו (כלומר, אם לא קבוע), אינטגרל פון קרמן מקבלת את הצורה:

אם אנו יודעים את פרופיל המהירות, נוכל למצוא את ו-, להציב במשוואה זו, ואז נקבל קשר בין עובי שכבת הגבול ומהירות חיצונית , שנכונה גם אם לא מדובר בפלטה שטוחה!

לפי שיטת פולהאוזן, אנו מניחים שפרופיל המהירות הוא פולינום מסדר חמישי:

כאשר .

מתנאי השפה על שכבת הגבול, נוכל למצוא ש:

כאשר מוגדר כ:

ל- זה אנו קוראים פולינום פולהאוזן, והוא מתאר את פרופיל המהירות בשכבת גבול, בצורה מנורמלת ל-.

עם פרופיל מהירות זה, אנו יכולים למצוא את עובי הזזה ועובי שכבת מומנטום:

נותר למצוא את .
הגדרת המאמץ גזירה היא:

מהגדרת , נסיק כי , כך שלפי כלל השרשרת:

מהגדרת , נסיק כי , ולכן:

נשים לב כי:

נציב בחזרה בהגדרת :

כאשר נציב את פרופיל מהירות זה ב-(1), עם עוד כל מיני קירובים והזנחות, נקבל ש:

קיבלנו קשר בין עובי שכבת הגבול ומהירות חיצונית , שנכונה גם אם לא מדובר בפלטה שטוחה.

מימוש הקריטריון בשיטת פולהאוזן

פולינום פולהאוזן הוא:

הקריטריון להתנתקות במונחים של הוא פשוט:

נציב את :

לכן, ההתנתקות מתרחשת עבור:

נזכור ש:

כלומר, עלינו למצוא את כדי למצוא איפה מתרחשת ההתנתקות. פיתחנו קשר בסוף חלק קודם בין ל-. נוכל להגדיר את הפרמטר

להציבו בקשר זה, ולאחר המון פיתוחים אלגבריים וקרובים, נקבל:

ניתן להראות שכאשר , אז . כלומר, בנקודת הניתוק, מתקיים:

כעת, כדי למצוא את נקודת הניתוק בהינתן פילוג המהירות החיצוני לשכבת גבול , נוכל להציב את פילוג מהירות זה בביטוי שקיבלנו עבור , ולמצוא מתי .

לפעמים, כמו בשאלה 2, עובי שכבת הגבול יהיה נתון, ונוכל פשוט להציב ישירות בביטוי בסוף חלק קודם כדי למצוא ביטוי ל-, ואז להציב את .

תרגילים

כוח אופקי פועל על גבי פלטה מלבנית בעלת אורך ועומק (לתוך הדף). כתוצאה מכך, הפלטה זזה במהירות קבועה . הפלטה נתונה לזרימה אחידה ובנוסף, ישנה הזרקה/יניקה של זורם במהירות של בטווח . כתוצאה מכך, עובי שכבת הגבול הופכת לקבועה באזור ההזרקה.

הנח כי אין מאמץ על החלק התחתון של הפלטה התחתונה.
הנח פילוג מאמץ גזירה אחיד עבור .

שאלה 1

סכמת הבעיה

סעיף א’

צייר באופן סכמתי את פרופיל המהירות בכיוון בתחום .

פתרון:

פרופיל המהירות

סעיף ב’

השתמש בפרופיל הזרימה המקורב , כאשר .
כתוב את כל תנאי השפה הרלוונטיים על מנת למצוא את מקדמי הפולינום.

פתרון:
לפי תנאי שפה על שכבות גבול, נשתמש רק ב:

1. אי החלקה:
2. מעצם הגדרת השכבת גבול:
3. השפה העליונה של השכבת גבול היא שפה חופשית (אין עליה כוחות גזירה), ולכן:
4. בנוסף, נוכל להשתמש גם בעובדה שהפלטה נעה במהירות קבועה, כך ש: הכוחות היחידים שפועלים זה הכוח הנתון וכוח הגרר על הפלטה, כך ש:

נתחיל להציב:

עבור תנאי השפה השלישי נצטרך לגזור את לפי . נשים לב שמהגדרת מתקיים, כך שלפי כלל השרשרת:

מהגדרת , נסיק כי , ולכן:

מהתנאי שפה השלישי, , ולכן:

נציב את שמצאנו גם בתנאי ההתחלה הרביעי:

מארבעת המשוואות נוכל למצוא את ארבעת המקדמים .
נקבל:

סעיף ג’

מצא את כתלות בפרמטרים של הבעיה .

פתרון:
לפי אינטגרל פון קרמן:

במקרה שלנו, , כך שרוב הנגזרות מתאפסות, או שנוכל פשוט להוציא החוצה:

לפי שיטת פולהאוזן מתקיים . במקרה שלנו, כיוון ש- מוגדר כ- , ו- קבוע, נוכל לומר כי , ולכן:

אבל גם קבוע, כך שגם מתקיים . נציב באינטגרל פון קרמן:

מסעיף קודם אנו יודעים ש- . בנוסף, מוגדר להיות , כך ש:

שאלה 2

פלטה שטוחה נתונה לזרימה אחידה במהירות . ישנה הזרקה/יניקה במהירות . נתח את החלק העליון של הפלטה.
פרופיל הזרימה המקורב ע”י פולינום פולהאוזן על גבי הפלטה הוא:

כאשר פרמטר פולהאוזן הינו:

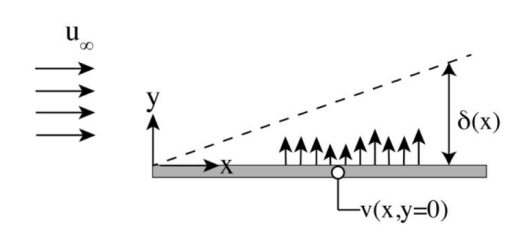
סכמת הבעיה

סעיף א’

מהם התנאים ליצירת שכבת גבול על גבי הפלטה?

פתרון:
נדרוש שהזרימה תהיה אינרציאלית .

סעיף ב’

השתמש באינטגרל פון קרמן עבור שכבות גבול כדי למצוא מה צריכה להיות מהירות ההזרקה כדי שעובי שכבת הגבול יהיה .

פתרון:
לפי משוואת פון קרמן אנו יודעים ש:

נוכל לפי אותם הפיתוחים בשיטת פולהאוזן להגיע לביטוי הארוך שמופיע בסוף החלק. במקרה שלנו מתקיים, אז רוב האיברים מתבטלים (כולל ):

נדרוש ש- , ואז נקבל:

סעיף ג’

האם תתרחש התנתקות עבור פרופיל הזרימה שלעיל? אם כן הסבר היכן. אם לא, הסבר מדוע.

פתרון:
אנו יודעים ממימוש הקריטריון בשיטת פולהאוזן תהיה התנתקות כאשר . מהגדרת :

אבל, קבוע, כך ש- , ולא תתרחש התנתקות.

סעיף ד’

כעת פרופיל המהירות החיצונית משתנה ל- , אך עובי שכבת הגבול נותר ללא שינוי . האם תתרחש התנתקות כעת? אם כן, היכן?

פתרון:
הפעם, מקיים:

נמצא מתי :

כלומר, תתרחש התנתקות ב-.

→ קודם: FLD1_009