HTF1_005 מבוא להסעה

→ קודם: HTF1_004הבא: HTF1_006 ←

מבוא

עד כה עסקנו בבעיות הולכה מהסוג:

ופתרנו את משוואות אלו כדי למצוא את פילוג הטמפרטורה, ומשם את קצב מעבר החום. הייחוס היחידי שלנו להסעה היה כאשר התחשבנו בו כתנאי שפה למוצק עליו אנו כותבים את המשוואה. נזכיר כי הסעה כוללת את המעבר אנרגיה גם ע”י תנועה מקרוסקופית של הזורם, וגם ע”י תנועה רנדומלית של החלקיקים.

נקודה מעניינת בהסעה היא שהאופן הסעה של מסה אנלוגית לאופן הסעה של מעבר חום. כלומר, כמו בזרימה, נעסוק כאן בשכבות גבול, זרימה טורבולנטית שכבתית (למינרית), זרימה מול פלטה שטוחה וכו’.

שכבות גבול

עיקרון השכבות גבול הוא חיוני להבנת ההסעה של מסה וחום בין משטח וזורם. לכן, נעבור בקצרה על שכבת גבול מהירות, לפני שנעבור לשכבת גבול תרמית.

שכבת גבול מהירות

כאשר זרימה מציפה פוגשת בפלטה שטוחה, על הפלטה עצמה, הזרם נעצר - לפי תנאי האי-החלקה. חלקיקים אלו לאחר מכן פועלים כנגד המהירות של החלקיקים בשכבה מעליהם, וחלקיקים אלו מאטים גם כן את החלקיקים בשכבה מעליהם - מה שיוצר בסוף שכבת גבול.

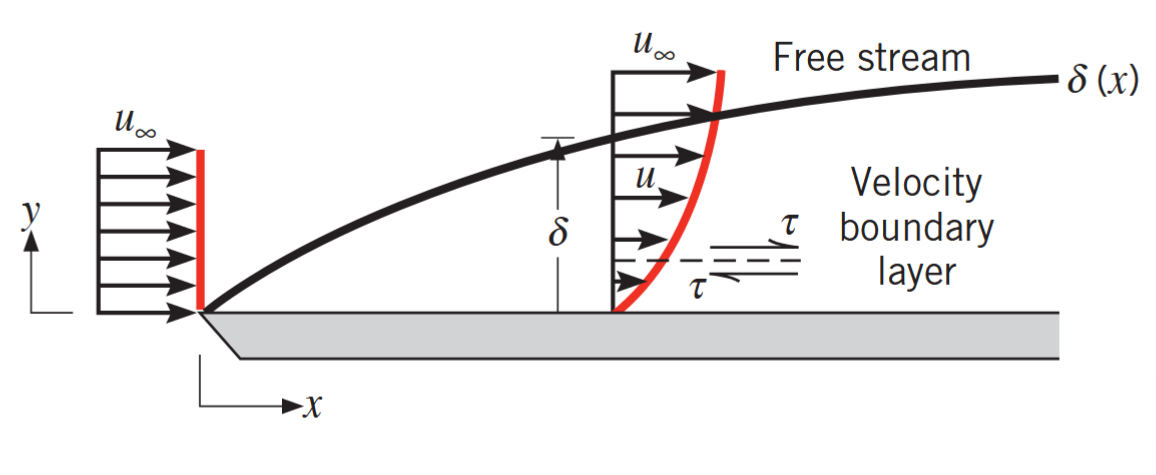
התפתחות שכבת גבול מהירות על פלטה שטוחה. (Bergman & Lavine, 2017).

מקדם החיכוך המקומי על הפלטה מוגדר בעזרת המאמץ גזירה :

כאשר מאמץ הגזירה מוגדר בעזרת הצמיגות הדינמית של הזורם:

כדאי לעבור על שאר הנושאים בשכבת גבול בזרימה (הנחות לשכבת גבול, המשוואות, הפתרונות למשוואות וכו’) לפני שעוברים לשכבת גבול תרמית.

שכבת גבול תרמית

כמו ששכבת גבול מהירות מתפתחת כאשר יש זרימת זורם על משטח, שכבת גבול תרמית מתפתחת אם יש הפרש טמפרטורות בין הזרימה המציפה של הזורם והמשטח. נביט באיור הבא:

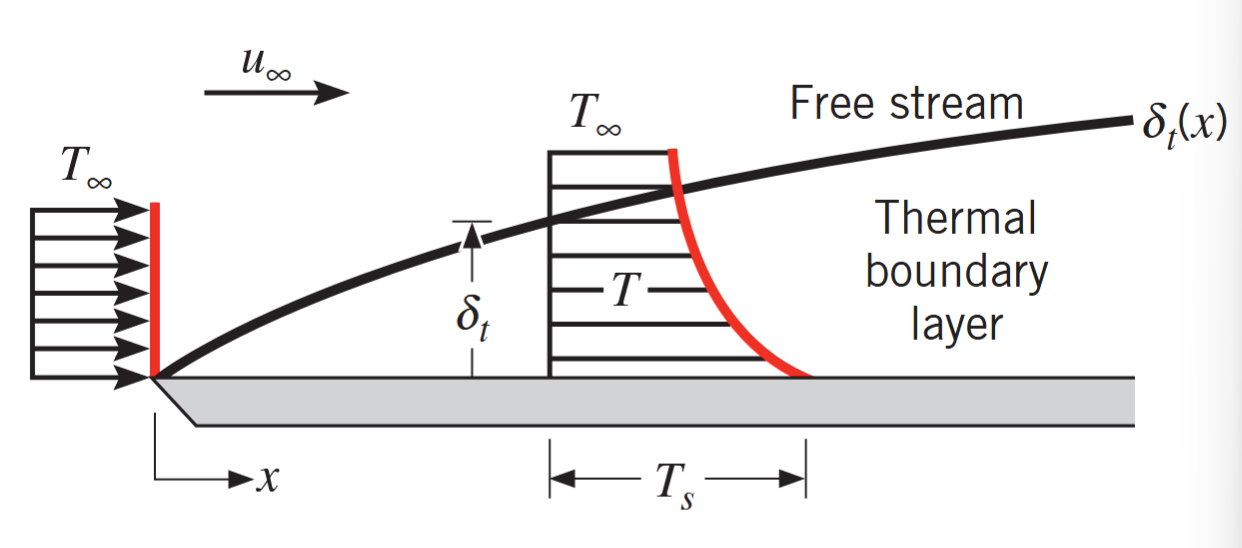
שכבת גבול תרמית המתפתחת על משטח איזותרמי. (Bergman & Lavine, 2017).

בדופן הלוח, פרופיל הטמפרטורה הוא אחיד, עם . אבל, החלקיקי זורם שבאים במגע עם הפלטה מגיעים לשיווי משקל תרמי בטמפרטורת הפלטה. משכבה זו, החלקיקים מחליפים אנרגיה עם השכבות מעליהם, מה שיוצר גרדיאנט טמפרטורות. לאזור זה בזורם בו קיים גרדיאנט טמפרטורות קוראים שכבת גבול תרמית, והעובי שלה, , מוגדר כהערך של עבורו .

נפתח כעת את הקשר בין התנאים בשכבת גבול זו ומקדם ההסעה . בכל מרחק מהדופן, השטף החום המקומי ניתן לחישוב מחוק פורייה על הנוזל ( עבור fluid) ב-:

כאשר הוא עבור surface. בהמשך נוריד את סימון זה וניקח אותו כמובן מאליו.
בשפה, אין תנועת זורם, והמעבר חום מתרחש אך ורק ע”י הולכה. מחוק הקירור של ניוטון:

ולכן:

לפיכך, התנאים בשכבת גבול, המשפיעים על גרדיאנט הטמפרטורה , קובעים את הקצב מעבר חום מהשפה. מאחר ו- הוא קבוע (לא תלוי ב-), כאשר גודלת עם , גרדיאנטי הטמפרטורות בשכבות גבול יורדים עם גדילת . לכן, ו- קטנים עם גדילת .

זרימה טורבולנטית ולמינרית

בזרימה התמקדנו באזור הלמינרי של שכבות הגבול, אבל חשוב לנו כאן להתייחס גם לשכבת הגבול הטורבולנטית.

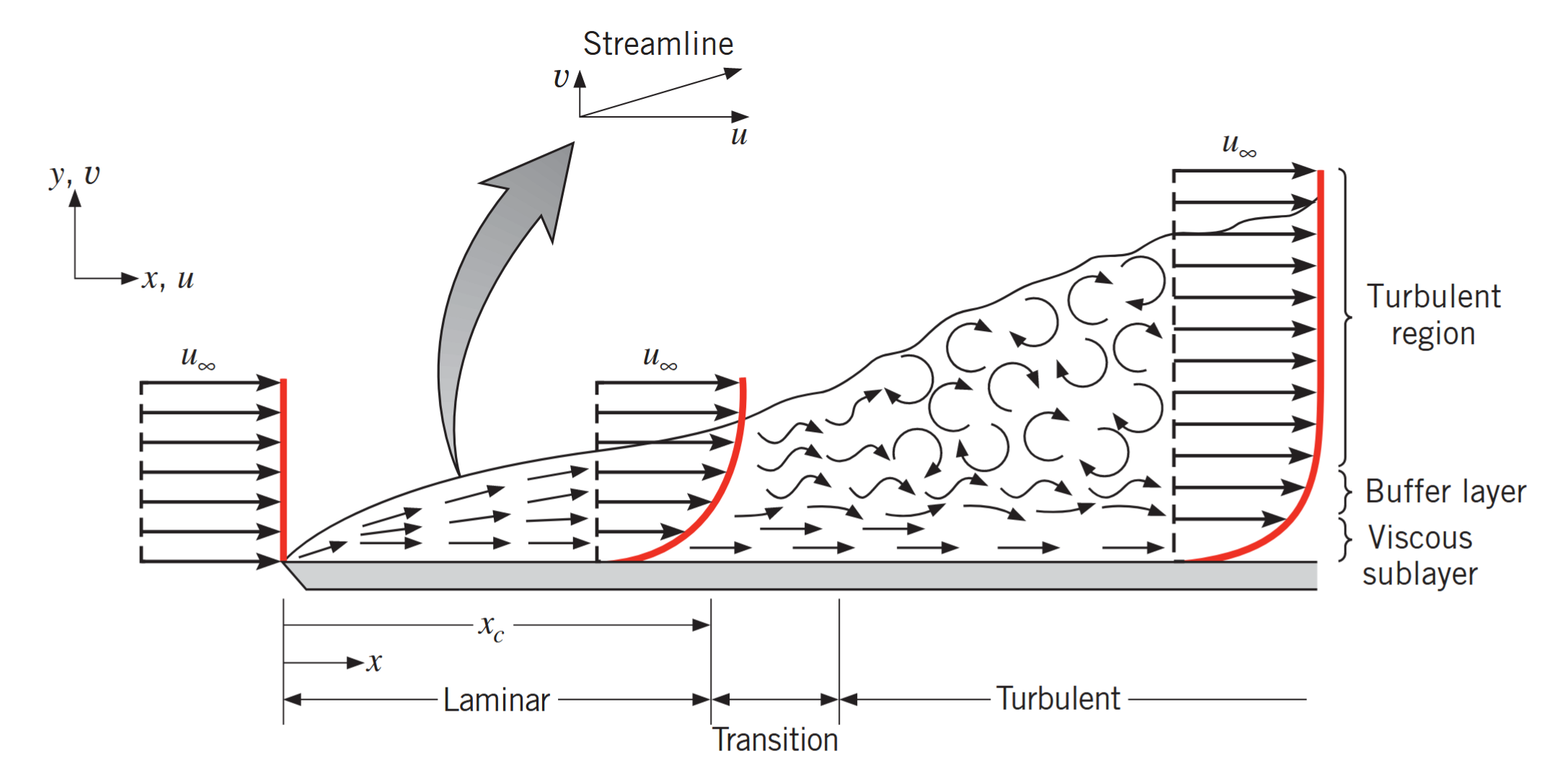
התפתחות שכבת גבול מהירות על פלטה שטוחה. (Bergman & Lavine, 2017).

בשכבת גבול הלמינרית, הזרם מסודר באופן שכבתי וניתן לזהות קווי זרם לאורכם החלקיקי זורם נעים. הסדר הזה ממשיך עד שמגיעים ל-אזור מעבר, שלאורכו מתרחש מעבר מזרימה למינרית לטורבולנטית.
הזרם בשכבת גבול הטורבולנטית, בכללי, הוא מאוד מפוזר, והוא מאופיין בתנועה תלת ממדית רנדומלית. הערבוב בתוך השכבת גבול לוקח זורם במהירות גבוהה לשפת המוצק ומעביר זורם במהירות נמוכה הרחק יותר אל הזרימה המציפה.

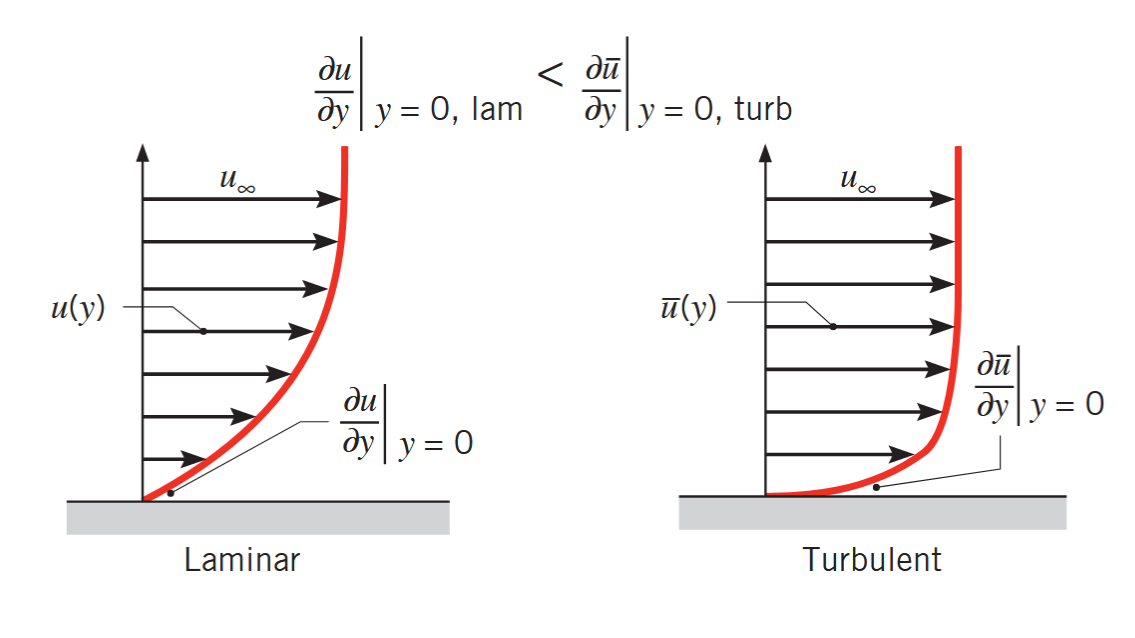
השוואה בין פרופיל זרימה של שכבת גבול למינרית וטורבולנטית עבור אותה הזרימה המציפה. מאחר והמהירות משתנה בזמן בזרימה טורבולנטית, המהירות הממוצעת, , משורטטת בגרף. (Bergman & Lavine, 2017).

כדי לחשב האם השכבת גבול טורבולנטית או למינרית, נהוג להניח שהמעבר מתרחש במיקום קריטי כלשהו ( עבור critical), שהוא נמצא ע”י מספר ריינולדס קריטי. לזרימה על פלטה שטוחה, נע בין ל- כתלות בחספוס המשטח ורמת הטורבולנציה של הזרימה המציפה. בקורס נניח ערך של

אלא אם כן מצוין אחרת.

משוואות שכבת הגבול

בזרימה חישבנו את עובי שכבת הגבול, המקדם חיכוך ועוד פרמטרים נוספים המאפיינים את שכבת הגבול בעזרת משוואות שכבת הגבול. הגענו במהלך הדרך למאזן תנע קווי בכיוון מהצורה (במצב מתמיד):

באותו אופן, אנו יכולים גם לפתח את המשוואה הבאה משימור אנרגיה:

הביטויים בצד שמאל מתארים את סך הקצב בו אנרגיה תרמית עוזבת את נפח הבקרה כתוצאה מתנועה של זורם. הביטוי הראשון בצד ימין מתאר את סך האנרגיה התרמית הנכנסת כתוצאה מהולכה בכיוון . הביטוי האחרון בצד ימין הוא האנרגיה שנותרה מדיסיפציה תרמית.

בדרך כלל מזניחים איבוד לחיכוך בתוך הזרם, כי הוא בדרך כלל מסדר גודל , ולכן נישאר עם:

^eq-*6-29

משוואות שכבת הגבול המנורמלות

כמו בזרימה, נוח לנו לעבוד עם גדלים חסרי ממד, ולכן נסמן:

תנאי שפה במונחים של :

נציב לתוך משוואת שימור האנרגיה (*6.29):

כאשר:

הגדרה: מספר פרנדטל

הביטוי נקרא מספר פרנדטל (Prandtl), והוא מוגדר כ:

כאשר הוא ההולכה התרמית של ה-זורם ( עבור fluid). מספר זה בעצם מתאר את היחס בין כמה מהר התנע מתפזר, וכמה מהר הטמפרטורה מתפזרת.

משימור האנרגיה נסיק שהפתרון למשוואה (IH6.36) הוא מהצורה:

מהגדרת מקדם ההסעה, משוואה (IH6.5):

במונחים חסרי ממד:

ביטוי זה מרמז על תלות במספר חסר ממד הנקרא:

הגדרה: מספר נוסלט

מספר נוסלט מוגדר באופן הבא:

מספר זה שווה לגרדיאנט הטמפרטורה החסר ממד בשפה, והוא מספק מידה לכמות המעבר חום בהסעה המתרחש בשפה.

ממשוואה (IH6.47), נסיק ש-עבור גאומטרייה נתונה:

כמו ש- הוא המקדם חיכוך של השכבת גבול מהירות, מספר נוסלט גם מתפקד כסוג של “מקדם חיכוך” לשכבת גבול התרמית. ממשוואה (IH6.49), עבור גאומטרייה נתונה, מספר נוסלט חייב להיות פונקציה של ו-. אם אנו יודעים את פונקציה זו, נוכל לחשב את ערכי לזורמים שונים וערכים שונים של ו- (אורכים ומהירויות אופייניים). במידה ו- ידוע, נוכל לחשב את המקדם להסעה המקומי , ומכך למצוא שטף החום המקומי. מאחר והמעבר חום ה-ממוצע מחושב ע”י אינטגרציה לאורך כלל השטח פנים של הגוף, הוא לא תלוי ב-, ואז התלות של המספר נוסלט ה-ממוצע הופכת להיות:

אנלוגיות שכבות גבול

כמהנדסים, עיקר העניין שלנו בשכבות גבול הוא במציאת המספרים החסרי ממד המאפיינים אותם כמו ו-. בעזרת מספרים אלו אנו יודעים לחשב את המאמץ גזירה והקצבי מעבר חום בהסעה. לכן, ביטויים המקשרים בין ו- יכולים להיות מאוד שימושיים עבורנו. לביטויים אלו אנו קוראים אנלוגיות שכבות גבול.

אנלוגיית ריינולדס

מטבלה 6.1 ניתן לראות שעבור ו- , משוואות (IH6.35) ו-(IH6.36) הן מאותה הצורה. עבור פלטה שטוחה הנתונה לזרימה מציפה, מתקיים . ביחד עם , גם משוואות (IH6.38) ו- הן מאותה הצורה. נסיק מכך ש:

נגדיר עוד מספר חסר ממד:

הגדרה:

מספר סטנטון (Stanton) מוגדר כ:

וכעת נוכל לרשום את (IH6.66) בצורה:

משוואה זו נקראת אנלוגיית ריינולדס, והיא מקשרת בין השכבת גבול מהירות לשכבת הגבול התרמית. משוואה זו נכונה עבור המקרה של ו- , אבל ניתן להכליל אותה למקרים נוספים.
קיים קשר אמפירי (מבוסס על ניסויים) שאומר שעבור , מתקיים מה שנקרא אנלוגיית ריינולדס המתוקנת:

פלטה שטוחה תחת זרימה מציפה

למרות פשטותה, זרימה מציפה על פלטה שטוחה מתרחשת במספר רב של בעיות הנדסיות. כפי שכבר הזכרנו, זרימת למינרית מתחרשת בדופן הפלטה, ומתפתחת לזרימה טורבולנטית במיקום כלשהו, עבורו מתקבל מספר ריינולדס קריטי .

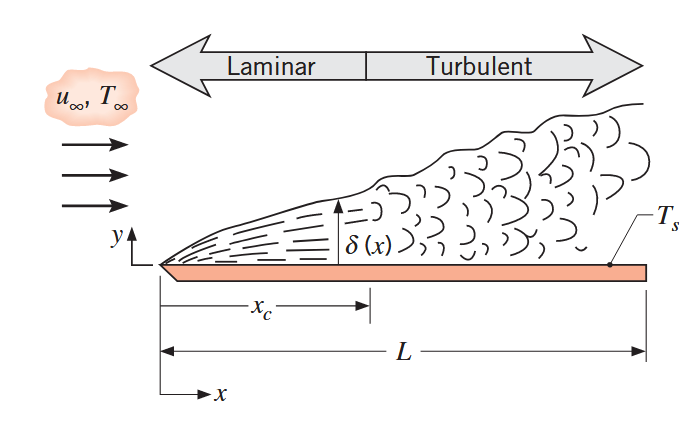
זרימה מציפה על פלטה שטוחה. (Bergman & Lavine, 2017).

ננתח את הזרימות השונות מבחינת מהירות וטמפרטורה בעזרת פתרון בלסיוס:

זרימה למינרית בפלטה שטוחה

מפתרון בלסיוס לזרימה, עובי שכבת הגבול הוא

ומקדם החיכוך:

הממוצע:

באותו אופן, ניתן למצוא בעזרת פתרון בלסיוס את :

והממוצע:

נזכור כי מספר פרנדטל מתאר את היחס בין יעילות המעבר אנרגיה ומומנטום ע”י דיפוזיה בשכבת המהירות לבין יעילות המעבר אנרגיה ומומנטום ע”י דיפוזיה בשכבה התרמית. לכן, נצפה שתהיה לו השפעה לקשר בין עובי שכבת גבול המהירות לעובי שכבת הגבול התרמית.
ואכן, מהשוואה בין הפתרונות, עבור פלטה שטוחה:

זרימה טורבולנטית בפלטה שטוחה

עבור זרימה טורבולנטית אין תקווה למצוא פתרון באופן אנליטי, ולכן פונים לניסויים.

עבור זרימה טורבולנטית ישרה, כאשר , התקבל מניסויים, עם דיוק של , ש:

עובי שכבת הגבול ניתן לקירוב כ:

מהשוואת ביטויים אלו למשוואות המתאימות בזרימה למינרית, (IH7.19) ו-(IH7.20), נסיק כי גדילת השכבת גבול באזור הטורבולנטי הרבה יותר מהירה, והירידה במקדם החיכוך יותר מתונה. עבור זרימה טורבולנטית, התפתחות שכבת הגבול מושפעת משינויים רנדומליים בזורם, ולא מדיפוזיה מולקולרית. לכן, קצב גדילת השכבת גבול התרמית לא תלוי ב-, ונוכל להשתמש במשוואה (IH7.35) כדי לחשב גם את עובי השכבת גבול התרמית, .

מאנלוגיית ריינולדס ומשוואה (IH7.34), מספר נוסלט המקומי הופך להיות:

והממוצע:

זרימה מעורבת

עבור זרימה למינרית המתרחשת לכל אורך הפלטה, ניתן להשתמש במשוואות (IH7.29) ו-(IH7.30) לחישוב המקדמים הממוצעים. למעשה, גם אם מתרחש מעבר לזרימה טורבולנטית בסוף הפלטה, למשל בטווח , משוואות אלו עדיין יכולות לשמש קירוב מספיק טוב לחישוב המקדמים. אבל, אם המעבר מתחרש מספיק רחוק מקצה הפלטה, נצטרך לקחת בחשבון את המקדמים הממוצעים גם של הזרימה הטורבולנטית וגם של הזרימה הלמינרית.

במקרה המעורב, נחשב את המקדם מעבר חום בהסעה הממוצע באופן הבא:

כאשר, לפי משוואות (IH7.23) ו-(IH7.36):

מאינטגרציה נקבל:

כאשר משוואה זו תקפה כאשר וגם , ו- הוא קבוע שנקבע ע”י מספר ריינולדס הקריטי באופן הבא:

באותו אופן ניתן לחשב כוח חיכוך ממוצע. אם :

לשכבת גבול שהיא טורבולנטית לחלוטין, מתקיים , ולכן . ניתן לקבל סיטואציה כזאת אם מניחים איזה חפץ מחוספס בדופן הפלטה שיזניק את הטורבולנציה. עבור הקירוב , מתקיים .

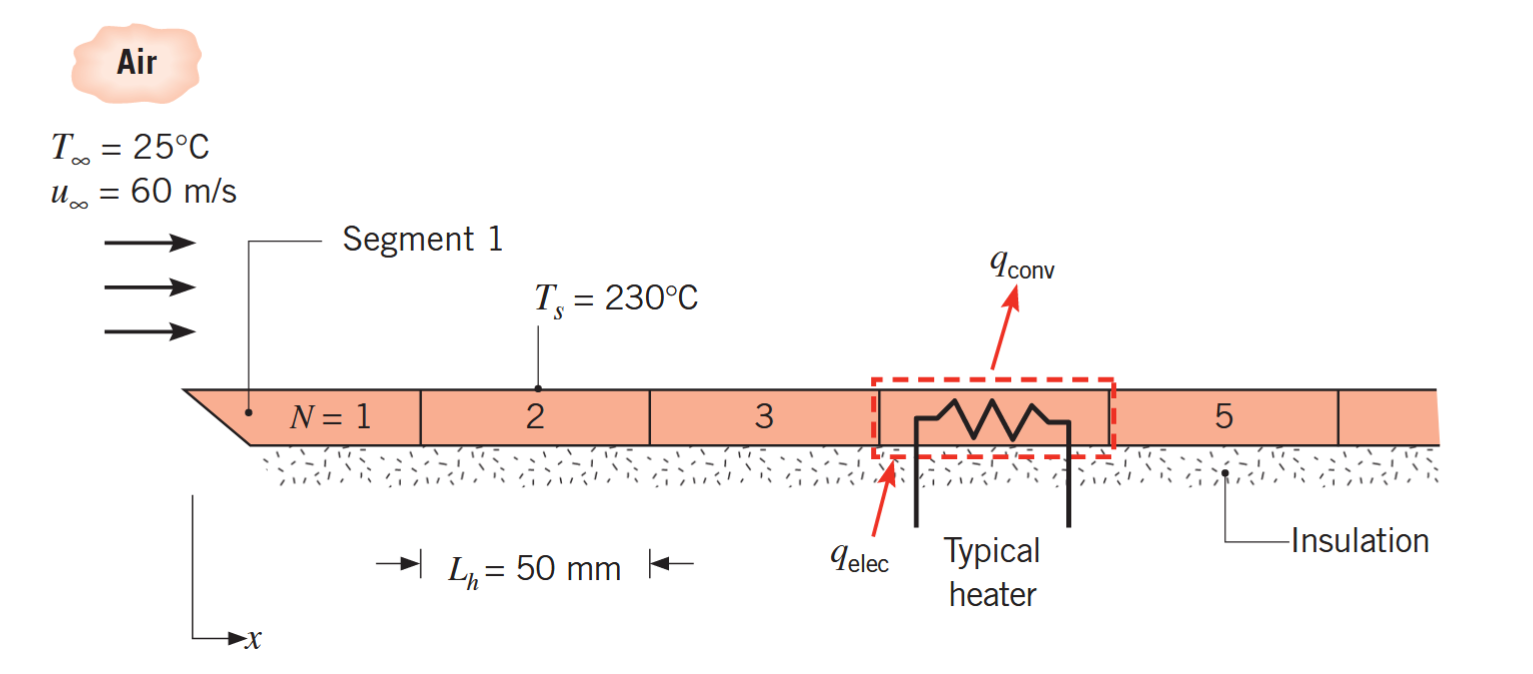
דוגמה: 7.2 בספר

נתון לוח שטוח ברוחב מטר המוחזק בטמפרטורה אחידה וקבועה ע”י סדרת מחממים באורך . הלוח חשוף לאוויר במהירות ובטמפרטורה .

איזה מהמחממים דורש הספק מקסימאלי וכמה?

פתרון:
עבור אוויר, מטבלה A.4 בספר:

מספר ריינולדס לחלק המחמם הראשון, באורך :

במידה וריינולדס הקריטי הוא , נסיק שהמעבר לטורבולנציה יתרחש ב:

נסיק שהמעבר מתרחש במחמם החמישי. נסיק שישנם שלוש אפשרויות למחמם קריטי הדורש את ההספק המקסימלי:

1. המחמם הראשון
2. המחמם החמישי
3. המחמם השישי

בכללי, עבור המחמם ה--י, ההספק חום צריך להיות:

לפי שימור אנרגיה, ההספק הדרוש למחמם ניתן לחישוב ע”י חיסור קצב איבוד החום של ה- מחממים הראשונים מקצב איבוד החום של כלל ה- מחממים. אם מגדירים את כמקדם החום להסעה הממוצע למחממים עד , ההספק חום הדרוש למחמם שווה לקצב מעבר החום בהסעה מהמחמם, שניתן לביטוי כ:

ממשוואות (1) ו-(2) נקבל:

עבור המחמם הראשון, מספר נוסלט:

ולכן מקדם מעבר החום:

עבור המחמם החמישי, לפי משוואה (IH7.38):

לכן המקדם מעבר חום במחממים עד :

את הערך של נוכל למצוא באותו אופן שמצאנו את , ואז נמצא כי:

ממשוואה (3):

באותו אופן מחשבים עבור ונקבל בסוף:

מאחר ו-, נסיק שהמחמם השישי ידרוש הכי הרבה הספק חום, שהוא:

אורך התחלה ללא חימום

מספרי נוסלט לעיל תקפים למקרים בהם טמפרטורת השפה אחידה. אבל,
יש מספר מקרים יוצאי דופן שנפוצים גם הם, כמו למשל הקיום של אורך התחלה ללא חימום () במעלה הזרם של פלטה מחוממת (). כפי שמוצג באיור הבא, השכבת גבול מהירות מתחילה ב-, בעוד השכבת גבול התרמית מתחילה ב- :

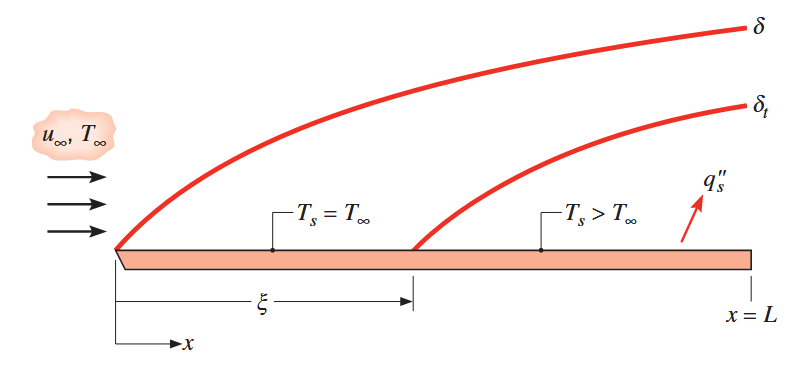
פלטה שטוחה במקביל לזרם עם אורך התחלה ללא חימום. (Bergman & Lavine, 2017).

לכן, אין מעבר חום ב- . ניתן להראות שעבור זרימה למינרית, מספר נוסלט המקומי הוא:

כאשר נתון ע”י משוואה (IH7.23). גם ב- וגם ב- האורך האופייני נמדד מהדופן של אורך ההתחלה הלא מחומם. ניתן גם להראות שעבור זרימה טורבולנטית:

מבחינת מספר נוסלט ממוצע, עבור זרימה למינרית או טורבולנטית:

כאשר לזרימה למינרית ו- לזרימה טורבולנטית.

פלטה שטוחה בשטף חום קבוע

קיימת גם האפשרות של שטף חום קבוע במקום טמפרטורה קבועה. במקרים אלו, עבור זרימה למינרית:

ולזרימה למינרית:

מבחינת מספר נוסלט ממוצע, ניתן להראות עבור זרימה למינרית ש:

שזה גדול רק ב- מהביטוי במשוואה (IH7.30). נקבל הבדל אפילו יותר קטן אם נחשב עבור זרימה טורבולנטית. לכן, נוכל להשתמש בכל ביטוי שפותח עבור לטמפרטורה קבועה כדי לחשב את מספר נוסלט הממוצע לשטף חום קבוע.

הסעה חיצונית על משטחים עקומים

בזרימה דיברנו על ניתוק זרימה - תופעה המתרחשת בגאומטריות לא ישרות, שזה תאכלס כמעט כל הגאומטריות.

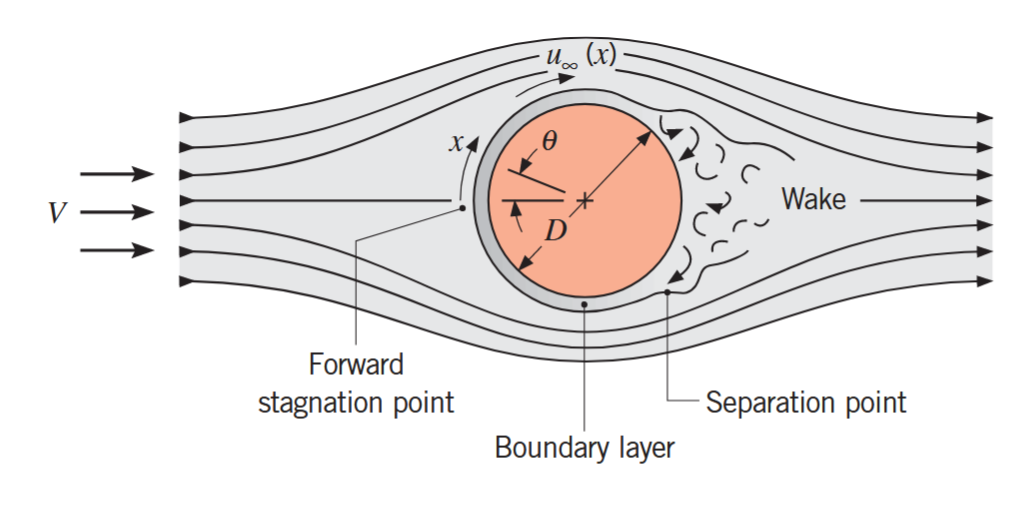
התפתחות שכבות גבול והתנתקות על גליל עגול. (Bergman & Lavine, 2017).

לאזור מאחורי הגליל באיור לעיל אנו קוראים שובל (wake).
נקודת ההתנתקות תלויה ב- :

ואנו נניח שעבור גליל, כאשר , הניתוק עוד מתרחש באזור למינרי של שכבת הגבול, וזה קורה בערך ב- . לעומת זאת, אם , אז הניתוק מתרחש באזור הטורבולנטי של שכבת הגבול, בערך ב- .

הסעה על גליל וכדור

בגרף הבא מוצגים תוצאות ניסויים למספר נוסלט לפי עבור ערכי שונים:

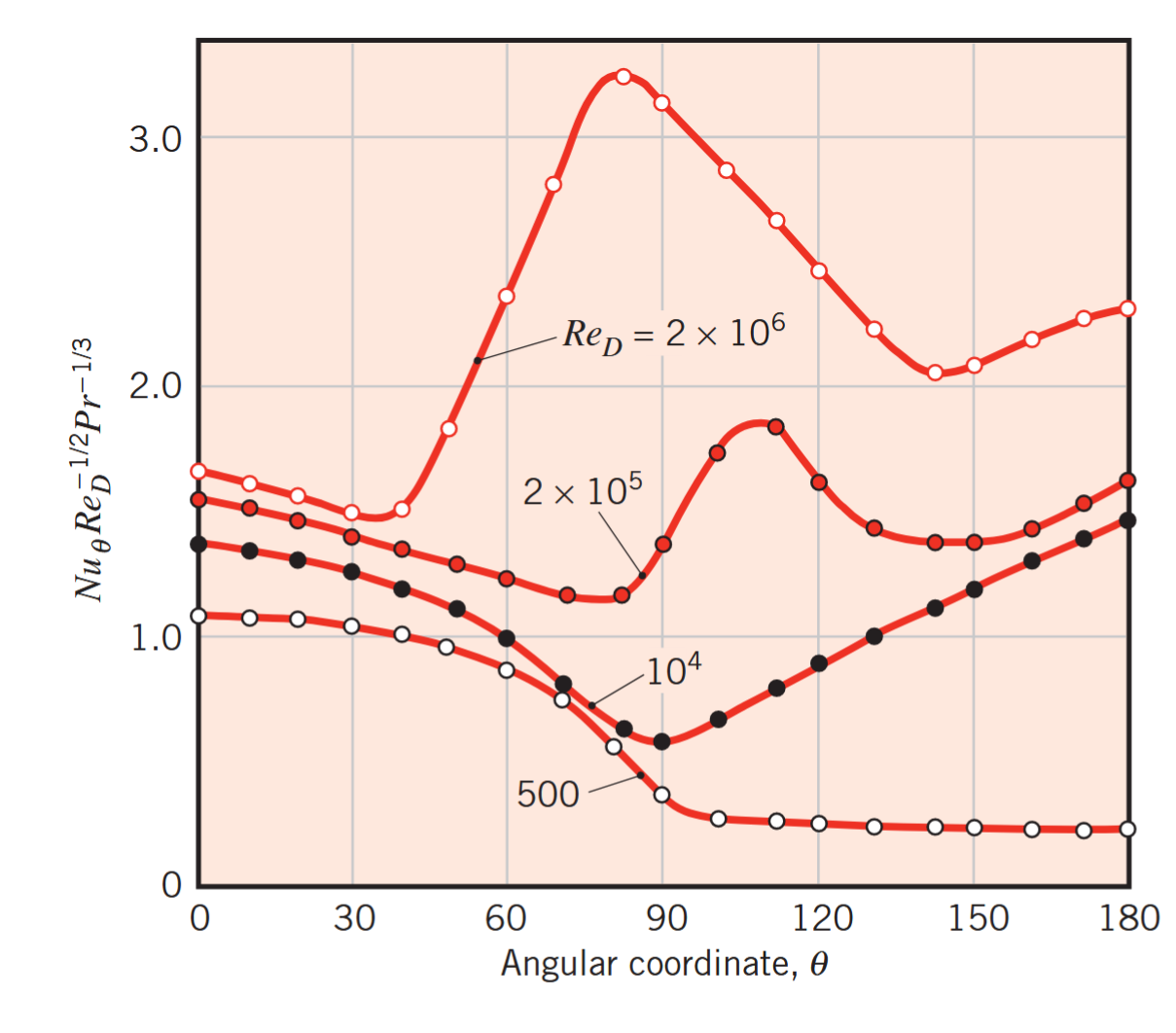
מספר נוסלט מקומי לזרימה הנורמלית לגליל עגול. (Bergman & Lavine, 2017).

לא במפתיע, תוצאות אלו משופעות מטבע התפתחות השכבות גבול על שטח הפנים של הגליל. נביט למשל בגרף של של . מנקודת הסטגנציה, קטן עם גדילת כתוצאה מגדילת שכבת הגבול הלמינרית. אבל, כאשר מגיעים למינימום ב- , מתרחש ניתוק ו- גדל עם כתוצאה מערבוב בשובל. לעומת זאת, עבור , השינוי של עם מאופיין בשתי נקודות מינימום. הירידה ב- מהערך בנקודת הסטגנציה הוא שוב, בגלל גדילת השכבת גבול הלמינרית, אבל העלייה החדש המתרחשת בין ו- היא כעת כתוצאה מהמעבר של השכבת גבול מלמינרית לטורבולנטית. עם התפתחות השכבה הטורבולנטית, שוב מתחיל לרדת. לבסוף הוא מגיע לניתוק () ו- גדל כתוצאה מערבוב באזור השובל.

לא ניתן לקבל פתרון אנליטי עבור גלילים במספר לא למינרי לחלוטין. לכן, מוצאים התאמה אמפירית לניסוי - מחפשים קורלציה. מצאו כי:

כאשר , והקבועים ו- תלויים ב-, וערכיהם נתונים בטבלה 7.2.
ישנה עוד קורלציה שמכילה את כלל טווחי ה- עבורם קיים מידע אימפירי, והיא גם נכונה לטווח מאוד רחב של ערכי . מומלץ להשתמש בה לכל , ויש לה את הצורה:

כאשר כל הערכים מחושבים בטמפרטורה הממוצעת ( עבור film):

עבור כדור:

כאשר ו- הם הצמיגות ב- והצמיגות בשפת הכדור בהתאמה. כל הערכים חוץ מ- מחושבים ב-.

זרימה לאורך מערך גלילים

מעבר חום ממערך גלילים בזרימה מציפה רלוונטי למספר יישומים תעשייתיים, כמו יצירת קיטור בדוד או קירור בצינורות של מזגן. גאומטריית מערך גלילים טיפוסית היא מהצורה:

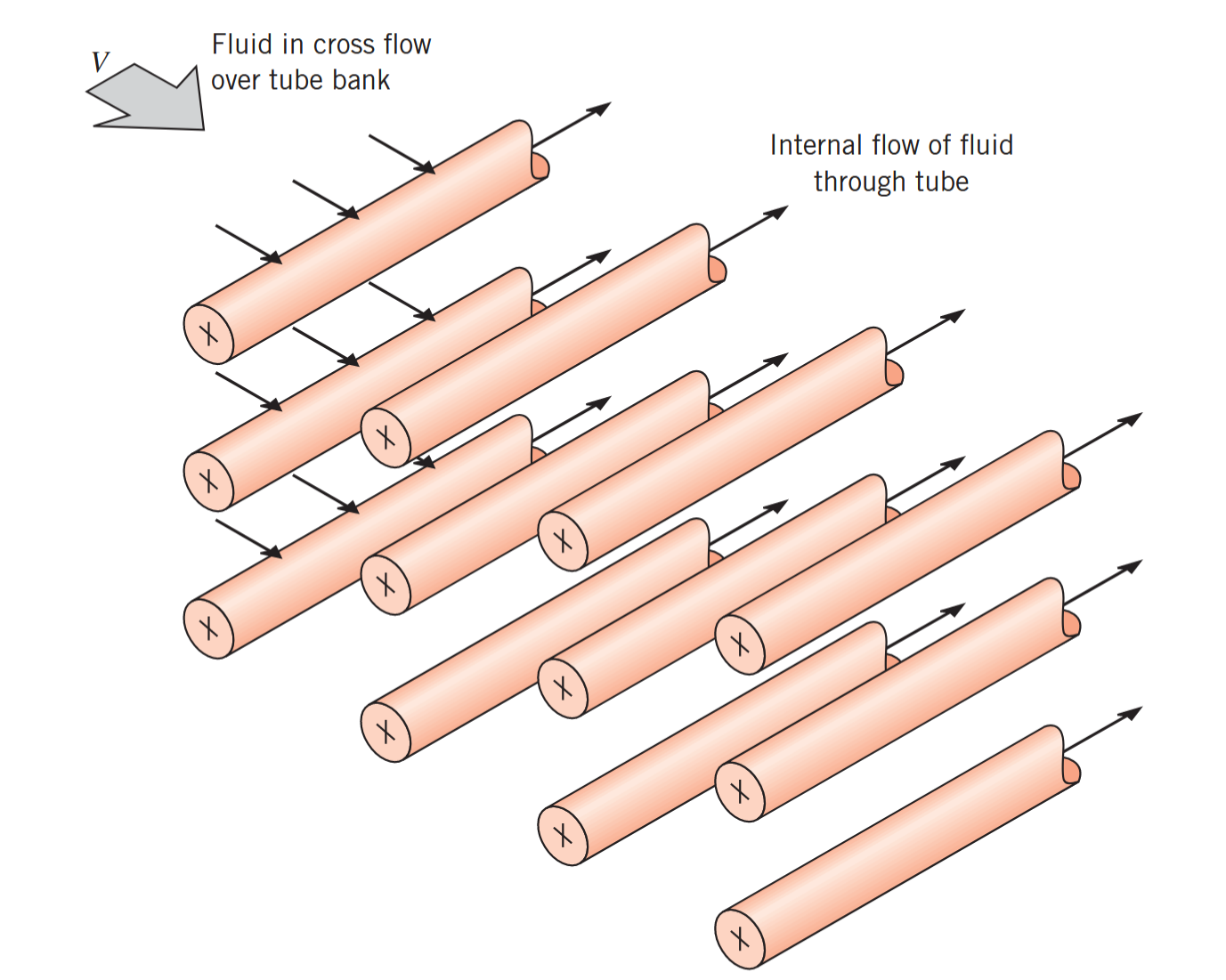
סכמה של צינורות בזרימה מציפה. (Bergman & Lavine, 2017).

בדרך כלל, זורם אחד עובר על הצינורות, בעוד זורם שוני בטמפרטורה שונה זורם דרך הצינורות. בפרק זה אנו דנים ספציפית בהסעה של הזרימה המציפה על הצינורות.

המערך גלילים יכול להיות מסודר או בצורה ישרה (aligned) או מדורגת (staggered) לכיוון הזרימה שבמהירות .

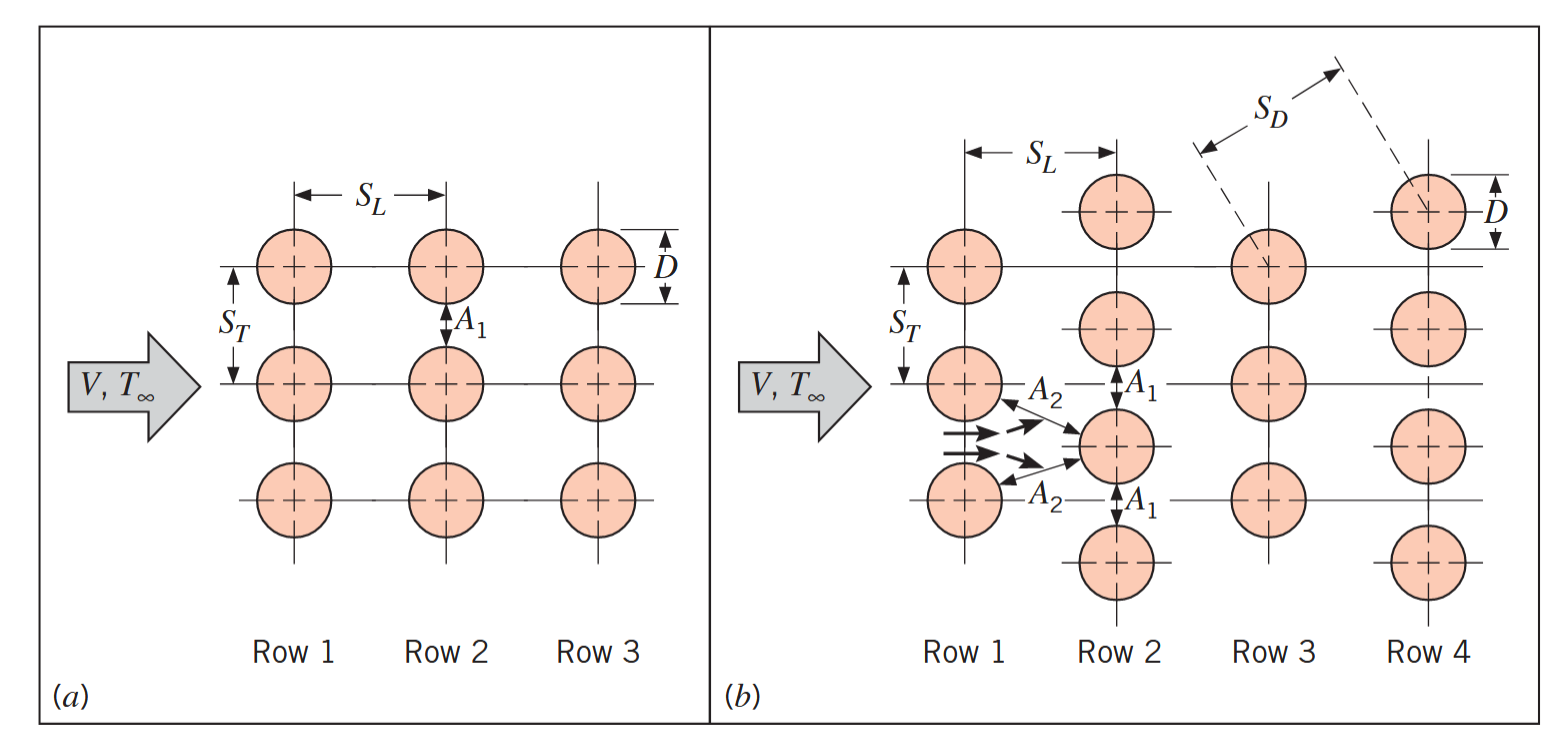
אופן סידור מערך הגלילים. (a) מיושר. (b) מדורג. (Bergman & Lavine, 2017).

התצורה מאופיינת ע”י קוטר גליל , פסיעה רוחבית (transverse pitch) ופסיעה אורכית (longitudinal pitch) הנמדדת בין מרכזי גלילים. תנאי הזרימה בתוך המערך נשלטים בעיקר ע”י שכבות גבול, ניתוקים, ואינטראקציות השובלים, שכולם משפיעים על מעבר החום בהסעה.

זרימה סביב הגלילים בשורה הראשונה של המערך דומה לזו סביב גליל אחד. לכן, מקדם מעבר החום עבור המערך בשורה הראשונה הוא בערך שווה למקדם עבור גליל אחד. עבור השורות הבאות, זה כבר תלוי באופן הסידור של מערך הגלילים.

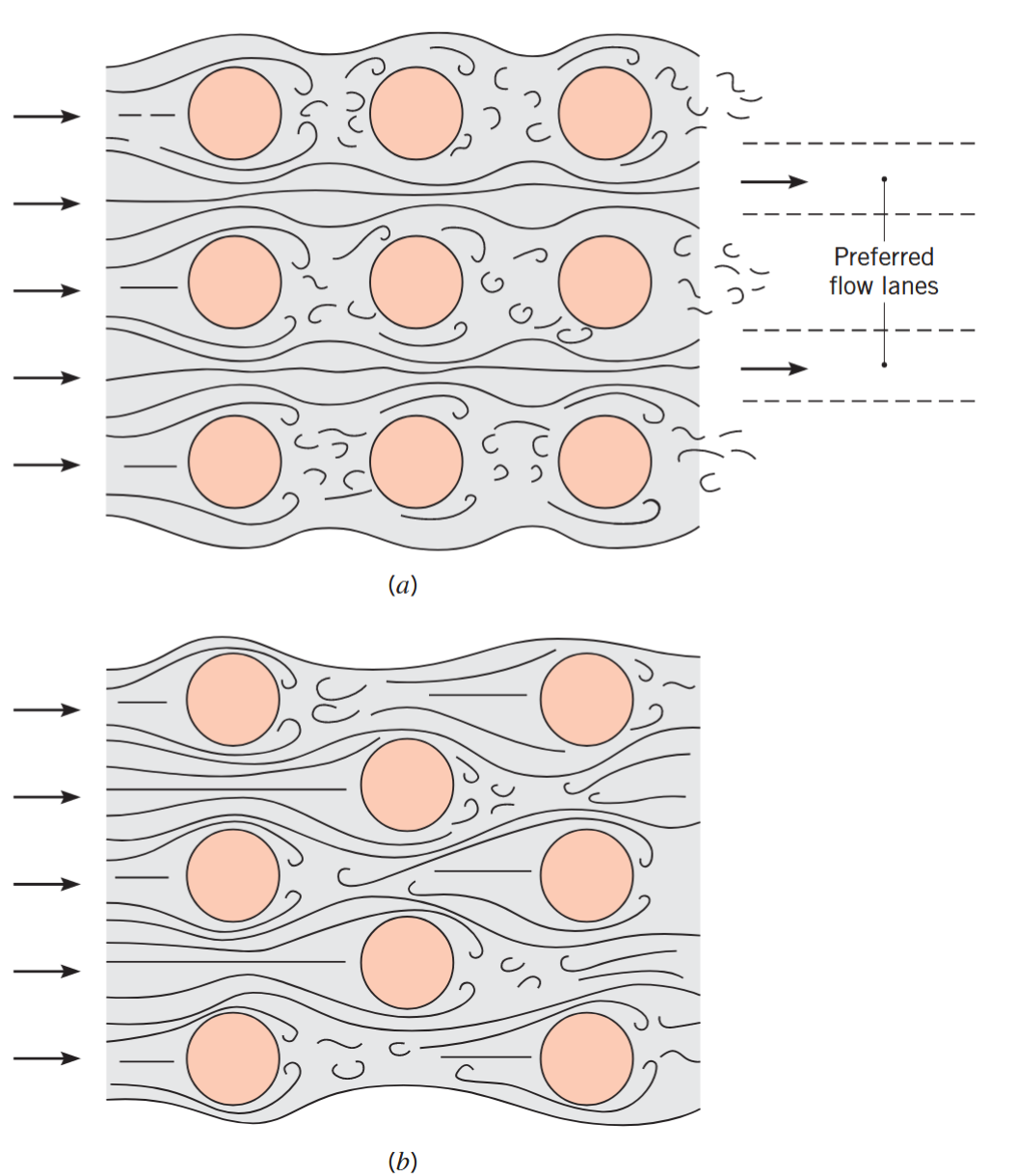
תנאי זרימה עבור (a) סידור ישר ו-(b) סידור מדורג. (Bergman & Lavine, 2017).

גלילים מיושרים מעבר לשורה הראשונה נמצאים בשובלים של הגלילים במעלה הזרימה, ועבור ערכי בינוניים, מקדמי ההסעה המתאימים לשורות במורד הזרימה משופרים כתוצאה מהערבוב, או הטורבולנציה, של הזרימה. בדרך כלל, מקדם ההסעה של שורה גדל ככל שמספר השורה גדל עד בערך השורה החמישית, אחריה ישנו שינוי קטן. עבור ערכי גדולים, ההשפעה של הגלילים במעלה הזרימה קטנים, כך שמקדמי ההסעה לא משופרים, ולכן לא מומלץ לעבור עם מערכי גלילים מיושרים בהם .
עבור גלילים מדורגים, מסלול הזרימה יותר כאוטי, וערבוב הזרימה גדל ביחס למערך הגלילים המיושר. בכללי, מעבר החום יותר טוב עבור הזרימה היותר כאוטית של מערך מדורג, בייחוד עבור ערכי ריינולדס קטנים ().
לרוב, נרצה לדעת את מקדם מעבר החום ה-ממוצע של כלל מערך הגלילים. מניסויים, נמצא הקשר הבא:

כאשר הוא מספר השורות במערך, וכלל הערכים חוץ מ- מחושבים עבור טמפרטורות הכניסה () וטמפרטורות היציאה (). בנוסף, ערכי ו- מפורטים בטבלה 7.5. מחושב עבור טמפרטורת שפת הגלילים. את נראה איך מחשבים בהמשך.

אם יש או פחות שורות של צינורות, , מקדם מעבר החום צריך להיות מוקטן במקדם תיקון :

כאשר נתון בטבלה 7.6.

מספר ריינולדס המקסימלי מבוסס על הנקודה בה מהירות הזורם היא מקסימלית:

למערך ישר, מתרחש ב- באיור השני בזרימה לאורך מערך גלילים, ומשימור מסה ניתן להראות ש:

למערך מדורג, המהירות המקסימלית מתרחשת או ב- או ב-. היא ב- אם:

לכן, מתרחש ב- אם:

ואז:

אם מתרחש ב- למערך מדורג, נוכל לחשב אותו פשוט ע”י (IH7.60)

מאחר והזורם יכול לחוות שינוי גדול בטמפרטורה כאשר הוא נע דרך מערך הצינורות, קצב מעבר החום כבר לא פרופורציונלי ישירות ל- . כאשר הזורם נע דרך המערך, הטמפרטורה שלו מתקרבת ל- ו- קטן. ניתן להראות שהצורה המתאימה של היא מה שנקרא ממוצע לוגריתמי , שניעזר בו במחליפי חום:

כאשר ו- הם טמפרטורות הזורם כאשר הוא נכנס ויוצא מהמערך, בהתאמה. הטמפרטורה ביציאה, שצריך אותה כדי לחשב את , ניתנת לחישוב מ-(נובע מחוק ראשון):

כאשר הוא מספר הצינורות במערך ו- הוא מספר הצינורות בכל שורה. ברגע ש- ידוע, קצב מעבר החום ליחידת אורך של הצינור ניתן לחישוב מ:

תרגילים

תרגיל 1

נתונים ביטויים למקדמי מעבר חום בהסעה מקומיים עבור זרימה מקבילה ללוח ישר, גם למינרית וגם טורבולנטית:

סעיף א’

מהו מקדם מעבר החום הממוצע בהסעה על גבי פלטה באורך בכיוון הזרימה?

פתרון:
לפי זרימה מעורבת:

נחשב כל אינטגרל בנפרד:

נקבל:

סעיף ב’

האם קיים אורך עבורו מקדם מעבר החום הממוצע בהסעה זהה עבור זרימה למינרית ועבור טורבולנטית? אם כן, מהו?

פתרון:
נמצא מתי :

נציב נתונים ונקבל:

תרגיל 2

כדי למנוע היווצרות קרח על כנפי מטוס, מוצע להתקין גופי חימום על הכנפיים. האורך האופייני של חתך הכנף הוא . בניסוי מנהרת רוח נמדד חיכוך ממוצע . מהו שטף החימום הממוצע הדרוש לשמירת טמפרטורת הכנף . במצב טיסה סטנדרטי בו המטוס טס במהירות באוויר בטמפרטורה ?
תכונות האוויר:

פתרון:
שטף החום הממוצע הדרוש הוא:

בהזנחת גרדיאנט לחץ בסביבת המטוס, ניתן להעריך את מקדם מעבר החום בהסעה באמצעות אנלוגיית ריינולדס:

נחלץ את מקדם מעבר החום הממוצע בהסעה:

נשים לב כי:

ולכן:

מה שאומר שמקדם מעבר החום הממוצע:

ומכאן:

שאלה 3

אוויר בלחץ אטמוספרי וטמפרטורה זורם מעל לוח ריבועי . מהירות האוויר רחוק מהלוח היא . הלוח מצוי בטמפרטורה אחידה של .

סעיף א’

מצאו את עובי שכבת הגבול התרמית בקצה הלוח.

פתרון:
ראשית, נמצא את תכונות האוויר:. עבור הטמפרטורה הממוצעת:

התכונות הן:

נמצא אם אנחנו בתחום טורבולנטי או למינרי:

לפי פתרון בלסיוס, עבור האזור הלמינרי, משוואה (IH7.19):

ולכן בקצה הלוח:

את עובי שכבת הגבול התרמית נמצא בעזרת משוואה (IH7.24):

נציב ערכים ונקבל:

סעיף ב’

מהו שטף החום הממוצע על פני הלוח?

פתרון:
לפי הגדרת שטף החום:

את מספר נוסלט נמצא ממשוואה (IH7.30):

ולכן שטף החום:

סעיף ג’

בניסוי נמדד על הלוח כוח הגרר . תוך שימוש בנתון זה ובאנלוגיית ריינולדס חזרו על סעיף ב’.

פתרון:
מתוך הגדרת כוח הגרר ומקדם החיכוך:

מנגד, מאנלוגיית ריינולדס, משוואה (IH6.70):

נשווה בין שני הביטויים ל- שקיבלנו:

לכן שטף החום:

נציב ערכים ונקבל:

שאלה 4

משטח של גוף חימום מוחזק בטמפרטורה של . המשטח מחולק לשתי פרוסות: אחת חלקה והשנייה מחוספסת מאוד. המשטח חשוף לזרימת אוויר בטמפרטורה ומהירות . הפרוסה המחוספסת בעלת פני שטח גס מאוד כך שהזרימה מעליה בתנאים הנ”ל טורבולנטית.

סכמת המשטחים

סעיף א’

חשבו את קצב מעבר החום הכולל ליחידת רוחב מן המשטח כאשר הפרוסה המחוספסת ממוקמת ב-מעלה הזרם.

פתרון:
תכונות האוויר עבור :

לפי זרימה מעורבת, משוואה (IH7.38):

מאחר והזרימה תהיה טורבולנטית מההתחלה, מהגדרת במשוואה (IH7.39) נקבל ש- , ואז:

ולכן קצב המעבר חום ליחידת רוחב:

נקבל:

סעיף ב’

חשבו את קצב מעבר החום הכולל ליחידת רוחב מן המשטח כאשר הפרוסה המחוספסת ממוקמת ב-מורד הזרם.

פתרון:
באותו אופן כמו סעיף קודם, רק הפעם נשים לב שאנחנו מתחילים מזרימה למינרית, ועלינו לבדוק אם אנו בכלל מגיעים לזרימה טורבולנטית:

קיבלנו ש- ולכן יכול להיות שהזרימה משתנה מלמינרית לטורבולנטית איפשהו על הפלטה החלקה. נבדוק איפה נקודה קריטית זו:

כלומר, קיבלנו שהזרימה משתנה לטורבולנטית איפשהו באמצע, לפני המעבר למשטח המחוספס. משוואה (IH7.38) עדיין תקפה, אבל הפעם:

נציב ונקבל:

ולכן קצב המעבר חום:

סעיף ג’

חזרו על הסעיף הקודם אבל עבור זרימת אוויר במהירות .

פתרון:
נבדוק שוב אם עד חצי מהאורך הכולל (כלומר, בפלטה החלקה) יש מעבר לזרימה טורבולנטית:

נסיק שעד מחצית מהאורך הכולל אין מעבר לזרימה טורבולנטית. אבל, מאחר ואנו עוברים לפלטה המחוספסת, נעבור בכל זאת לאזור טורבולנטי ב-, מה שאומר שאנו כבר לא עובדים עם ה- הרגיל של המערכת, ואנו צריכים לחשב את ערך , כדי לקבל את :

לפי משוואה (IH7.39):

שוב, לפי משוואה (IH7.38):

לכן מקדם מעבר החום הוא:

→ קודם: HTF1_004הבא: HTF1_006 ←