FLD1_E2021WA 2021 חורף מועד א'

שאלה 1

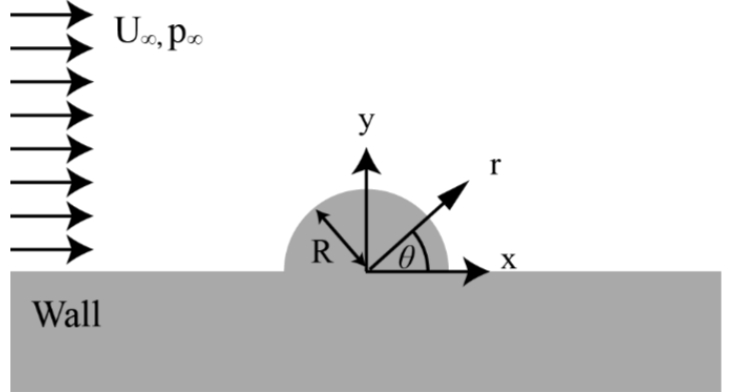
סכמת הבעיה

סעיף א’

עבור זרימה פוטנציאלית נדרוש ש- , וגם אי-רוטוציוניות - .

סעיף ב’

לפי זרימה סביב גליל, נמדל את הבעיה כסופרפוזיציה של זוגן וזרימה מציפה:

לכן המהירות בכיוון :

נדרוש אי-חדירה ב-:

נציב בחזרה ב-:

ולכן שדה המהירות:

ספציפית, על הגליל (ב- ):

סעיף ג’

כיוון שאנו בזרימה פוטנציאלית, נוכל להשתמש במשוואת ברנולי. נבחר נקודה רחוקה ב- רחוקה מספיק כך שהמהירות בה היא פשוט המהירות המציפה והלחץ , ועוד נקודה על שפת הגליל:

סעיף ד’

נסכום את הלחצים על חצי מהגליל כדי לקבל את סך הכוח שפועל עליו:

נפרק לשתי הכיוונים. בכיוון :

בכיוון :

ולכן הכוח:

שאלה 2

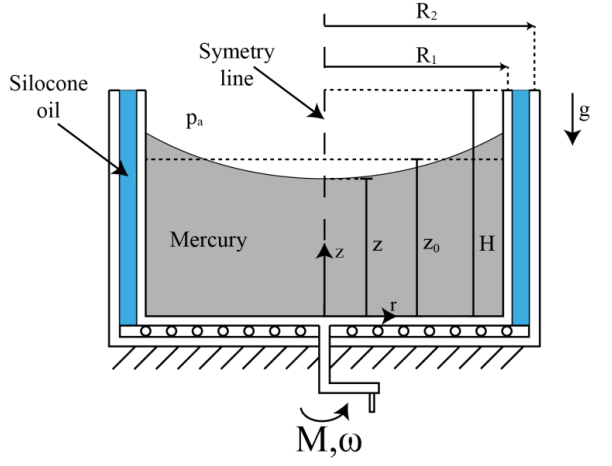
סכימת הגלילים

סעיף א’

במצב מתמיד הזורם כבר הפסיק לזוז, ופועל עליו רק הכוחות גוף - כוח הכבידה והכוח הצנטריפוגלי (במערכת צירים המסתובבת עם הגליל). לכן, נסיק כי אנו במשטר הגבול ההידרוסטטי.

סעיף ב’

בהידרוסטטיקה לא אינרציאלית, המשוואות הן:

במקרה שלנו, וגם (כוח צנטריפוגלי במערכת צירים מסתובבת - לא אינרציאלית). לכן, אם נפרק לכיוונים:

מאחר והבעיה אקסיסימטרית, נוכל לומר כי , כך ש- . נבצע אינטגרציה על כיוון :

נגזור לפי :

נשווה ל- שקיבלנו ממשוואות ההידרוסטטיקה:

נציב בחזרה ב-:

אנו יודעים שב- ו- הלחץ הוא אטמוספירי:

נציב בחזרה:

כדי למצוא את פרופיל פני השטח של הזורם , נציב , כי אנו יודעים שבפני השטח של הזורם הלחץ הוא אטמוספירי:

כעת נרצה למצוא את העקמומיות לפי הנוסחה שנתונה. נשים לב כי:

ב- :

נציב בנוסחה לעקמומיות:

לכן, כדי לקבל את עקמומיות זו, על לקיים:

חוסר הרלוונטיות של החלק האחרון של השאלה הזאת מרגיש כאילו עשו פה מהלך תהליכי ייצור.

סעיף ג’

מערכת הצירים הפולארית. מאחר ואנו מזניחים כבידה, הזרימה דו-ממדית.

נניח כי:

1. הגאומטרייה תמירה (ממד ארוך ביחס לממד ).
2. הבעיה אקסיסימטרית - .
3. מצב מתמיד - .
4. הזרימה דו-ממדית - , .
5. כבידה זניחה.

נביט במשוואת הרצף:

ולכן בכיוון :

נביט במשוואות נאוויה-סטוקס בכיוון :

נישאר עם:

לגבי תנאי שפה על , אנו יודעים שהגליל החיצוני לא מסתובב, והגליל הפנימי מסתובב במהירות זוויתית . לכן, מאי-החלקה:

מאי חדירה, אנו יודעים כי:

סעיף ד’

בסעיף קודם מצאנו כי , אבל גם שתנאי השפה שלו בקצוות הם אפסיים, כך שלמעשה:

נציב בחזרה במשוואה שקיבלנו עבור :

נציב את התנאי שפה שמצאנו על :

נציב את בחזרה בביטוי שמצאנו ל-:

נציב בחזרה ב-:

או, כמו שרשום בתשובות הסופיות:

סעיף ה’

מטנזור מאמץ לנוזל ניוטוני, אנו יודעים שמאמץ הגזירה בקואורדינטות פולאריות נתון ע”י:

נציב את שמצאנו (לפני שהצבנו את המקדמים, לפישוט):

נרצה למצוא את ספציפית ב- :

נסכום את המומנט שמאמץ גזירה זה יותר סביב מרכז הגליל, לאורך כל היקף הגליל:

נציב את שמצאנו ונסיק כי:

כדי לקבל את העקמומיות הדרושה, נדרוש :

שאלה 3

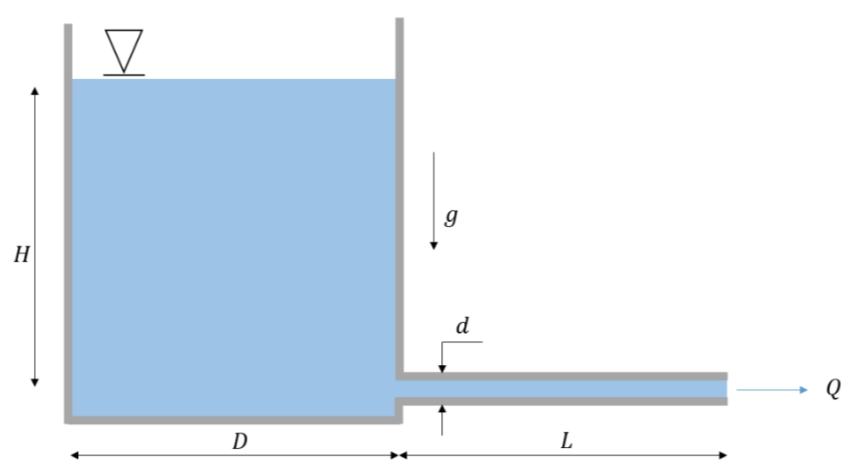
סכימת המיכל

סעיף א’

לפי הגדרות מספרי פראוד וריינולדס:

האורך האופייני במיכל הוא (מהנתונים). כדי למצוא את המהירות האופיינית במיכל , נמצא את המהירות האופיינית שבצינור ונקשר בעזרת שימור מסה. נניח שפרופיל מהירות היציאה מהצינור הוא אחיד, כך ש:

לפי שימור מסה אינטגרלי זריז על המיכל:

נציב בחזרה בפראוד וריינולדס:

סעיף ב’

בהנחת גופים דקים נוכל להשתמש בריינולדס מוקטן:

מבחינת הממד הארוך (), אין כוחות גוף, כך שמספר פראוד הרלוונטי הוא פשוט אפס.

סעיף ג’

עבור המיכל, אנו במשטר הידרוסטטי (מתקיים וגם ), ולכן המשוואות הן:

במקרה שלנו, תחת כבידה:

מאחר ואנו יודעים ש- , נסיק כי:

עבור הצינור, הגאומטרייה תמירה ומתקיים . לכן, נניח כי:

1. המצב תמידי - .
2. הזרימה מפותחת - .
3. הבעיה אקסיסימטרית - .
4. כבידה זניחה.

לפי משוואת הרצף:

מאי-חדירה, אנו יודעים ש- , ולכן, טענה מספר :
5. המהירות הרדיאלית אפסית - .

לפי משוואות נאוויה-סטוקס בכיוון (כאשר הוא הכיוון הארוך):

נישאר עם:

סעיף ד’

נפתח למעשה את זרימת הייגן-פואזיי. מהמשוואה שקיבלנו סעיף קודם, צד שמאל תלוי רק ב-, ואילו צד ימין תלוי רק ב-, כך שנוכל להסיק כי:

נשים לב שכאשר , הביטוי שואף ל-, מה שאנו יודעים שפיזיקלית לא נכון. לכן , ונישאר עם:

מאי-החלקה, אנו יודעים ש- , ולכן:

נציב בחזרה בפרופיל המהירות ונסיק כי:

אנו גם יודעים ש:

בהתחלה (), הלחץ הוא (מהמשוואה שמצאנו עבור לחץ המיכל), ובסוף , הלחץ הוא אטמוספירי. נציב את תנאי שפה אילו ונסיק כי:

ולכן . נציב בחזרה ב-:

שאלה 4

סעיף א’

המאזניים ייטו לצד הכדור הכחול - כלומר, בצד ימין יופעל יותר כוח על המאזניים. הסיבה לכך היא שבשני המיכלים, על הכדורים פועל כוח ציפה זהה כלפי מעלה, כך שלפי חוק שלישי של ניוטון פועל על המים כוח זהה כלפי מטה. אבל, במיכל השמאלי, כוח זה מבוטל ע”י המיתר שמפעיל כוח כמעט זהה כלפי מעלה. לכן, בסה”כ, על המיכל הימני מופעל יותר כוח כלפי מטה.

סעיף ב’

נרצה למצוא את הכוחות על כל אחד מהכדורים:

דג”ח על כל אחד מהכדורים. כוח הציפה זהה בשניהם כי הם מזיזים את אותו נפח המים (ארכימדס).

שני הכדורים בשיווי משקל, כך ש:

כוח הציפה, לפי ארכימדס, הוא כאשר הוא נפח הכדור. בנוסף, מאחר והמסות אחידות, נוכל לחשב אותן כמכפלה של הצפיפות והנפח שלהן. לכן:

נרצה כעת לחשב את הכוח שהמיכלים מפעיל על המאזניים, .

דג”ח על שני המיכלים. נשים לב שעל הנוזל פועל כוח הציפה בכיוון ההפוך, לפי חוק שלישי של ניוטון.

מאחר ואנו בשיווי משקל, סך הכוחות על כל מיכל אפסי, כך ש:

נסיק כי , כך שהמאזניים ייטו לצד ימין.