FLD1_HW004 תרגיל בית 4

	סטודנט א’
שם	עידו פנג בנטוב
ת”ז	CLASSIFIED
דואר אלקטרוני	CLASSIFIED

שאלה 1

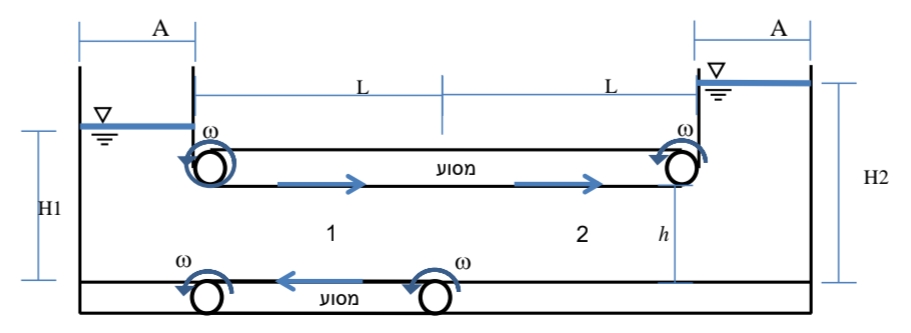
סכימת התעלה

סעיף א’

נבחר מערכת צירים קבועה בתחתית המסועה, בתחילתה:

בחירת מערכת צירים בתחתית המסועה

מהנתונים נניח את ההנחות הבאות:

1. כיוון ש- , נוכל להניח כי הגאומטרייה תמירה
2. השפעות הכבידה בתעלה זניחות (כי הגאומטרייה תמירה)
3. הבעיה דו-ממדית
4. מהירות שינוי גובה המיכלים קטנה משמעותית ממהירות הזורם בתעלה, כך שניתן לומר כי המצב מתמיד -
5. הזרימה מפותחת - .

ממשוואת הרצף:

סימון הביטול ל- מעיד על ההנחה שלפיה ביצענו את הביטול.
נניח גם את תנאי האי-חדירה ואי-החלקה (הזרימה צמיגה), כך ש:

ולכן:

6. אין מהירות בכיוון האנכי - .

לפי משוואות נאוויה-סטוקס הדו-ממדיות, בכיוון :

בנוסף, אין כוחות גוף בכיוון . נישאר עם:

לפי משוואות נאוויה-סטוקס הדו-ממדיות, בכיוון :

נישאר עם:

עבור שאר תנאי השפה, נתון כי אנו יכולים להניח פילוג לחץ הידרוסטטי במכלים. אבל, נשים לב כי , וגם כי . לכן, נניח שבקצוות ישנו לחץ אחיד לאורך , שגודלו נקבע לפי משוואות ההידרוסטטיקה (במקרה שבו מופעל רק כוח הכבידה):

במקרים שלנו, עבור ההתחלה והסוף ישנם שני קבועים שונים:

ולכן בתחתית התעלה:

תנאי ההתחלה שלנו:

• במחצית הראשונה של התעלה:
• במחצית השנייה של התעלה:

סעיף ב’

את המהירויות בקצוות קל לשרטט מאחר והם פשוט תנאי השפה (מסעיף קודם).
מבחינת שאר הגבהים, נוכל להסיק מסופרפוזיציה של זרימת קואט וזרימת פואזיי (פרבולי):

פרופילי המהירות בשני האזורים

סעיף ג’

מסעיף א’, קיבלנו את המד”ח:

מאחר ו- לא תלוי ב- (הרי מתקיים ), נוכל לבצע אינטגרציה פשוטה, פעמיים:

מהעברת אגפים:

את ו- נוכל למצוא מתנאי שפה על המהירות, עבור כל אחד מהאזורים בנפרד, שנבצע בהמשך. נתמקד בביטוי .
אם נביט במשוואה , כיוון שהראינו ש- לא תלוי ב- (טענה ) אז גם בהכרח לא תלוי ב-. מאחר וגם לא תלוי ב-, נקבל כי:

נמשיך באינטגרציה על :

נגדיר את הלחץ בין שני האזורים כ-.

• עבור אזור , התנאי שפה על הלחצים: ולכן, באזור : נציב גם את התנאי שפה על המהירויות: לכן, באזור : נציב את : כאשר את נמצא בהמשך.

עבור אזור , (נזיז את ראשית הצירים לתחילת אזור ) התנאי שפה על הלחצים:

ולכן, באזור :

נציב גם את התנאי שפה על המהירויות:

לכן, באזור :

נציב את :

נותר למצוא מהו . מחוק שימור המסה האינטגרלי (נפח בקרה קבוע על היציאה והכניסה):

בחזרה ב-:

נקבל ש:

ובאותו אופן עבור אזור :

סעיף ד’

אנו נגיע למצב מתמיד כאשר הספיקה דרך אחד מהאזורים הוא (ואז גם בהכרח הספיקה מהאזור השני תהיה ). נבחר ב-. אזי, נדרוש ש:

בהתחלה בכל מיכל הגובה הוא , ולכן בסוף (משימור נפח), נסיק כי:

משתי משוואות אלו נקבל:

שאלה 2

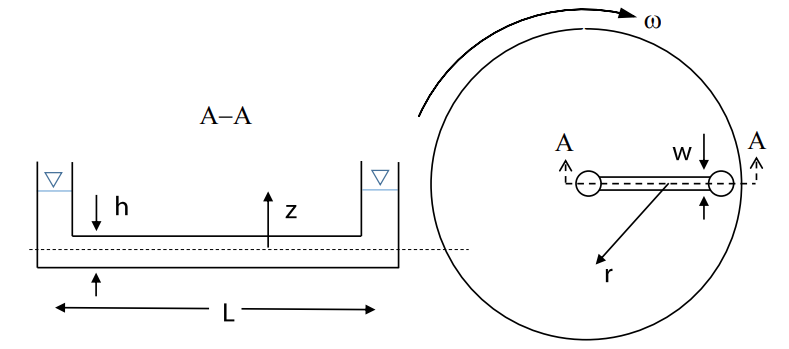
סעיף א’

נבחר את מערכת הצירים:

נניח את ההנחות הבאות:

1. האינרציה זניחה
2. גאומטרייה תמירה ()
3. כבידה זניחה (עדיין יש כוחות גוף, הכבידה זניחה ביחס אליהם)
4. בעיה דו ממדית
5. הזרימה מפותחת - .

לפי משוואת הרצף במקרה הדו-ממדי (עם ו-):

נסיק כי:

נוסיף ונאמר שמתקיים אי-חדירה, כך ש- . לכן, טענה :

6. מתקיים .

ממשוואות נאוויה-סטוקס בכיוון :

נישאר עם:

כוחות הגוף הם הכוחות הצנטריפוגליים (מערכת צירים לא אינרציאלית) - . לכן:

כדי לקבל את המשוואה המנורמלת, ננרמל לפי גדלים אופייניים:

נציב במשוואה שקיבלנו:

אנו נרמלנו את הגדלים במשוואה, כך ש- הם כולם מאותו הסדר גודל .
כדי לקבל את הגדלים האופייניים, נדרוש שכל המקדמים של הגדלים החסרי-ממד באותו סדר הגודל (כמו שהוסבר ב[[FLD1_006 צמיגות#שאלה 3#סעיף א’|שאלה בתרגול]]):

נקבל את הגדלים האופייניים:

נציב אותם בחזרה במשוואה ונקבל כי:

ממשוואות נאוויה-סטוקס בכיוון :

ולכן, המשוואה הלא מנורמלת:

סעיף ב’

כדי שהאינרציה תהיה זניחה, נדרוש שמספר ריינולדס המוקטן יקיים :

נציב את המהירות האופיינית מסעיף קודם (שמתקבל אם האינרציה זניחה):

סעיף ג’

מהמשוואה המנורמלת מ[[#שאלה 2#סעיף א’|סעיף א’]], נסיק כי המשוואה הלא מנורמלת היא:

כאשר הגדלים מופיעים בחזרה כי הם גדלים שלא נרמלנו.
אנו גם יודעים ש- , כלומר אגף שמאל הוא פונקציה אך ורק של . עבור אגף ימין, מאחר והזרימה מפותחת (), אנו יודעים שהוא פונקציה אך ורק של .
לפיכך, מאחר והם שווים, נסיק כי השוויון לעיל שווה לקבוע:

לפיכך:

נניח הידרוסטטיקה בשני המיכלים, כאשר גובה המיכל במרכז הוא , וגובה המיכל הקיצוני הוא (ההנחה שהגבהים לא בהכרח שווים תעזור לנו בסעיף ה’). לכן, הלחץ בתחתית הבאריות:

ולכן:

נחזור למשוואה:

נציב את שמצאנו:

נעביר אגפים ונחלק ב-:

נסמן את אגף ימין ב- (כי זה גודל קבוע). נבצע אינטגרציה פעמיים:

נניח תנאי-אי החלקה, כך שבעצם תנאי השפה שלנו הם:

ולכן:

נציב בחזרה את :

כאשר גובה המים זהה, יתקיים:

אם מערכת הצירים שלנו הייתה ממוקמת באמצע הגובה של הצינור, היינו מקבלים את הפתרון הרשמי:

סעיף ד’

פרופילי המהירות בחתכים שונים

הראנו כבר שהזרימה מפותחת, כך שפרופיל המהירות זהה בכל החתכים.

סעיף ה’

נגיע למצב מתמיד כאשר הספיקה בתעלה תתאפס. כלומר, כאשר:

כאשר לא משנה באיזה חתך נבחר לחשב את . נציב את הכללי מ[[#שאלה 2#סעיף ג’]]:

לכן הפרש הגבהים יהיה:

שאלה 3

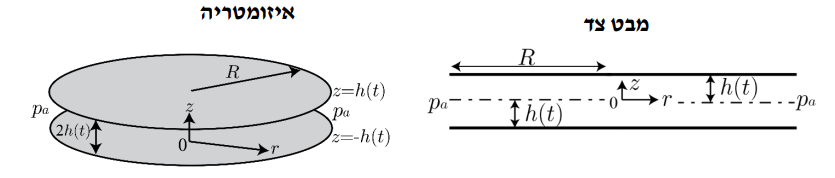
סכימת הפלטות

סעיף א’

נניח את ההנחות הבאות:

1. כוחות גוף מוזנחים -
2. הבעיה אקסיסימטרית -
3. הלחץ תלוי רק בכיוון -
4. המהירות בציר תלויה רק בכיוון -

לפי משוואת הרצף:

ננרמל לפי:

נציב ונקבל:

הגדלים המנורמלים בסדר גודל , כך שנוכל להשוות בין המקדמים שלהם:

נציב נתונים התחלתיים ונקבל:

סעיף ב’

האינרציה זניחה אם . נשים לב ש- , כך שנוכל אפילו להסתפק בתנאי על ריינולדס המוקטן, . כלומר:

נציב נתונים ונמצא כי אכן:

לפיכך, טענה מספר :

5. אינרציה זניחה

סעיף ג’

נבחר את נפח הבקרה הבא:

בחירת נפח בקרה שמשתנה בזמן - הגבול העליון והתחתון צמוד לפלטות שמתקרבות אחת לשנייה.

לפי שימור מסה אינטגרלי:

הצפיפות אחידה ולכן נוכל לחלק אותה:

הנפח של נפח הבקרה הוא פשוט:

שטח הפנים דרכו יוצאים המים הוא:

נרצה למצוא את המהירות הממוצעת, שהיא שווה למקרה בו המהירות אחידה לאורך היציאה. נציב:

סעיף ד’

המהירות הממוצעת נתונה ע”י:

נציב את שקיבלנו בסעיף קודם:

לפי הגדרת , נסיק כי:

נציב:

הפלטות קשיחות, ונשארות מקבילות לאורך כל התהליך, כך ש- תלוי אך ורק ב-. לכן, נוכל לטעון כי:

סעיף ה’

ניעזר בכל ההנחות והטענות שרשמנו בסעיפים קודמים.
לפי משוואות נאוויה-סטוקס בכיוון :

נישאר עם:

ב[[#שאלה 3#סעיף א’|סעיף א’]] ראינו כי ממשוואת הרצף:

מאחר ו- הוא פונקציה של בלבד (הנחה ), נסיק כי כאשר נגזור אותו לפי , הביטוי ייתאפס. נישאר עם:

באותו אופן, נקבל בכיוון ש:

נישאר עם:

מבחינת תנאי שפה, אנו יודעים כי בסביבה ישנו לחץ אטמוספירי:

מתנאי אי-החלקה, המהירות הרדיאלית סמוך לפלטות היא אפסית:

סעיף ו’

אנו יודעים כי:

ראינו גם ש- , ולכן:

אנו גם יודעים ש- , כלומר אגף שמאל הוא פונקציה אך ורק של . עבור אגף ימין, אנו יודעים שהוא פונקציה אך ורק של . לכן, נוכל לומר כי:

נביט באגף ימין:

נבצע אינטגרציה פעמיים לפי :

מתנאי השפה על , נוכל להסיק שתנאי השפה על הם:

לכן:

אנו גם יודעים (מ[[#שאלה 3#סעיף ד’|סעיף ד’]])ש:

נציב את :

נחזור ל-:

נציב את שקיבלנו:

נבצע אינטגרציה:

מתנאי שפה אנו יודעים כי:

נציב ונקבל:

שאלה 4

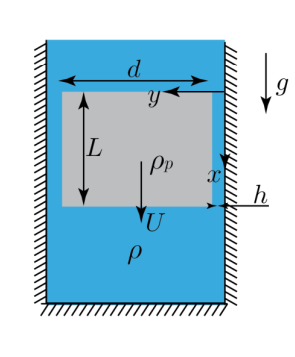
סכימת הבוכנה

סעיף א’

נניח את ההנחות הבאות:

1. הזרימה צמיגה
2. הבעיה דו-ממדית
3. במרווח בין דפנות הבוכנה לדפנות המיכל, הגאומטרייה תמירה
4. התנועה קבועה ומקבילה למיכל
5. מצב מתמיד -
6. הזרימה מפותחת בתעלות התמירות -

דג”ח רק בכיוון על הבוכנה

נתון כי התנועה קבועה, כך שמתקיים שימור תנע על הבוכנה (). לכן, מהדג”ח, ומשימור תנע בכיוון :

כאשר הוא עומק המיכל. כיוון שהבעיה דו-ממדית, נתעלם ממנו (נניח שגודלו יחידת אורך יחידה):

בנוסף, מאחר והמסה אחידה, מתקיים :

נסמן , ונשים לב שזהו בעצם סך הכוח שהנוזל מפעיל על המוצק בדפנה.

כדי לחשב את , נביט באחת מהדפנות:

הדפנה הימנית בין המיכל והבוכנה

ממשוואת הרצף (בדו-ממד):

מתקיים גם תנאי האי חדירה בקצוות התעלה:

ולכן, טענה :

7. המהירות בכיוון בתעלה אפסית - .

מאחר והנחנו זרימה צמיגה, הגאומטרייה תמירה, והבעיה דו-ממדית, נוכל לקבוע כי זוהי פשוט זרימה סיכתית ללא הזנחת כבידה:

כמו בשאלות קודמות, נוכל להסיק כי המשוואה הראשונה פשוט שווה לקבוע:

לכן:

התנאי שפה הם פשוט ו-, ולכן:

ולכן:

נציב בחזרה בביטוי הקבוע:

נסמן את אגף ימין ב-. נקבל לאחר אינטגרציה פעמיים לפי :

תנאי השפה שלנו הם תנאי אי החלקה:

נציב בחזרה ב-:

נוכל כעת למצוא את מאמץ הגזירה שנוצר כתוצאה ממהירות זו. לפי טנזור מאמץ לנוזל ניוטוני:

לכן:

שזוהי פונקציית מאמץ הגזירה שמופעל על הנוזל. אכפת לנו רק ממאמץ הגזירה שפועל על הנוזל בדפנה הקרובה לבוכנה:

מאחר וזהו המאמץ שהבוכנה מפעילה על הנוזל, נסיק כי הוא הנגדי למאמץ שהנוזל מפעיל על הבכנה:

נציב בחזרה ב-:

נציב את הפרש הלחצים זה בהגדרה שלנו ל-:

נמצא עוד קשר בין מהירות המיכל , למהירות הזורם בדפנות, .

נפח בקרה משתנה עם הזמן - חלקו העליון מתקדם הצלע העליונה של הבכנה - במהירות . נפח הבקרה לא כולל את הבוכנה.

נבצע שימור מסה אינטגרלי:

מאחר והבעיה דו-ממדית:

הצפיפות אחידה לאורך כל נפח הבקרה ולכן נוכל לחלק בו:

השטח של נפח הבקרה תלוי בזמן:

השינוי בגובה הוא פשוט המהירות . נשים לב שהוא יהיה בסימן שלילי, כי קטן עם הזמן.

לגבי המהירות על שפת נפח הבקרה - ישנן שתי יציאות, שתיהן במהירות שחישבנו עבור התעלה. יחסית למהירות נפח הבקרה בגבול העליון, הן במהירות . נציב:

נציב את הביטוי שמצאנו ל- - :

מאחר ו-, נוכל להזניח אותו במקומות ספציפיים:

סעיף ב’

מבין כל ההנחות, היחידות שלא היו נתונות הן:

• הנחת הצמיגות:
  נבדוק שמספר ריינולדס קטן מאוד - . מאחר ומדובר בגאומטרייה תמירה (), מספיק לבדוק את התנאי על ריינולדס המוקטן: נמצא את גודל לפי הנתונים: נציב בתנאי, ונמצא כי אכן:
• זרימה מפותחת בתעלה:
  נוכל לבצע שימור מסה אינטגרלי על כל שני חתכים כלליים לאורך הקורה, ולמצוא כי: כך שלמעשה לא תלוי ב- - זרימה מפותחת.