פנגייה

HTF1_004 הולכה במצב לא מתמיד

• זמן קריאה: 12 דק'

מבוא

עד כה התעסקנו בבעיות חום במצב מתמיד, כך שבמשוואת החום תמיד איפסנו את . אבל, הרבה פעמים נרצה לדעת איך פילוג הטמפרטורה משתנה במרחב ובזמן. לשם כך נצטרך לפתח שיטה אחרת לפתירת הבעיה, כי כעת לא נוכל לאפס את הנגזרות לפי הזמן במערכת.

שיטת הקיבול המקובץ

בעיית חום נפוצה היא אחת בה מוצק כלשהו חווה שינוי פתאומי בסביבה התרמית שלו. קחו למשל מתכת חמה שהיא בהתחלה בטמפרטורה אחידה וברגע מסוים היא מחוסמת לטמפרטורה נמוכה יותר .
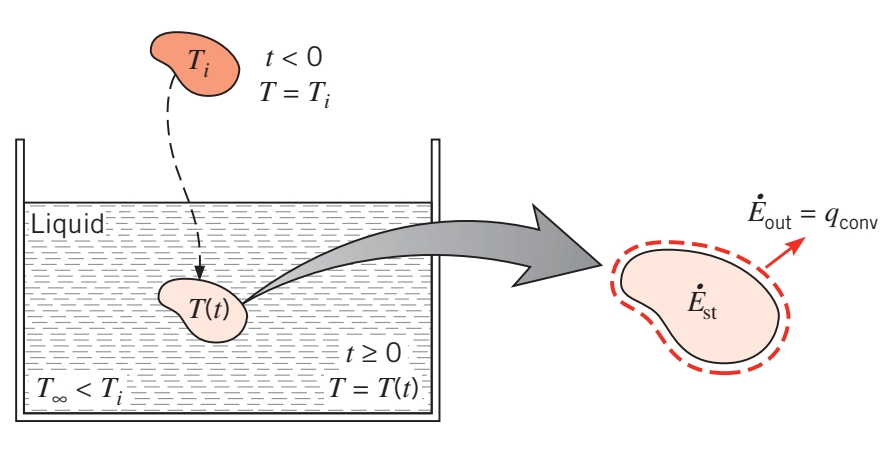
bookhue

קירור של מתכת חמה. (Bergman & Lavine, 2017).

בהנחה והחיסום התרחש ברגע , הטמפרטורה של המתכת תדעך לכל , עד שהיא תגיע ל-. דעיכה זו היא כתוצאה מהסעה של המעבר חום במגע בין המוצק והנוזל. העיקרון בשיטת הקיבול המקובץ היא ההנחה שהטמפרטורה של המוצק היא אחידה במרחב בכל רגע במהלך התהליך. מהנחה זו אנו יכולים להזניח את הגרדיאנטים של הטמפרטורה במוצק.

מחוק חוק פורייה, הולכת החום כאשר אין גרדיאנט טמפרטורה אומר שיש הולכה תרמית אינסופית. כמובן שתנאי זה לא אפשרי. אבל, תנאי זה ניתן לקירוב אם ההתנגדות להולכה בתוך החומר היא קטנה מספיק לעומת ההתנגדות למערכת חום בין המוצק לסביבה שלו. נגיע למתי מותר לנו להניח את הנחה זו בהמשך.

אם נזניח את את גרדיאנטי הטמפרטורות במוצק, לפי חוק ראשון על הנפח בקרה המוצגת לעיל תהיה מהצורה:

או פשוט:

כאשר הוא מקדם החום הסגולי בלחץ קבוע.
אם נסמן , נקבל לאחר פתירת המד”ר ש:

כאשר נשים לב שקיבלנו אקספוננט עם קבוע זמן תרמי:

כאשר ל- אנו קוראים קיבול חום תרמי ונסמנו , ו- הוא פשוט ההתנגדות להסעה שכבר ראינו בעבר.

עבור המקרה שבו , הגרף של פילוג הטמפרטורה ייראה מהצורה הבאה:
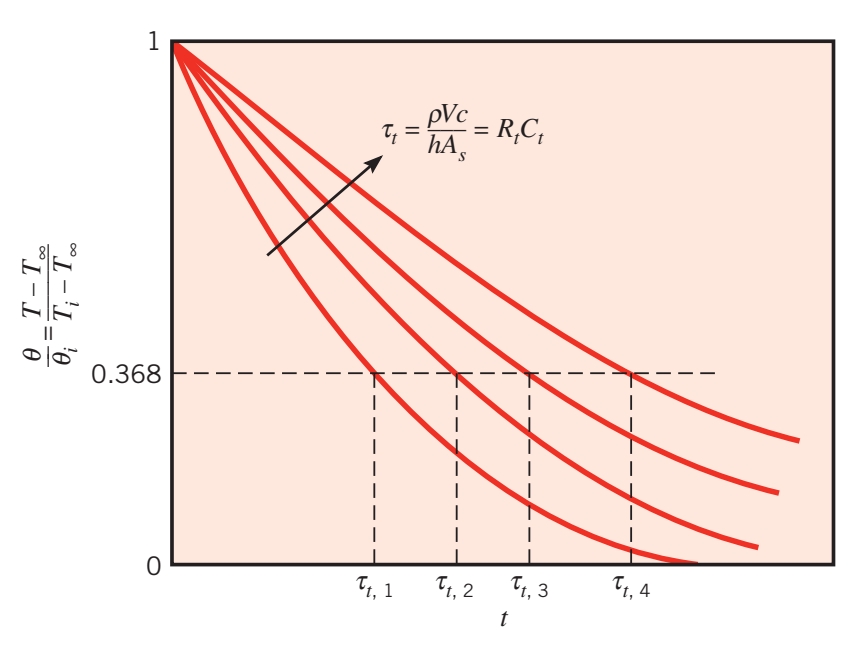
bookhue

תגובת מעבר לפי שיטת הקיבול המקובץ עבור קבועי זמן תרמיים שונים. (Bergman & Lavine, 2017).

מבחינת האנרגיה שעזבה את הגוף, נוכל לחשבה ע”י אינטגרציה על פילוג הטמפרטורה. נקבל ש:

מגבלות שיטת הקיבול המקובץ

בעוד שיטת הקיבול המקובץ פשוטה ונוחה לפתרון בעיות מעבר חום לא במצב מתמיד, היא לא כל כך מדויקת. אנו בעצם מזניחים את פילוג הטמפרטורה במרחב - אנו מניחים שהיא אחידה, מה שלא נכון כמעט תמיד. אבל, נוכל להגדיר לעצמנו קריטריון למתי השימוש בהנחה זו עדיין מביאה לנו תוצאות יחסית מדויקות, כי יש מקרים בהם הטמפרטורה במרחב כן נשאר כמעט אחיד ולכן לא כל כך ישפיע על התוצאות שלנו.

כדי לפתח את קריטריון זה, נביט בלוח הבא עם שטח :

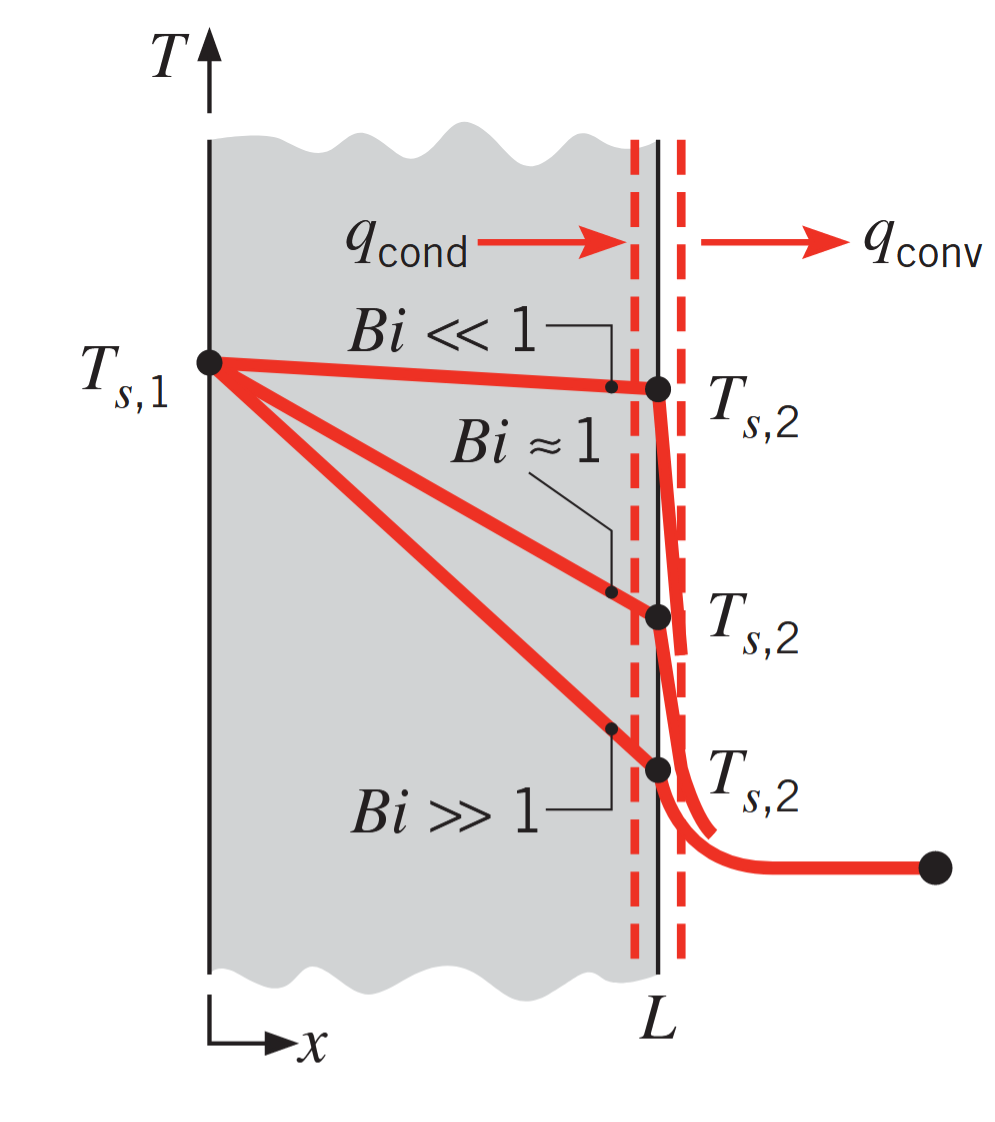
bookhue

השפעת מספר ביו על פילוג הטמפרטורה במצב מתמיד בלוח עם הסעה. (Bergman & Lavine, 2017).

למרות שאנו מניחים מצב מתמיד, ניתן להרחיב את הקריטריון שלנו גם למצבים לא מתמידים. משטח אחד של הלוח נשמר בטמפרטורה , בעוד משטח אחד חשוף לזורם בטמפרטורה . הטמפרטורה על משטח זה תהיה איזשהו ערך , שנמצא בין שתי הטמפרטורות, כלומר . לכן, תחת הנחות מצב מתמיד, ומשימור אנרגיה, קצב מעבר החום משטח למשטח אחד שווה לקצב מעבר החום מהזורם:

לביטוי בצד ימין יש שם:

הגדרה: מספר ביו

מספר ביו () על שם Jean-Baptiste Biot (כנראה לא מבטאים את ה-t בסוף כי הוא אוכל בגטים או משהו) מוגדר כ:

כאשר הוא אורך מתוקן.
זהו מספר חסר ממדי, והוא נותן לנו איזשהו כיוון על מידת הפרש הטמפרטורות במוצק ביחס להפרש הטמפרטורות בין פני המוצק לזורם. הוא גם פשוט היחס בין ההתנגדויות התרמיות.

לכן:
אם , ההתנגדות להולכה בתוך המוצק קטנה בהרבה מההתנגדות להסעה לאורך שכבת הגבול של הזורם. לכן, ההנחה של טמפרטורה אחידה בתוך המוצק תקפה אם מספר הביו קטן.

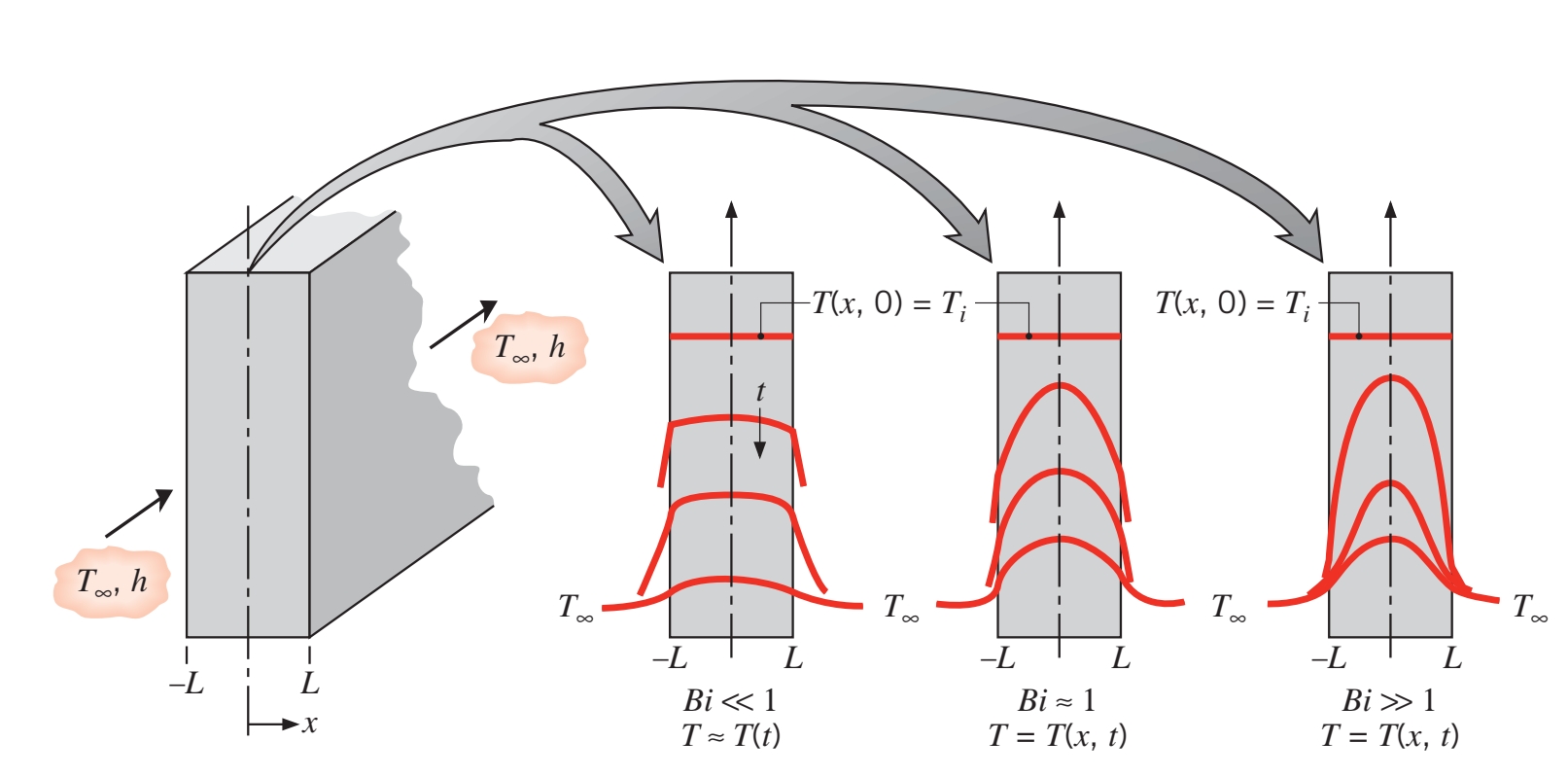
bookhue

פילוג טמפרטורות לא במצב מתמיד עבור מספרי ביו שונים בלוח המקורר סימטרית ע”י הסעה. (Bergman & Lavine, 2017).

במקרה הכללי, נחשב את מספר ביו באופן הבא:

כאשר נקרא האורך האופייני של המערכת, ולרוב נחשב אותו כהיחס בין הנפח של המוצק לשטח פנים . הגדרה זו דורשת את החישוב של למוצקים עם צורות גאומטריות מסובכות (לעומת המקרה הפשוט של לוח עם הסעה שהוא רק ).
למשל, במקרה המאויר לעיל של לוח המקורר סימטרית עם אורך , האורך האופייני הוא , כי יש שטח פנים החשוף להסעה משני הצדדים של הקיר. עבור גליל ארוך האורך האופייני הוא , ו- לכדור.
אם נדרש קריטריון טיפה יותר מחמיר, אפשר להגדיר את כאורך המתאים להפרשי הטמפרטורה המרחביים הכי גבוהים. לקיר המקורר סימטרית האורך האופייני עדיין נשאר , אבל עבור גליל ארוך או כדור הוא הופך להיות .

נשים לב שבמידה ו- , הביטוי בתוך האקספוננט בפילוג הטמפרטורה ניתן לביטוי כ:

כאשר:

הגדרה: מספר פורייה

המספר נקרא מספר פורייה:

כאשר הוא דִּיפוּזִיבִיּוּת (diffusivity) של החומר. מספר פורייה הוא מספר חסר יחידות, והוא מאפיין בעיות הולכה בזמן. הוא נותן הערכה כללית לזמן הנדרש לחום להתפזר במרחק אופייני כלשהו.

כעת, נוכל לרשום את המשוואה לפילוג החום בזמן גם כ:

שיטת הקיבול המקובץ הכללית

למרות שהולכה בזמן במוצק לרוב מתחילה מהסעה, ישנם תהליכים אחרים שיכולים לגרום לתחילת שינוי טמפרטורות עם הזמן במוצק. נביט במקרה הכללי שבו מוצק מושפע גם מהסעה, גם מקרינה, וגם משטף חום חיצוני דרך אחד מהמשטחים שלו, ונוסיף על זה גם ייצור חום.
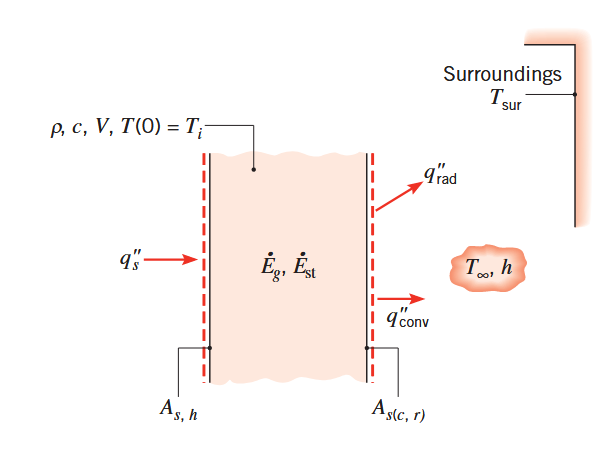
bookhue

נפח בקרה לשיטת הקיבול המקובץ הכללית. (Bergman & Lavine, 2017).

נניח שבהתחלה הטמפרטורה של המוצק שונה מזו של הזורם והסביבה , ושגם המשטח והחימום הנפחי ( ו-) קיימים. השטף חום החיצוני וההסעה מתרחשים במשטחים שונים, ו- בהתאמה, ואנו מניחים שההסעה היא מתוך המשטח. מעבר לכך, למרות שההסעה והקרינה הם מאותו המשטח, השטחים יכולים להיות שונים (). מחוק הראשון:

מחוק הקירור של ניוטון וחוק סטפן-בולצמן:

משוואה זו היא משוואה דיפרנציאלית חלקית לא לינארית, לא הומוגנית ומסדר ראשון. לא ניתן לבצע עליה אינטגרציה לקבלת פתרון מדויק. אבל, כן נוכל למצוא פתרונות מדויקים עבור מקרים פרטיים שלה.
למשל, אם נזניח קרינה, נסמן , כך שהמשוואה הופכת להיות מהצורה:

עם:

ונקבל שהפתרון הסופי הוא מהצורה:

השפעות מרחביות

במקרה בו המספר ביו לא קטן, אנו חייבים גם להתחשב בגרדיאנטי הטמפרטורה. ממשוואת ההולכה, במקרה המתואר באיור הבא, זה אומר:

bookhue

לוח סימטרי עם הולכה בצדדים. (Bergman & Lavine, 2017).

נחליף קואורדינטות:

כמו בזרימה, יהיה לנו יותר נוח לתאר את המשוואה בעזרת מספרים חסרי ממד. אצלנו, נבחר ב:

שימו לב!:

מספר פורייה ומספר ביו כפי שהם מוצגים עם אורך מתוקן בקיבול מקובץ תקפים רק עבור קיבול מקובץ! כאן אנו מגדירים אותם באופן שונה:

כאשר הוא מחצית מאורך הקיר, או פשוט רדיוס הכדור או הגליל.

כך שהמד”ח שלנו היא כעת:

נשים לב שזוהי בדיוק משוואת חום שפתרנו במד”ח, עם תנאי שפה:

^eq-5-39, 5-40

ותנאי ההתחלה:

בעצם המרנו את הבעיה שלנו לבעיה חסרת ממדים שהפתרון החסר ממדי שלה הוא מהצורה:

פתרון מדויק

פתרונות אנליטיים למעבר חום בזמן קיימים למספר גאומטריות פשוטות ותנאי שפה. מספר טכניקות מתמטיות, בהן שיטת הפרדת משתנים, משומשים למטרה זו, ולרוב מוצגים באופן חסר ממדי, ומורכבים מטור אינסופי. אבל, חוץ מעבור מספרים מאוד קטנים של מספר פורייה , טור זה ניתן לקירוב ע”י ביטוי יחיד מהטור.

נביט במערכת הבאה:
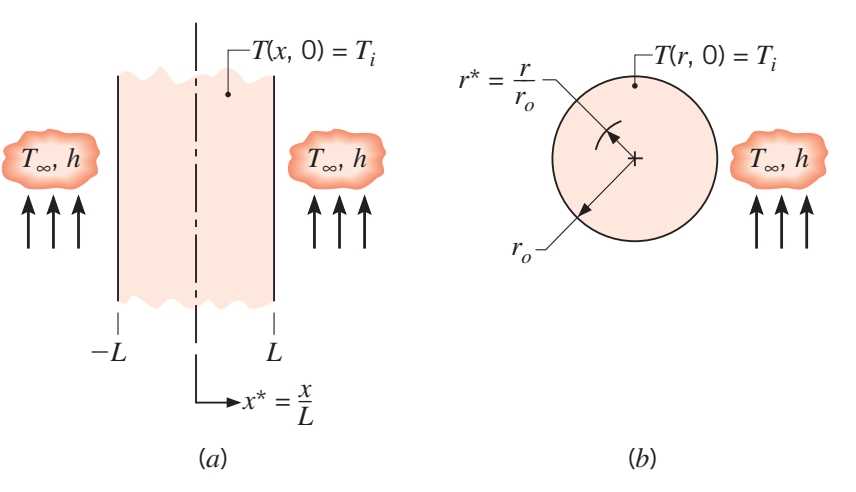
bookhue

מערכת חד ממדית עם טמפרטורה אחידה התחלתית הנתונה לתנאי הסעה בפתאומיות. (a) לוח פשוט; (b) גליל אינסופי או כדור. (Bergman & Lavine, 2017).

אם העובי קטן יחסית לרוחב והגובה של הקיר, אפשר להניח שההולכה מתרחשת רק בכיוון . אם הקיר בהתחלה בטמפרטורה אחידה, ופתאום נטבל בזורם בטמפרטורה , משוואות מתארות את בעיה זו לחלוטין. כיוון שתנאי ההסעה בפני השטח ב- הם זהים, פילוג הטמפרטורה בכל רגע נתון יהיה סימטרי סביב .

פילוג הטמפרטורה המתקבל מפתרון אנליטי הוא:

כאשר המקדם הוא:

עם הע”ע שהם השורשים החיוביים של המשוואה:

ארבעת השורשים הראשונים למשוואה זו נתונים ב-HTF1_A5 טבלאות להולכה במצב לא מתמיד. הפתרון המדויק ב-(IH5.42a) תקף לכל זמן .

קירוב לפתרון

ניתן להראות שעבור ערכי (כלומר, עבור פרקי זמן ארוכים), הטור האינסופי בפתרון (IH5.42a) ניתן לקירוב ע”י הביטוי הראשון בטור, . עם קירוב זה, פילוג הטמפרטורה החד ממדי בקיר הופך להיות:

או:

כאשר הוא הטמפרטורה ב- :

מסקנה חשובה מ-(IH5.43b) היא שהתלות בזמן של הטמפרטורה בכל מקום בלוח היא זהה לזו של אמצע הלוח (). את המקדמים ו- ניתן למצוא גם ב-טבלה 5.1, כאשר לפי ההערה בתחתית הטבלה, משתמשים במספר מוחמר (המספר הרלוונטי הופך להיות עבור לוח פשוט, ו- עבור כדור וגליל).

במקרה ומדובר בגליל, הקירוב לפתרון הוא:

כאשר ו- . עבור כדור:

הגדלים ו- הם פונקציות בסל (Bessel functions) מהסוג הראשון, וערכיהם נתונים בטבלה B.4.

סך מעבר אנרגיה

בהרבה מן המקרים נרצה לדעת מהו סך האנרגיה שנשארה (או נכנסה) לקיר עד זמן כלשהו . מחוק הראשון של התרמודינמיקה, כאשר אין ייצור חום:

נשווה את האנרגיה המועברת מהקיר ל-, ומהנחה ואין אנרגיה שנכנסת . נישאר עם:

כאשר האינטגרציה מתבצעת לאורך נפח הקיר.

מוצק חצי אינסופי

עבור פרקי זמן מאוד קצרים, , נוח לנו לבצע קירוב אחר לגופים שאנו איתם עובדים: הנחת החצי אינסופיות. בהנחה זו אנו מניחים שהגוף ממשיך לאינסוף בכיוון אחד משפת הגוף. אם חל שינוי פתאומי בתנאים על שפת הגוף, הולכה חד ממדית תתרחש בכיוון זה.

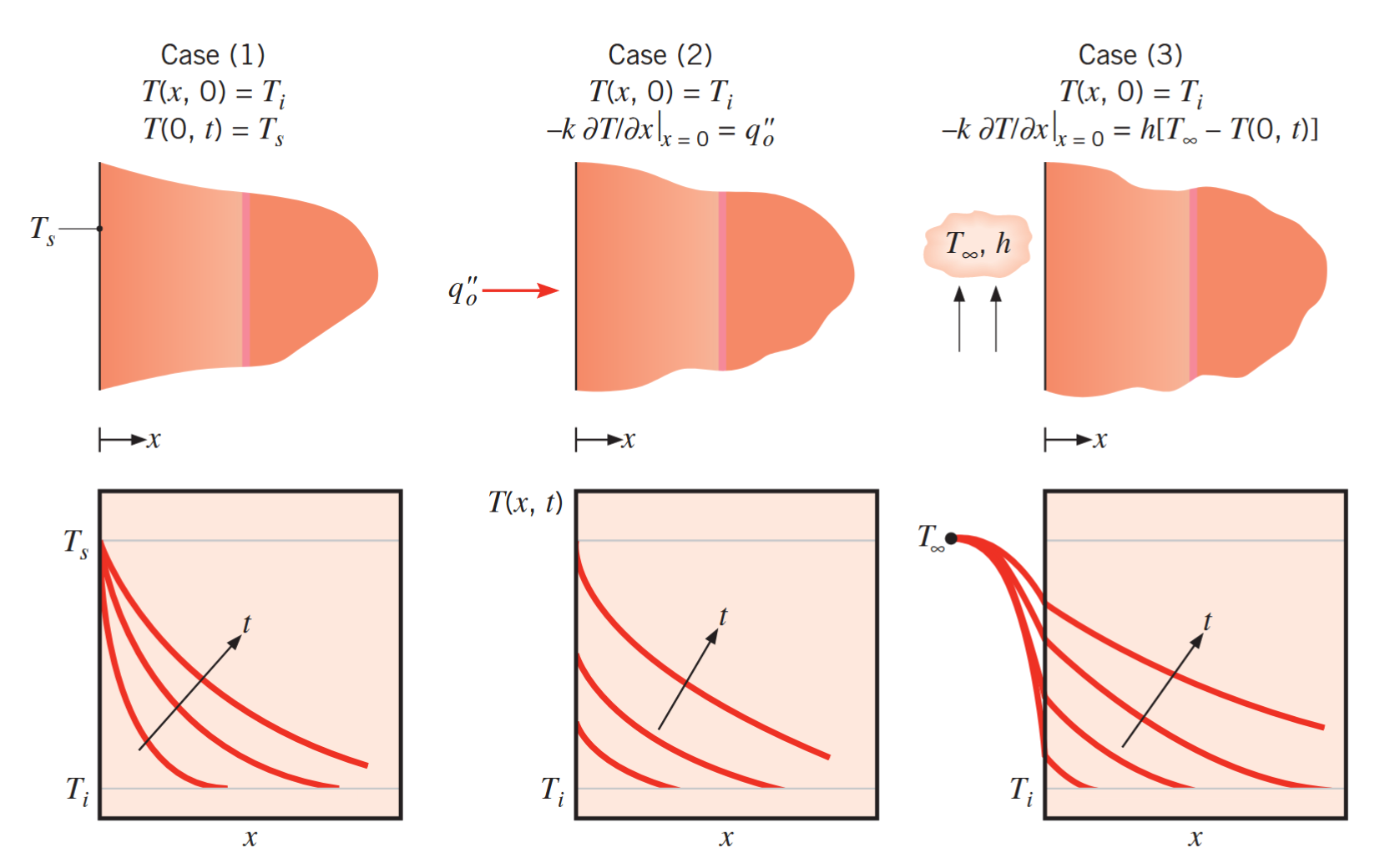
bookhue

פילוג טמפרטורות במוצק חצי אינסופי במצב לא מתמיד, עבור שלושה תנאי שפה (משמאל לימין): טמפרטורה אחידה, שטף חום אחיד, ומעבר חום בהסעה. (Bergman & Lavine, 2017).

מוצק חצי אינסופי הוא בעצם אידיאליזציה להמון בעיות, בהן בתחילת תהליך המעבר (transient) המוצק הפנימי יותר (הרחוק מהשפה) עדיין לא מרגיש את השינוי בשפת המוצק. כלומר, אנו מניחים ש:

עם הנחה זו ניתן לקבל פתרונות אנליטיים לפילוג הטמפרטורה, שהם די מדויקים עבור . פיתוח הפתרונות עצמן הוא ארוך ומייגע, אז נסתפק רק בתוצאות הסופיות של תנאי השפה השונים:

  1. טמפרטורה אחידה בשפה ():
  2. שטף חום אחיד בשפה ():
  3. הסעה בשפה ():

הפונקציות ו- נקראות פונקציית השגיאה (error function) ופונקציית השגיאה המשלימה (complementary error function) בהתאמה, והן מוגדרות באופן הבא:

תרגילים

תרגיל 1

בקו ייצור, לוחות גדולים בעובי מפליז (צפיפות , חום סגולי ומוליכות תרמית ) מוכנסים לתנור בטמפרטורה של למשך זמן רב לפני הוצאת לקירורם בתהליך של חיסום. מצא את פרק הזמן מרגע הוצאת מהתנור והטבלתו במים (טמפרטורת מים ומקדם מעבר חום בהסעה ) עד ש:

  • הטמפרטורה במרכז הלוח תרד ל-.
  • הלוח יאבד מהסה”כ עודף האנרגיה ההתחלתית האצורה בו ביחס לסביבה.
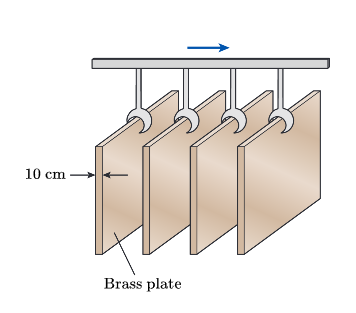
    bookhue

    סכמת הבעיה. (Çengel et al., 2024).

סעיף א’

  • הטמפרטורה במרכז הלוח תרד ל-.

פתרון:
זוהי שאלה של שינוי בזמן ולכן קודם כל נבדוק .

קיבלנו ש- , ולכן נוכל להניח שהטמפרטורה אחידה בכלל הגוף. לפיכך, הטמפרטורה תלויה רק בזמן, ונוכל להשתמש במשוואת החום בצורת הפשוטה:

התנאי התחלה שלנו הוא . נקבל כי , כך ש:

ולכן:

נמצא כי אם:

כאשר הוא הוא הפרש הטמפרטורות כאשר , כלומר:

נציב ונקבל:

סעיף ב’

  • הלוח יאבד מהסה”כ עודף האנרגיה ההתחלתית האצורה בו ביחס לסביבה.

פתרון:
פוטנציאל החום מוגדר ככמות החום שיכולה להשתחרר מהלוח:

נאבד מהאנרגיה כאשר:

נציב נתונים ונקבל:

תרגיל 2

מיכל גלילי, דק דופן, בקוטר , ומבודד בשני בסיסיו, מכיל נוזל בעל צפיפות וחום סגולי . כתוצאה מתגובה כימית בתוך המיכל, תוך כדי ערבוב מתמיד של הנוזל, נוצר חום אחיד בנפח המיכל בקצב . כמו כן, המיכל חשוף לאוויר בטמפרטורה ומקדם מעבר חום בהסעה . טמפרטורת הנוזל ההתחלתית הינה . יש לחשב את טמפרטורת הנוזל כעבור שעתיים.

פתרון:
נתון שהנוזל מעורבב באופן מתמיד, ולכן אין פילוג טמפרטורה מרחבית בתוך הגליל. לפיכך, נוכל להשתמש במשוואה:

הנפח הוא , בעוד השטח הוא , ולכן:

הפתרון ההומוגני של המד”ר:

פתרון פרטי:

לכן:

התנאי התחלה הוא , ולכן:

כך שהפתרון שלנו הוא:

מכאן נוכל למצוא שהטמפרטורה לאחר (שעתיים) היא:

עמודים המציינים את העמוד הזה