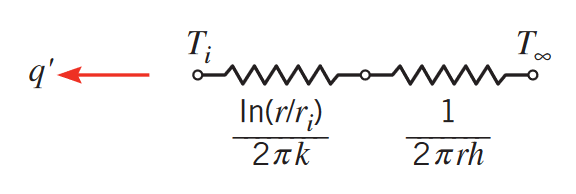HTF1_002 הולכה חד-ממדית במצב מתמיד

→ קודם: HTF1_001הבא: HTF1_003 ←

משוואת ההולכה

מטרה עיקרית בניתוח הולכה הוא למצוא את שדה הטמפרטורות בתווך מסוים, בעזרת תנאי שפה. כלומר, אנו רוצים לדעת מהו פיזור הטמפרטורות בנפח מסוים לאורך הזמן. בעזרת שדה זה, נוכל למצוא את קצב המעבר חום לפי חוק פורייה.

משפט:

משוואת ההולכה קושרת בין פיזור החום בנפח בקרה מסוים לקצב המעבר חום של הנפח בקרה דרך גבולותיו:

כאשר:

• הביטוי הוא שדה הטמפרטורה של נפח הבקרה.
• הביטוי הוא קצב ייצור החום הנפחי.
• הפרמטר הוא המוליכות התרמית של החומר (בגרסה זו של המשוואה אנו מניחים שהוא קבוע).
• הפרמטר נקרא הדיפוזיביות תרמית של החומר והוא שווה ל-.

בקואורדינטות קרטזיות:

במילים, המשוואה הזאת טוענת שבכל נקודה בתווך, סך קצב מעבר האנרגיה ע”י הולכה לתוך יחידת נפח ועוד קצב יצירת האנרגיה חייב להיות שווה לקצב שינוי האנרגיה התרמית בתוך הנפח בקרה. עכשיו בדיעבד אני קולט שכנראה אי אפשר לעקוב אחרי המשפט הזה.

פיתוח:
כדי לפתח את משוואת ההולכה, נביט בנפח בקרה דיפרנציאלי, כפי שמתואר באיור הבא:

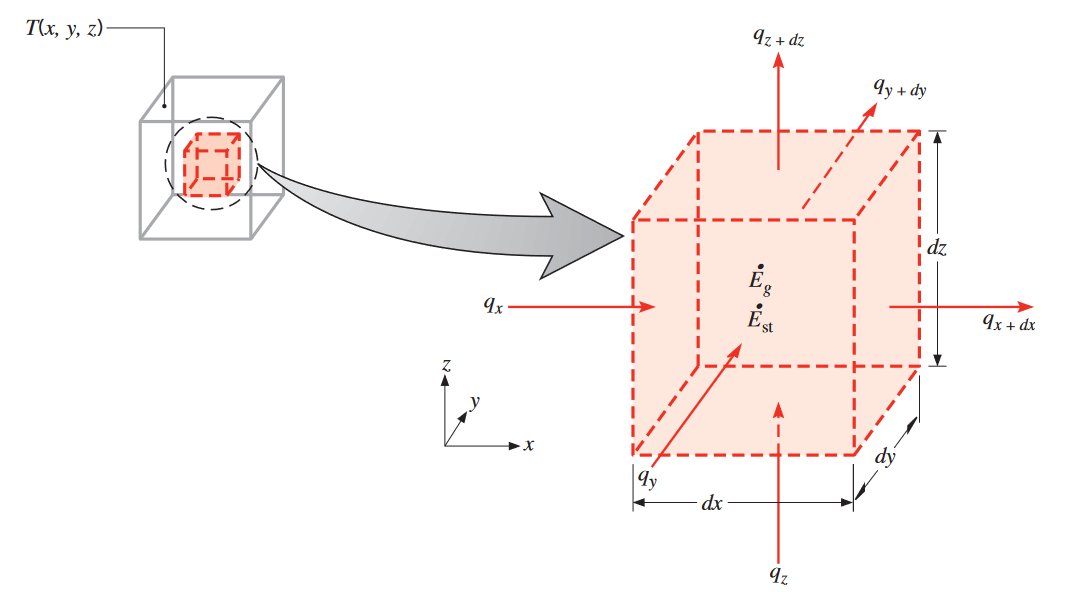
נפח בקרה דיפרנציאלי בקואורדינטות קרטזיות. (Bergman & Lavine, 2017).

נניח והתווך לא דחיס, כך שהצפיפות לאורך התווך אחידה. בנוסף, נניח גם שאין תנועת זורם, ושפיזור הטמפרטורה נתון בקואורדינטות קרטזיות.
נרצה לרשום כעת את חוק ראשון עבור הנפח בקרה הזה. בהיעדר תנועה, אין שינויים באנרגיה המכנית ושום עבודה לא מתבצעת על המערכת. רק השינויים באנרגיה התרמית צריכים להילקח בחשבון. בפרט, אם יש גרדיאנטים בטמפרטורה, מעבר חום בהולכה יתרחש לאורך כל אחד מהמשטחי בקרה (לאורך הגבול של הנפח בקרה). קצבי ההולכה בכל אחד מהכיוונים מסומנים לפי הציר המאונך למשטח הבקרה הרלוונטי - . קצב ההולכה במשטחים הנגדיים אליהם מוצגים כפיתוח טיילור של , עם הזנחת איברים מסדר גבוה:

במילים, משוואה המשוואה הראשונה אומרת שרכיב ה- של קצב המעבר חום דרך משטח שווה לערך של רכיב זה ב- (כלומר, ), ועוד הכמות בה הוא משתנה בכיוון ,כפול (כלומר, ).

בתוך התווך יכל להיות גם ביטוי למקור אנרגיה הגורם לייצור אנרגיה תרמית. את הביטוי נוכל לרשום כ:

כאשר הוא הקצב בו האנרגיה נוצרת ליחידת נפח ().
בנוסף, שינויים עלולים להתרחש בכמות של האנרגיה התרמית הפנימית בחומר בנפח בקרה. אם בחומר לא חל שינוי בפאזה, אז אין שינויים באנרגיה הכמוסה של החומר, כך שבביטוי אנרגיית הגוף נישאר רק עם השינויים באנרגיה המוחשת :

כאשר השתמשנו בהנחה ש- בחומר בלתי דחיס ( ו- הם הקיבולי החום של החומר).

נרצה כעת להציב את המשוואות שמצאנו בחוק הראשון של התרמודינמיקה, בנגזרת שלו לפי הזמן:

נשים לב שמעצם ההגדרה:

נציב בחזרה בחוק ראשון:

נוכל להציב את הביטויים עבור כדי לקבל:

מחוק פורייה נסיק כי קצב המעבר חום בכל אחד מהכיוונים הוא:

כאשר כל ביטוי שטף חום הוכפל בשטח הדיפרנציאלי המתאים. נציב את שלושת משוואות אלו בחזרה בחוק ראשון כדי לקבל:

משוואה זו נקראת משוואת ההולכה (או משוואות החום, heat diffusion equation) בצורתה הכללית, בקואורדינטות קרטזיות. אם ההולכה התרמית קבועה, נוכל לפשט את המשוואה לצורה:

כאשר נקרא דיפוזיביות תרמית.
כדי שנוכל להכליל למערכות קואורדינטות אחרות, נוכל לרשום את המשוואה גם בעזרת הלפלסיאן:

דוגמה:

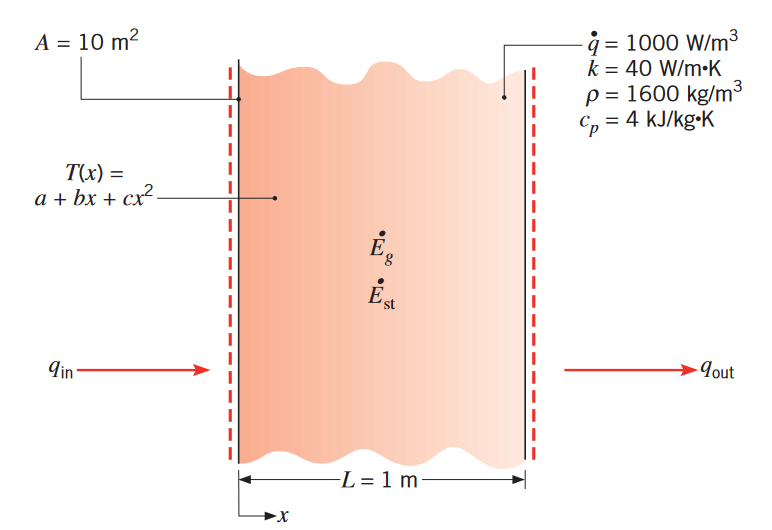
פילוג הטמפרטורה לאורך קיר בעובי ברגע מסוים בזמן נתון כ:

כאשר במעלות צלזיוס ו- במטרים. בנוסף, , , ו- . קיים ייצור חום פנימי אחיד על הקיר בעל שטח , עם התכונות ו-.

סכמת הבעיה. (Bergman & Lavine, 2017).

1. מצאו את קצב המעבר חום הנכנס דרך הקיר () ושעוזב את הקיר .
2. מצאו את קצב השינוי של האנרגיה האגורה בקיר.
3. מצאו את קצב שינוי הטמפרטורה ב- ו-.

פתרון:
הנחות:

1. הולכה חד-ממדית בכיוון .
2. תווך איזוטרופי, בלתי דחיס, עם תכונות אחידות.
3. ייצור חום פנימי אחיד, .

לפי סעיפים:

1. אנו יודעים שברגע שפילוג הטמפרטורה ידוע עבור תווך מסוים, נוכל פשוט להציב את כל הנתונים ישירות בחוק פורייה:

באותו אופן:

ולכן:

2. קצב השינוי של מאגר האנרגיה בקיר ניתן לחישוב בעזרת מאזן אנרגיה (חוק ראשון) על הקיר:

כאשר . לכן:

ולכן:

3. קצב השינוי של הטמפרטורה בכל נקודה בתווך ניתן לחישוב בעזרת משוואת החום, עם קצת העברת אגפים:

מהנתון על פילוג הטמפרטורה:

נשים לב שהנגזרת הזאת לא תלויה במיקום בתווך. לכן, קצב השינוי של הטמפרטורה גם כן לא תלויה במיקום. נציב בחזרה במשוואת החום:

ולכן:

תנאי התחלה ושפה

כדי למצוא את פילוג הטמפרטורה בתווך מסוים, דרוש לפתור את המשוואת חום המתאימה. אבל, פתרון כזה תלוי בתנאי השפה של התווך, ואם הבעיה תלויה בזמן, אז הוא גם תלוי בתנאי התחלה. מאחר ומשוואת החום היא מסדר שני ביחס למרחב, נדרש שני תנאי שפה בכל קואורדינטה הדרושה כדי לתאר את המערכת. עבור תנאי ההתחלה, נדרש רק אחד, כי המשוואה היא ממעלה ראשונה ביחס לזמן.

ישנם 4 תנאי שפה בסיסיים שניתקל בהם:

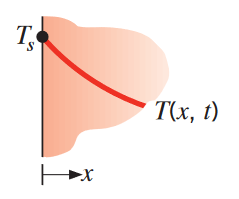			טמפרטורה קבועה
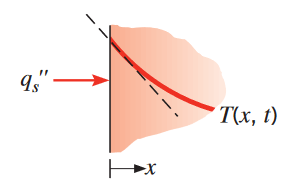		שטף חום סופי	שטף חום קבוע
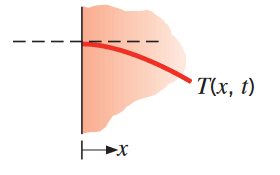		משטח מבודד
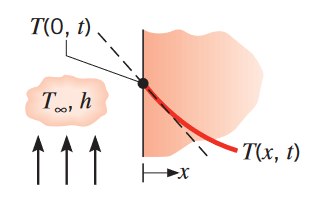			הסעה על המשטח

דוגמה:

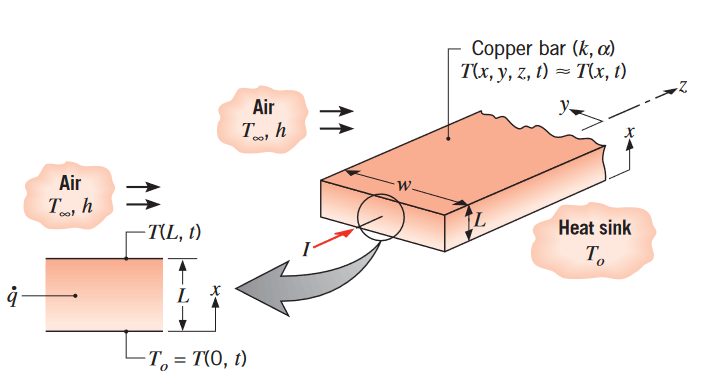
מוט נחושת ארוך עם שטח חתך מלבני, שרוחבו הרבה יותר גדול מהעובי שלו , נמצא במגע עם גוף קירור בפאה התחתונה שלו, והטמפרטורה לאורך המוט היא שווה בערך לטמפרטורה של הגוף קירור, . פתאום, זרם חשמלי עובר דרך המוט וזרם אוויר בטמפרטורה עובר מעל הפאה העליונה שלו, כאשר הפאה התחתונה נשארת במגע עם הגוף קירור.
מצאו את המשוואה הדיפרנציאלית, תנאי ההתחלה ותנאי השפה שנדרשים כדי למצוא את פילוג הטמפרטורה של המוט כפונקציה של מקום וזמן.

סכמת הבעיה. (Bergman & Lavine, 2017).

פתרון:
הנחות:

1. מאחר והמוט ארוך וגם , נזניח אפקטי קצה, כך שהמעבר חום במוט הוא בעיקר חד ממדי ובכיוון .
2. ייצור חום אחיד אחיד, .
3. התכונות הנתונות קבועות.

פילוג הטמפרטורה נשלט ע”י משוואת החום, שבמקרה שלנו היא מהצורה:

תנאי השפה בפאה התחתונה הוא טמפרטורה קבועה:

בפאה העליונה, יש הסעה על המשטח:

תנאי ההתחלה נובע מההכרה שלפני השינוי בתנאים, המוט היה בטמפרטורה אחידה :

כעת, בעזרת כלים ממד”ח ניתן לפתור את הבעיה כדי למצוא את .

לוח פשוט

נעבור כעת לשיטות פתרון משוואת החום החד-ממדית - כלומר, שגרדיאנט הטמפרטורה קיים רק בממד אחד (ולכן גם קצב המעבר חום מתרחש רק בכיוון אחד).

באיור הבא, לוח פשוט מפריד בין שני זורמים בעלי טמפרטורה שונה. מעבר חום בהסעה מתרחש מהזורם החם ב- אל צד אחד של הקיר ב-, בהולכה דרך הקיר, ובהסעה אל הצד השני של הקיר ב-, אל הזורם הקר ב-:

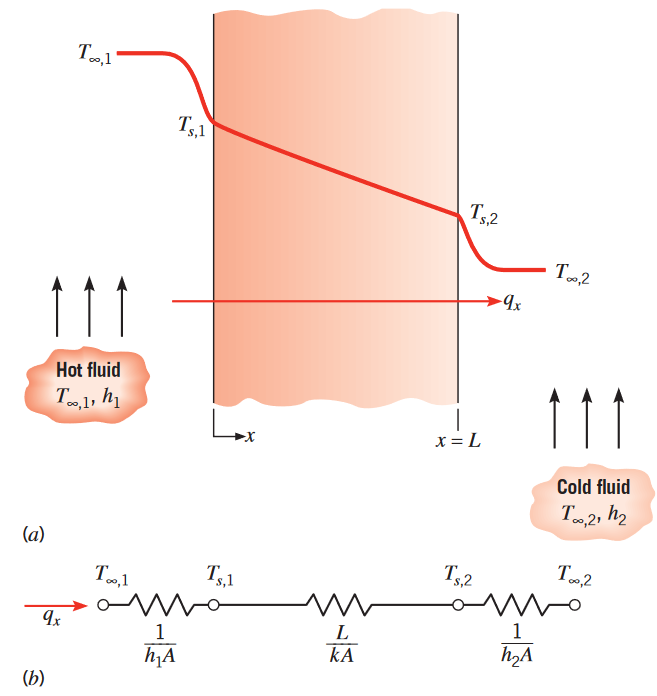
מעבר חום דרך לוח פשוט. (a) פילוג טמפרטורות. (b) מעגל תרמי שקול. (Bergman & Lavine, 2017).

כדי למצוא את קצב ההולכה, נתחיל מהתנאים בתוך הקיר. נמצא את פילוג הטמפרטורה, שממנו נוכל למצוא את קצב ההולכה.

פילוג הטמפרטורה

עבור מצב מתמיד, ללא מקור או “בור” אנרגיה בקיר (כלומר ללא ייצור חום פנימי במערכת), משוואת החום במקרה החד-ממדי היא:

ניתן להסיק מכך שעבור הולכה חד-ממדית, במצב מתמיד בלוח פשוט ללא ייצור חום פנימי, שטף החום הוא קבוע, ולא תלוי ב-.

אם ניתן להניח שההולכה התרמית של הקיר היא קבועה, ניתן לרשום את המשוואה בצורה הפשוטה יותר:

ואז הפתרון יהיה (לאחר אינטגרציה פעמיים) מהצורה:

כדי למצוא את הקבועים נשתמש בתנאי שפה:

לאחר הצבתם נקבל כי:

בעזרת פילוג הטמפרטורה נוכל למצוא את קצב מעבר חום לפי חוק פורייה:

התנגדות תרמית

נביט שוב בפילוג הטמפרטורה שקיבלנו עבור הקיר המישורי:

ממשוואה זו נובע קשר מאוד הדוק בין דיפוזיה של חום להתנגדות חשמלית. כמו שבהתנגדות חשמלית קשור להולכה החשמלית של החומר, נוכל לקשור בין התנגדות תרמית להולכה שלו. אם נגדיר את ההתנגדות התרמית כהיחס בין הפוטנציאל המניע את ההולכה לקצב המעבר חום, נסיק כי ההתנגדות התרמית להולכה של לוח פשוט הוא:

כאשר הממדים שלו הם:

באותו אופן, בהולכה חשמלית, חוק אוהם מתאר התנגדות חשמלית מהצורה:

נוכל באותו אופן גם להגדיר את ההתנגדות תרמית להסעה במשטח מסוים. מחוק הקירור של ניוטון:

כך שההתנגדות התרמית להסעה היא:

מעגלים הם כלי מעולה לתיאור בעיות מעברי חום. המעגל התרמי השקול לקיר המישורי מתואר באיור הקודם. את קצב מעבר החום נוכל למצוא מניתוח של כל חלק במעגל בנפרד. מאחר ו- קבוע לאורך המעגל, נסיק כי:

במובנים של הפרשי טמפרטורה כלליים, , והתנגדות תרמית כוללת, , נוכל לרשום את קצב מעבר החום בצורה:

כמו בחשמל, אנו יכולים לסכום את ההתנגדויות ההולכה וההסעה בטור כדי לקבל:

נוכל גם להגדיר התנגדות תרמית לקרינה, בעזרת חוק סטפן-בולצמן:

כאשר, ממשוואה (IH1.9):

לוח מעורב

נוכל להיעזר במעגלים תרמיים שקולים עבור מערכות יותר מסובכות, כמו לוח מעורב. קירות כאלה עלולים לכלול מספר התנגדויות תרמיים המחוברים בטור או במקביל כתוצאה משכבות של חומרים שונים.

נביט למשל לוח המעורב הבא:

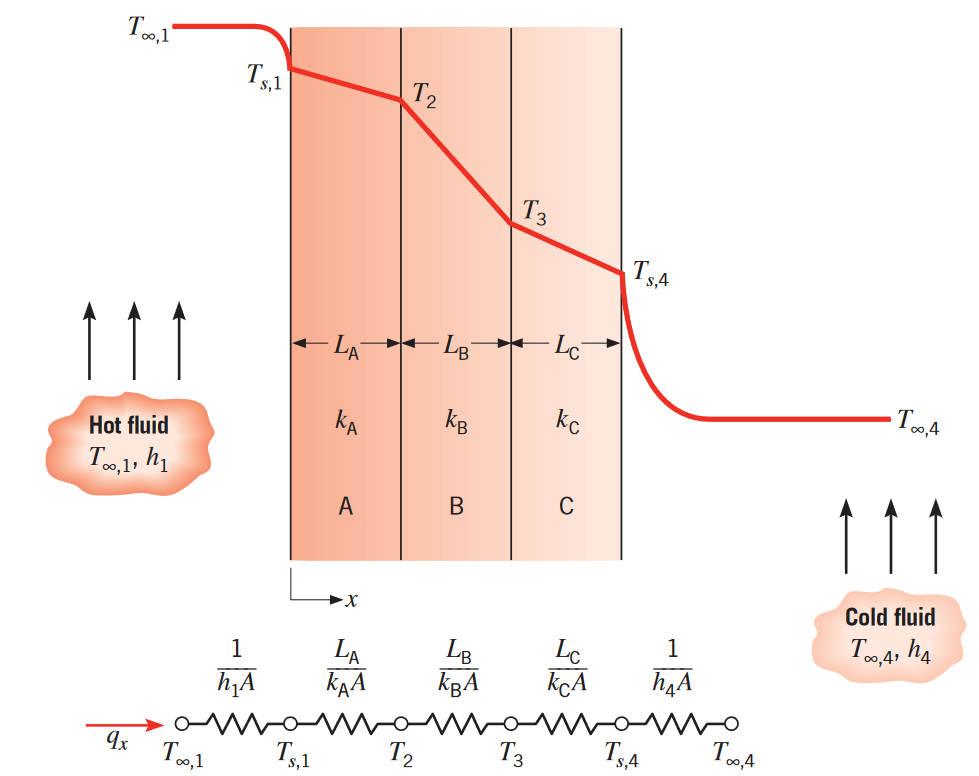
מעגלים תרמיים שקולים ללוח מעורב טורי. (Bergman & Lavine, 2017).

המעבר חום החד ממדי ניתן לביטוי כ:

כאשר הוא הפרש הטמפרטורות הכללי, וסך ההתנגדות התרמית היא סך כל ההתנגדויות, כך ש:

כאלטרנטיבה, ניתן לקשר בין הפרש הטמפרטורות וההתנגדות של כל רכיב בנפרד:

במערכות מעורבות, לרוב נוח לעבוד עם מקדם מעבר חום כללי, , שמוגדר בעזרת ביטוי מהצורה של חוק הקירור של ניוטון:

כאשר הוא הפרש הטמפרטורות הכללי. נוכל לקשור בין להתנגדות התרמית הכוללת:

באופן כללי, נוכל לרשום:

לוחות מעורבים יכולים לכלול נגדים תרמיים המחוברים בטור ובמקביל, כפי שמתואר באיור הבא:

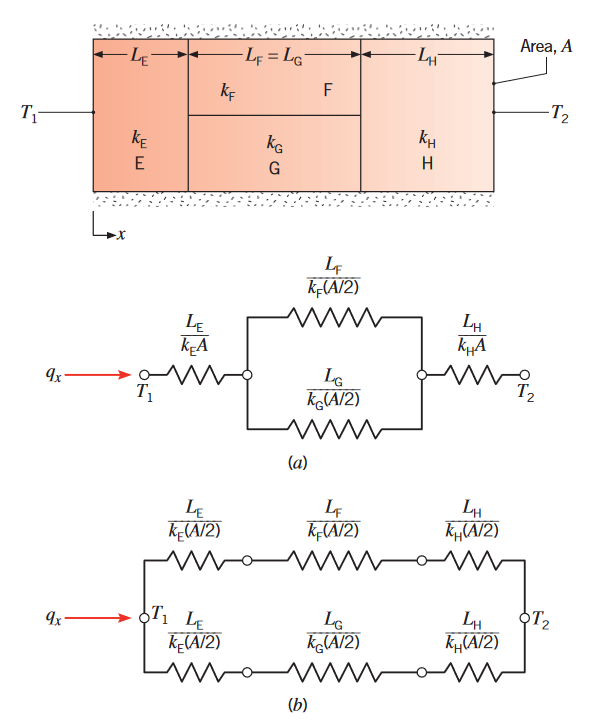
מעגלים תרמיים שקולים ללוח מעורב. (Bergman & Lavine, 2017).

למרות שהמעבר חום הוא כעת רב-ממדי, לרוב עדיין נוכל להניח תנאים חד-ממדיים. תחת הנחה זאת, נוכל לפתח שני מעגלים תרמיים שונים. עבור מקרה (a), אנו מניחים שהמשטחים הנורמליים לכיוון הם איזותרמיים, בעוד במקרה (b) אנו מניחים שהמשטחים המקבילים לכיוון הם אדיאבטיים.

התנגדות מגע

למרות שהזנחנו זאת עד כאן, חשוב להכיר שבמערכות מעורבות, מפל הטמפרטורה לאורך המשטח מגע בין החומרים צריך להילקח בחשבון. הפרש טמפרטורה זה משויך למה שנקרא התנגדות מגע תרמית, . האפקט הזה מתואר באיור הבא:

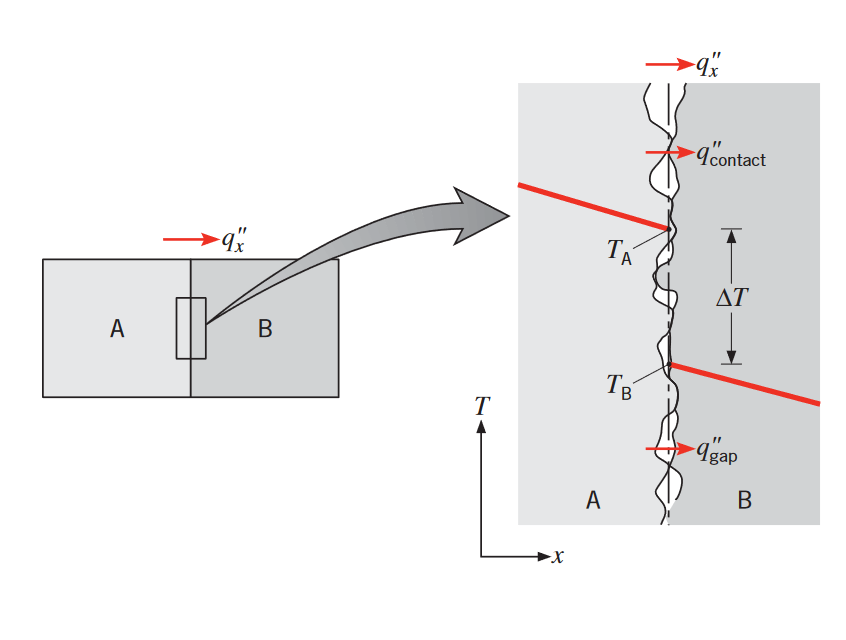
מפל טמפרטורה כתוצאה מהתנגדות מגע תרמית. (Bergman & Lavine, 2017).

הגדרה: התנגדות מגע תרמית

עבור יחידת שטח של המשטח מגע, ההתנגדות מגע תרמית מוגדרת כ:

הקיום של התנגדות מגע סופית היא כתוצאה מהחספוס של המשטח. בין הנקודות מגע של שני החומרים קיים לרוב אוויר, כך שמעבר החום כתוצאה מהולכה דרך נקודות המגע, והולכה/קרינה דרך המרווחים.

כדי לשפר את המגע התרמי בין הלוחות (כלומר, כדי להוריד את ההתנגדות מגע), נהוג לשים משחה תרמית (גריז, שמן וכו’) במגע בין החומרים, כך שההולכה התרמית במרווחים בין החומרים תשתפר. עבור מוצקים שההולכה התרמית שלהם גבוהה יותר מההולכה התרמית של המשחה התרמית, ניתן להקטין ההתנגדות התרמית ע”י הגדלת נקודות המגע בין המוצקים. ניתן לבצע זאת ע”י הגדלת לחץ המגע ביניהם, או ע”י החלקה של המשטחים כדי לקבל טיב פני שטח יותר טוב.

מערכות רדיאליות

במערכות רדיאליות - גליליות או ספריות, גרדיאנט הטמפרטורה עלול להתפשט רק בכיוון הרדיאלי, כך שנוכל להתייחס אליהם כחד-ממדיים.

קיר גלילי

דוגמה נפוצה היא גליל חלול שמשטחו הפנימי והחיצוני חשופים לזורמים בטמפרטורות שונות:

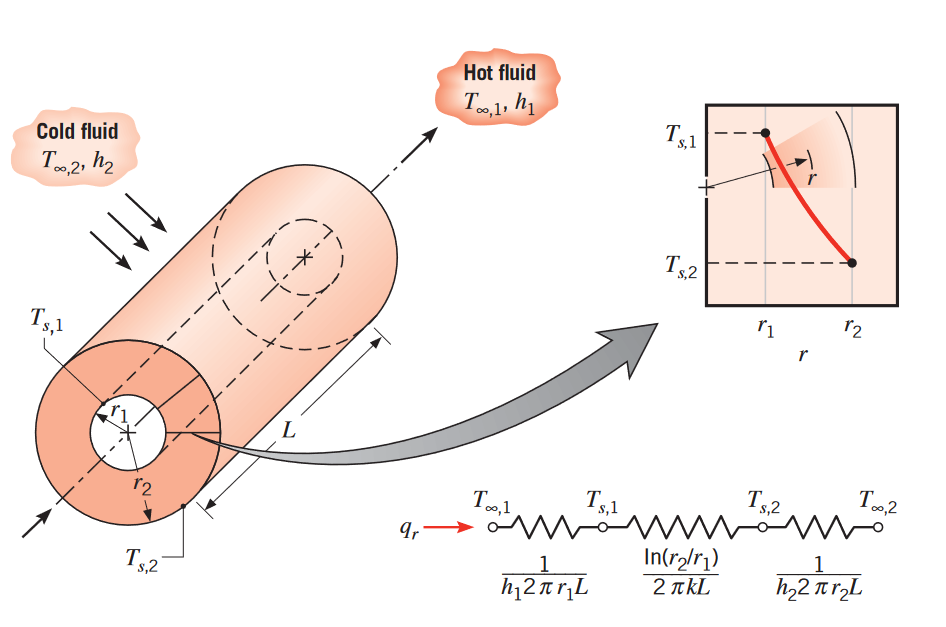
גליל חלול עם תנאי שפה של הסעה. (Bergman & Lavine, 2017).

במצב מתמיד, ללא ייצור חום, משוואת החום החד-מדדית בקואורדינטות פולאריות (בכיוון הרדיאלי) היא:

לכן, לפי חוק פורייה, קצב האנרגיה שמולך לאורך כל משטח גלילי בתוך המוצק ניתן לביטוי כ:

כאשר הוא השטח הניצב לכיוון המעבר חום. ממשוואת החום אנו יכולים להסיק שהגודל לא תלוי ב-, ולכן, מהביטוי עבור (קצב המעבר חום), נסיק כי קבוע בכיוון הרדיאלי.

בהנחה ו- קבוע, נוכל לפתור את משוואת החום כדי לקבל:

כדי לקבל את קבועי האינטגרציה ו- נציב תנאי שפה:

ונקבל כי:

נוכל להשתמש בחוק פורייה כדי לקבל את קצב המעבר חום:

מתוצאות אלו נסיק כי עבור הולכה רדיאלית בקיר גלילי, ההתנגדות התרמית היא מהצורה:

נביט כעת במערכת המעורבת הבאה:

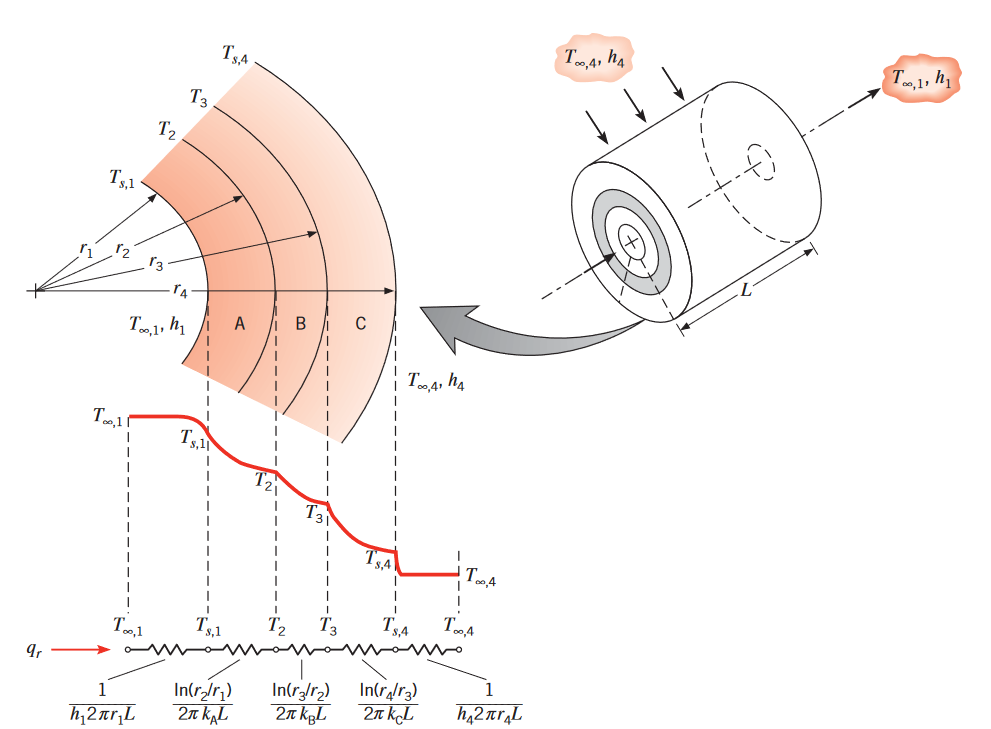
פילוג טמפרטורה לקיר הגלילי. (Bergman & Lavine, 2017).

באותו אופן כמו בלוח מעורב, קצב המעבר אנרגיה ניתן לביטוי כ:

הביטוי הנ”ל ניתן גם להצגה במונחים של מקדם מעבר חום כללי:

כאשר אם מוגדר במונחים של השטח הפנימי, , אז:

דוגמה: בידוד צינורות דקים

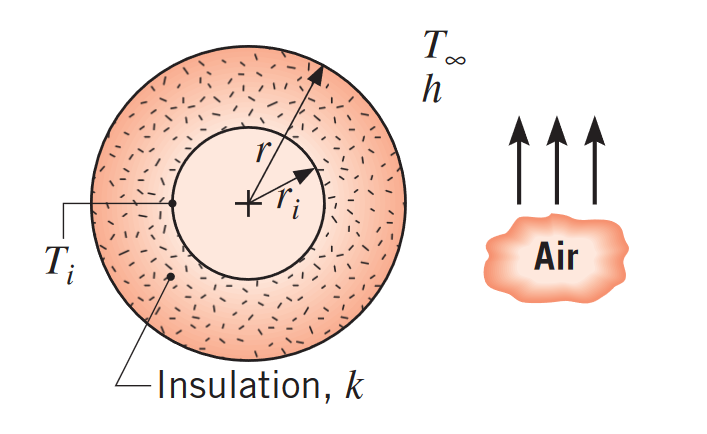
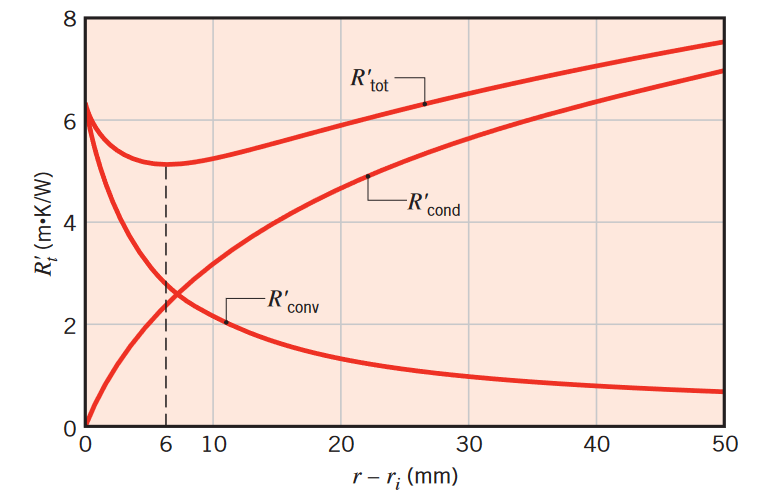
כאשר אנו רוצים לבודד צינור דק מהסביבה, ישנם שני אפקטים מנוגדים שפועלים אם מגדילים את עובי המבודד. מצד אחד, הגדלת העובי מעלה את התנגדות ההולכה. אבל, הגדלת העובי, שטח הפנים החיצוני של הצינור גדל, ובכך מקטין את התנגדות ההסעה. נרצה לדעת מהו העובי האופטימלי כדי לקבל איבוד חום מינימלי מהצינור. פתור את בעיה זאת לפי המערכת הבאה:

צינור דק ברדיוס מזרים בתוכו נוזל קירור בטמפרטורה שנמוכה יותר מהטמפרטורה בסביבה, שהיא . האם יש עובי אופטימלי עבור השימוש של הבידוד לצינור?

פתרון:
הנחות:

1. מצב מתמיד.
2. מעבר חום חד-ממדי בכיוון הרדיאלי.
3. התנגדות תרמית זניחה לקיר הצינור.
4. תכונות אחידות למבודד.
5. קרינה זניחה בין המשטח החיצוני של המבודד והסביבה.

ההתנגדות למעבר חום בין נוזל הקירור והאוויר נשלט ע”י ההולכה במבודד וההסעה באוויר. לכן המעגל התרמי הוא:

לכן, סך ההתנגדות ליחידת אורך של הצינור היא:

כך שקצב המעבר חום ליחידת אורך של הצינור הוא:

עובי בידוד אופטימלי הוא העובי עבורו מינימלי - כלומר מקסימלי. לכן נדרוש ש- :

כדי לוודא שגודל זה הוא אכן מקסימום, ולא סתם נקודת קיצון כללית, נבדוק את ערך הנגזרת השנייה של עבור :

ב- :

מאחר וגודל זה תמיד חיובי, נסיק ש- הוא העובי עבורו סך ההתנגדות היא מינימלית, לא מקסימלית. לכן, עובי בידוד אופטימלי לא קיים.
מתוצאה זו יותר הגיני לחשוב על הגודל כעובי בידוד קריטי:

הבידוד התרמי כתלות ב- תחת נתונים מסוימים. (Bergman & Lavine, 2017).

קליפה כדורית

נביט כעת בקליפה כדורית:

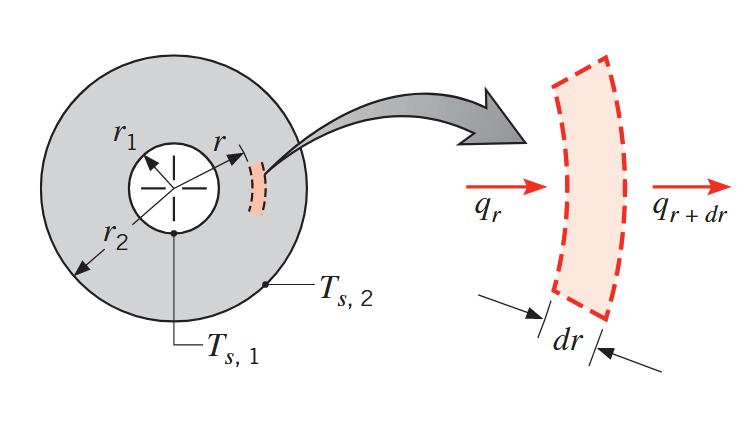
.הולכה בקליפה כדורית. (Bergman & Lavine, 2017).

עבור הנפח בקרה הדיפרנציאלי באיור, משימור אנרגיה אנו יודעים ש- עבור מצב מתמיד, תנאים חד-ממדיים ללא יצירת חום. חוק פורייה המתאים:

כאשר הוא השטח הניצב לכיוון מעבר החום.
בהנחה ו- קבוע ולא תלוי ב-, האינטגרציה של המשוואה לעיל תניב:

בהנחה ו- קבוע, נקבל:

נזכור שההתנגדות התרמית מוגדרת כהפרש הטמפרטורות חלקי הקצב מעבר חום, ולכן:

הולכה עם ייצור חום פנימי

נרצה כעת לבחון כיצד ייצור חום פנימי עלול להשפיע על פתרון משוואת חום. מקרה נפוץ של ייצור חום פנימי הוא המרה של אנרגיה חשמלית לאנרגיה תרמית בתווך מוליך חשמלי כלשהו. הקצב בו האנרגיה נוצרת ע”י זרם דרך תווך עם התנגדות חשמלית נתון לפי הספק חום מהתנגדות:

אם ייצור חום זה () מתרחש באופן אחיד בתווך שנפחו , קצב הייצור הנפחי הוא:

לוח פשוט

נביט בלוח פשוט עם ייצור חום פנימי אחיד ומשטחים בטמפרטורות ו-:

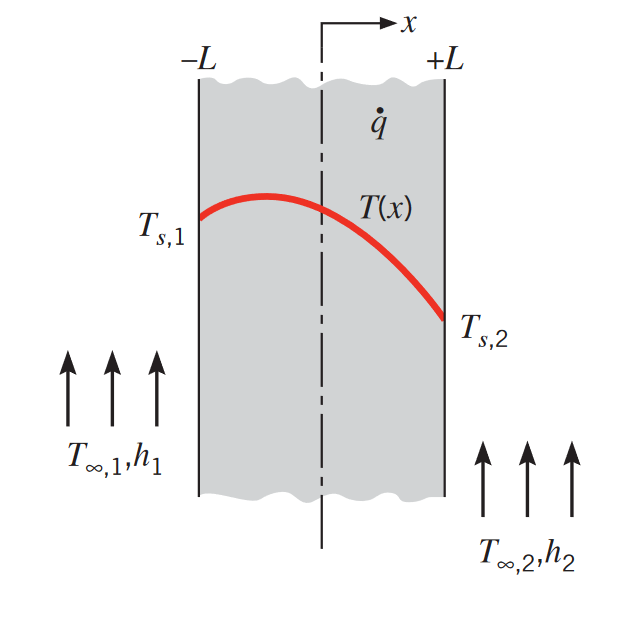
הולכה בלוח מישורי עם ייצור חום אחיד, עם תנאי שפה לא סימטריים. (Bergman & Lavine, 2017).

עבור הולכת חום אחידה, למשוואת החום יש את הצורה הבאה:

הפתרון הכללי למשוואה זו הוא:

כאשר ו- הם קבועי האינטגרציה. עבור תנאי השפה הנתונים -

הקבועים ניתנים לקביעה, והם מהצורה:

במקרה זה הפילוג טמפרטורה הוא:

מצורת פתרון זו, ומהאיור למעלה, ניתן ישירות לקשר בין פילוג חום זה לפילוג המהירויות בזרימה צמיגה - הם מתוארים ע”י אותם המשוואות המתמטיות.

בעזרת פילוג המהירויות נוכל למצוא את שטף מעבר החום בכל נקודה בעזרת חוק פורייה. נשים לב הפעם שעם ייצור חום, השטף חום כעת תלוי ב-.
כאשר הטמפרטורות בשני המשטחים שווים (), פילוג הטמפרטורות הופך להיות סימטרי:

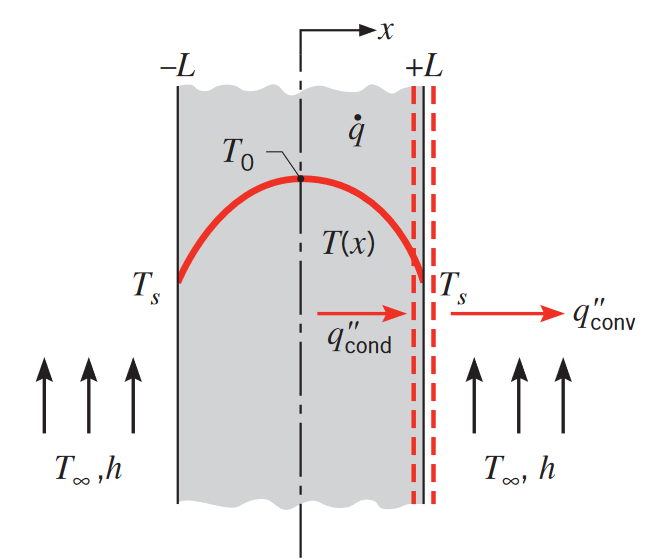
הולכה בלוח מישורי עם ייצור חום אחיד, עם תנאי שפה סימטריים. (Bergman & Lavine, 2017).

הטמפרטורה המקסימלית תהיה:

ופילוג הטמפרטורות יהיה מהצורה:

נשים לב שבמישור הסימטריה, גרדיאנט הטמפרטורה הוא אפסי (). לכן, אין מעבר חום דרך מישור זה, כך שאפשר להתייחס אליו כתנאי שפה אדיאבטי. לכן, הפתרון עבור הבעיה הסימטרית תקף גם ללוחות שמבודדים לחלוטין מצד אחד, ונמצאים בטמפרטורה קבועה מצד שני:

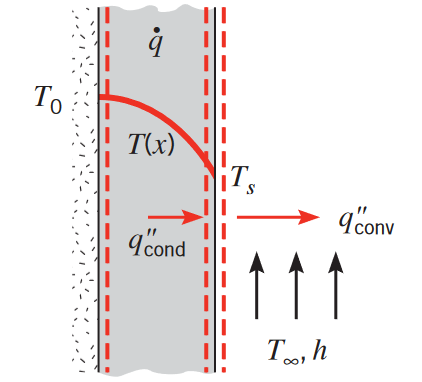
הולכה בלוח מישורי עם ייצור חום אחיד, עם תנאי שפה אדיאבטי. (Bergman & Lavine, 2017).

מערכות רדיאליות

נדון כעת במקרה של ייצור חום פנימי במערכות רדיאליות:

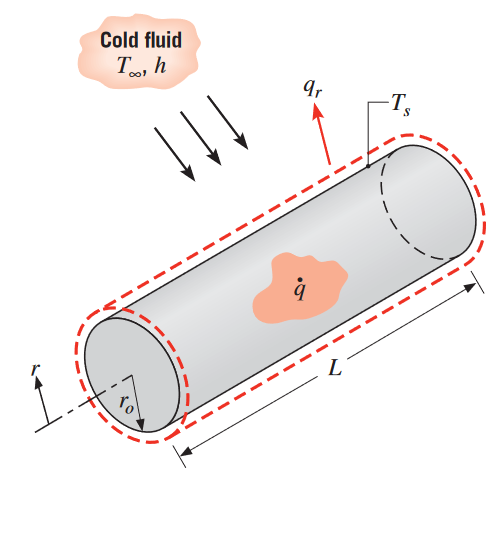
הולכה בגליל מוצק עם ייצור חום פנימי קבוע. (Bergman & Lavine, 2017).

נתחיל ממשוואת החום בכיוון הרדיאלי:

לאחר אינטגרציה נקבל:

כדי למצוא את נשים לב שיש לנו את תנאי השפה:

תנאי זה מגיע מסימטריות הבעיה - בגליל, בציר הסימטריה שלו, גרדיאנט הטמפרטורה שלו חייב להיות אפס, כפי שראינו גם עבור לוח פשוט. מהצבת תנאי שפה זה נקבל ש- , כך שנישאר עם:

לאחר עוד אינטגרציה נקבל:

מהצבת תנאי השפה , נמצא כי:

מעבר חום ממשטחים מורחבים

משטחים מורחבים (extended surfaces) במובנים של מעבר חום הוא ביטוי למקרה מיוחד הנוגע להולכה בגוף, ומעבר חום ע”י הסעה (או קרינה) מהגבולות של הגוף. עד עכשיו עסקנו במעברי חום מהגבולות של הגוף שבאותו הכיוון של ההולכה בתוך הגוף. לעומת זאת, במשטחים מורחבים, הכיוון של מעבר החום מהגבולות ניצב לכיוון הראשי של המעבר חום במוצק.
נביט במשטח המורחב הבא המחברת בין שתי לוחות בטמפרטורות שונות, שדרכו עבור זרם:

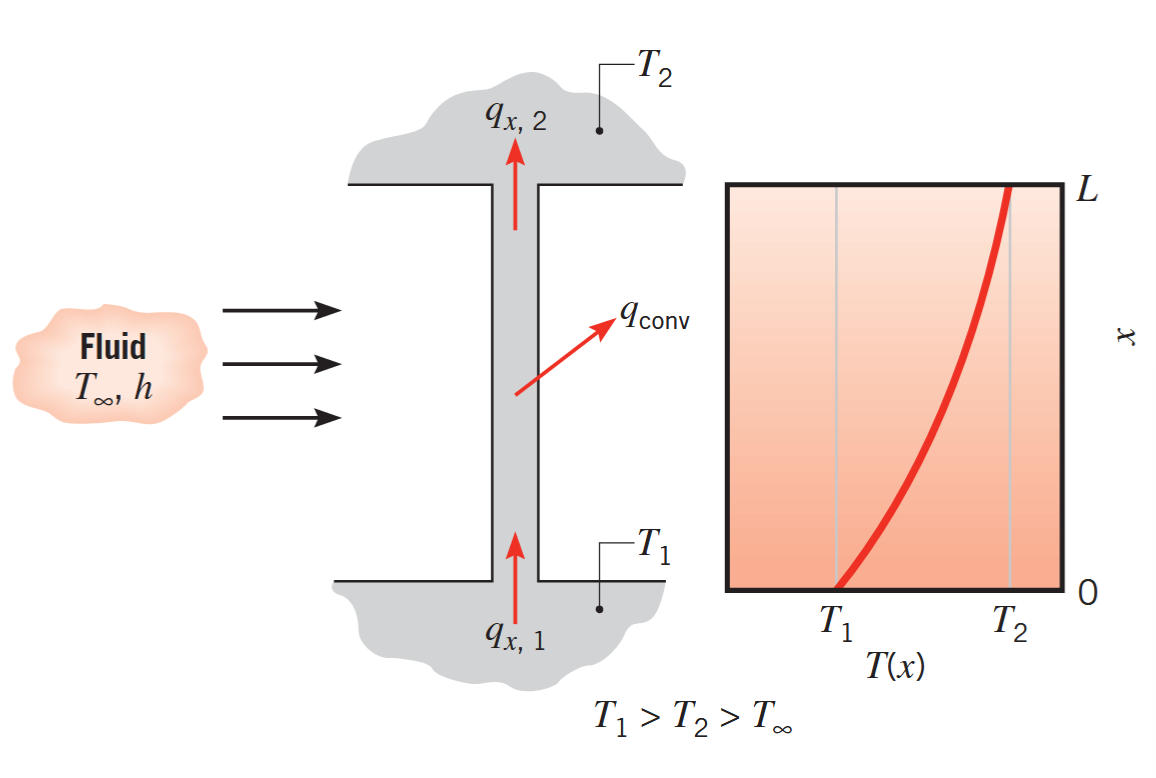
הולכה והסעה במשטח מורחב. (Bergman & Lavine, 2017).

כאשר , גרדיאנט הטמפרטורה בכיוון נשלט ע”י ההולכה בכיוון . אבל, כאשר , יש מעבר חום בהסעה אל הזורם, מה שיוצר , כך שגודל גרדיאנט הטמפרטורה יורד ככל שמתקדמים לאורך .

השימוש הנפוץ ביותר של משטח מורחב הוא כדי להגביר את מעבר החום בין מוצק לזורם. למשטח מורחב כזה קוראים צלע (fin).

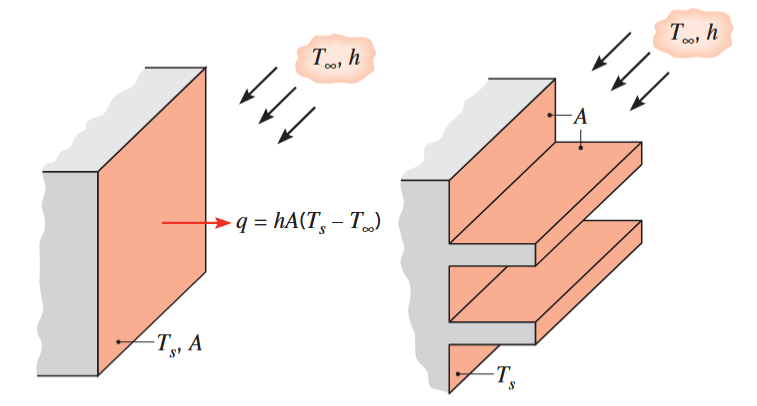
שימוש בצלעות לשיפור המעבר חום. (Bergman & Lavine, 2017).

ניתוח הולכה בצלעות

כדי למצוא את ההולכה בצלעות, אנו ראשית צריכים למצוא את פילוג הטמפרטורה לאורך הצלע. נתחיל ממאזן אנרגיה על אלמנט דיפרנציאלי כפי שמתואר באויר הבא:

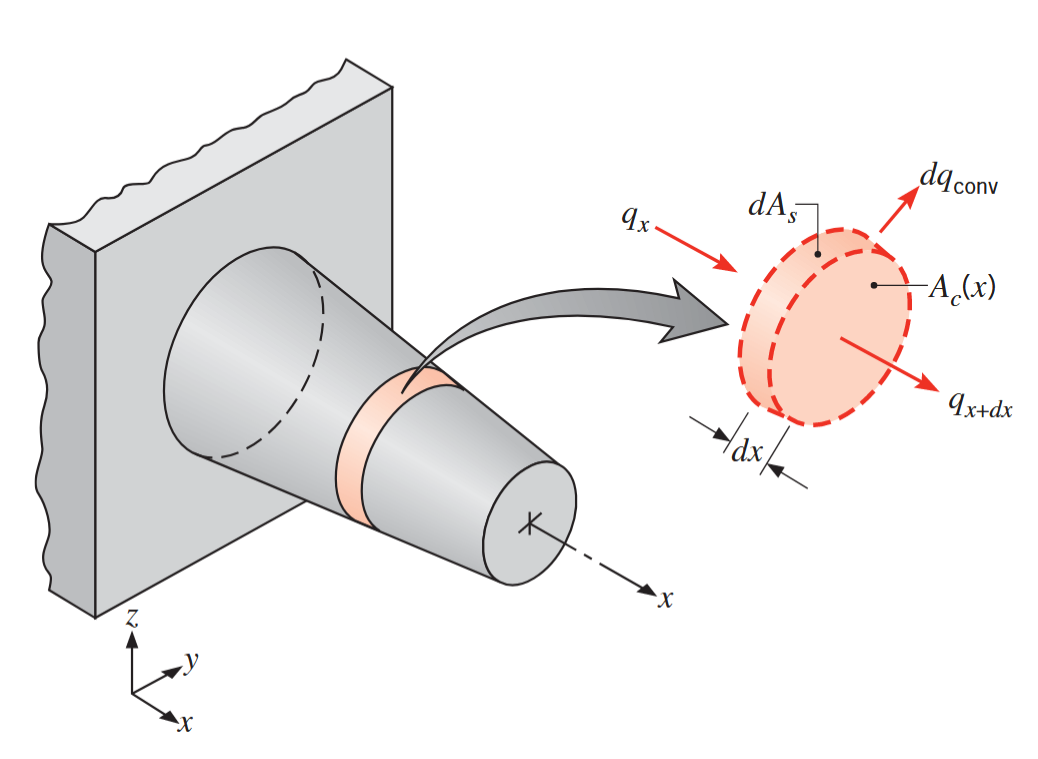
מאזן אנרגיה על צלע. (Bergman & Lavine, 2017).

נניח שהבעיה חד ממדית, בכיוון , למרות שההולכה בצלע היא למעשה דו-ממדית. הקצב בו האנרגיה מולכת אל הזורם בכל נקודה על משטח הצלע חייב להיות מאוזן ע”י סך הקצב בו האנרגיה מגיעה לנקודה זו ע”י הולכה בכיוונים ו-. אבל, אנו יודעים שהצלע היא דקה, והשינוי טמפרטורה בכיוונים ו- הם זניחים לעומת השוני בטמפרטורות בין הצלע והסביבה. לכן, אנו יכולים להניח שהטמפרטורה אחידה לאורך עובי הצלע, כך שלמעשה היא אך ורק פונקציה של (ולא גם של ו-).
נניח גם שאנו במצב מתמיד, ההולכה התרמית היא קבועה, הקרינה זניחה, אין ייצור חום, והמקדם הסעה אחיד לאורך המשטח.

לפי החוק הראשון של התרמודינמיקה:

מחוק פורייה אנו יודעים ש:

כאשר הוא שטח השטח חתך, שעלול להשתנות עם . מאחר והולכה ב- ניתנת לביטוי כ:

נסיק כי:

המעבר חום בהסעה ניתן לביטוי כ:

כאשר הוא השטח של האלמנט הדיפרנציאלי ו- הוא ההיקף שלו. הצבה של ביטויים אלו בחזרה בחוק ראשון תניב:

או:

צלעות עם שטח חתך אחיד

כדי לפתור את משוואת החום הנ”ל אנו צריכים להיות יותר ספציפיים לגבי הגאומטרייה. במקרה הפשוט של שטח חתך אחיד:

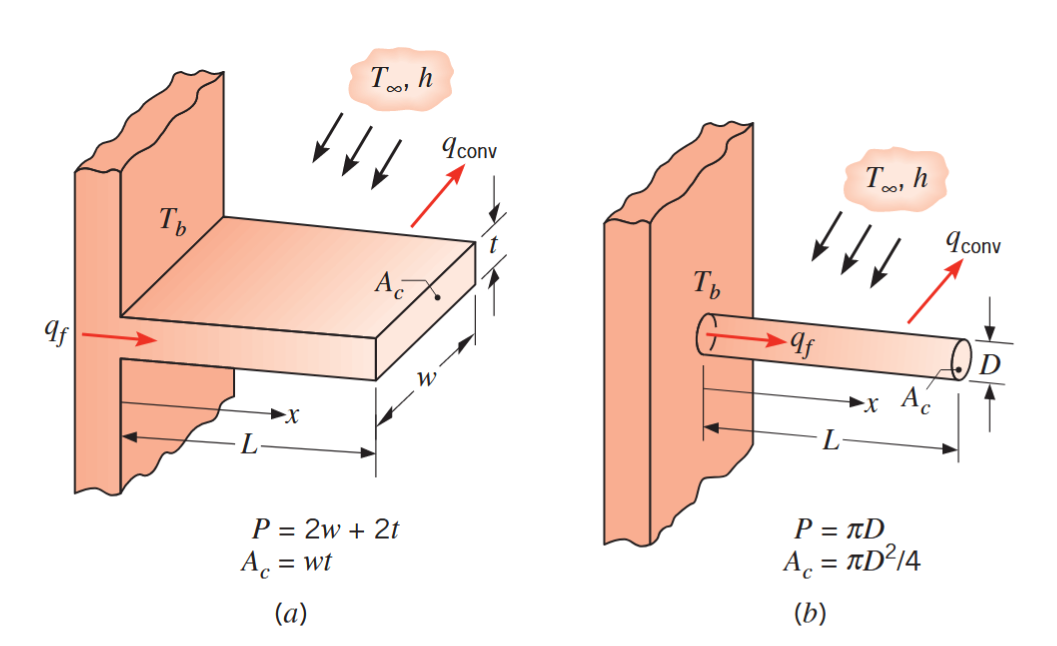
צלע עם שטח חתך מלבני. (Bergman & Lavine, 2017).

כל אחת מהצלעות מחוברת לבסיס עם טמפרטורה , ונמצאת בזורם בעל טמפרטורה . עבור הצלעות הנתונות, ו- קבועים, כך ש- , ולכן משוואת החום הופכת לצורה:

כדי לפשט את המשוואה הזו, נוח להגדיר משתנה חדש הנקרא טמפרטורה עודפת :

כיוון ש- קבוע, מתקיים , ואז משוואת החום היא פשוט:

כאשר:

משוואת החום שקיבלנו היא לינארית, הומוגנית, מד”ר מסדר שני עם מקדמים קבועים. הפתרון שלה הוא פשוט:

את הקבועים ו- נוכל כמובן למצוא מהתנאי שפה. בבסיס, התנאי שפה הוא:

עבור התנאי שפה השני, נוח לרוב למצוא את התנאי בקצה (). אם התנאי שפה הוא הסעה בקצה:

משני תנאי שפה אלו אנו מקבלים:

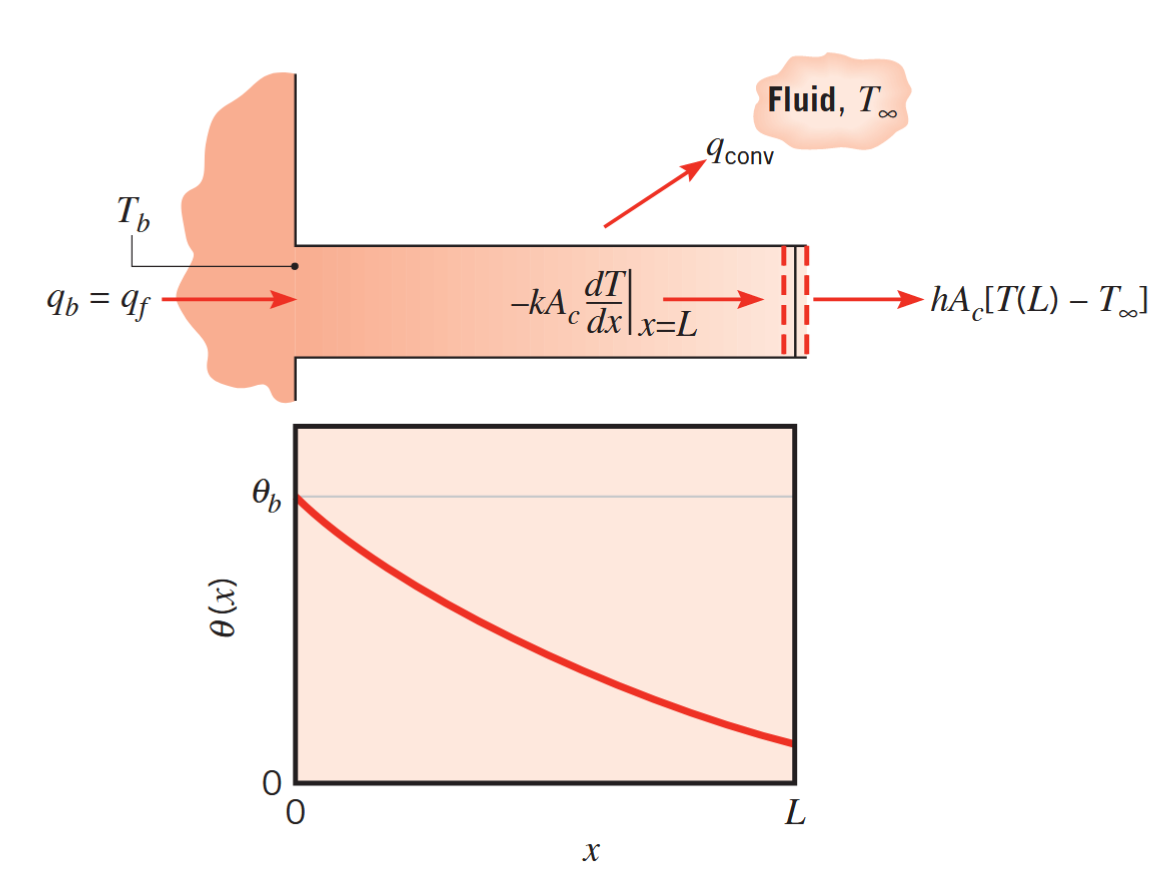
הולכה בצלע עם שטח חתך אחיד ותנאי שפה של הסעה. (Bergman & Lavine, 2017).

לרוב נרצה למצוא את סך המעבר חום מכל הצלע. מהאיור הנ”ל, ניתן לראות שנוכל לעשות זאת בשני דרכים:

1. חוק פורייה בבסיס הצלע: בעזרת הביטוי שמוצאים עבור , ניתן להציב ולקבל את . במקרה של הסעה בקצה:
2. כאלטרנטיבה, מחוק ראשון אנו יודעים שהקצב בו חום מועבר בהסעה מהצלע חייב להיות שווה לקצב בו הוא מולך דרך בסיס הצלע. לכן: כאשר הוא סך שטח הפנים (כולל הקצה) של הצלע.

טבלה 3.4 מסכמת את המקרים השונים.

פרמטרי ביצועי הצלע

ראינו צלעות משמשות לשיפור המעבר חום ממשטח ע”י הגדלת שטח הפנים שלו. אבל, לצלע עצמה יש התנגדות תרמית. לכן, אין הבטחה שקצב המעבר חום יגדל משימוש הצלעות.

יעילות צלע

הגדרה: יעילות צלע

יעילות צלע, מוגדרת, עבור משטח בעל טמפרטורת בסיס קבועה, כהיחס בין קצב המעבר חום של הצלע לקצב המעבר חום ללא הצלע:

כאשר הוא שטח החתך של הצלע בבסיס. לרוב, השימוש בצלעות הוא כאשר .

למשל, בהסתמך על טבלה 3.4, במידה ומדובר בצלע אינסופית, אנו יודעים ש- . לכן היעילות של צלע כזאת היא:

נסיק שיעילות הצלע משתפרת משמעותית עם הבחירה של חומר בעל הולכה תרמית גבוהה. נקודה מעניינת היא שסגסוגות אלומיניום הם הבחירה הנפוצה לצלעות היום, למרות שלסגסוגות נחושת יש הולכה תרמית גבוהה יותר - האלומיניום זול וקל יותר.
יעילות הצלעות גם משתפרת ע”י הגברת היחס בין ההיקף לשטח החתך. מסיבה זאת, נעדיף צלעות דקות עם מרווחים קטנים ביניהן, עם התנאי שהמרווח לא יקטן מערך מסוים בו הזרימה בין הצלעות תיפגע משמעותית, מה שינמיך את מקדם ההסעה .

התנגדות צלע

ניתן למדוד את ביצועי הצלע גם במובנים של התנגדות תרמית.

הגדרה: התנגדות צלע

התנגדות צלע היא היחס בין הפרשי הטמפרטורות בין הבסיס לזורם לקצב מעבר חום:

הגדרה זו מאוד שימושית אם נרצה לתאר את הצלע במעגל תרמי.
בנוסף, ניזכר גם שההתנגדות תרמית להסעה בבסיס אם הוא היה חשוף היא:

ולכן נוכל לרשום את היעילות התרמית גם כהיחס:

לכן, נוכל לחשוב על יעילות הצלע גם כיחס בין התנגדויות תרמיות, ושכדי להגדיל את עלינו להקטין את התנגדות הצלע להסעה/הולכה. אם הצלע מיועדת להגברת מעבר חום, אסור שההתנגדות שלה תהיה גבוהה יותר מההתנגדות של הבסיס החשוף.

נצילות צלע

הגדרה: נצילות צלע

נצילות צלע מוגדרת כהיחס בין קצב מעבר החום האמיתי, , לקצב מעבר החום המקסימלי האפשרי. קצב מעבר החום המקסימלי מהצלע מתרחש אם כל הצלע הייתה בטמפרטורת הבסיס :

כאשר הוא שטח הפנים של הצלע שבהסעה.

עבור צלע ישרה עם שטח חתך אחיד וקצה אדיאבטי, מטבלה 3.4, קצב מעבר החום הוא

ולכן הנצילות:

תוצאה זו אומרת לנו ש- שואף לערכים המקסימליים והמינימליים שלו ו-, בהתאמה, כאשר שואף ל- ו-, בהתאמה. כלומר, אם הצלע ארוכה מדי, הנצילות קטנה אבל אם היא קצרה מדי הנצילות מאוד גבוהה אבל לא פינינו הרבה חום.

נוכל להיעזר בנצילות צלע כדי למצוא את התנגדות הצלע:

תיקונים לאורכי צלעות

הביטוי למעבר חום שקיבלנו עבור תנאי שפה הסעה די מסובכת:

אבל, ניתן להראות שאם נשתמש במקום זאת בביטוי למעבר חום עם תנאי שפה אדיאבטי בקצה

אבל עם תיקון לאורך צלע מהצורה לצלע מרובעת או לצלע עגולה, נקבל קירוב מאוד טוב למעבר חום האמיתי. קירוב זה מבוסס על ההנחה שהמעבר חום של צלע עם קצה בהסעה שקול למעבר של צלע קצת יותר ארוכה עם קצה אדיאבטי. לכן, עם הסעה בקצה, הקצב מעבר חום ניתן לקירוב כ

והנצילות כ:

השגיאה בקירוב זה זניחה אם:

הנצילויות והתיקונים לצלעות שונות נתונים בטבלה 3.5.

צלעות עם שטח חתך משתנה

הביטוי השני במשוואה (IH3.66) לא יכול להתבטל במקרה של צלעות עם שטח חתך משתנה, והפתרונות כבר לא בצורה של אקספוננט או פונקציה היפרבולית. מקרה מיוחד הוא המקרה של צלע טבעתית:

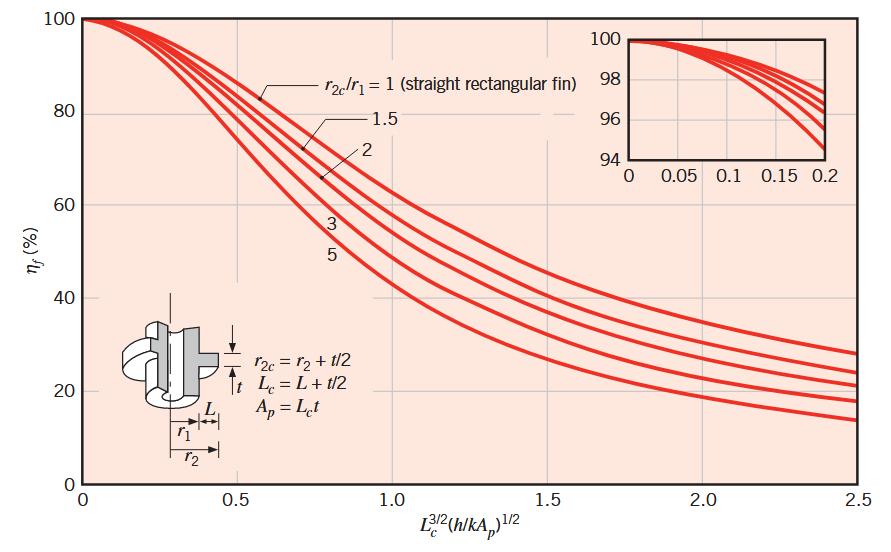
נצילות של צלעות טבעתיות עם פרופיל מלבני. (Bergman & Lavine, 2017).

למרות שעובי הצלע הוא אחיד ( לא תלוי ב-), שטח החתך, , משתנה עם . אם נמשיך ממשוואה (IH3.66) עם החלפת משתנים מ- ל-, ונבטא את שטח הפנים כ- , המשוואה תהפוך להיות מהצורה:

כאשר נבחר ו- :

למשוואה זו יש פתרון אנליטי, אבל לא נעסוק בו במסגרת הקורס. אפילו הפתרון שלו, שמופיע בטבלה 3.5 (עבור annular fin), הוא מעיק לחישוב, אז נסתפק בקירובים לפי הגרף לעיל.
אם מדובר בצלעות משולשות או פרבוליות, אז יש להשתמש בגרף הבא:

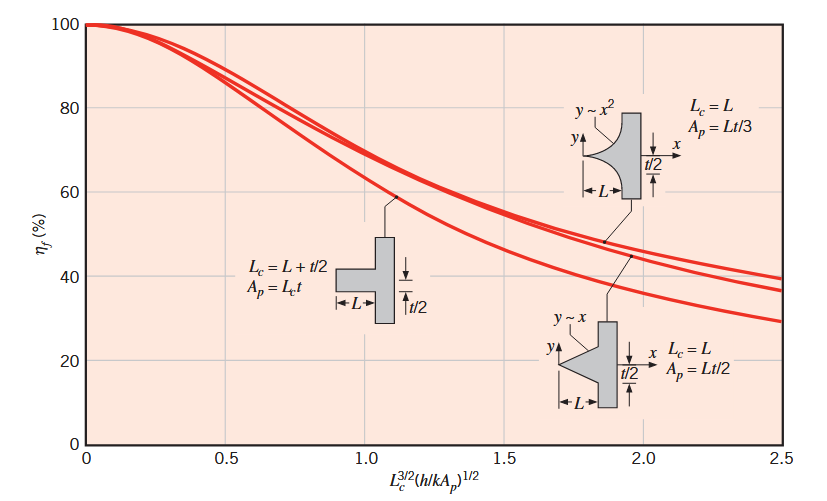
נצילות כוללת

לעומת נצילות צלע שמאפיינת את צלע אחת, הנצילות הכוללת מאפיינת מערך של צלעות והבסיס אליו הם מחוברים.

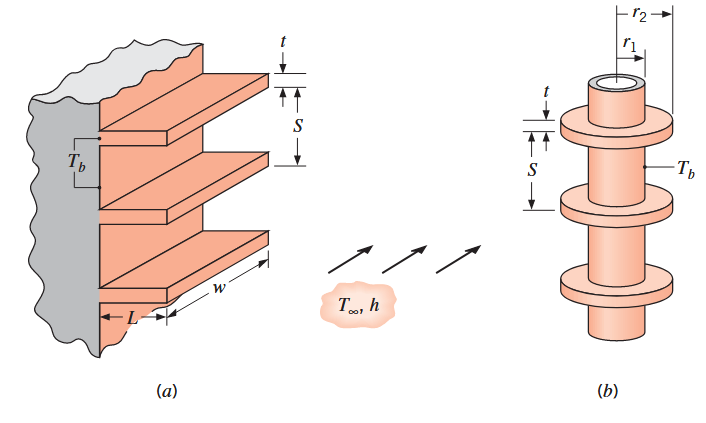
מערך צלעות. (a) צלעות מרובעות. (b) צלעות טבעתיות. (Bergman & Lavine, 2017).

הגדרה:

הנצילות הכוללת של מערך צלעות מוגדרת כ

כאשר הוא סך קצב מעבר החום מהשטח פנים של כל הצלעות והבסיס החשוף שלהם.

אם ישנם צלעות במערך, כל אחד עם שטח פנים , והשטח של הבסיס החשוף הוא , אז סך שטח הפנים הוא:

קצב המעבר חום המקסימלי מתקבל אם כלל שטח הפנים בטמפרטורה .
סך הקצב מעבר חום בהסעה מהצלעות ומהבסיסים החשופים שלהם ניתן לביטוי כ

כאשר אנו מניחים שמקדם ההסעה זהה עבור הצלעות והבסיסים שלהם, וש- הוא הנצילות של צלע אחת. לכן:

נסיק כי נוכל לרשום את הנצילות הכוללת גם כ:

מההגדרה של התנגדות תרמית, נוכל גם לפתח ביטוי להתנגדות התרמית של מערכת הצלעות:

לאחר פיתוחים, ניתן גם להראות:

אם הצלעות יוצרו בנפרד מהמשטח אליו הם מחוברים, יש התנגדות מגע שעלולה להשפיע (לרעה) על ביצועי הצלעות. במקרה זה:

כאשר:

תרגילים

שאלה 1

על צידו האחד של קיר בעל שטח , עובי ומוליכות תרמית מותקן לוח חשמלי דק אשר מבודד מצידו האחד וצמוד לקיר בצידו השני. הלוח פולט חום בהספק .

סכמת הבעיה

בין הלוח החשמלי לקיר ישנה התנגדות מגע . הצד השני של הקיר חשוף לסביבת אוויר בטמפרטורה ומקדם מעבר החום בהסעה בין הקיר לאוויר הוא .

סעיף א’

מהי טמפרטורת הלוח החשמלי ?

פתרון:

מעגל תרמי שקול

לכן ההתנגדות התרמית הכוללת:

נציב נתונים ונקבל:

לכן, מהגדרת ההתנגדות התרמית:

נציב נתונים:

סעיף ב’

מהי טמפרטורת הלוח לאחר התחשבות בקרינה לסביבה של ואמיסיביות קיר של ?

פתרון:
נוכל להתייחס לקרינה כהתנגדות תרמית מחוברת במקביל:

מעגל תרמי שקול

כעת ההתנגדות השקולה היא מהצורה:

כאשר הוא ההתנגדות השקולה של החיבור במקביל:

מהתנגדות לקרינה:

אנחנו לא יודעים מהו , אז נמצא קירוב התחלתי עבורו (נזניח את הקרינה כדי לחשב אותו):

נציב נתונים:

נוכל להציב הכל בחזרה במקומות המתאימים כדי להסיק כי:

לכן טמפרטורת הלוח היא:

סעיף ג’

מה תהיה טמפרטורת הלוח החשמלי אילו לא היה בידוד והלוח היה חשוף גם הוא לסביבה?

פתרון:
אם הלוח גם היה חשוף לסביבה, במעגל התרמי השקול נוסיף עוד חיבור לסביבה - מצד שמאל. מאחר וכבר יש לנו חיבור מצד ימין ל-, נוכל לאחד בין שניהם כך שלמעשה מתקבל לנו החיבור במקביל הבא:

סכמת הבעיה

לכן ההתנגדות הכוללת החדשה היא:

כך שנוכל לחשב את :

שאלה 2

שכבה של דלק גרעיני בעובי ומוליכות תרמית מכוסה בפלדה בעובי ומוליכות תרמית משני צדדיה, ומייצרת חום בקצב . בצד אחד יש סביבה בטמפרטורה ומקדם מעבר חום בהסעה . מצד שני הפלדה מבודדת. הניחו מעבר חום חד-מדדי בכיוון .

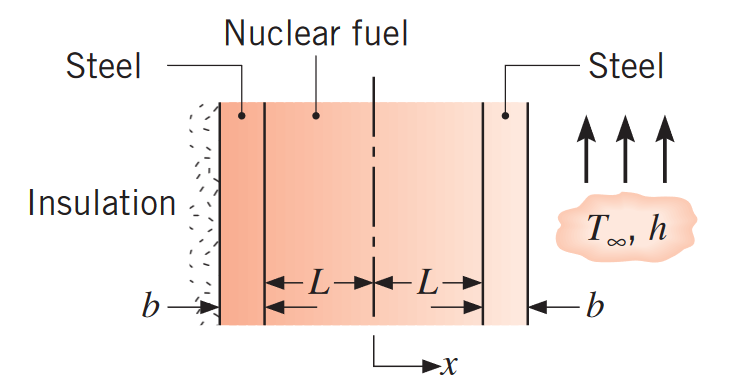
סכמת הבעיה. (Bergman & Lavine, 2017).

סעיף א’

מצאו ביטוי להתפלגות הטמפרטורה בשכבת הדלק.

פתרון:

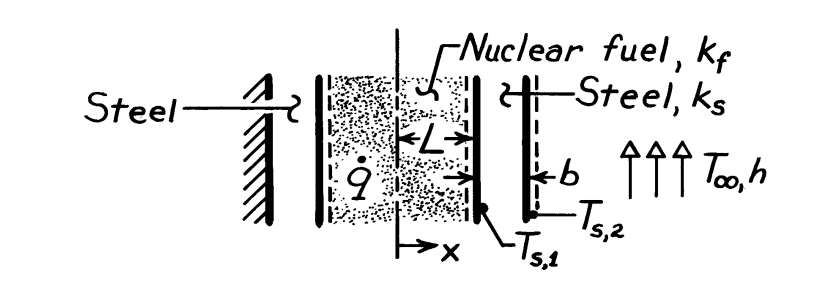
סכמת הבעיה

מהולכה עם ייצור חום פנימי, משוואת החום במצב מתמיד היא מהצורה:

מאחר ויש בידוד ב- , נסיק ששטף החום ב- הוא אפס (נוכל לבחור את האזור ליד הקיר כנפח בקרה, ולהסיק מחוק ראשון ש- ). לכן:

התנאי שפה השני הוא ב- בו הטמפרטורה היא . נוכל למצוא את טמפרטורה זו מחוק ראשון - . ליחידת שטח זה אומר ש (לפי חוק פורייה וחוק הקירור של ניוטון):

נקבל ש- , ולכן:

כעת נוכל למצוא את הקבוע השני, :

לכן פילוג הטמפרטורה הוא:

סעיף ב’

ושרטטו באופן איכותי את פילוג הטמפרטורה מהבידוד לסביבה.

פתרון:

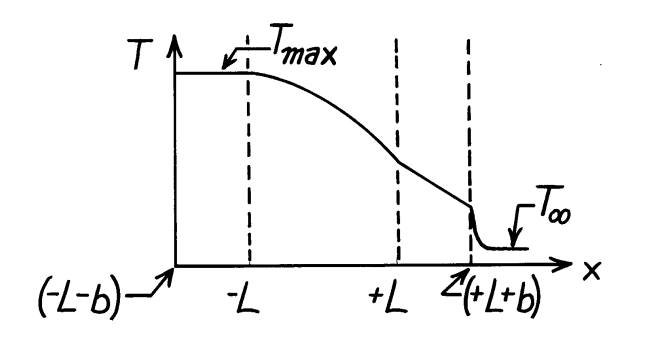
פילוג הטמפרטורה מהבידוד לסביבה.

שאלה 3

מייצרים חלק קוני מאלומיניום. יש לחלק חתך עגול בעל קוטר משתנה , כאשר . הפאה הקטנה נמצאת במיקום והפאה הגדולה נמצאת במיקום במערכת קואורדינטות בה .

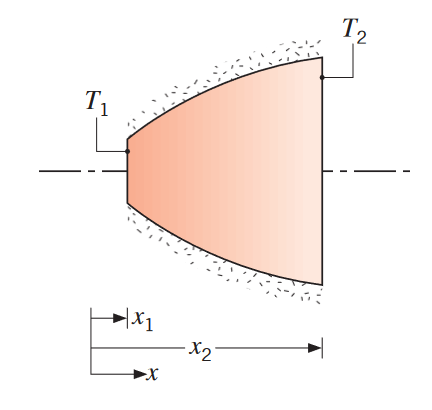
סכמת הבעיה. (Bergman & Lavine, 2017).

נמדדו הטמפרטורות בפאות והשפה המעוגלת מבודדת היטב. מוליכות תרמית של אלומיניום היא . יש לחשב את קצב מעבר החום במצב מתמיד ולמצוא את פילוג הטמפרטורה בגוף.

פתרון:
הנחות:

1. מצב מתמיד
2. הולכה חד-ממדית
3. אין ייצור חום פנימי
4. תכונות אחידות

בהתבסס על ההנחות, לפי חוק פורייה, ההספק דרך שטח חתך במיקום הוא:

נעביר אגפים כי אנו רוצים למצוא ביטוי ל-:

בפרט, עבור :

נעביר אגפים כדי לקבל ביטוי עבור :

נציב בביטוי עבור הפילוג טמפרטורה:

שאלה 4

מוט מתכת בעל ממדים ו- ומוליכות תרמית מותקן בניצב לקיר בעל טמפרטורה אחידה .

סכמת הבעיה.

המוט חשוף לזרימת אוויר ונמצא במצב מתמיד.

סעיף א’

האם מתקיימים התנאים לקירוב של צלע אין-סופית?

פתרון:
אנו מניחים שהצלע בקירוב אינסופית כאשר , שזה אומר . במקרה שלנו:

ולכן נוכל להניח כי הצלע אינסופית.

סעיף ב’

חשבו את קצב פינוי החום ע”י המוט מהקיר.

פתרון:
מטבלה 3.4, עבור צלע אינסופית (מקרה D):

נקבל כי:

סעיף ג’

חשבו את נצילות ויעילות המוט.

פתרון:
מהגדרת הנצילות:

נקבל כי:

מהגדרת היעילות:

ולכן:

סעיף ד’

כעת, המוט מוכנס לתוך בידוד, כאשר חצי מאורכו חשוף לזרימת אוויר , ובחציו של המוט הנמצא בבידוד נוצר חום בקצב של . הניחו מעבר חום במצב מתמיד.

סכמת הבעיה.

חשבו את הטמפרטורה באמצע המוט.

פתרון:
ניעזר בביטוי לקצב מעבר החום בבסיס הצלע :

מכיוון שהצלע פועלת במצב מתמיד, ניתן לראות שקצב מעבר החום דרך בסיס הצלע הוא בדיוק אותו החום שנוצר בחלק הפנימי של המוט:

ולכן:

נציב נתונים ונקבל:

סעיף ה’

חשבו את הטמפרטורה של קצה המוט.

פתרון:
נמצא את פילוג הטמפרטורה בחלק הפנימי של המוט, בהנחה של מעבר חום דו-ממדי ומצב מתמיד. משוואת החום כולל ייצור חום פנימי:

נפתור ע”י אינטגרציה פעמיים:

תנאי השפה הם בידוד בקצה השמאלי וטמפרטורה ידועה בקצה הימני :

ולכן פילוג הטמפרטורה:

בפרט, בקצה המוט:

נציב נתונים וגדלים ידועים ונקבל:

סעיף ו’

שרטטו את פילוג הטמפרטורה בתוך המוט.

פתרון:
נותר לנו למצוא את פילוג הטמפרטורה בחלק החיצוני של המוט, שלפי טבלה 3.4 הוא:

נקבל גרף מהצורה:

פילוג הטמפרטורה בתוך המוט.

→ קודם: HTF1_001הבא: HTF1_003 ←