HTF1_009 קרינה

→ קודם: HTF1_008

מבוא

כל גוף שיש לו טמפרטורה שונה מ- פולט קרינה. הקרינה נובעת כתוצאה מהתנועה הרנדומלית של החלקיקים, ותנועה זו גורמת להיווצרות גלים אלקטרומגנטיים, שלעומת הולכה והסעה, לא צריכים תווך מסוים כדי שיתקדמו במרחב.

בהינתן מוצר מסוים שבהתחלה חם יותר מהסביבה , אבל סביבו קיים ריק.

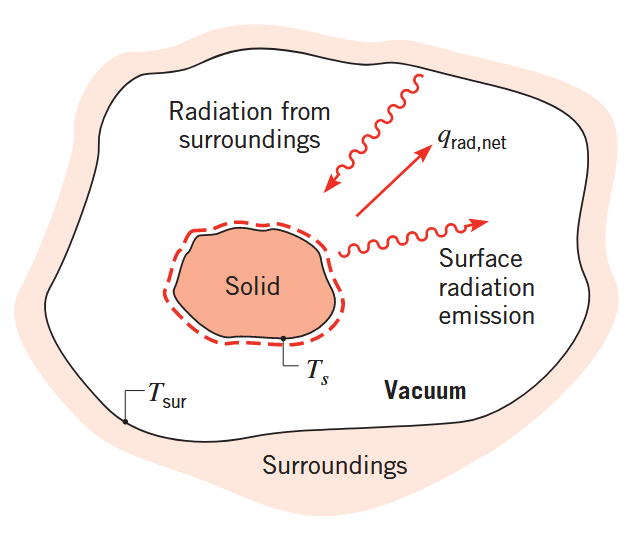
קירור בקרינה של מוצק. (Bergman & Lavine, 2017).

קיום הריק מונע מכך שהמוצק יתקרר ע”י הסעה או הולכה דרך השפה שלו. אבל, מתוך אינטואיציה, אנו יודעים שהמוצק יתקרר ולבסוף יגיע לשיווי משקל תרמי עם סביבתו. קירור זה הוא כתוצאה ישירה מה-פליטה של קרינה תרמית ממשטחו. באותו האופן, המשטח גם יקלוט קרינה מסביבתו. אבל, אם , סך קצב מעבר החום בקרינה הוא מ-המשטח, והמשטח יתקרר עד ש- יגיע ל-.

כל סוגי החומרים פולטים קרינה. לגזים ומוצקים שקופים למחצה, כמו זכוכית וגבישי מלח בטמפרטורות גבוהות, הפליטה היא תופעה נפחית, כפי שמוצג איור הבא. כלומר, הקרינה נפלטת מכל אלמנט נפחי בחומר:

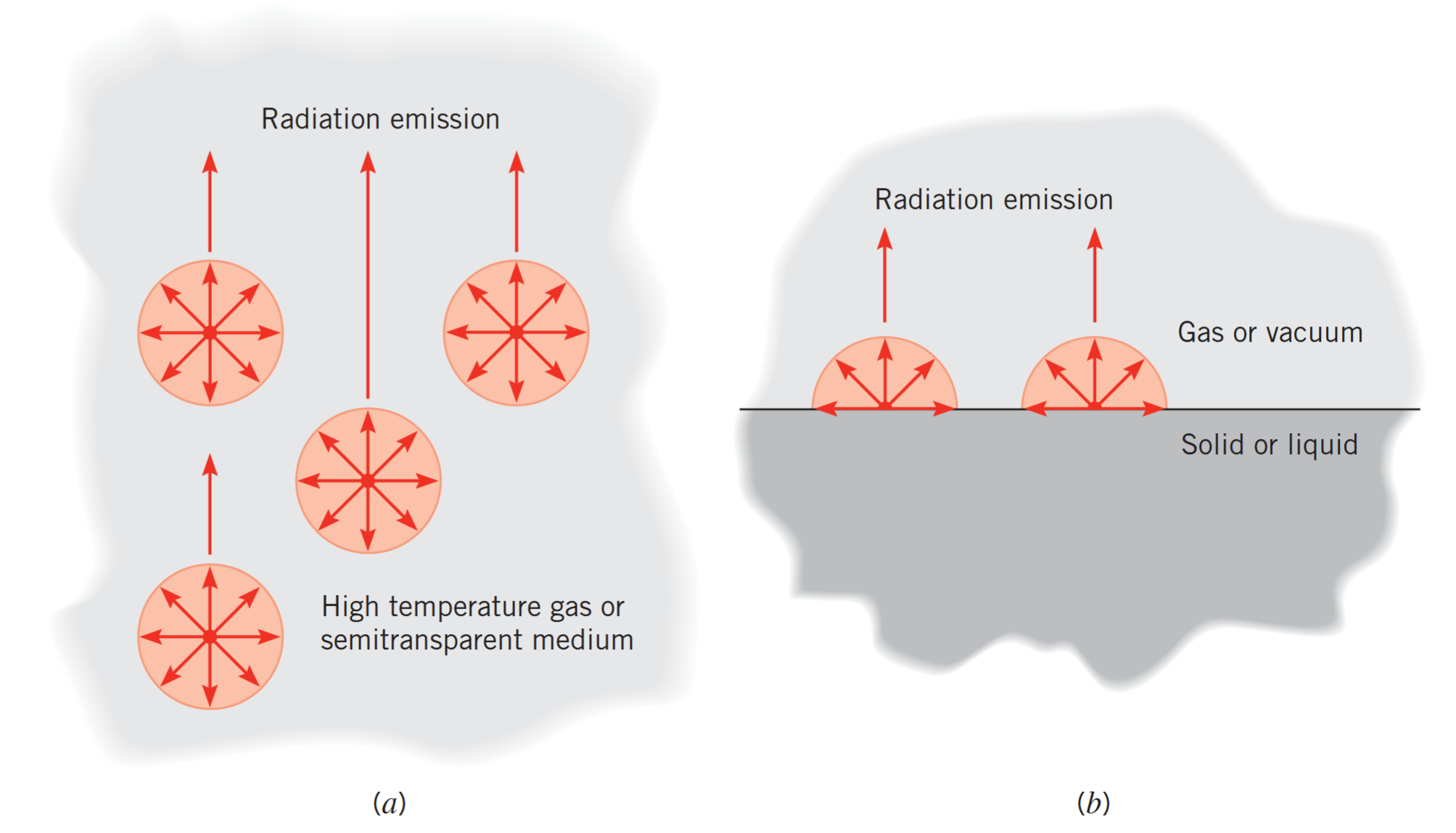
תהליך הפליטה. (a) כתופעה נפחית. (b) כתופעה משטחית. (Bergman & Lavine, 2017).

בקורס אנו נתעסק בעיקר במקרים שבהם נוכל להתייחס לקרינה כ-תופעה משטחית. ברוב המוצקים והנוזלים שפולטים קרינה לגז או ריק, נוכל להניח שזהו המצב.

באיור הבא מתואר הספקטרום האלקטרומגנטי:

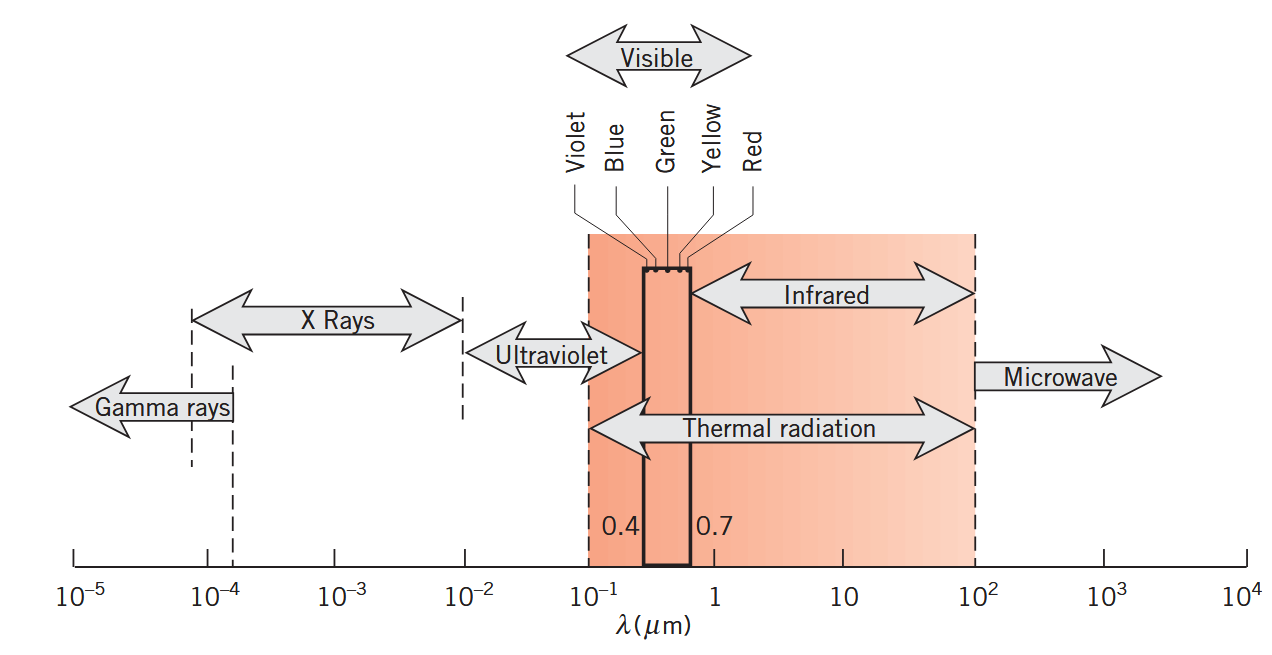
הספקטרום האלקטרומגנטי. (Bergman & Lavine, 2017).

בתור מהנדסים תרמיים, מעניין אותנו בעיקר תחום גלי האור באורכים של עד , שהוא מכיל חלק מתחום הקרינה האולטרה-סגול, כל האור הנראה וקרינה אינפרה-אדומה. לתחום זה אנו קוראים קרינה תרמית כי הוא בעיקר נוצר, ומשפיע ,על המצב התרמי או הטמפרטורה של המסה.
קרינה תרמית הנפלטת ע”י משטח יכולה לכלול טווח מאוד רחב של אורכי גל. כפי שניתן לראות מהאיור הבא, עוצמת הקרינה משתנה כתלות באורך גל, והמונח ספקטרלי בא להתייחס לאופן תלות זה:

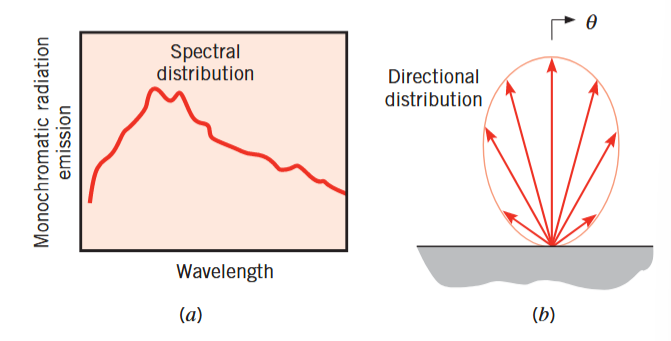
קרינה הנפלטת ממשטח. (a) פילוג ספקטרלי. (b) פילוג כיווני. (Bergman & Lavine, 2017).

הפילוג הספקטרלי הוא אחד משני מאפיינים של קרינה תרמית המסבך בעיות קרינה. המאפיין השני הוא ה-כיווניות. כפי שניתן לראות באיור לעיל, משטח יכול לפלוט קרינה בכיוון מסוים יותר מאשר כיוונים שונים, מה שיוצר פילוג כיווני בקרינה הנפלטת. לפליטה/החזרת קרינה כזו אנו אנו קוראים פליטה/החזרה דיפוזית (diffuse reflection/emissivity).

שטף חום בקרינה

בטבלה 12.1 מתוארים 4 סוגים שונים של שטפי חום בקרינה עוצמת הפליטה (emissive power) היא הקצב בו הקרינה נפלטת מהמשטח ליחידת שטח (), לאורך כל אורכי הגל ובכל הכיוונים. בקרינה, עוצמת קרינה זו הייתה קשורה להתנהגות של גוף שחור לפי , כאשר הוא תכונה של המשטח הנקראת אמיסיביות (emissivity).
בנוסף, קרינה מהסביבה, שיכולה לכלול מספר רב של משטחים בטמפרטורות שונות, פוגעת במשטח. המשטח יכול גם לקלוט קרינה ע”י השמש או ע”י לייזר. בכל מקרה, אנו מגדירים את קליטה זו כ-אירדיאציה (irradiation) - הקצב בו קרינה נקלטת ע”י המשטח ליחידת שטח (). את שני השטפי חום האחרים נגדיר בהמשך.

כאשר קרינה פוגעת במשטח שקוף למחצה, חלק מהאירדיאציה יכול לחזור (reflected) מהמשטח, חלק יכול להיבלע (absorbed) במשטח, וחלק יכול לעבור (transmitted) דרך המשטח, כפי שמתואר באיור הבא:

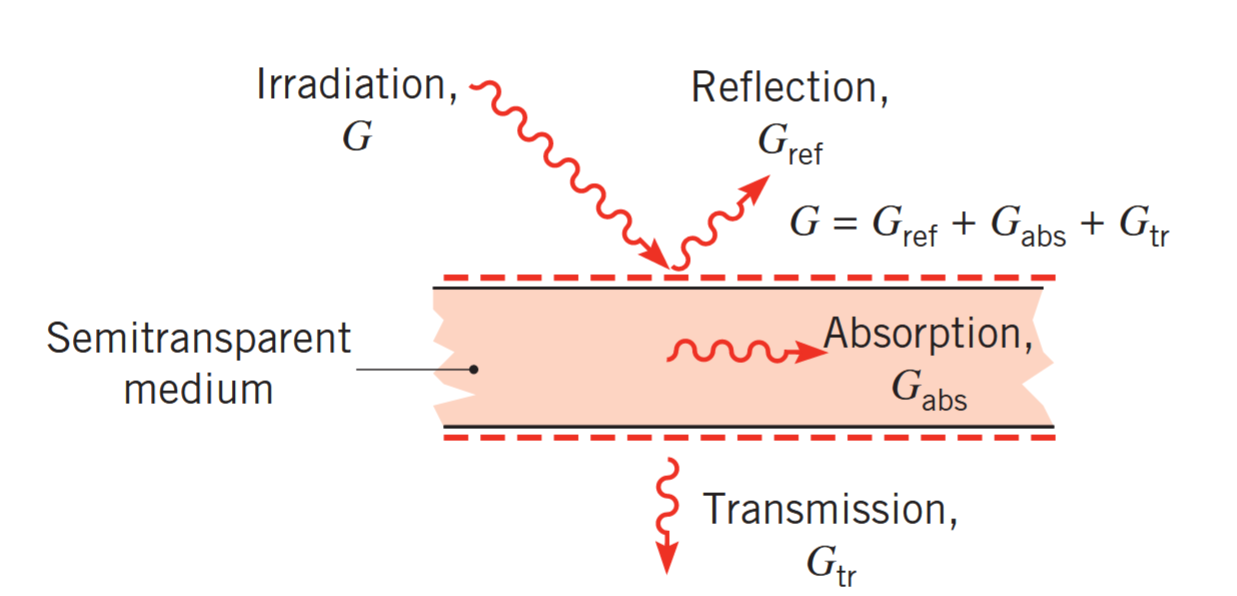
החזרה, בליעה, והעברה של קרינה בתווך שקוף למחצה. (Bergman & Lavine, 2017).

אנו מגדירים יחס החזרה (reflectivity) כחלק של האירדיאציה שמוחזר, יחס בליעה (absorptivity) כחלק שנבלע, ויחס העברה (transmissivity) כחלק שעובר. כיוון שכל האירדיאציה מוחזר, נבלע, או עובר, נסיק ש:

עבור חומר אטום, אין העברה (), ואז:

כעת, נוכל להגדיר עוד שני שטפי חום שיעזרו לנו. ה-רדיוסיטיות (Radiosity) של משטח הוא סך כל האנרגיה שעוזבת את המשטח בקרינה. למשטח אטום, הוא כולל פליטה והחזרה של קרינה, כפי שמוצג באיור הבא:

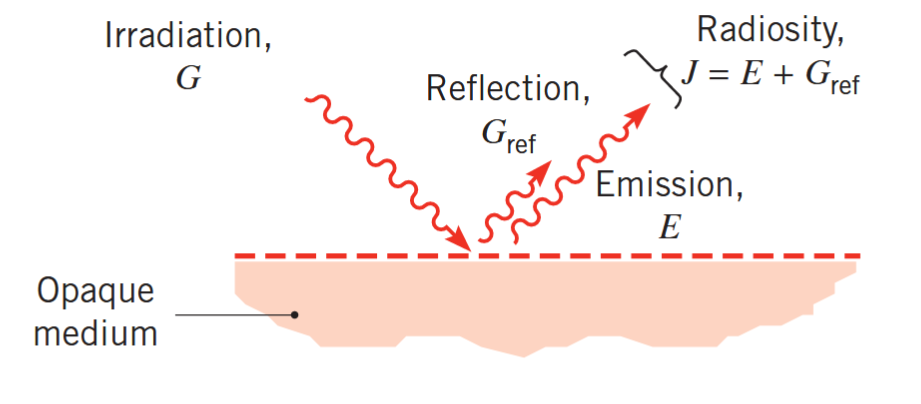
קרינה של חומר אטום. (Bergman & Lavine, 2017).

לכן נוכל לרשום אותה כ:

נוכל להגדיר רדיוסיטיות גם עבור משטח של תווך שקוף למחצה. במקרה זה, הרדיוסיטיות שעוזב את המשטח העליון יכלול גם את הקרינה העוברת דרך התווך מלמטה.

לבסוף, סך שטף החום הקרינתי מ-הקרינה, , הוא ההפרש בין הקרינה הנכנסת והקרינה היוצאת:

נוכל לשלב את המשוואות לעיל למשטח אטום ולקבל:

מקדם הראייה

כדי לחשב את הקרינה בין שני משטחים, עלינו קודם להציג את המונח מקדם הראייה (view factor).

אינטגרל מקדם הראייה

הגדרה: מקדם ראייה

מקדם הראייה מוגדר כהיחס של הקרינה העוזב את משטח ופוגע במשטח .

כדי לפתח ביטוי כללי ל-, נביט בשני משטחים שרירותיים ו-.

מקדם הראייה בין שטחים דיפרנציאליים ו-. (Bergman & Lavine, 2017).

מהגדרת עוצמת הקרינה, ניתן להראות לאחר מספר פיתוחים ש:

בהנחה ומשטח פולט ומחזיר באופן דיפוזי, וכאשר הוא הרדיוסיטיות של משטח .

לאחר אינטגרציה:

כאשר אנו מניחים שהרדיוסיטיות אחידה לאורך משטח . מהגדרת מקדם הראייה:

נסיק ש:

קשרי מקדם ראייה

נשים לב מ-(IH13.1) שמתקיים יחס הדדיות:

בנוסף, מהאיור הבא:

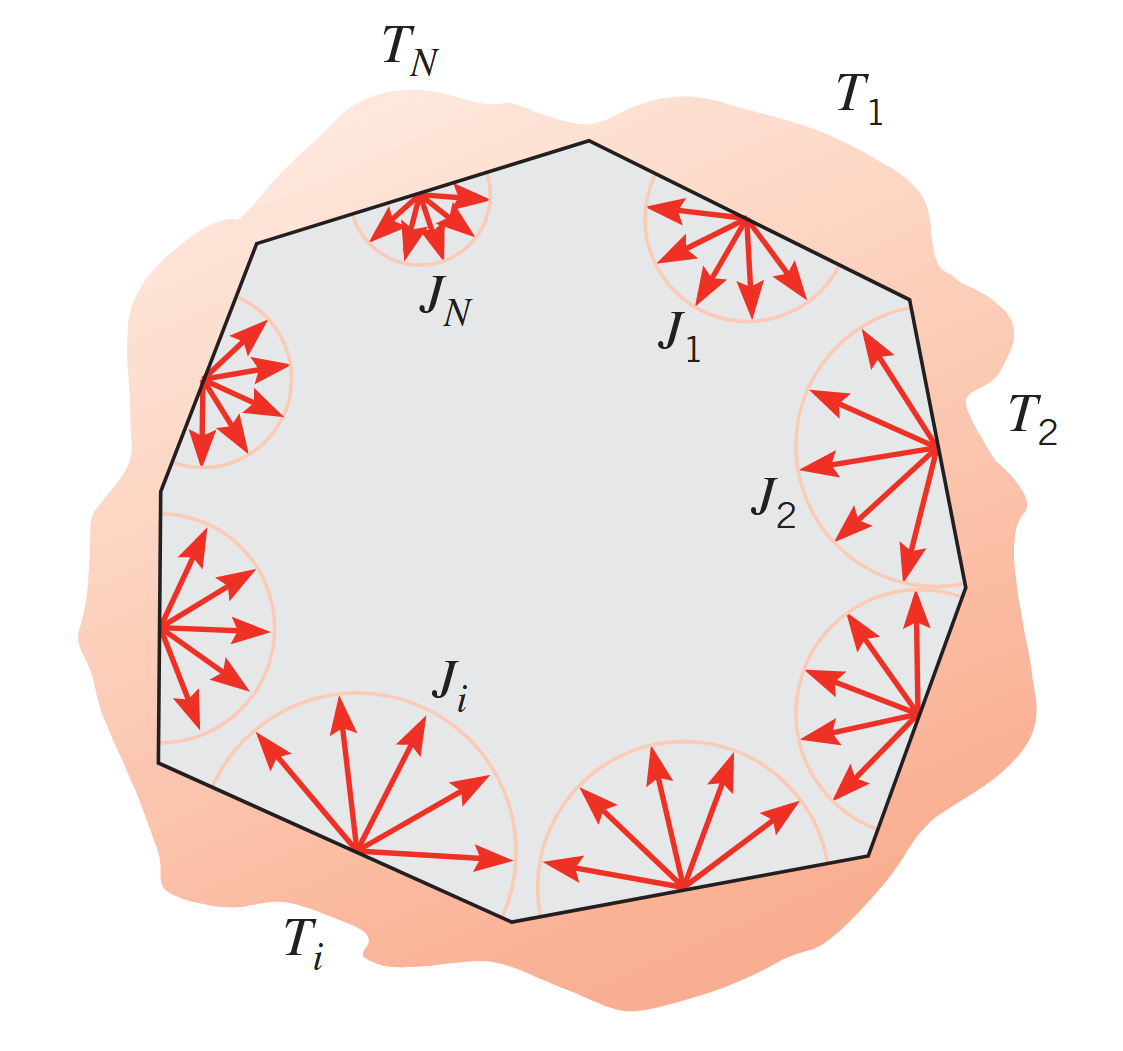
החלפת קרינה מתוחם. (Bergman & Lavine, 2017).

ניתן להסיק את מה שנקרא עקרון שלמות הראייה/כלל הסכימה:

הביטוי המופיע בסכימה זו הוא היחס של הקרינה העוזבת את משטח ופוגעת ישירות באותו המשטח, . אם המשטח קעור, הוא “רואה את עצמו”, ו- לא אפסי. אבל, עבור משטח קמור או שטוח, .

כדי לחשב את החלפת הקרינה בתחום סגור ע”י משטחים, אנו צריכים מקדמי ראייה. “קל” לראות זאת אם נסדר את מקדמי הראייה במטריצה:

אבל, לא צריכים לחשב את כל המקדמים באופן ישיר. ניתן למצוא מקדמים ע”י עקרון שלמות הראייה. בנוסף, ניתן למצוא מקדמים ע”י יחס ההדדיות. לכן, נצטרך לחשב רק מקדמים באופן ישר. למשל, עבור אזור המתוחם ע”י שלושה משטחים צריך לחשב רק מקדמי צורה באופן ישיר.

כדי להמחיש את הטענות לעיל, נביט כעת במערכת הסגורה הבאה:

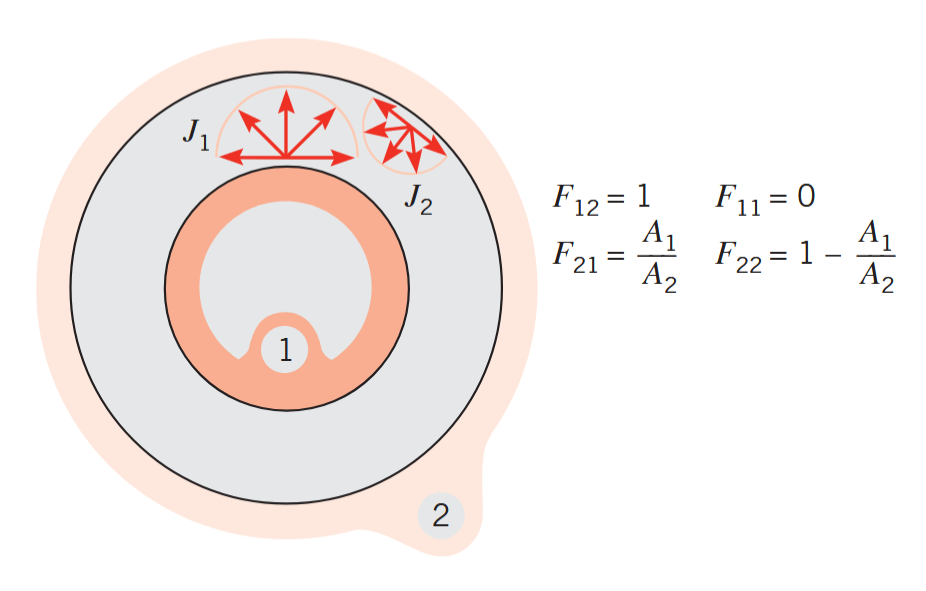
מקדמי ראייה לתחום בין שני כדורים. (Bergman & Lavine, 2017).

למרות שהתחום מוגדר ע”י מקדמי ראייה (), אנו צריכים לחשב רק מקדמים. נשים לב שמאחר וכל הקרינה העוזבת את המשטח הפנימי חייבת להגיע למשטח החיצוני, נסיק ש- . אנו לא יכולים לומר את אותו הדבר לקרינה העוזבת את המשטח החיצוני, מאחר ומשטח זה “רואה” את עצמו. אבל, לפי יחס ההדדיות, נמצא ש:

מעקרון שלמות הראייה:

וגם:

לגאומטריות יותר מסובכות, נעבור כבר לטבלה 13.1, או פשוט לאיורים 13.4-13.6.

נעבור כעת על עוד שני קשרים מאוד שימושיים בחישוב מקדמי הראייה. הראשון עוסק ב-חיבור מקדמי ראייה של משטחים:

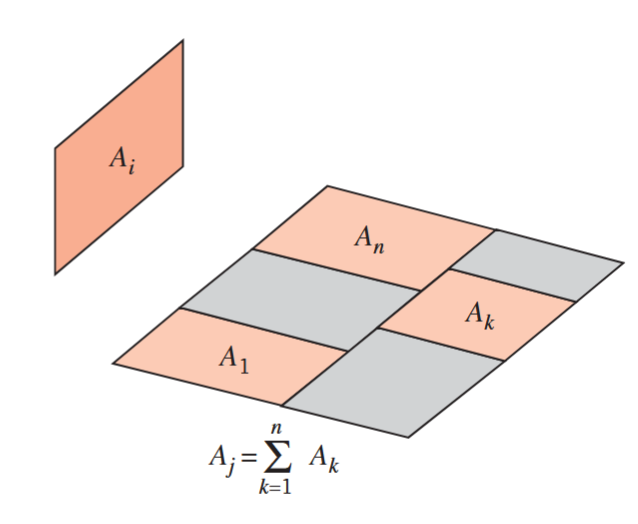
שטחים לתיאור קשרי מקדמי ראייה.

ניתן לראות שהמקדם קרינה ממשטח למשטח , שמחולק ל- חלקים, מקיים:

כאשר הסוגריים על מצביעים על כך שמדובר במשטח הכולל משטחים אחרים. ביטוי זה קובע שקרינה המגיעה למשטח כולל הוא סכום הקרינה שמגיע לכל חלקיו.
אם נכפיל את (IH13.5) ב- ונפעיל את קשר ההדדיות לכל אחד מהתוצאות שמתקבלות, נקבל:

כך ש:

קרינת גוף שחור

בכללי, קרינה עוזבת משטח מסוים כתוצאה מהחזרה ופליטה, ובהגעתו למשטח שני, הוא חווה חזרה וגם בליעה. אבל, המקרה יותר פשוט אם מדובר בגוף שחור, מאחר ואין החזרה. לכן, במקרה זה, האנרגיה עוזבת רק כתוצאה מפליטה, וכל הקרינה הפוגעת במשטח השני תיבלע.

נביט למשל בהחלפת קרינה בין שני משטחים שחורים בצורה כללית.

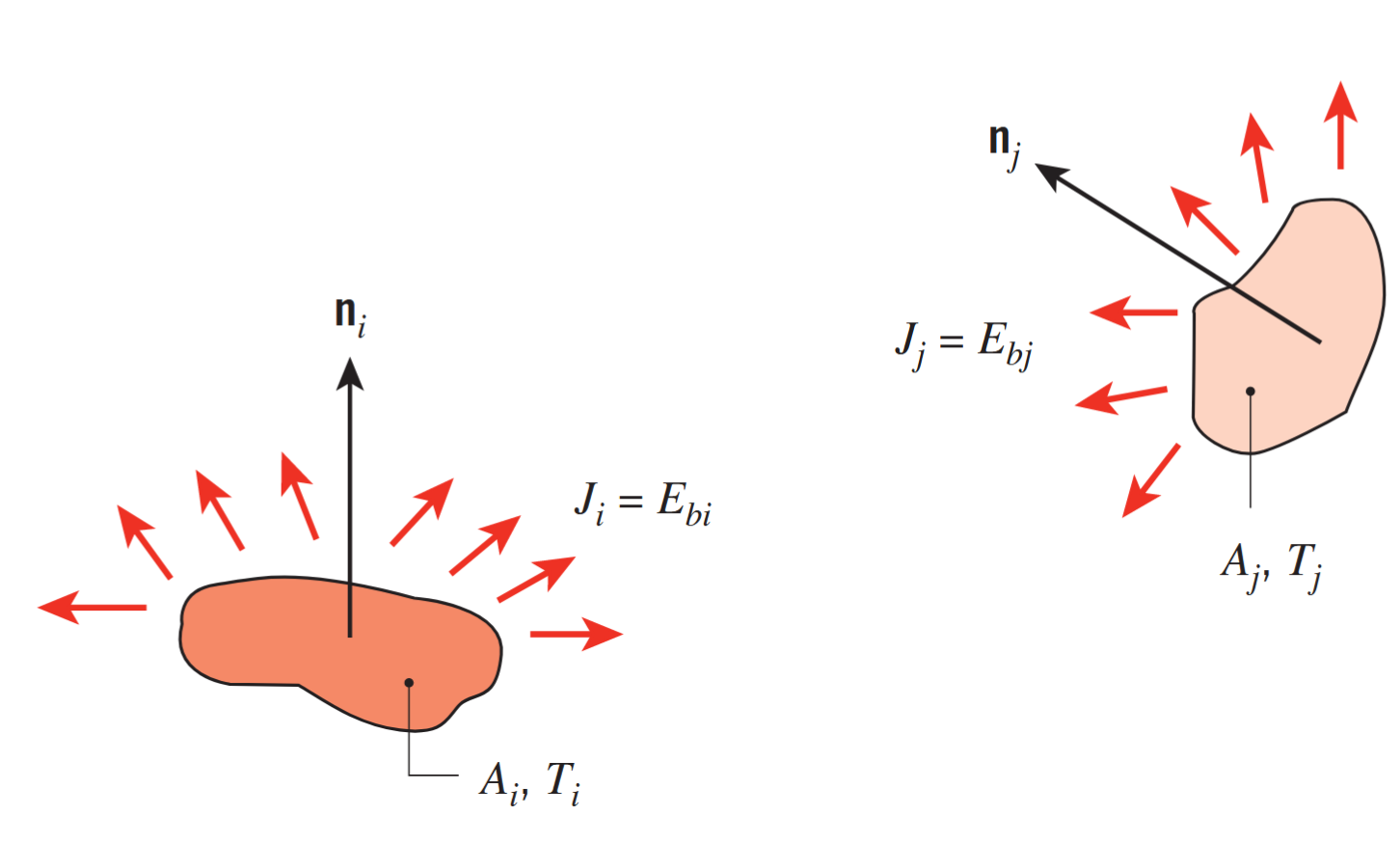
מעבר קרינה בין שני משטחים שניתן לקירובם לגופים שחורים. (Bergman & Lavine, 2017).

אם נגדיר כקצב בו קרינה עוזבת את משטח ופוגעת במשטח , נסיק ש:

או, מאחר והרדיוסיטיות שווה לעוצמת הפליטה של גוף שחור:

באותו אופן:

סך המעבר הקרינתי בין שני המשטחים מוגדר כ:

נסיק מכך:

או, ממשוואות (IH12.32) ו-(IH13.3):

משוואה זו נותנת את סך קצב מעבר החום בקרינה ה-עוזבת את משטח כתוצאה מ-, ששווה לסך קצב מעבר החום בקרינה ש- מקבל כתוצאה מ-.

נוכל להשתמש בתוצאה זו כדי למצוא את קצב מעבר החום בקרינה מכל משטח בתחום סגור של משטחים שחורים. עם משטחים הנשמרים בטמפרטורות שונות, סך קצב מעבר החום של קרינה ממשטח הוא כתוצאה מהמעבר עם שאר המשטחים, והוא ניתן לביטוי כ:

הערות: טעויות נפוצות

1. הטמפרטורות ו- ביחידות של קלוין !
2. שימו לב ש:

מעבר קרינה בין משטחים אטומים, דיפוזיים ואפורים בתחום סגור

בכללי, קרינה יכולה לעזוב משטח אטום כתוצאה מהחזרה ופליטה, וכאשר היא תגיע למשטח אטום אחר, היא תחווה גם החזרה וגם בליעה. בתחום סגור, כמו באיור הבא, הקרינה יכולה לחוות מספר החזרות מכל המשטחים, עם בליעה חלקית המתרחשת בכל אחד מהם.

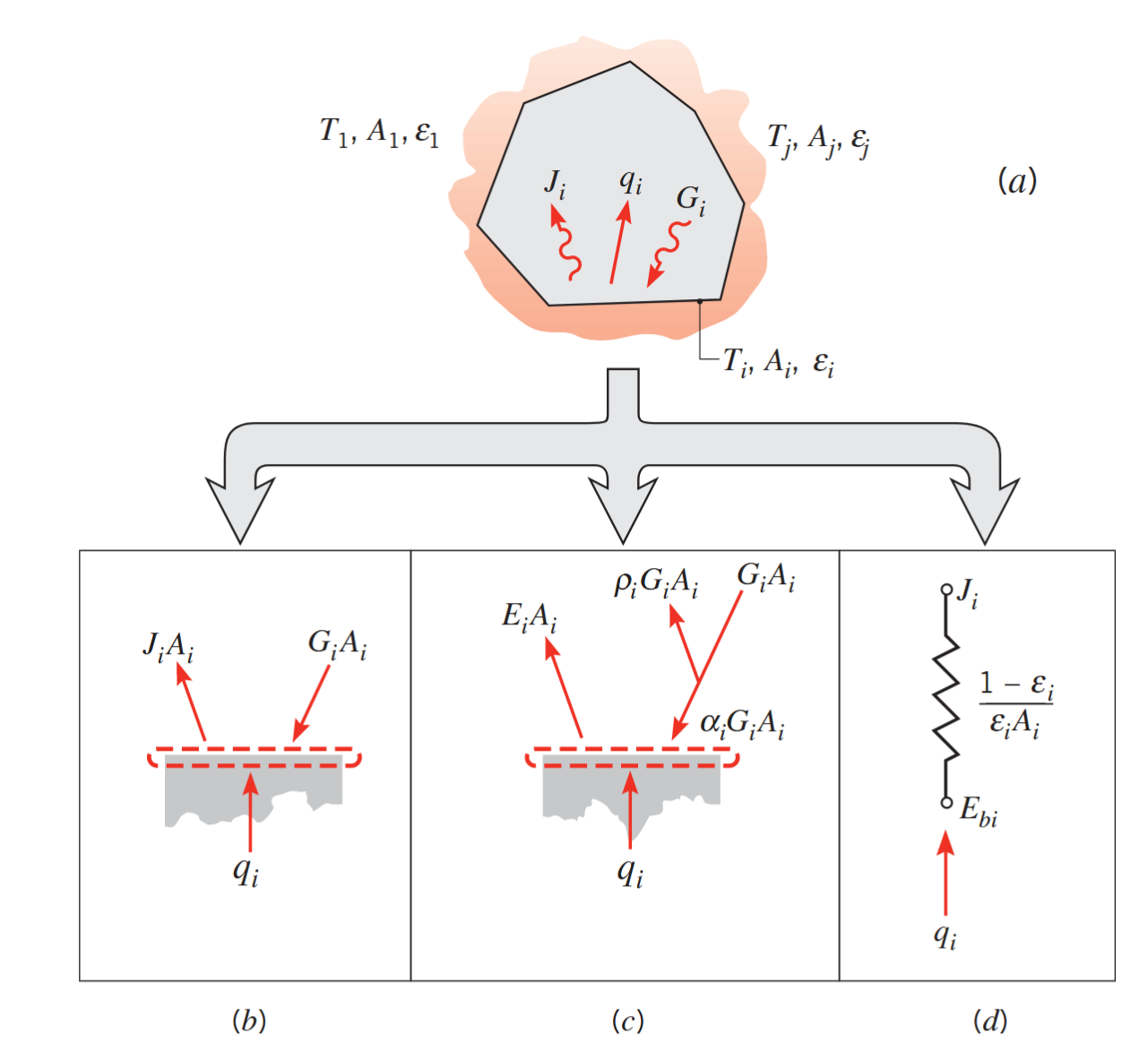
מעברי קרינה בתחום סגור ע”י משטחים דיפוזיים ואפורים. (a) סכמה של התחום הסגור. (b) מאזן קרינה לפי משוואה (IH13.15). (c) מאזן קרינה לפי משוואה (IH13.17). דיאגרמת נגדים למעבר קרינה ממשטח, משוואה (IH13.19). (Bergman & Lavine, 2017).

כדי לנתח את ה-חילופי קרינה בתחום סגור זה, נוכל לבצע מספר הנחות שיפשטו לנו את הבעיה. נניח שכל משטח הוא איזותרמי, עם רדיוסיטיות אחידה, ואירדיאציה אחידה. נניח גם שהמשטחים אטומים () ויש להם אמיסיביות, יחס בליעה, ויחס החזרה שלא תלויים בכיוון (המשטחים הם דיפוזיים), ולא תלויים באורך הגל (המשטחים הם אפורים). ניתן להראות שתחת תנאים אלו, יחס הבליעה זהה לאמיסיביות . כלומר, שמתקיים . אנו נבחן בעיות בהם אנו יודעים או את הטמפרטורה או שטף החום של כל משטח, ונצטרך למצוא את שטפי החום והטמפרטורות הלא ידועות של כל אחד מהמשטחים.

סך מעבר קרינה במשטח

הביטוי , שהוא סך קצב מעבר החום בו קרינה עוזבת את משטח , מייצג את סך ההשפעה של אינטראקציות קרינה המתרחשים במשטח (איור לעיל, (b)). הוא הקצב בו אנרגיה הייתה עוברת למשטח בדרכים אחרות כדי לשמור על טמפרטורה קבועה. הוא שווה להפרש בין הרדיוסיטיות והאירדיאציה, וממשוואה (IH12.5), נוכל לבטא אותו כ:

מהגדרת הרדיוסיטיות, משוואה (IH12.4):

לכן, נוכל לרשום את סך מעבר הקרינה ממשטח מסוים כ:

כאשר , כי אנו מניחים שהמשטח אטום.
נשים לב ש- (כאשר הוא עוצמת הפליטה אם הגוף היה שחור), וגם למשטח אטום, דיפוזי, ואפור, ולכן ניתן לרשום את הרדיוסיטיות כ:

אם נפתור עבור , ונציב את משוואה , נסיק כי:

לאחר קצת סידור:

משוואה זו נותנת לנו קשר בין הפרש פוטנציאלים המניע את מעבר החום, ו-התנגדות משטחית לקרינה מהצורה . לכן, אם עוצמת הפליטה שהיה למשטח אם הוא היה שחור, , גדול יותר מהרדיוסיטיות שלו, סך המעבר חום בקרינה הוא אל המשטח. במקרה ההפוך, סך מעבר החום בקרינה יהיה מ-המשטח.

בחלק מהמקרים אחד מהמשטחים גדול בהרבה משאר המשטחים. ניתן לראות מהמשוואה לעיל שאם באמת עבור אחד מהמשטחים נוכל לקרב , ההתנגדות המשטחית שלו לקרינה, , היא תאכלס אפסית, בדיוק כמו שהיא עבור גוף שחור (). לכן, יתקיים , כך שנוכל לומר ש-נוכל להתייחס למשטח שיחסית גדול יותר מכל שאר המשטחים כגוף שחור. ההסבר הפיזיקלי לכך הוא שלמרות שהגוף הגדול מחזיר חלק מהאירדיאציה עליו, הוא כל כך גדול כך שיש סיכוי די גבוה שהקרינה המחוזרת תגיע לעוד נקודה על אותו משטח גדול. לאחר מספר החזרות כאלו, כל הקרינה שבמקור הוחזרה ע”י המשטח הגדול נבלעת על ידיו, ולא מגיע אף פעם לשאר המשטחים הקטנים.

סך מעבר קרינה בין משטחים

כדי להשתמש ב-(IH13.19), עלינו לדעת מהי הרדיוסיטיות של המשטח . כדי למצוא את גודל זה, נצטרך לקחת בחשבון את מעברי הקרינה בין המשטחים בתחום הסגור.
האירדיאציה של משטח ניתנת לחישוב מהרדיוסיטיות של כל המשטחים בתחום הסגור. בפרט, מהגדרת מקדם הראייה, נסיק שסך הקצב בו קרינה מגיעה למשטח מכל המשטחים, כולל , הוא

מתוך יחס ההדדיות, (IH13.3):

מחילוק בשטח ומהצבת (IH13.15) עבור :

מעקרון שלמות הראייה, (IH13.4):

לכן:

שיטת הנגדים לקרינה

ממשוואות (IH13.19) ו-(IH13.20) נוכל לקבל ש:

כפי שניתן לראות מהאיור הבא, ביטוי זה מתאר מאזן קרינה לצומת בתרשים נגדים לקרינה:

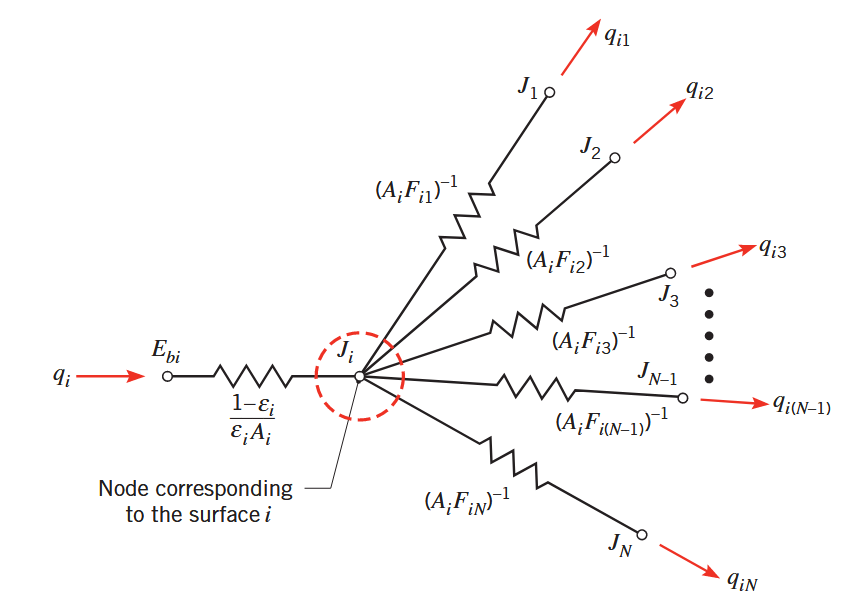
תרשים נגדים למעבר קרינה בין משטח לכל המשטחים בתחום סגור.

קצב מעבר הקרינה ל- דרך התנגדות המשטח חייב להיות שווה לקצב מעבר הקרינה מ- לכל שאר המשטחים דרך ההתנגדויות הגאומטריות המתאימות.

הערה:

ההתנגדויות כאן הן לא התנגדויות תרמיות, אלא התנגדויות לקרינה. אם נרצה להיות יותר מדויקים, נוכל לומר שהם התנגדויות ל-רדיוסיטיות, וניתן לפתור בעיות בעזרת תרשים נגדים זה כמו שעשינו עבור נגדים תרמיים, רק שנשים לב שהפעם במקום הפרשי טמפרטורות, מה שמניע את מעבר החום הוא הפרשי פוטנציאלים של הקרינה. כמובן שגם היחידות של התנגדויות אלו שונות.

נשים לב שמשוואה (IH13.21) מאוד שימושית כאשר טמפרטורות המשטח (ולפיכך ) ידועה. למרות שמקרה זה די טיפוסי, הוא לא תמיד המצב. ישנם מקרים עבורם סך קצב מעבר הקרינה במשטח , במקום הטמפרטורה , ידוע. במצבים אלו נעדיף להשתמש בתצורה הבאה למאזן קרינה, הנובעת ממשוואה (IH13.20):

דוגמה: 13.4 בספר

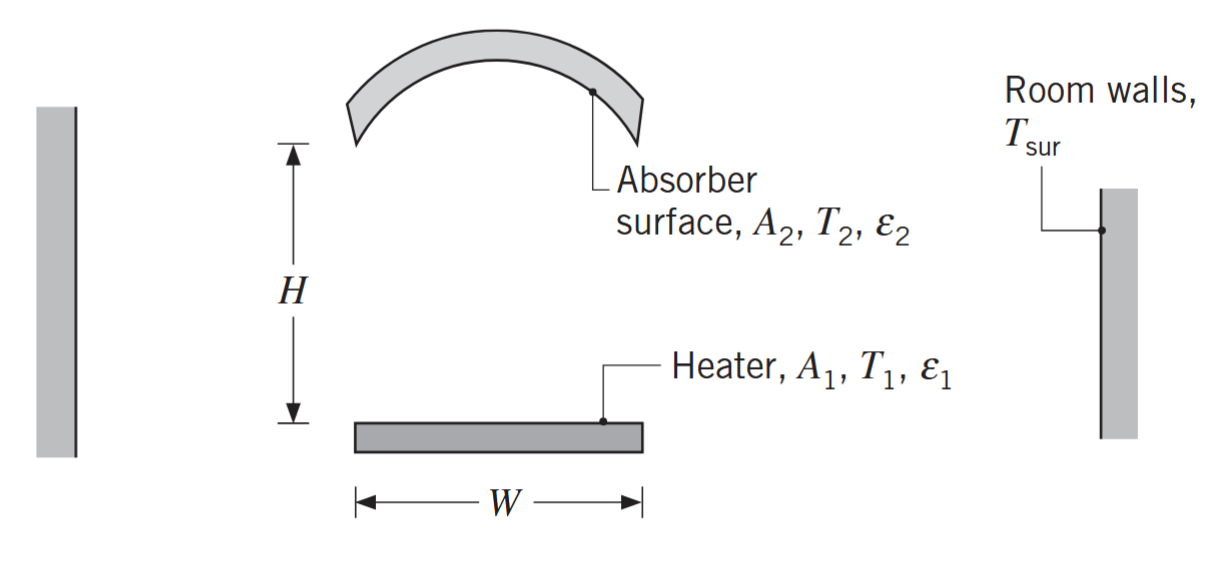
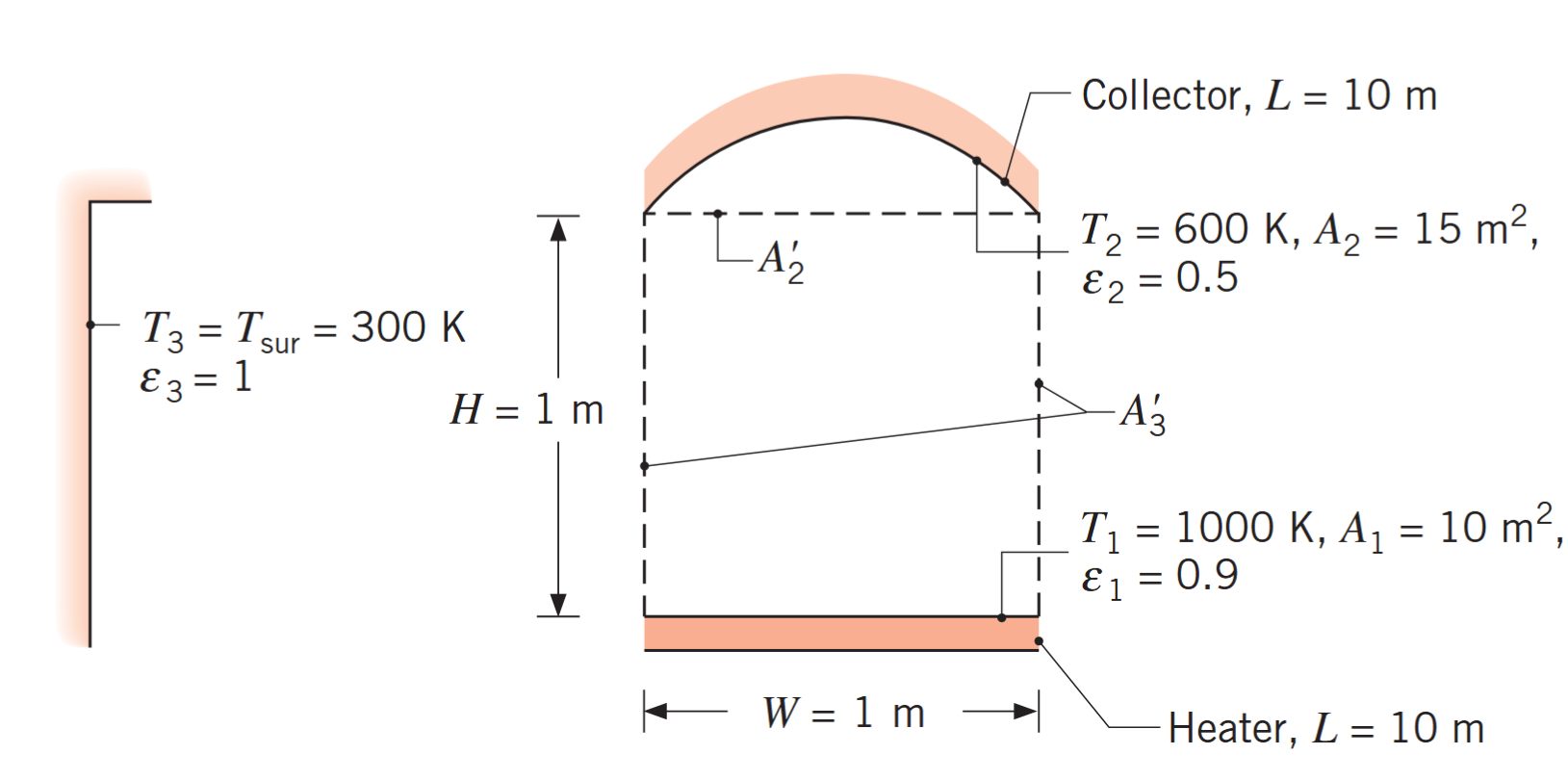
בתהליך ייצור מסוים, מצפים קולט סולארי בשטח ע”י חשיפתו למחמם אינפרא-אדום ברוחב . הקולט והמחמם שניהם באורך והם מופרדים ע”י מרחק של . המשטח העליון של הקולט והתחתון של המחמם מבודדים.

המחמם הוא בטמפרטורה של עם אמיסיביות , כאשר הקולט הוא ב- עם אמיסיביות של . המערכת נמצאת בחדר גדול שקירותיו ב-. מהו קצב מעבר החום למשטח הקולט?

פתרון:

הנחות:

1. מצב מתמיד.
2. הסעה זניחה.
3. הקולט ומשטחי המחמם דיפוזיים ואפורים ומאופיינים באירדיאציה ורדיוסיטיות אחידה.
4. הסביבה (החדר) גדול ולכן מתפקד כגוף שחור.

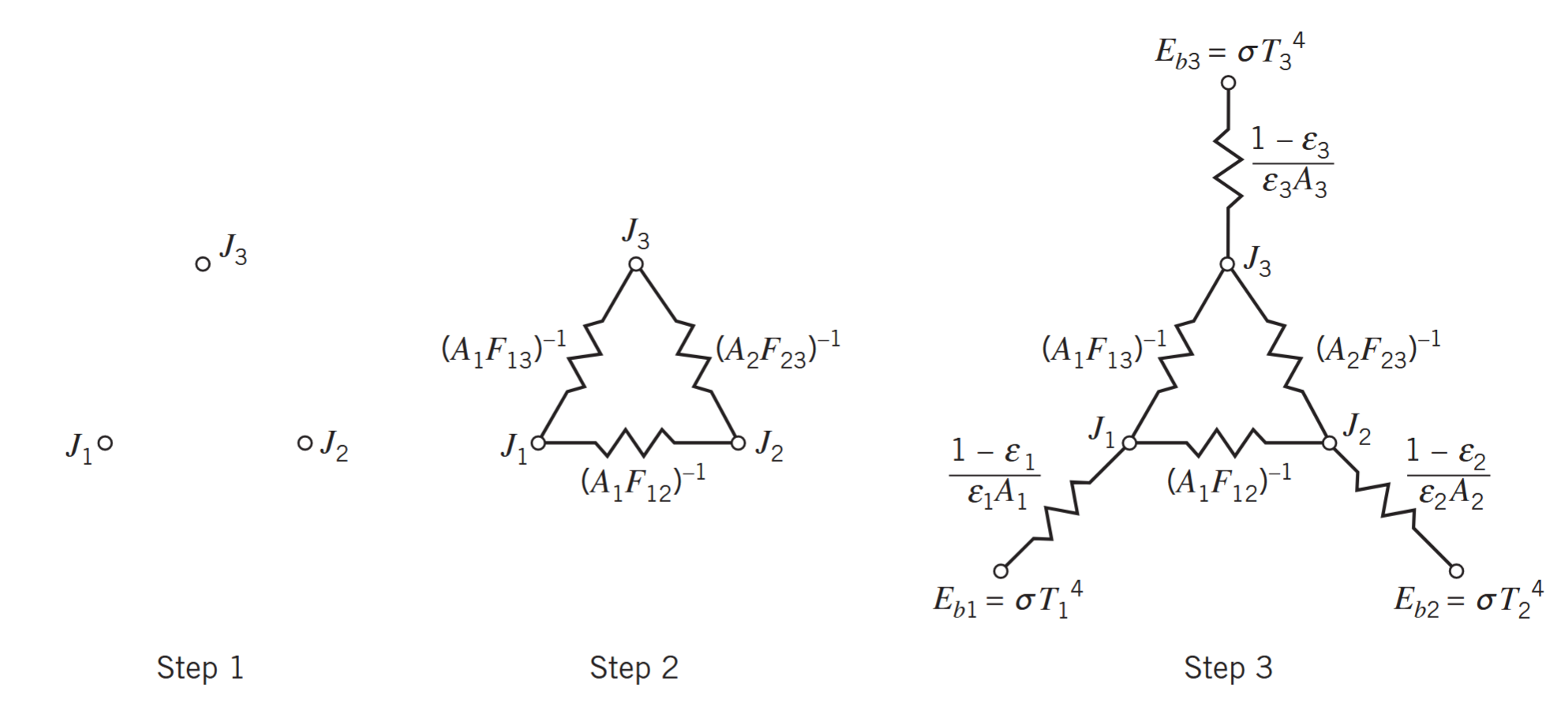
נוכל לחשוב על המערכת הנתונה כתחום סגור עם שלושה משטחים, כאשר המשטח השלישי הוא החדר, שמתפקד כגוף שחור. נרצה למצוא את קצב מעבר הקרינה למשטח . נפתור את הבעיה לפי שיטת הנגדים.

נתחיל קודם מבחירת צמתי רדיוסיטיות בהתאמה לכל משטח. לאחר מכן נחבר כל צומת לכל אחד מהצמתים האחרים דרך ההתנגדות המרחבים המתאימה. לבסוף, נחבר את עוצמת הפליטה של גוף שחור של כל משטח לצומת המתאימה, דרך ההתנגדות המשטחית המתאימה.

לפי הנחה (4), ההתנגדות המשטחית של משטח היא אפס, כך ש- .

נסכום את הזרמים דרך צומת לקבלת:

כאשר נסכום את הזרמים דרך :

נשים לב ש- , כאשר בסכמה לעיל הוא הבסיס המלבני של הקולט. לכן, מאיור 13.4 עם וגם :

מעקרון שלמות הראייה, ומכך ש- , נסיק ש:

נשים לב גם שמאחר והקרינה המתקדמת ממשטח ל- חייבת לעבור דרך השטח ההיפותטי ,

ומהסימטריה . לכן:

נוכל כעת לפתור את (1) ו-(2) עבור . נציב נתונים ונקבל ש:

מהתרשים נגדים לעיל נוכל כעת למצוא את סך קצב מעבר החום מ-הקולט:

לכן סך מעבר החום אל הקולט הוא .

משטח מבודד מצד אחד

בהרבה מן המקרים נוכל להניח שמשטח מבודד היטב מצד אחד, שניתן להזניח בו הסעה על הצד (המקרין) האחר, הוא משטח אידיאלי עם אפס מעבר בקרינה . כאשר , נובע ממשוואות (IH13.15) ו-(IH13.19) ש- . לכן, הרדיוסיטיות של משטח אידיאלי זה (הנקרא גם reradiating surface) ידוע.

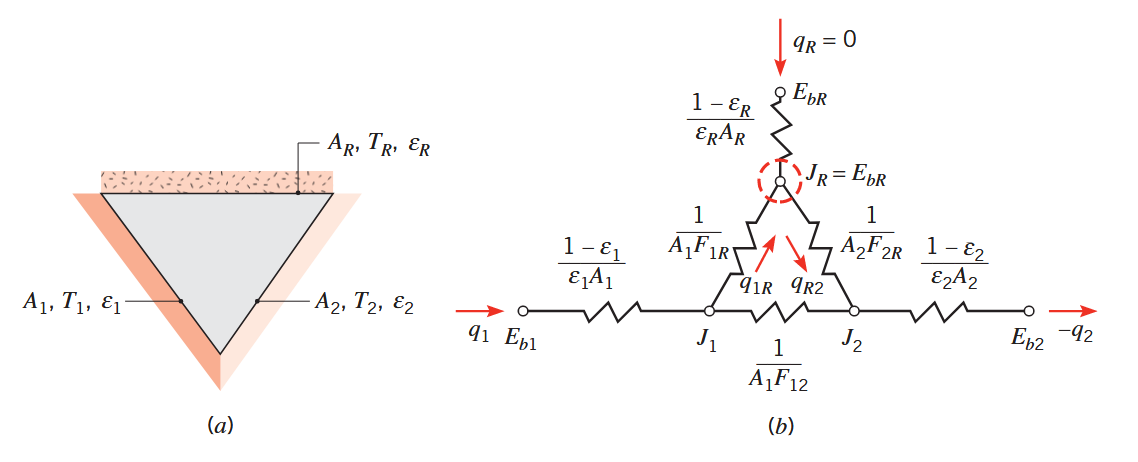
תחום סגור ע”י שלושה משטחים, עם אחד אידיאלי.

→ קודם: HTF1_008