פנגייה

PHY3_001 מבוא לפיזיקה קוונטית א

• זמן קריאה: 25 דק'

קרינת גוף שחור והיפותזת פלאנק

כפי שלמדנו ב-מעבר חום, כל גוף בכל טמפרטורה פולט גלים אלקטרומגנטיים בצורה של קרינה תרמית מפני השטח שלו. המאפיינים של קרינה זו תלויים בטמפרטורה ובתכונות של פני השטח של העצם. מחקרים מראים שהקרינה מורכבת מהתפלגות רציפה של אורכי גל מכל חלקי הספקטרום האלקטרומגנטי. אם העצם נמצא בטמפרטורת החדר, אורכי הגל של הקרינה התרמית נמצאים בעיקר באזור האינפרא-אדום ולכן הקרינה אינה מזוהה על ידי העין האנושית. כאשר טמפרטורת השטח של העצם עולה, העצם בסופו של דבר מתחיל לזהור באופן גלוי באדום, כמו הסלילים של טוסטר. בטמפרטורות גבוהות מספיק, העצם הזוהר נראה לבן, כמו בחוט הטונגסטן החם של נורת להט.

מנקודת מבט קלאסית, קרינה תרמית מקורה בחלקיקים טעונים מואצים באטומים ליד פני השטח של העצם; אותם חלקיקים טעונים פולטים קרינה דומה לאנטנות קטנות. החלקיקים הנסערים תרמית יכולים להיות בעלי התפלגות רחבה של אנרגיות, מה שמסביר את הספקטרום הרציף של הקרינה הנפלטת על ידי העצם.

עד סוף המאה ה-19, התברר שהתיאוריה הקלאסית של קרינה תרמית אינה מספקת. הבעיה הבסיסית הייתה בהבנת ההתפלגות הנצפית של אורכי גל בקרינה הנפלטת על ידי גוף שחור. גוף שחור הוא מערכת אידיאלית שבולעת את כל הקרינה הפוגעת בו; אין כלל השתקפות מפני השטח שלו. הקרינה האלקטרומגנטית הנפלטת על ידי הגוף השחור נקראת קרינת גוף שחור.

קירוב טוב מציאותי של גוף שחור הוא חור קטן המוביל לפנים של עצם חלול כפי שמוצג באיור הבא. כל קרינה הפוגעת בחור מחוץ לחלל נכנסת לחור ומוחזרת מספר פעמים על הקירות הפנימיים של החלל; לכן, החור פועל כבולע מושלם. טבע הקרינה היוצאת מהחלל דרך החור תלוי רק בטמפרטורה של קירות החלל ולא בחומר שממנו עשויים הקירות.

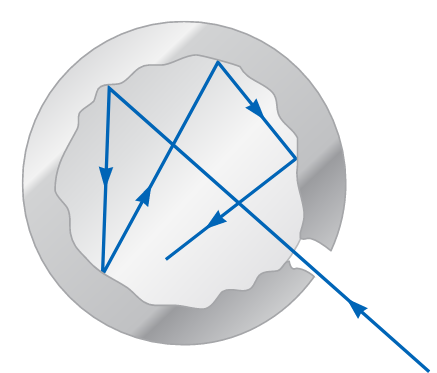
bookhue

איור 1.1: מודל פיזיקלי של גוף שחור. הפתח לחלל בתוך עצם חלול הוא קירוב טוב של גוף שחור: החור פועל כבולע מושלם. (Serway et al., 2019).

הקרינה הנפלטת על ידי מתנדים בקירות החלל באיור 1.1 חווה תנאי גבול וניתן לנתח אותה באמצעות מודל הניתוח של גלים תחת תנאי גבול המיושם על חלל תלת-ממדי. כאשר הקרינה מוחזרת מקירות החלל, גלים אלקטרומגנטיים עומדים נוצרים בפנים החלל. מצבי גל עומד רבים אפשריים, וההתפלגות של האנרגיה בחלל בין מצבים אלה קובעת את התפלגות אורכי הגל של הקרינה היוצאת מהחלל דרך החור.

בסוף המאה ה-19, חקרו רבות את התפלגות אורכי הגל של קרינה מחללים. האיור הבא מראה כיצד עוצמת קרינת גוף שחור משתנה עם טמפרטורה ואורך גל כפי שנקבע על ידי הניסויים האלה.
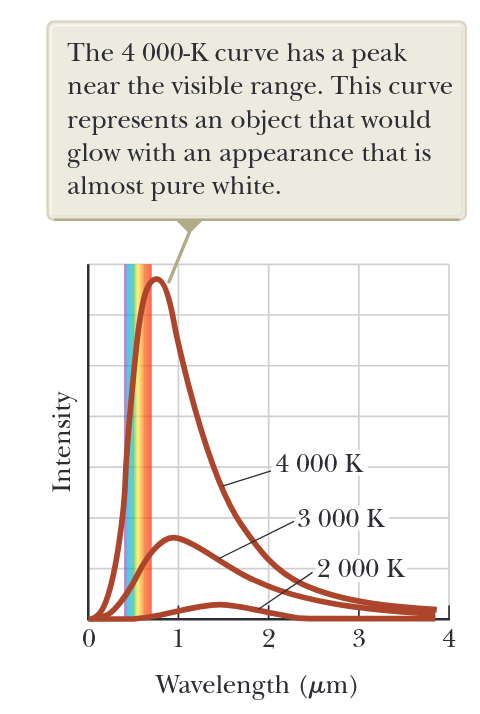
bookhue

איור 1.2: עוצמת קרינת גוף שחור כפונקציה של אורך גל בשלוש טמפרטורות. הטווח הגלוי של אורכי גל הוא בין ל-. בכ- בקירוב, השיא נמצא במרכז אורכי הגל הגלויים והעצם נראה לבן. (Serway et al., 2019).

שתי התוצאות הניסיוניות העקביות הבאות נראו כמשמעותיות במיוחד:

  1. הכוח הכולל של הקרינה הנפלטת עולה עם הטמפרטורה. - זהו חוק סטפן-בולצמן:

כאשר הוא ההספק בוואט המוקרן בכל אורכי הגל מפני השטח של עצם, הוא קבוע סטפן-בולצמן, הוא שטח הפנים של העצם במטרים רבועים, הוא אמיסיביות השטח, ו- הוא טמפרטורת השטח בקלווין. עבור גוף שחור, האמיסיביות היא בדיוק.

  1. השיא של התפלגות אורך הגל נעה לאורכי גל קצרים יותר כאשר הטמפרטורה עולה. התנהגות זו מתוארת על ידי הקשר הבא, הנקרא חוק ההעתקה של וין:

כאשר הוא אורך הגל שבו העקומה מגיעה לשיא ו- הוא הטמפרטורה המוחלטת של פני השטח של העצם הפולט את הקרינה. אורך הגל בשיא העקומה הוא ביחס הפוך לטמפרטורה המוחלטת; כלומר, כאשר הטמפרטורה עולה, השיא “נעתק” לאורכי גל קצרים יותר כפי שמוצג באיור 1.2.

תוצאות ניסיוניות אלה עקביות עם התנהגות חוט להט בנורת להט. בטמפרטורת החדר, החוט לא נראה זוהר כיוון שהשיא נמצא באזור האינפרא-אדום של הספקטרום האלקטרומגנטי. כאשר מתח מלא מופעל על החוט, הטמפרטורה שלו עולה להיות בסדר גודל של . רוב הקרינה מהחוט נמצאת באינפרא-אדום, אבל, כפי שניתן לראות מהעקומה האמצעית באיור 1.2, כמות משמעותית של קרינה גלויה בכל אורכי הגל נפלטת, מה שנותן תוצאה צהבהבה-לבנה. כאשר המתח יורד, החוט פועל בטמפרטורה נמוכה יותר. הוא הופך עמום יותר, בגלל חוק סטפן, והשיא בהתפלגות נע ימינה באיור 1.2. כפי שניתן לראות מהעקומה הנמוכה ביותר ב-, הקרינה הגלויה היא בעיקר מהקצה האדום של הספקטרום, מה שנותן לחוט מראה של זוהר כתום.

תיאוריה מוצלחת לקרינת גוף שחור חייבת לחזות את הצורה של העקומות באיור 1.2, את התלות בטמפרטורה המבוטאת בחוק סטפן, ואת ההעתקה של השיא עם הטמפרטורה המתוארת בחוק ההעתקה של וין.

ניסיונות מוקדמים להשתמש ברעיונות קלאסיים כדי להסביר את הצורות של העקומות נכשלו. בואו נבחן אחד מהניסיונות המוקדמים האלה.

כדי לתאר את התפלגות האנרגיה מגוף שחור, אנו מגדירים להיות העוצמה, או הספק ליחידת שטח, הנפלטת בפרק אורך הגל . התוצאה של חישוב המבוסס על תיאוריה קלאסית של קרינת גוף שחור הידועה כחוק ריילי-ג’ינס היא:

כאשר הוא קבוע בולצמן. הגוף השחור ממודל כחור המוביל לחלל כפי שמוצג באיור 1.1, מה שמביא למצבי תנודה רבים של השדה האלקטרומגנטי הנגרמים על ידי מטענים מואצים בקירות החלל ופליטת גלים אלקטרומגנטיים בכל אורכי הגל.

בתיאוריה הקלאסית המשמשת לגזירת משוואה (SJ39.3), האנרגיה הממוצעת עבור כל אורך גל של מצבי הגל העומד, מונחת להיות פרופורציונלית ל-.

האיור הבא מציג תרשים ניסיוני של ספקטרום קרינת גוף שחור, יחד עם החיזוי התיאורטי של חוק ריילי-ג’ינס.

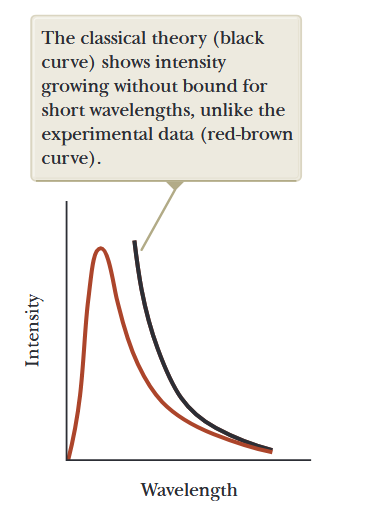
bookhue

איור 1.3: השוואה של תוצאות ניסיוניות והעקומה החזויה על ידי חוק ריילי-ג’ינס עבור התפלגות קרינת גוף שחור. התיאוריה הקלאסית מראה עוצמה הגדלה ללא גבול עבור אורכי גל קצרים, בניגוד לנתונים הניסיוניים (עקומה אדומה). (Serway et al., 2019).

באורכי גל ארוכים, חוק ריילי-ג’ינס נמצא בהסכמה סבירה עם הנתונים הניסיוניים, אבל באורכי גל קצרים, ישנה אי-הסכמה ברורה. כאשר מתקרב לאפס, הפונקציה הנתונה במשוואה (SJ39.3) מתקרבת לאינסוף. לכן, על פי התיאוריה הקלאסית, לא רק שאורכי גל קצרים צריכים להיות דומיננטיים בספקטרום גוף שחור, אלא גם האנרגיה הנפלטת על ידי כל גוף שחור צריכה להפוך אינסופית בגבול של אורך גל אפס.

בניגוד לחיזוי זה, הנתונים הניסיוניים המתוארים באיור 1.3 מראים שכאשר מתקרב לאפס, גם מתקרב לאפס. חוסר ההתאמה הזה בין תיאוריה וניסוי היה כל כך מטריד שמדענים קראו לזה האסון האולטרה-סגול (ultraviolet catastrophe. (ה”אסון” הזה - אנרגיה אינסופית - מתרחש כאשר אורך הגל מתקרב לאפס; המילה אולטרה-סגול הוחלה כיוון שאורכי גל אולטרה-סגול הם קצרים.)

בשנת 1900, מקס פלאנק פיתח תיאוריה של קרינת גוף שחור שמובילה למשוואה עבור שנמצאת בהסכמה מלאה עם התוצאות הניסיוניות בכל אורכי הגל. בדיון בתיאוריה זו, אנו משתמשים במתאר של תכונות מודלים מבניים:

  1. רכיבים פיזיקליים:
    פלאנק הניח שקרינת החלל הגיעה ממתנדים אטומיים בקירות החלל באיור 1.1, בדיוק כמו בגישת ריילי-ג’ינס.

  2. התנהגות הרכיבים:
    החלק הזה של המודל שונה לחלוטין מגישת ריילי-ג’ינס:

    • האנרגיה של מתנד יכולה להיות רק בעלת ערכים בדידים מסוימים :
     כאשר $n$ הוא מספר שלם חיובי הנקרא מספר קוונטי, $f$ הוא תדירות המתנד, ו-$h$ הוא פרמטר שפלאנק הכניס שנקרא כעת **קבוע פלאנק**. מכיוון שהאנרגיה של כל מתנד יכולה להיות רק בעלת ערכים בדידים הנתונים במשוואה $\text{(SJ39.4)}$, אנו אומרים שהאנרגיה **מקוונטת (quantized)**. כל ערך אנרגיה בדיד מתאים ל**מצב קוונטי** שונה, המיוצג על ידי המספר הקוונטי $n$. כאשר המתנד נמצא במצב הקוונטי $n = 1$, האנרגיה שלו היא $hf$; כאשר הוא במצב הקוונטי $n = 2$, האנרגיה שלו היא $2hf$; וכן הלאה.
    • המתנדים פולטים או בולעים אנרגיה כאשר הם עושים מעבר ממצב קוונטי אחד לאחר. כל ההפרש באנרגיה בין המצבים הראשוני והסופי במעבר נפלט או נבלע כקוונטום יחיד של קרינה. אם המעבר הוא ממצב אחד למצב סמוך נמוך יותר - נאמר, ממצב למצב - משוואה (SJ39.4) מראה שכמות האנרגיה הנפלטת על ידי המתנד והנישאת על ידי קוונטום הקרינה היא:

על פי התכונה השנייה מתנד פולט או בולע אנרגיה רק כאשר הוא משנה מצבים קוונטיים. אם הוא נשאר במצב קוונטי אחד, אין שום אנרגיה שנבלעת או שנפלטת.

האיור הבא הוא תרשים רמות אנרגיה המראה את רמות האנרגיה המקוונטות והמעברים המותרים שהוצעו על ידי פלאנק.

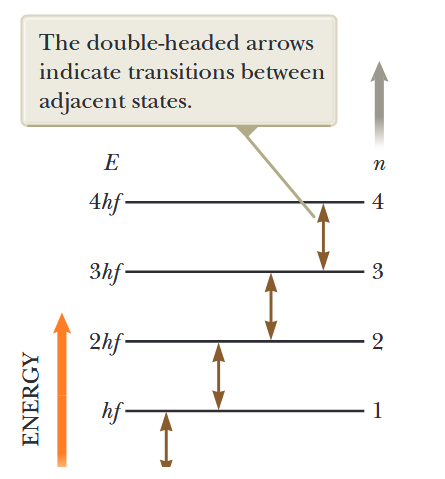
bookhue

איור 1.4: רמות אנרגיה מותרות עבור מתנד עם תדירות . (Serway et al., 2019).

הייצוג החצי-גרפי החשוב הזה משמש לעתים קרובות בפיזיקה קוונטית. הציר האנכי הוא לינארי באנרגיה, ורמות האנרגיה המותרות מיוצגות כקווים אופקיים. המערכת המקוונטת יכולה להיות בעלת רק האנרגיות המיוצגות על ידי הקווים האופקיים.

הנקודת המפתח בתיאוריית פלאנק היא ההנחה הרדיקלית של מצבי אנרגיה מקוונטים. הפיתוח הזה - סטייה ברורה מהפיזיקה הקלאסית - סימן את לידתה של התיאוריה הקוונטית.

במודל ריילי-ג’ינס, האנרגיה הממוצעת המשויכת לאורך גל מסוים של גלים עומדים בחלל היא זהה עבור כל אורכי הגל והיא פרופורציונלית ל-. פלאנק השתמש באותם רעיונות קלאסיים כמו במודל ריילי-ג’ינס כדי להגיע לצפיפות האנרגיה כמכפלה של קבועים והאנרגיה הממוצעת עבור אורך גל נתון, אבל האנרגיה הממוצעת אינה נתונה על ידי משפט החלוקה השווה.

האנרגיה הממוצעת של גל היא הפרש האנרגיה הממוצע בין רמות המתנד, משוקלל על פי ההסתברות של הגל להיפלט. השקלול הזה מבוסס על התפוסה של מצבי אנרגיה גבוהה יותר כפי שמתואר על ידי חוק ההתפלגות של בולצמן. על פי חוק זה, ההסתברות של מצב להיות תפוס היא פרופורציונלית לגורם , כאשר היא האנרגיה של המצב.

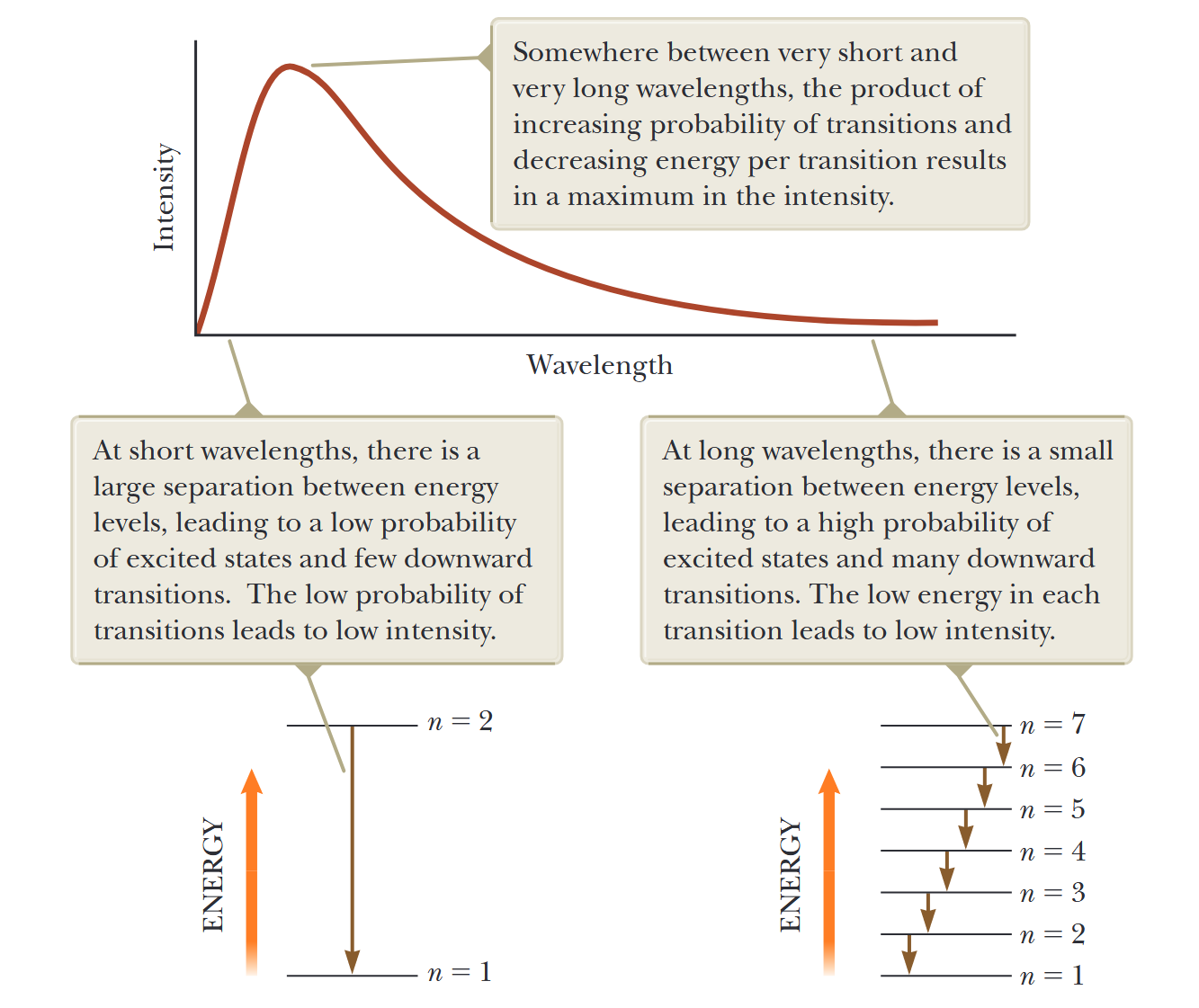
bookhue

איור 1.5: במודל של פלאנק, האנרגיה הממוצעת המשויכת לאורך גל נתון היא המכפלה של האנרגיה של מעבר וגורם הקשור להסתברות שהמעבר יתרחש.

בתדירויות נמוכות (אורכי גל ארוכים), רמות האנרגיה מופרדות על ידי פערים קטנים בגודל (משוואה (SJ39.5)) והן קרובות זו לזו כמו בצד ימין באיור 1.5. רבים ממצבי האנרגיה מעוררים כיוון שהגורם של בולצמן הוא יחסית גדול עבור מצבים אלה. לכן, יש תרומות רבות לקרינה היוצאת, אם כי כל תרומה היא בעלת אנרגיה נמוכה מאוד.

כעת, בואו נבחן קרינת תדירות גבוהה, כלומר, קרינה עם אורך גל קצר. עבור קרינה זו, במשוואה (SJ39.5) הוא גדול והאנרגיות המותרות רחוקות מאוד זו מזו כמו בצד שמאל באיור 1.5. ההסתברות של עירור תרמי לעורר את רמות האנרגיה הגבוהות האלה קטנה בגלל הערך הקטן של גורם בולצמן עבור ערכים גדולים של . בתדירויות גבוהות, ההסתברות הנמוכה של עירור מביאה לתרומה מועטה מאוד לאנרגיה הכוללת, למרות שכל קוונטום הוא בעל אנרגיה גדולה. ההסתברות הנמוכה הזו “הופכת את העקומה” ומורידה אותה לאפס שוב באורכי גל קצרים.

באמצעות גישה זו, פלאנק יצר ביטוי תיאורטי עבור התפלגות אורך הגל שהסכים באופן מדהים עם העקומות הניסיוניות באיור 1.2:

הפונקציה הזו כוללת את הפרמטר , שפלאנק התאים כך שהעקומה שלו תתאים לנתונים הניסיוניים בכל אורכי הגל. הערך של הפרמטר הזה נמצא להיות בלתי תלוי בחומר שממנו עשוי הגוף השחור ובלתי תלוי בטמפרטורה; הוא קבוע יסודי של הטבע. הערך של , קבוע פלאנק, הוא:

באורכי גל ארוכים, משוואה (SJ39.6) מצטמצמת לביטוי ריילי-ג’ינס, משוואה (SJ39.3), ובאורכי גל קצרים, היא חוזה ירידה אקספוננציאלית ב- עם ירידה באורך הגל, בהסכמה עם התוצאות הניסיוניות.

כאשר פלאנק הציג את התיאוריה שלו, רוב המדענים (כולל פלאנק עצמו!) לא חשבו שהמושג הקוונטי מציאותי. הם האמינו שזה טריק מתמטי שבמקרה חוזה את התוצאות הנכונות. לכן, פלאנק ואחרים המשיכו לחפש הסבר “רציונלי” יותר לקרינת גוף שחור. פיתוחים עוקבים, עם זאת, הראו שתיאוריה המבוססת על המושג הקוונטי (ולא על מושגים קלאסיים) הייתה צריכה לשמש כדי להסביר לא רק קרינת גוף שחור אלא גם מספר תופעות אחרות ברמה האטומית.

בשנת 1905, איינשטיין גזר מחדש את התוצאות של פלאנק על ידי הנחה שהתנודות של השדה האלקטרומגנטי עצמן מקוונטות. במילים אחרות, הוא הציע שקוונטיזציה היא תכונה יסודית של אור וקרינה אלקטרומגנטית אחרת, מה שהוביל למושג הפוטונים.

קריטי להצלחת התיאוריה הקוונטית או תיאוריית הפוטונים היה הקשר בין אנרגיה ותדירות (משוואה (SJ39.5)), שהתיאוריה הקלאסית נכשלה לחלוטין לחזות.

דוגמה: קרינה תרמית מעצמים שונים

איור 1.6: מצאו את אורך הגל בשיא של קרינת גוף שחור הנפלטת על ידי גוף האדם כאשר טמפרטורת העור היא .

פתרון:

קרינה תרמית נפלטת מפני השטח של כל עצם. אורך הגל השיא קשור לטמפרטורת השטח דרך חוק ההעתקה של וין.

נפתור את משוואה (SJ39.2) עבור :

נחליף את טמפרטורת השטח בקלווין:

קרינה זו נמצאת באזור האינפרא-אדום של הספקטרום ואינה גלויה לעין האנושית. חיות מסוימות (צפעוני בור, למשל) מסוגלות לזהות קרינה באורך גל זה ולכן יכולות לאתר טרף חם-דם אפילו בחושך.

דוגמה: המתנד המקוונט

איור 1.7: מסה של מחוברת לקפיץ חסר מסה שיש לו קבוע כוח של . הקפיץ נמתח ממצב השיווי שלו ומשוחרר ממנוחה.

מצאו את האנרגיה הכוללת של המערכת ואת תדירות התנודה על פי חישובים קלאסיים.

פתרון:

על בסיס הדרך שבה המסה מתחילה תנועה, המשרעת שלו היא .

נעריך את האנרגיה הכוללת של מערכת המסה-קפיץ:

נחשב את תדירות התנודה:

  1. בהנחה שהאנרגיה של המתנד מקוונטת, מצא את המספר הקוונטי עבור המערכת התונדת עם המשרעת הזו.

נמדל כעת את מערכת מסה-קפיץ זו כמתנד פלאנק. נפתור את (SJ39.4) עבור המספר הקוונטי :

נציב את הערכים:

נשים לב שזהו מספר עצום, שדי טיפוסי למערכות בגדלים יום-יומיים. השינוי באנרגיה בין מצב קוונטי זה למצב קוונטי כל כך זעום שלא ניתן אפילו למדוד אותו.

האפקט הפוטואלקטרי

קרינת גוף שחור הייתה התופעה הראשונה שהוסברה באמצעות מודל קוונטי. בחלק האחרון של המאה ה-19, באותו זמן שנאספו נתונים על קרינה תרמית, הניסויים הראו שאור הפוגע במשטחים מתכתיים מסוימים גורם לאלקטרונים להיפלט מאותם משטחים. תופעה זו ידועה כהאפקט הפוטואלקטרי, והאלקטרונים הנפלטים נקראים פוטואלקטרונים.

האיור הבא הוא תרשים של מכשיר לחקר האפקט הפוטואלקטרי.
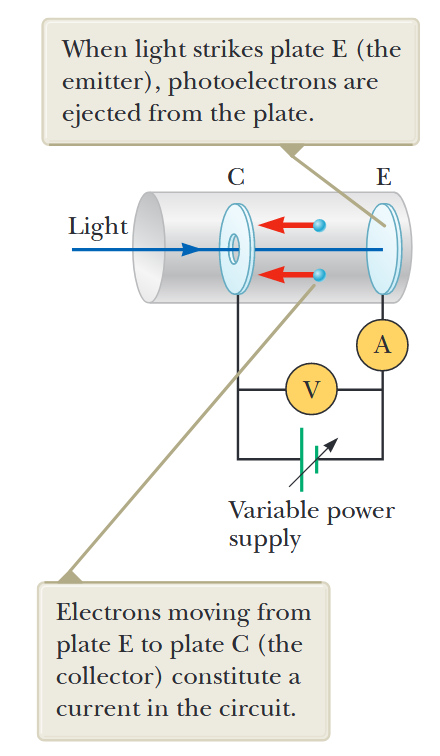
bookhue

איור 1.8: תרשים מעגל לחקר האפקט הפוטואלקטרי. כאשר אור פוגע בלוח E (הפולט), פוטואלקטרונים נפלטים מהלוח. אלקטרונים הנעים מלוח E ללוח C (הקולט) מהווים זרם במעגל. (Serway et al., 2019).

צינור זכוכית או קוורץ מכיל לוח מתכתי E (הפולט) המחובר לקוטב השלילי של סוללה ולוח מתכתי אחר C (הקולט) המחובר לקוטב החיובי של הסוללה. כאשר הצינור נשמר בחושך, המד הזרם קורא אפס, מה שמעיד על היעדר זרם במעגל. עם זאת, כאשר לוח E מואר באור בעל אורך גל מתאים, זרם מזוהה על ידי המד, מה שמעיד על זרימת מטענים על פני הרווח בין לוחות E ו-C. הזרם הזה נובע מפוטואלקטרונים הנפלטים מלוח E ונאספים בלוח C.

האיור הבא הוא גרף של זרם פוטואלקטרי כפונקציה של הפרש הפוטנציאל המופעל בין לוחות E ו-C עבור שתי עוצמות אור.

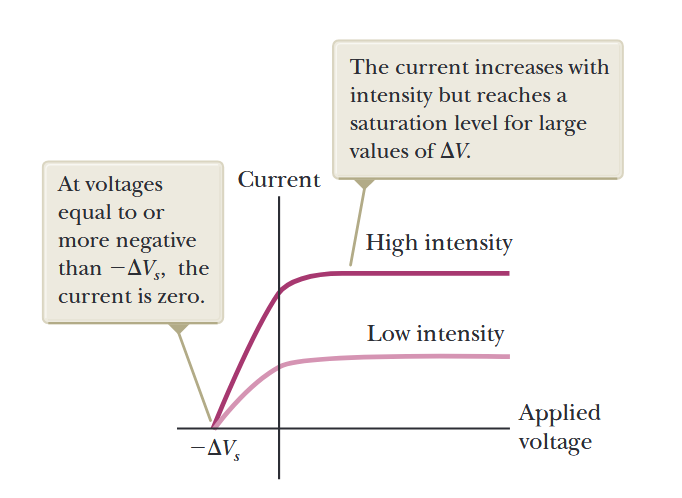
bookhue

איור 1.9: זרם פוטואלקטרי כפונקציה של הפרש פוטנציאל מופעל עבור שתי עוצמות אור. בפוטנציאלים השווים או שליליים יותר מ-, הזרם הוא אפס. הזרם עולה עם העוצמה אך מגיע לרמת רוויה עבור ערכים גדולים של V. (Serway et al., 2019).

בערכים גדולים של , הזרם מגיע לערך מקסימלי; כל האלקטרונים הנפלטים מ-E נאספים ב-C, והזרם אינו יכול לעלות עוד. בנוסף, הזרם המקסימלי עולה כאשר עוצמת האור הפוגע עולה, כפי שאפשר לצפות, מכיוון שיותר אלקטרונים נפלטים על ידי האור בעוצמה גבוהה יותר.

לבסוף, כאשר שלילי - כלומר, כאשר הסוללה במעגל הפוכה כך שלוח E חיובי ולוח C שלילי - הזרם יורד כיוון שרבים מהפוטואלקטרונים הנפלטים מ-E נדחים על ידי לוח C השלילי כעת. במצב זה, רק אותם פוטואלקטרונים בעלי האנרגיה הקינטית הגדולה מ- מגיעים ללוח C, כאשר הוא גודל המטען על האלקטרון.

כאשר שווה או שלילי יותר מ-, כש- הוא הפוטנציאל העוצר, אין פוטואלקטרונים המגיעים ל-C והזרם הוא אפס.

בואו נמדל את השילוב של השדה החשמלי בין הלוחות ואלקטרון הנפלט מלוח E כמערכת מבודדת. נניח שהאלקטרון הזה עוצר בדיוק כשהוא מגיע ללוח C. מכיוון שהמערכת מבודדת, לפי החוק הראשון של התרמודינמיקה:

כאשר התצורה הראשונית היא ברגע שהאלקטרון עוזב את המתכת עם אנרגיה קינטית והתצורה הסופית היא כאשר האלקטרון עוצר בדיוק לפני שהוא נוגע בלוח C. אם נגדיר את האנרגיה הפוטנציאלית החשמלית של המערכת בתצורה הראשונית להיות אפס, יש לנו:

כעת נניח שהפרש הפוטנציאל מוגדל בכיוון השלילי בדיוק עד שהזרם הוא אפס ב-. במקרה זה, לאלקטרון שעוצר מיד לפני שהוא מגיע ללוח C יש את האנרגיה הקינטית המקסימלית האפשרית בעת עזיבת משטח המתכת. המשוואה הקודמת יכולה להיכתב אז כ:

משוואה זו מאפשרת לנו למדוד את בניסוי על ידי קביעת גודל המתח שבו הזרם יורד לאפס.

מספר מאפיינים של האפקט הפוטואלקטרי מפורטים להלן. עבור כל מאפיין, אנו משווים את התחזיות שעשויות על ידי גישה קלאסית, תוך שימוש במודל הגל עבור אור, עם התוצאות הניסיוניות.

  1. תלות האנרגיה הקינטית של פוטואלקטרון בעוצמת האור
    תחזית קלאסית: אלקטרונים צריכים לספוג אנרגיה ברציפות מהגלים האלקטרומגנטיים. כאשר עוצמת האור הפוגע במתכת מוגברת, אנרגיה צריכה להיות מועברת למתכת בקצב גבוה יותר והאלקטרונים צריכים להיפלט עם יותר אנרגיה קינטית. על פי משוואה (SJ39.8), אם כן, הפוטנציאל העוצר צריך לעלות בגודל עם הגדלת עוצמת האור.

    תוצאה ניסיונית: האנרגיה הקינטית המקסימלית של פוטואלקטרונים אינה תלויה בעוצמת האור כפי שמוצג באיור 1.7, עם שתי העקומות יורדות לאפס באותו מתח שלילי.

  2. מרווח הזמן בין פגיעת האור לבין פליטת פוטואלקטרונים
    תחזית קלאסית: בעוצמות אור נמוכות, מרווח זמן מדיד צריך לחלוף בין הרגע שבו האור מופעל לבין הזמן שבו אלקטרון נפלט מהמתכת. מרווח זמן זה נדרש כדי שהאלקטרון יספוג את הקרינה הפוגעת לפני שהוא רוכש מספיק אנרגיה לברוח מהמתכת.

    תוצאה ניסיונית: אלקטרונים נפלטים מפני השטח של המתכת כמעט באופן מיידי (פחות מ- לאחר הארת השטח), אפילו בעוצמות אור נמוכות מאוד.

  3. תלות פליטת אלקטרונים בתדירות האור
    תחזית קלאסית: אלקטרונים צריכים להיפלט מהמתכת בכל תדירות אור פוגע, כל עוד עוצמת האור גבוהה מספיק, מכיוון שאנרגיה מועברת למתכת ללא תלות בתדירות האור הפוגע.

    תוצאה ניסיונית: אין אלקטרונים נפלטים אם תדירות האור הפוגע יורדת מתחת לתדירות חיתוך מסוימת , שערכה אופייני לחומר המואר. אין אלקטרונים נפלטים מתחת לתדירות חיתוך זו ללא תלות בעוצמת האור.

  4. תלות האנרגיה הקינטית של פוטואלקטרון בתדירות האור
    תחזית קלאסית: לא צריך להיות קשר בין תדירות האור לבין האנרגיה הקינטית של האלקטרון. האנרגיה הקינטית צריכה להיות קשורה לעוצמת האור.

    תוצאה ניסיונית: האנרגיה הקינטית המקסימלית של הפוטואלקטרונים עולה עם הגדלת תדירות האור.

עבור מאפיינים אלה, התוצאות הניסיוניות סותרות את כל ארבע התחזיות הקלאסיות.

הסבר מוצלח של האפקט הפוטואלקטרי ניתן על ידי איינשטיין בשנת 1905, באותה שנה שבה הוא פרסם את תורת היחסות הפרטית שלו. כחלק ממאמר כללי על קרינה אלקטרומגנטית, שעבורו הוא קיבל פרס נובל בפיזיקה בשנת 1921, איינשטיין הרחיב את מושג הקוונטיזציה של פלאנק לגלים אלקטרומגנטיים.

איינשטיין הניח שאור (או כל גל אלקטרומגנטי אחר) בתדירות מכל מקור ניתן לראות כזרם של קוונטות. כיום אנו קוראים לקוונטות האלה פוטונים. לכל פוטון יש אנרגיה הנתונה במשוואה (SJ39.5), , וכל אחד נע בוואקום במהירות האור , כאשר .

בואו נארגן את המודל של איינשטיין לאפקט הפוטואלקטרי באמצעות תכונות מודלים מבניים:

  1. רכיבים פיזיקליים:
    אנו מדמיינים שהמערכת מורכבת משני רכיבים פיזיקליים: (1) אלקטרון שיש לפלוט אותו על ידי פוטון נכנס ו-(2) שאר המתכת.

  2. התנהגות הרכיבים:

    • במודל של איינשטיין, פוטון של האור הפוגע נותן את כל האנרגיה שלו לאלקטרון יחיד במתכת. לכן, ספיגת האנרגיה על ידי האלקטרונים אינה תהליך רציף כפי שנראה במודל הגל, אלא תהליך לא רציף שבו אנרגיה מועברת לאלקטרונים בחבילות. העברת האנרגיה מתבצעת באמצעות אירוע פוטון-אחד/אלקטרון-אחד.

    • אנו יכולים לתאר את התפתחות הזמן של המערכת על ידי הפעלת מודל המערכת הלא מבודדת לאנרגיה על פני מרווח זמן הכולל את ספיגת פוטון אחד ואת פליטת האלקטרון המתאים. למערכת יש שני סוגי אנרגיה: האנרגיה הפוטנציאלית של מערכת המתכת-אלקטרון והאנרגיה הקינטית של האלקטרון הנפלט. לכן, אנו יכולים לכתוב את משוואת שימור האנרגיה כ:

    העברת האנרגיה למערכת היא זו של הפוטון, . במהלך התהליך, האנרגיה הקינטית של האלקטרון עולה מאפס לערכה הסופי, שאנו מניחים שהוא הערך המקסימלי האפשרי . האנרגיה הפוטנציאלית של המערכת עולה מכיוון שהאלקטרון נמשך הרחק מהמתכת אליה הוא נמשך.

    אנו מגדירים את האנרגיה הפוטנציאלית של המערכת כאשר האלקטרון נמצא מחוץ למתכת כאפס. האנרגיה הפוטנציאלית של המערכת כאשר האלקטרון במתכת היא , כאשר נקראת פונקציית העבודה של המתכת. פונקציית העבודה מייצגת את האנרגיה המינימלית שבה אלקטרון קשור במתכת והיא בסדר גודל של מספר אלקטרון וולט.

הטבלה הבאה מציגה ערכים נבחרים של פונקציות עבודה:

מתכת

בהצבת האנרגיות הללו במשוואה (SJ39.9), יש לנו:

אם האלקטרון עושה התנגשויות עם אלקטרונים אחרים או יוני מתכת כשהוא נפלט, חלק מהאנרגיה הנכנסת מועברת למתכת והאלקטרון נפלט עם פחות אנרגיה קינטית מ-.

התחזית שעשה איינשטיין היא משוואה לאנרגיה הקינטית המקסימלית של אלקטרון נפלט כפונקציה של תדירות הקרינה המאירה. משוואה זו יכולה להימצא על ידי סידור מחדש של משוואה (SJ39.10):

עם המודל המבני של איינשטיין, ניתן להסביר את המאפיינים הנצפים של האפקט הפוטואלקטרי שלא ניתן להבין באמצעות מושגים קלאסיים:

  1. תלות האנרגיה הקינטית של פוטואלקטרון בעוצמת האור
    משוואה (SJ39.11) מראה ש- אינה תלויה בעוצמת האור. האנרגיה הקינטית המקסימלית של כל אלקטרון אחד, השווה ל-, תלויה רק בתדירות האור ובפונקציית העבודה. אם עוצמת האור מוכפלת, מספר הפוטונים המגיעים ליחידת זמן מוכפל, מה שמכפיל את הקצב שבו פוטואלקטרונים נפלטים. האנרגיה הקינטית המקסימלית של כל פוטואלקטרון אחד, עם זאת, אינה משתנה.

  2. מרווח הזמן בין פגיעת האור לבין פליטת פוטואלקטרונים
    פליטה כמעט מיידית של אלקטרונים עקבית עם מודל הפוטון של אור. האנרגיה הפוגעת מופיעה בחבילות קטנות, ויש אינטראקציה אחד-לאחד בין פוטונים ואלקטרונים. אם לאור הפוגע יש עוצמה נמוכה מאוד, יש מעט מאוד פוטונים המגיעים ליחידת זמן; כל פוטון, עם זאת, יכול להיות בעל אנרגיה מספקת לפלוט אלקטרון מיידית.

  3. תלות פליטת אלקטרונים בתדירות האור
    מכיוון שהפוטון חייב להיות בעל אנרגיה גדולה יותר מפונקציית העבודה כדי לפלוט אלקטרון, לא ניתן לצפות באפקט הפוטואלקטרי מתחת לתדירות חיתוך מסוימת. אם האנרגיה של פוטון נכנס אינה עומדת בדרישה זו, לא ניתן לפלוט אלקטרון מהשטח, למרות שפוטונים רבים ליחידת זמן פוגעים במתכת בקרן אור עזה מאוד.

  4. תלות האנרגיה הקינטית של פוטואלקטרון בתדירות האור
    פוטון בתדירות גבוהה יותר נושא יותר אנרגיה ולכן פולט פוטואלקטרון עם יותר אנרגיה קינטית מאשר פוטון בתדירות נמוכה יותר כפי שמתואר במשוואה (SJ39.11).

המודל של איינשטיין חוזה קשר לינארי (משוואה (SJ39.11)) בין האנרגיה הקינטית המקסימלית של האלקטרון לבין תדירות האור . תצפית ניסיונית של קשר לינארי בין ו- תהיה אישור סופי של תיאוריית איינשטיין. אכן, קשר לינארי כזה נצפה בניסוי תוך כמה שנים מתיאוריית איינשטיין והוא מתואר באיור הבא.
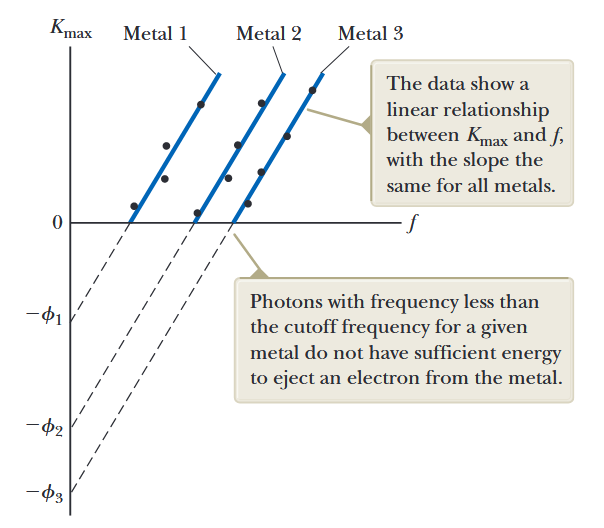
bookhue

איור 1.10: גרף של עבור פוטואלקטרונים כפונקציה של תדירות האור הפוגע בניסוי אפקט פוטואלקטרי טיפוסי. הנתונים מראים קשר לינארי בין ו-, עם השיפוע זהה עבור כל המתכות. לפוטונים עם תדירות קטנה יותר מתדירות החיתוך עבור מתכת נתונה אין אנרגיה מספקת לפלוט אלקטרון מהמתכת. (Serway et al., 2019).

השיפוע של הקווים בגרף כזה הוא קבוע פלאנק . החיתוך על הציר האופקי נותן את תדירות החיתוך מתחתיה אין פוטואלקטרונים נפלטים. על ידי הצבת במשוואה (SJ39.11), אנו קובעים שתדירות החיתוך קשורה לפונקציית העבודה דרך הקשר .

תדירות החיתוך מתאימה לאורך גל חיתוך , כאשר:

ו- הוא מהירות האור. אורכי גל גדולים מ- הפוגעים בחומר בעל פונקציית עבודה אינם מביאים לפליטת פוטואלקטרונים.

השילוב במשוואה (SJ39.12) מופיע לעתים קרובות כאשר מקשרים את האנרגיה של פוטון לאורך הגל שלו. קיצור נפוץ בפתרון בעיות הוא לבטא שילוב זה ביחידות שימושיות על פי הקירוב הבא:

או

Å

אפקט קומפטון

בשנת 1919, איינשטיין הסיק שפוטון בעל אנרגיה נוסע בכיוון יחיד ונושא תנע . בשנת 1923, ארתור הולי קומפטון (1892–1962) ופיטר דביי (1884–1966) המשיכו באופן עצמאי את הרעיון של איינשטיין על תנע פוטון הלאה.

לפני 1922, קומפטון ועמיתיו לעבודה צברו ראיות המראות שהתיאוריה הקלאסית הגלית של האור נכשלה להסביר את פיזור קרני רנטגן מאלקטרונים. על פי התיאוריה הקלאסית, גלים אלקטרומגנטיים בתדירות הפוגעים באלקטרונים צריכים להיות בעלי שתי השפעות:

  1. לחץ קרינה צריך לגרום לאלקטרונים להאיץ בכיוון התפשטות הגלים.
  2. השדה החשמלי התונד של הקרינה הפוגעת צריך להכניס את האלקטרונים לתנודה בתדירות הנראית , כאשר היא התדירות במסגרת ייחוס של האלקטרונים הנעים.

התדירות הנראית הזו שונה מהתדירות של הקרינה הפוגעת בגלל אפקט דופלר. כל אלקטרון תחילה בולע קרינה כחלקיק נע ואז מקרין מחדש כחלקיק נע, ובכך מפגין שתי הסטות דופלר בתדירות הקרינה. מכיוון שאלקטרונים שונים נעים במהירויות שונות לאחר האינטראקציה, בהתאם לכמות האנרגיה הנבלעת מהגלים האלקטרומגנטיים, תדירות הגל המפוזר בזווית נתונה לקרינה הנכנסת צריכה להראות התפלגות של ערכים מוסטים על ידי דופלר.

בניגוד לתחזית זו, הניסויים של קומפטון הראו שבזווית נתונה נצפית רק תדירות אחת של קרינה. איך אנו מסבירים את אי ההסכמה הזו בין תיאוריה לניסוי?

קומפטון ועמיתיו לעבודה הסבירו תוצאות אלה על ידי התייחסות לפוטונים לא כגלים אלא כחלקיקים דמויי נקודה בעלי אנרגיה ותנע ועל ידי הנחה שהאנרגיה והתנע של המערכת המבודדת של זוג הפוטון-אלקטרון המתנגש נשמרים. קומפטון אימץ מודל חלקיק עבור משהו שהיה ידוע היטב כגל, וכיום תופעת הפיזור הזו ידועה כאפקט קומפטון.

האיור הבא מראה את התמונה הקוונטית של ההתנגשות בין פוטון רנטגן בודד בתדירות לבין אלקטרון.

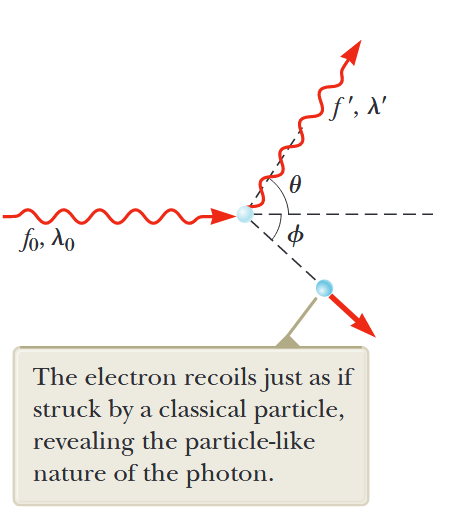
bookhue

איור 1.11: המודל הקוונטי לפיזור קרני רנטגן מאלקטרון. האלקטרון נפלט בזווית ביחס לכיוון זה כמו בהתנגשות דמוית כדורי ביליארד. (Serway et al., 2019).

במודל הקוונטי, האלקטרון מתפזר דרך זווית ביחס לכיוון זה כמו בהתנגשות דמוית כדורי ביליארד. (הסמל המשמש כאן הוא זווית ואין לבלבל אותו עם פונקציית העבודה, שנדונה בסעיף הקודם.)

האיור הבא הוא תרשים סכמטי של המכשיר שבו השתמש קומפטון.

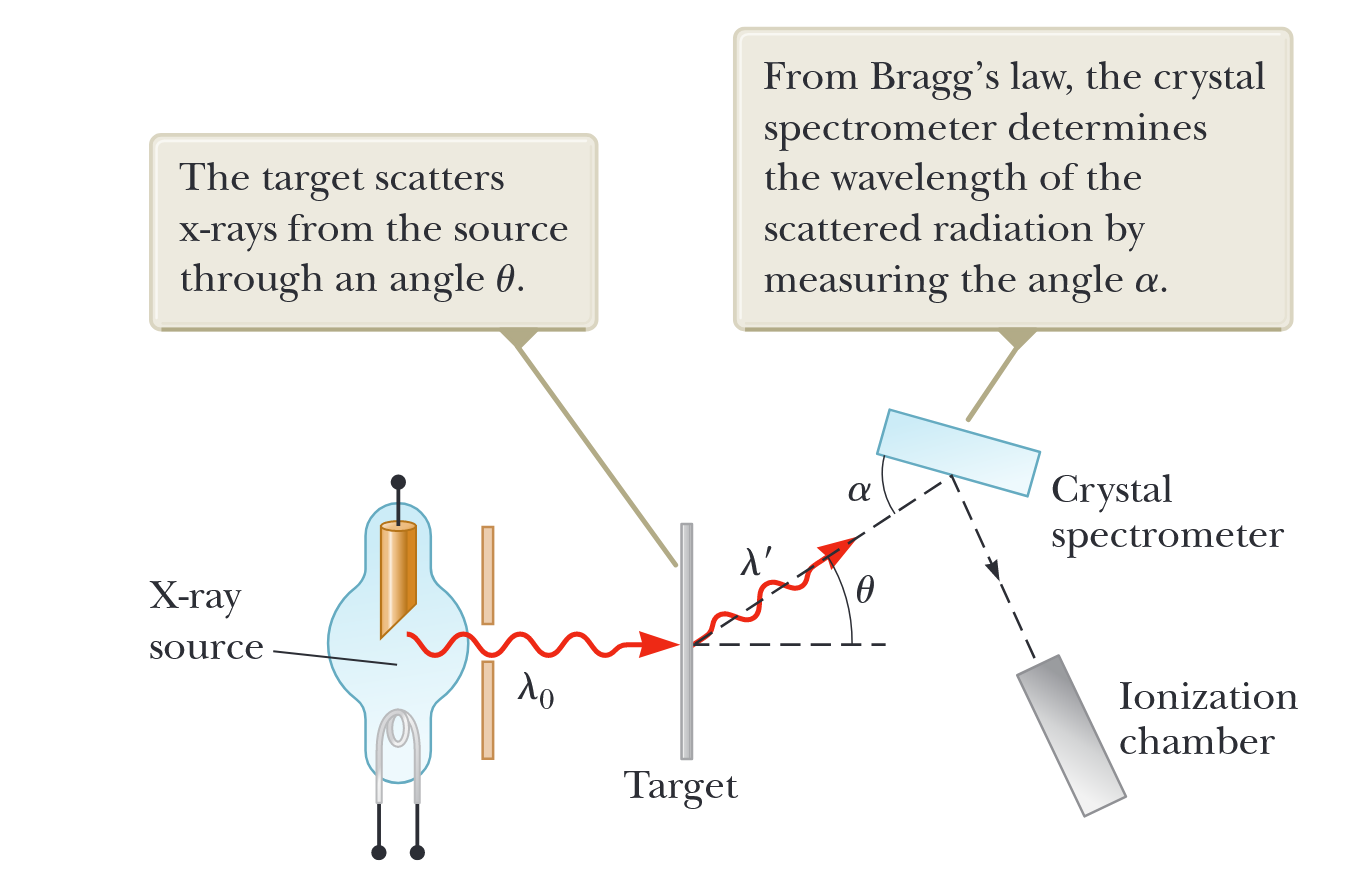
bookhue

תרשים סכמטי של מכשיר קומפטון. (Serway et al., 2019).

קרני הרנטגן, המפוזרות ממטרת פחמן, עברו דיפרקציה על ידי ספקטרומטר גבישי מסתובב, והעוצמה נמדדה עם תא יינון שיצר זרם פרופורציונלי לעוצמה. הקרן הפוגעת הורכבה מקרני רנטגן מונוכרומטיות באורך גל .

הגרפים הניסיוניים של עוצמה כפונקציה של אורך גל שנצפו על ידי קומפטון עבור ארבע זוויות פיזור מוצגים באיור הבא.

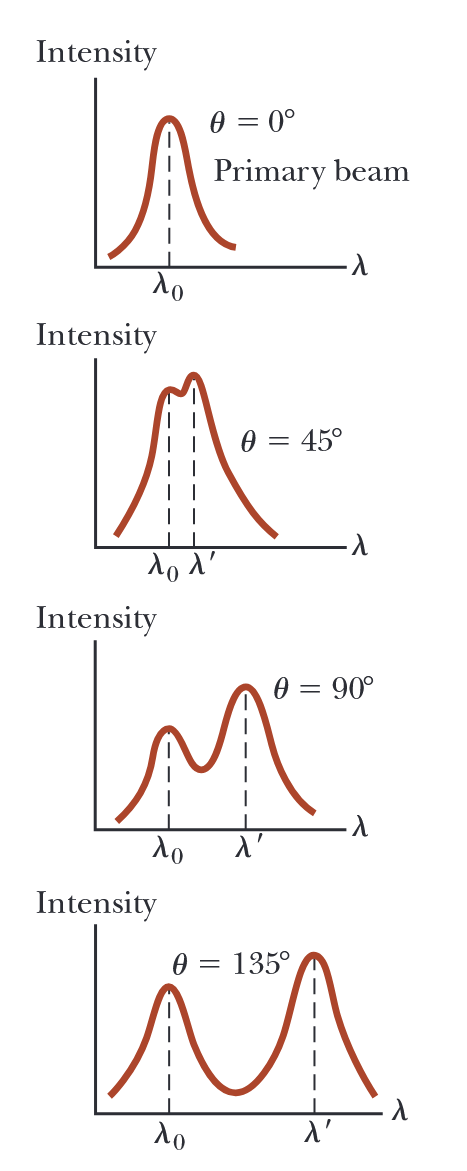
bookhue

עוצמת קרני רנטגן מפוזרות כפונקציה של אורך גל עבור פיזור קומפטון ב-. (Serway et al., 2019).

הגרפים עבור שלוש הזוויות הלא-אפסיות מראים שני שיאים, אחד ב- ואחד ב-. השיא המוסט ב- נגרם על ידי פיזור קרני רנטגן מאלקטרונים חופשיים, אשר חזה קומפטון שתלוי בזווית הפיזור כ:

כאשר הוא מסת האלקטרון. ביטוי זה ידוע כמשוואת ההסטה של קומפטון ומתאר נכון את המיקומים של השיאים באיור 1.11.

הגורם , הנקרא אורך הגל של קומפטון של האלקטרון, בעל ערך מקובל כיום של:

אנו יכולים להיעזר בטיעון אנרגטי כדי לראות מדוע אורך הגל של הפוטון עולה בפיזור קומפטון.
אנרגיה מועברת מהפוטון הנכנס לאלקטרון בתהליך. מכיוון ש-, תדירות הפוטון המפוזר יורדת, ומכיוון ש-, אורך הגל שלו עולה. כאשר זווית הפיזור עולה, יותר אנרגיה מועברת מהפוטון הפוגע לאלקטרון. כתוצאה מכך, האנרגיה של הפוטון המפוזר יורדת עם הגדלת זווית הפיזור.

השיא הלא-מוסט ב- באיור 1.11 נגרם על ידי קרני רנטגן המפוזרות מאלקטרונים הקשורים חזק לאטומי המטרה. השיא הלא-מוסט הזה גם חזוי על ידי משוואה (SJ39.13) אם מסת האלקטרון מוחלפת במסה של אטום פחמן, שהיא בערך פעמים מסת האלקטרון. לכן, יש הסטת אורך גל עבור פיזור מאלקטרון הקשור לאטום, אבל היא כל כך קטנה שלא הייתה ניתנת לזיהוי בניסוי של קומפטון.

המדידות של קומפטון היו בהסכמה מעולה עם התחזיות של משוואה (SJ39.13). כעת ראינו שלושה ניסויים הדורשים הסבר קוונטי כדי להביא תיאוריה להסכמה עם התוצאות הניסיוניות. התוצאות של ניסוי קומפטון היו הראשונות לשכנע פיזיקאים רבים בתקפות היסודית של התיאוריה הקוונטית.

דוגמה: פיזור קומפטון ב-45°

קרני רנטגן באורך גל מתפזרות ממסה מסוימת. קרני הרנטגן המפוזרות נצפות בזווית של לקרן הפוגעת. חשבו את אורך הגל שלהן.

פתרון:

נפתור את משוואה (SJ39.13) עבור אורך הגל של קרן הרנטגן המפוזרת:

נציב ערכים מספריים:

טבעם של גלים אלקטרומגנטיים

תופעות כמו האפקט הפוטואלקטרי ואפקט קומפטון מציעות ראיות חד-משמעיות שכאשר אור (או צורות אחרות של קרינה אלקטרומגנטית) וחומר מקיימים אינטראקציה, האור מתנהג כאילו הוא מורכב מחלקיקים בעלי אנרגיה ותנע .

איך יכול אור להיחשב פוטון (במילים אחרות, חלקיק) כאשר אנחנו יודעים שהוא גל? מצד אחד, אנו מתארים אור במונחים של פוטונים בעלי אנרגיה ותנע. מצד שני, אור וגלים אלקטרומגנטיים אחרים מפגינים השפעות הפרעה ודיפרקציה, כפי שראינו בפיזיקה 2, שעקביות רק עם פרשנות גלית.

איזה מודל נכון? האם אור הוא גל או חלקיק? התשובה תלויה בתופעה הנצפית. ניסויים מסוימים יכולים להיות מוסברים טוב יותר או אך ורק עם מודל הפוטון, ואילו אחרים מוסברים טוב יותר או אך ורק עם מודל הגל.

עלינו לקבל את שני המודלים ולהודות שהטבע האמיתי של האור אינו ניתן לתיאור במונחים של כל תמונה קלאסית יחידה. אותה קרן אור שיכולה לפלוט פוטואלקטרונים ממתכת (כלומר, שהקרן מורכבת מפוטונים) יכולה גם להיות מופרקת על ידי סורג (כלומר, שהקרן היא גל). במילים אחרות, מודל החלקיק ומודל הגל של אור משלימים זה את זה.

הצלחת מודל החלקיק של אור בהסבר האפקט הפוטואלקטרי ואפקט קומפטון מעלה שאלות רבות אחרות. אם אור הוא חלקיק, מה המשמעות של “התדירות” ו”אורך הגל” של החלקיק? האם אור הוא בו-זמנית גל וחלקיק? למרות שלפוטונים אין אנרגיית מנוחה (כמות לא ניתנת לצפייה מכיוון שפוטון לא יכול להיות במנוחה), האם יש ביטוי פשוט למסה האפקטיבית של פוטון נע? אם לפוטונים יש מסה אפקטיבית, האם הם חווים משיכה כבידתית? מה הוא הטווח המרחבי של פוטון, ואיך אלקטרון בולע או מפזר פוטון אחד?

חלק מהשאלות הללו ניתנות למענה, אבל אחרות דורשות השקפה על תהליכים אטומיים שהיא ציורית ומילולית מדי. רבות מהן נובעות מאנלוגיות קלאסיות כמו כדורי ביליארד מתנגשים וגלי אוקיינוס נשברים על חוף הים.

מכניקת הקוונטים נותנת לאור טבע גמיש יותר על ידי התייחסות למודל החלקיק ולמודל הגל של אור כשניהם הכרחיים ומשלימים. אף מודל לא יכול לשמש באופן בלעדי לתיאור כל התכונות של האור. הבנה מלאה של ההתנהגות הנצפית של האור יכולה להיות מושגת רק אם שני המודלים משולבים באופן משלים.

עמודים המציינים את העמוד הזה